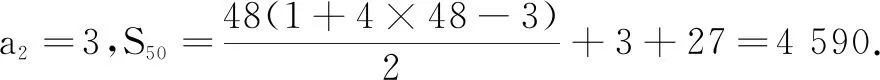强化知识联系 加深本质理解
——以“数列”教学为例
2022-07-13刘雪明
刘雪明
(北京市房山区教师进修学校,102401)
数列是一类特殊的函数,是数学重要的研究对象,也是研究其他类型函数的基本工具,在日常生活中有着广泛的应用.《普遍高中数学课程标准》(2017年版)提出:“感受数列与函数的共性与差异,体会数学的整体性”,“感悟数列是可以用来刻画现实世界中一类具有递推规律事物的数学模型”[1].这就提醒我们,在学习数列的过程中,要善于激活自身已有知识和学习经验,建立新旧知识之间的关联,在区别与联系中加深对数列本质的理解.
一、数列与函数的联系
“数列是一类特殊的函数”包含两层含义,一方面数列是函数,我们可以类比函数的学习路径来学习数列,用研究函数的方法来研究数列问题.另一方面,同一般函数相比,数列又具有特殊性,特殊在数列是离散的,其定义域是正整数集或其有限子集,数列的表示方法除了列表法、图象法、解析式法外,还有一种是递推公式法.数列是可以用来刻画现实世界中一类具有递推规律事物的数学模型.由函数f(x)可以生成数列{an},其中an=f(n),点(n,an)是函数f(x)图象上的离散的点.可以说,数列是函数的局部,函数f(x)具有的性质,数列{an}一般都具有,但数列{an}具有的某些性质,函数f(x)不一定具有.
例1(多选题)已知数列{an}是各项均为正数的等比数列,{bn}是公差不为0的等差数列,且a2=b2,a8=b8.则下列选项中成立的有( )
(A)a5=b5(B)a5 (C)a4 分析2联想数列与函数的关系,公差不为0的等差数列的通项公式是关于n的一次函数形式,其图象是一条直线上的离散的点.等比数列的通项公式是关于n的指数函数形式,其图象是相应的指数函数图象上的离散的点.两个图象在n=2,n=8处相交,联想一次函数和指数函数的图象与性质,不论它们递增还是递减,都有an 点评通过作差法比较大小是常规方法,容易想到,但是计算量大、变形技巧性强,令很多同学望而生畏,无从下手.如果从函数的角度来思考,借助一次函数和指数函数的图象与性质,数列{an}与{bn}中的项与项的大小关系一目了然,简捷直观.在解决数列问题时,要牢记数列是一类特殊的函数,要善于从函数的视角去思考和处理数列问题.如将数列的最大项转化为函数的最大值,单调(或周期)数列转化为单调(或周期)函数,通项的取值范围转化为函数的值域等.把函数概念、图象、性质有机地融入数列中,通过数列与函数知识的相互联系,不断优化和完善知识网络,不断发展与提高思维能力. 例2设数列{an}的通项公式为an=n2+λn,若{an}单调递增,求实数λ的取值范围. 解法1因为{an}单调递增,所以an 通过数列与函数的比较,既可以从函数观点、连续与离散关系的角度认识数列,突出数列的本质,又可以从离散现象认识连续现象,深化对函数的理解,丰富函数的内涵,更有利于从函数角度去考虑数列问题,拓宽解题思路,提升数学素养. 数列是按照一定顺序排列的一列数,一般表示为{an}.虽然用类似集合的符号{an}表示数列,但数列不是集合,因为数列的项与项之间排列有序,且项的值可以重复出现,而集合中的元素具有互异性和无序性,即一个元素在一个集合中只能出现一次,一个集合中的两个元素可以任意交换位置而集合不变. 例3(北京市房山区2021年测试题)设集合A={x|x=4n-3,n∈N*},B={x|x=3n-1,n∈N*}, 把集合A∪B中的元素按从小到大依次排列,构成数列{an},则a2=______,数列{an}的前50项和S50=______. 点评此题以集合为背景,考查数列的概念、等差数列的通项公式与前n项和公式、等比数列的通项公式.深刻理解集合元素的互异性、无序性和数列的有序性、项的可重复性是正确解题的关键,从函数角度认识数列也是简化解题过程的关键. 例4(江苏省南通市2019届高三第二次调研测试题)已知集合A={x|x=2k-1,k∈N*},B={x|x=8k-8,k∈N*},从集合A中取出m个不同元素,其和记为S;从集合B中取出n个不同元素,其和记为T.若S+T≤967,则m+2n的最大值为______. 点评本题以集合为背景,考查数列的概念、等差数列的前n项和公式,又涉及基本不等式、最值问题,巧妙地将不同知识点有机整合,较好地考查数学知识与解题能力.此题还可以利用三角函数、解析几何的知识进行解决. 通过以上分析,我们可以切实感受到数列与集合、数列与函数等知识间的联系与区别,解决这些问题可以进一步加深我们对相关知识的理解.数学知识是一个系统,具有逻辑性和整体性的特点,数学中联系是普遍存在的,所以我们要注重知识之间的联系,加强数学内部的纵向联系、不同学科间的横向联系,学会用联系的观点学习数学,加深对数学本质的理解,体会数学的整体性.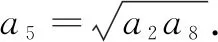

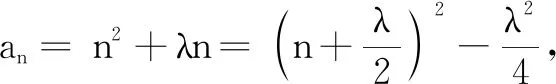

二、数列与集合的联系