着眼数学运算 提升核心素养——以“数列运算”教学为例

刘荣坤

(福建省福安市第一中学，355000)

数学运算不仅是学生的六大数学核心素养之一,而且是培养学生各种关键能力的基础．运算能力的高低直接影响学生解决数学问题的进程,是学生学好数学的最核心的要求．因此在教学中,发展学生的数学运算素养,保证运算的准确性、灵活性、合理性、简捷性就尤为重要．本文以数列运算教学为例试加阐释．

一、正确辨识概念,保证运算的准确性

数学概念揭示了数学对象的本质属性,是数学运算法则导出的逻辑基础,是逐步形成运算技能、发展运算素养的基石[1]．数列这一章的概念不多,以等差数列和等比数列为主,若只是死记概念,没有深刻理解“等差”、“等比”的内涵,那么在复杂的计算中就容易发生错误．

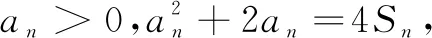
例3在数列{an}中,a1=1,an+1=2an+2n,求通项公式an.

二、合理运用性质,提高运算的灵活性

代数的本质是运算,代数性质总是与运算相关,“运算中的规律性,运算中的不变性”是代数性质的研究主题[2]．因此在解题过程中总是离不开利用数学对象的性质．

例4已知等差数列{an}满足Sp=q,Sq=p,求Sp+q(p≠q).

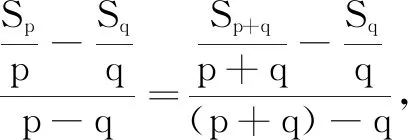
我们提倡通性通法,但如果学生能够在熟练掌握算理、运算法则和运算方法的前提下,还能灵活应用数学性质进行运算,就能提高运算的灵活性．在实际教学过程中,要对“数学性质”有一个宏观性的认识,引领学生亲身经历性质的获得过程(比如，如何将等差数列的性质类比到等比数列的性质),提高类比、归纳等能力,获得“四基”,提高“四能”．并在此基础上提出具有数学含金量的运算问题,熟练利用性质进行解答,提高运算的灵活性,从而激发学生的创造性思维,发展数学运算的核心素养．

三、把握合情推理,寻找运算的合理性

探究式教学是提高学生独立思考与探索发现能力的重要教学途径[3]．合情推理具有猜测和发现结论的作用,能够为探求运算思路提供方向的作用．将探究式教学和合情推理结合起来,能培养学生的数学精神,启迪思维,有助于学生核心素养的提升．在数列这一章中有很多内容可以设计探究性课程,可以设计以下的问题串进行探究.

问题1你见过类似的问题吗?你是怎么解决的?

这是已知递推关系式求通项公式,此时按照低起点的原则提出:

问题2在数列{an}中,a1=1,an+1=2an+1,求通项公式an.

从特殊情况入手寻找规律,由已知得:a1=1,a2=3,a3=7,a4=15,a5=31,然后将每一项都加上一个1,就会构成一个等比数列,即a1+1=21,a2+1=22,a3+1=23,a4+1=24,a5+1=25，…，an+1=2n．虽然是不完全归纳,但我们发现{an+1}是等比数列,可以将an+1=2an+1的两边同时加上1得an+1+1=2an+2=2(an+1),所以{an+1}是等比数列．并由其引申出当递推公式为an+1=kan+b时,如何求通项公式(构造等比数列)．

问题3在数列{an}中,a1=1,an+1=2an+n,求通项公式an.

可以启发学生类比问题2的构造法进行求解,但是构造的数列必须是bn=an+xn+y,因为该例条件中是n,所以构造的必须是一次函数的形式．

问题4在数列{an}中,a1=1,a2=1,an+2=an+1+an,求通项公式an.

启发学生是不是也可以转化为一个等比数列bn+1=tbn?此时bn应该是什么形式?应是bn=xan+1+yan的形式,所以可设xan+2+yan+1=t(xan+1+yan),实际上可以简化成an+2+san+1=t(an+1+san)这种形式．这就构造了一个等比数列,问题得到圆满解决．

合情推理的主要表现形式为类比和归纳,虽说其不可靠,但却可为探究运算思路提供方向,使得运算过程更真实、自然、更合理、更符合学生的思维特征．

四、运用数学思想,提升运算的简捷性

新的课程标准在课程结构中将函数单独作为一个主题.数列是特殊的函数,所以在学习数列时就可以用函数来类比,将学习函数的经验迁移到数列的学习中来,领会其中所蕴含的数学思想方法．比如等差数列的前n项和Sn可以看成特殊的二次函数,那么例4就产生了如下想法:不妨令Sp=ap2+bp=q,Sq=aq2+bq=p,两式相减得a(p2-q2)+b(p-q)=q-p,即a(p+q)+b=-1,所以Sp+q=a(p+q)2+b(p+q)=(p+q)[a(p+q)+b]=-(p+q)．

数学思想是数学的灵魂[5].在数学运算过程中,运算对象的转化,运算方向的探求,运算方法的选择，数学思想方法都起着不可忽视的作用．上述解法中,前者用到整体代换和换元的思想,后者从函数的观点来认识数列,使得运算更加简捷．因此,在数列的运算教学中,应通过例题和习题不断渗透类比、化归、转化等数学思想,正确迁移函数中的处理方法,准确应用法则．学生明晰了算理,在运算过程中自觉使用数学思想方法,就会使运算更简捷,这将有助于提高学生的运算素养．