旋转作用下无磁耗散的磁Rayleigh-Bénard问题的稳定性

邵慧敏，刘蒙蒙，宋方应

(福州大学数学与统计学院，福建 福州 350108)

0 引言

考虑水平夹板中处在重力场下的静止流体，其下层比上层热. 当上下层的温差相对于流体黏性及热导系数适当大时，该静止状态将会不稳定，即对该状态进行微小扰动，则扰动会进一步放大. 特别地，下层轻的热流体向上运动，上层重的冷流体向下运动，形成热对流现象. 目前热对流不稳定性问题(也称Rayleigh-Bénard问题)已被广泛研究，本研究主要讨论磁流体中的热对流问题.

1951年，Thompson[1]首次研究外加磁场对磁流体中热不稳定性的影响. 后来Chandr-asekhar[2]理论上发现磁场具有抑制热不稳定性的作用. 该理论结果被Nakagawa[3]在物理实验上验证. 1985年，Galdi[4]则通过有磁耗散的磁Boussinesq方程数学上严格验证了该抑制现象. 最近，Jiang等[5]进一步给出无磁耗散情形的数学证明. 本研究则在文献[5]的研究基础上进一步考虑旋转下的无磁耗散的磁Rayleigh-Bénard问题，其中数学模型如下：

(1)

下面简要介绍上述模型中的数学符号.

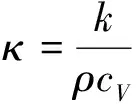
由于考虑上述模型的解是水平周期运动的，因此引入如下有限高且水平方向上是周期的区域：Ωh:={(xh,x3)∈R3|xh:=(x1,x2)∈T, 00，2πL2>0是水平两个方向的周期长度.该区域的边界记为∂Ωh:=T×{0,h}.

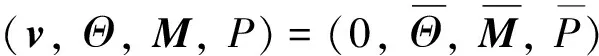
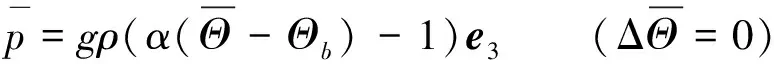
(2)

现在，沿式(1)的平衡态进行微扰，则有如下扰动量表示：

则扰动量(v,θ,N,β)满足如下扰动方程组:

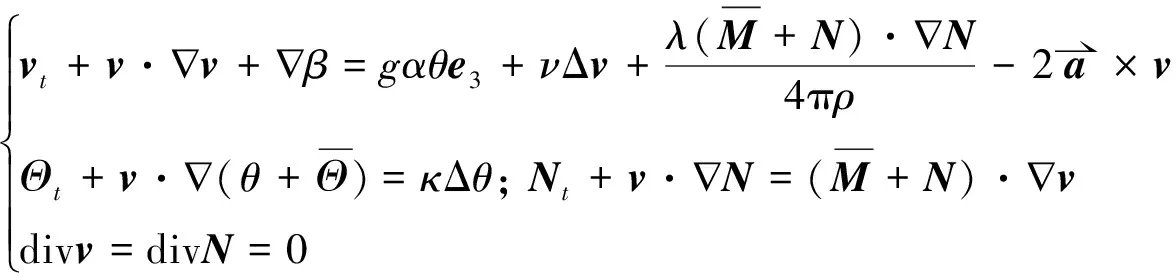
(3)

给予如下初边值条件：

(v,θ,N)cct=0=(v0,θ0,N0)， (v,θ)|∂Ωh=0

(4)

结果，旋转下磁Rayleigh-Bénard问题的稳定性问题可归结为初边值问题(3)～(4)是否存在稳定性解.

1 拉格朗日坐标变换

由于直接研究初边值问题(3)～(4)的稳定性是很困难的，将该问题转化到拉格朗日坐标系下. 为此，定义可逆映射ζ0:=ζ0(y):Ωh→Ωh，其满足∂Ωh=ζ0(∂Ωh)，det∇ζ0=1.并定义流映射ζ为初始值问题ζt(y,t)=v(ζ(y,t),t)和ζ(y, 0)=ζ0的解.

(5)

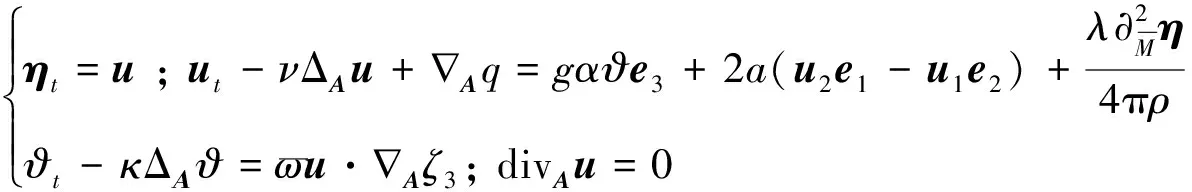
(6)

(7)

(η, ϑ,u)|t=0=(η0, ϑ0,u0)，(η, ϑ,u)|∂Ω=0

(8)

结果，初边值问题(3)～(4)是否存在稳定性解可归结为变换磁Rayleigh-Bénard问题(7)～(8)是否存在稳定性解.

2 主要结果

主要建立起变换磁Rayleigh-Bénard问题(7)～(8)的稳定性条件，并在该条件下给出变换磁Rayleigh-Bénard问题(7)～(8)存在稳定性解. 在给出主要结果之前，需要介绍一些简化符号.

现在给出本研究的主要结果.

2)ζ0:=y+η0满足∂Ωh=ζ0(∂Ωh)和det∇ζ0=1;

(9)

注2由于稳定性条件与角速度a无关，因此定理1的结果表明旋转应该不具有促进磁流体中的热不稳定性产生的作用.

注3当δ>0充分小时，有ζ:=η+y:Ω→Ω是微分同胚映射，因此可通过无量纲处理的逆过程，以及拉格朗日坐标逆变换得到初边值问题(3)～(4)的稳定性解，且该解关于时间代数衰减.

3 定理1的证明

类似于文[6]中的线性迭代方法，很容易建立起变换磁Rayleigh-Bénard问题(7)～(8) 的关于时间局部解存在性结果，因此为了得到定理1的全局存在性结果及稳定性估计(9)，只需建立起先验稳定性估计(9)即可. 为此，令(η,u, ϑ)及q为问题(7)～(8)的古典解，并且对于任意给定的T>0，满足：

(10)

det(I+∇η0)=1

(11)

其中，δ是充分小的，只依赖于已知的物理参数. 则通过类似于文[5]的标准能量方法，很容易得到下列低阶、高阶和最高阶能量不等式.

(12)

(13)

(14)

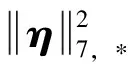
结果可知：

(15)

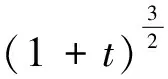
从而

(16)

对式(13)的t进行积分，可得：

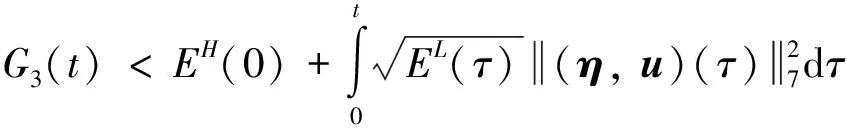
(17)

(18)

则可从式(16)～(17)推出：

从而

(19)

(20)