接种和迁移的多斑块传染病模型生存性分析

黄裕淞，魏凤英

(福州大学数学与统计学院，福建 福州 350108)

0 引言

传染病在某个区域传播后，会随着人群的流动在不同区域开始传播. 研究多斑块传染病模型的动力学特征十分必要，相关研究成果较为丰富. 例如利用非负矩阵的相关理论，结合图论构造 Lyapunov 函数，进而探讨传染病模型的动力学行为[1-4]； 采用随机过程刻画传染病模型的主要参数，讨论多斑块传染病模型的灭绝与持久性生存问题[5-8].

疫苗接种后，人体获得的免疫能力并非长久有效，因此，一些学者提出了临时免疫并开展研究[9-12]. 结合个体迁移方面的研究工作[13-14]，假定接种人群在不同斑块之间的流动不受限制，提出具有接种和迁移的SIV多斑块模型：

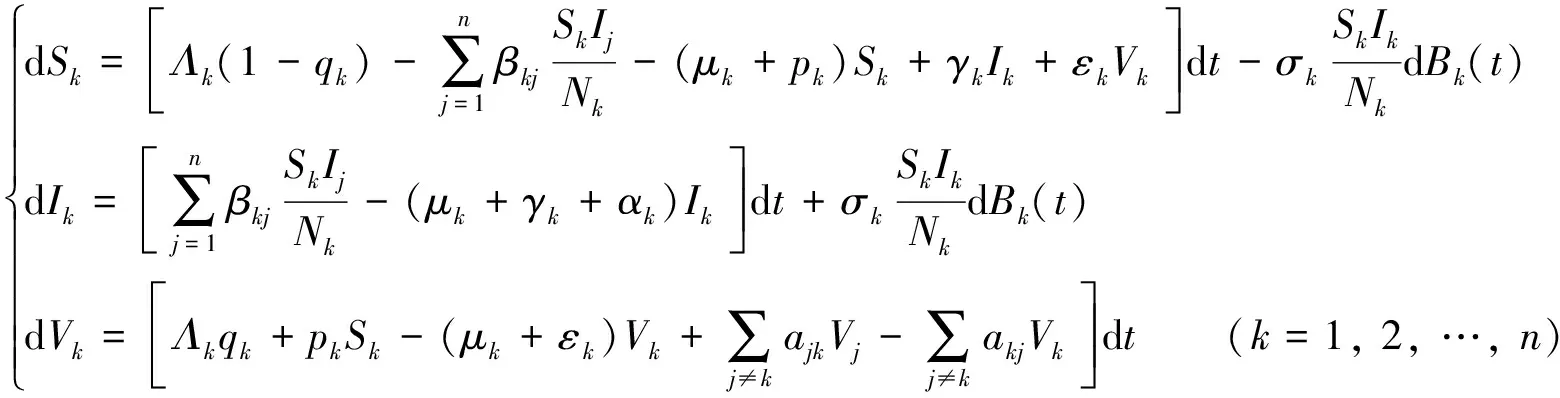
(1)

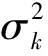
1 解的存在唯一性

定理1的证明参照文献[15]的定理1，此处略去.

证明 对于模型(1)，求出：

(2)

类似地，得到：

(3)

2 平稳的马尔可夫过程

定理2假设(βkj)n×n是不可约的.若R0>1，且

(4)

(5)

(ω1,ω2, …,ωn)ρ(M0)=(ω1,ω2, …,ωn)M0

(6)

定义一个C2函数F:Γ→R，即：

F(S1,I1,V1; …;Sn,In,Vn)=NW1+W2+W3+W4+W5

(7)

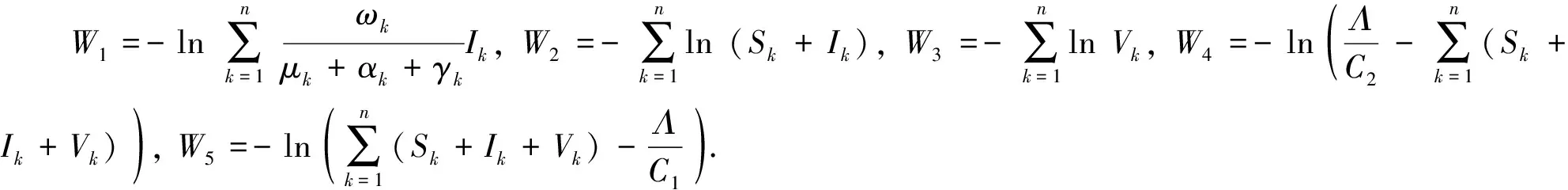
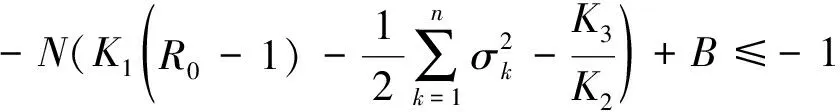
(8)

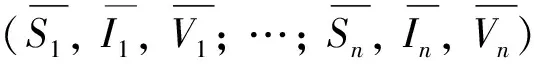
下面，定义一个C2函数W:Γ→R+∪{0}，即：W(S1,I1,V1; …;Sn,In,Vn)=NW1+W2+W3+W4+

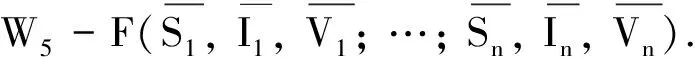
类似地，可得：

(10)

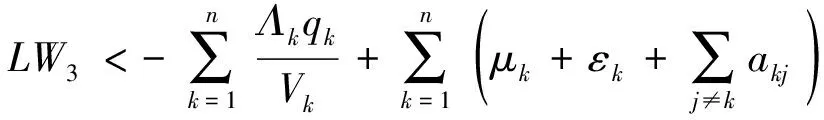
(11)

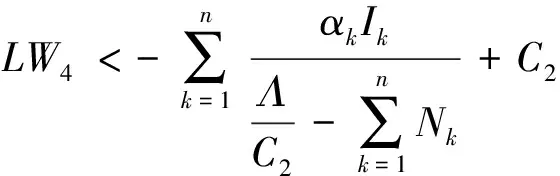
(12)

(13)

于是有：

(14)

其中:

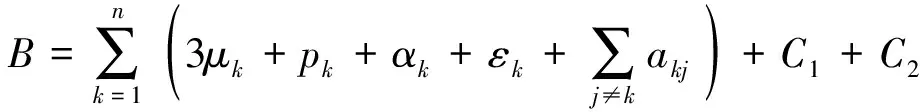
(15)

定义有界闭集Uε如下：

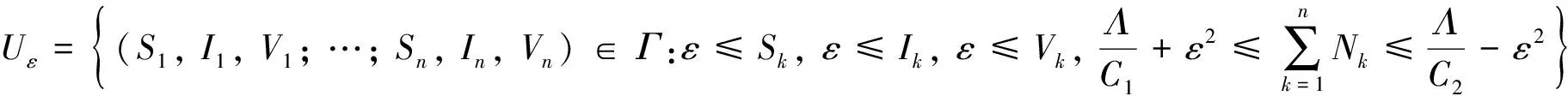
(16)

k=1, 2, …,n.其中ε>0是一个充分小的常数.在集合ΓUε中，通过选择足够小的ε满足：

(17)

为了验证LW≤-1在ΓUε中总是成立的，把ΓUε分成4个部分：

(18)

情况1当(S1,I1,V1; …;Sn,In,Vn)∈U3时，有：

(19)

情况2当(S1,I1,V1; …;Sn,In,Vn)∈U4时，则有：

(20)

所以，LW≤-1在ΓUε总成立，证毕.

3 感染者的灭绝性

定理3若

(21)

则每个斑块的感染者数量都趋于零，K1见(5)式.

(22)

其中：

则有：

(24)

对不等式(24)两边同时积分并除于t，可得到：

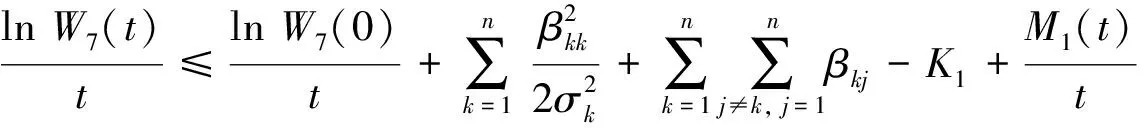
(25)

其中：

(26)

上式是一个局部鞅，其二次变分为：

(27)

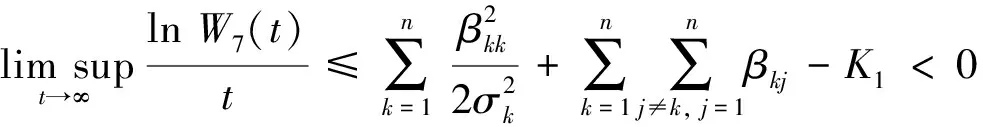
(28)

定理4假设(βkj)n×n是不可约的.若

(29)

则每个斑块的感染者数量都趋于零，其中K1和K2见式(5).

其中：

(31)

于是有:

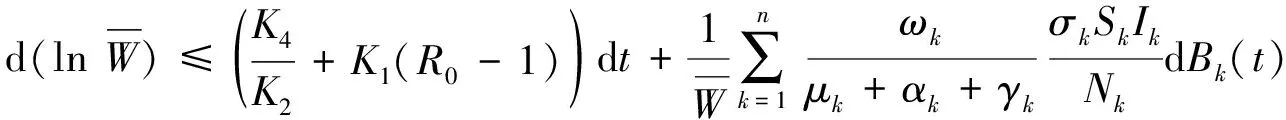
(32)

对式(32)两边积分并除于t，有：

(33)

这里

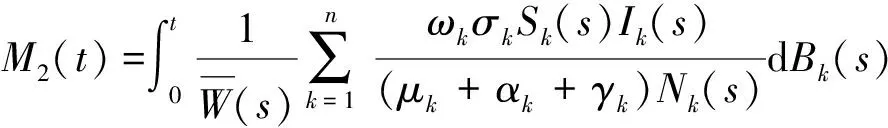
(34)

上式是一个局部鞅，其二次变分为：

(35)

(36)

4 数值模拟

图1 模型(1)的感染者数量的模拟路径 Fig.1 Paths of the number of the infected to model(1)

下面验证定理2的充分条件.当β11=0.57,β12=0.5,β21=0.45,β22=0.5时，有：R0=2.959 3>1, 且

(37)

定理2的条件满足，那么模型(1)存在平稳分布，疾病将流行，如图1～2所示.

(a) S1的直方图

(b) I1的直方图

(c) V1的直方图

(d) S2的直方图

(e) I2的直方图

(f) V2的直方图

图3 感染者灭绝性的模拟路径Fig.3 Paths of the extinction of the infected

最后，验证灭绝性的充分条件. 取β11=0.045,β12=0.03,β21=0.03,β22=0.045时，得到：

(38)

定理3和定理4的条件都满足，因此疾病将会灭绝，如图3所示.

5 结语

本研究讨论了具有接种和迁移的多斑块SIV传染病模型(1). 首先证明了模型(1)的正解在任意正初值下的全局存在唯一性； 接着通过多组Lyapunov函数的构造，证明了模型(1)存在平稳的马尔可夫过程(见定理2). 通过验证灭绝性的充分条件，得到感染者数量将趋于灭绝的结论(见定理3～4)，最后应用数值模拟验证了主要结果．