求解一般l1趋势过滤问题的原始对偶内点法
2022-07-13张体琪刘勇进
张体琪,刘勇进
(福州大学数学与统计学院,福建 福州 350108)
0 引言
对于给定的噪声信号y=(y1, …,yn)∈n和正整数k, 一般l1趋势过滤问题具有以下的形式:

(1)

D(k, n)=D(1, n-k+1)D(k-1, n)(k≥2)
其中D(1, p)∈(p-1)×p为p上的一阶差分矩阵.
非参数回归是一个热门的研究领域,学者们已经提出了众多的方法. 趋势过滤是一种重要的非参数回归模型,它是一种带惩罚项的最小二乘拟合优化方法. 趋势过滤的应用非常广泛,包括宏观经济学[1]、社会科学[2]、金融时间序列分析[3]、收益管理[4]、地球物理学[5]、噪声处理[6-7]等领域. 为了解决一些实际的经济问题,许多具有线性时间复杂度的趋势过滤方法已经被提出,比如,指数平滑方法[8]、平均滤波方法[9]和Hodrick-Prescott(H-P)滤波方法[10]. Kim等[11]在2009年提出了l1趋势过滤方法,它基于H-P滤波方法做了一些变化,即用绝对值的和(l1范数)代替H-P滤波方法中用于惩罚估计趋势变化的平方和(l2范数).但他们只解决了k=2的情况,因此,将这种思想推广到更一般的情况,提出一种能够解决一般l1趋势过滤问题(k≥2)的原始对偶内点法.
本研究针对一般l1趋势过滤问题提出一种原始对偶内点法.首先,介绍一些相关的预备知识,分析原始对偶内点法中求解迭代方向的过程,进而给出算法的迭代框架.然后,给出原始对偶内点法的收敛性分析以及算法复杂度分析.最后,在合成数据集和真实数据集上进行相关的实验,展示原始对偶内点法与半光滑牛顿增广拉格朗日方法、交替方向乘子法解决一般l1趋势过滤问题的数值对比结果.实验结果表明, 对于不同的调节参数λ和k阶差分矩阵,原始对偶内点法都具有较好的性能.
1 原始对偶内点法
原始对偶内点法是目前求解二次规划或其他凸优化规划问题最有效的求解方法之一. 该方法是Gonzalez-Lima等[12]求解线性规划问题时,利用原始对偶方法产生的一个线性系统的简化. 这种简化的主要特征是它在解集上有定义并且保持了稀疏性,这些特性增加了算法的鲁棒性、稳定性和效率.
首先给出一些预备知识. 先将原问题(1)重构为下面的等价形式
s.t.D(k, n)x-z=0
(2)
原问题(2)的拉格朗日函数为

其中,v∈n-k为对偶变量. 原问题(2)的KKT最优化条件为
原问题(2)的对偶问题为
s.t.-λ1≤v≤λ1
(3)

D(k, n)D(k, n)Tv-D(k, n)y+μ1-μ2=0,v-λ1≤0, -v-λ1≤0
〈μ1,v-λ1〉=0, 〈μ2, -v-λ1〉=0 (μi≥0,i=1, 2, …,n)
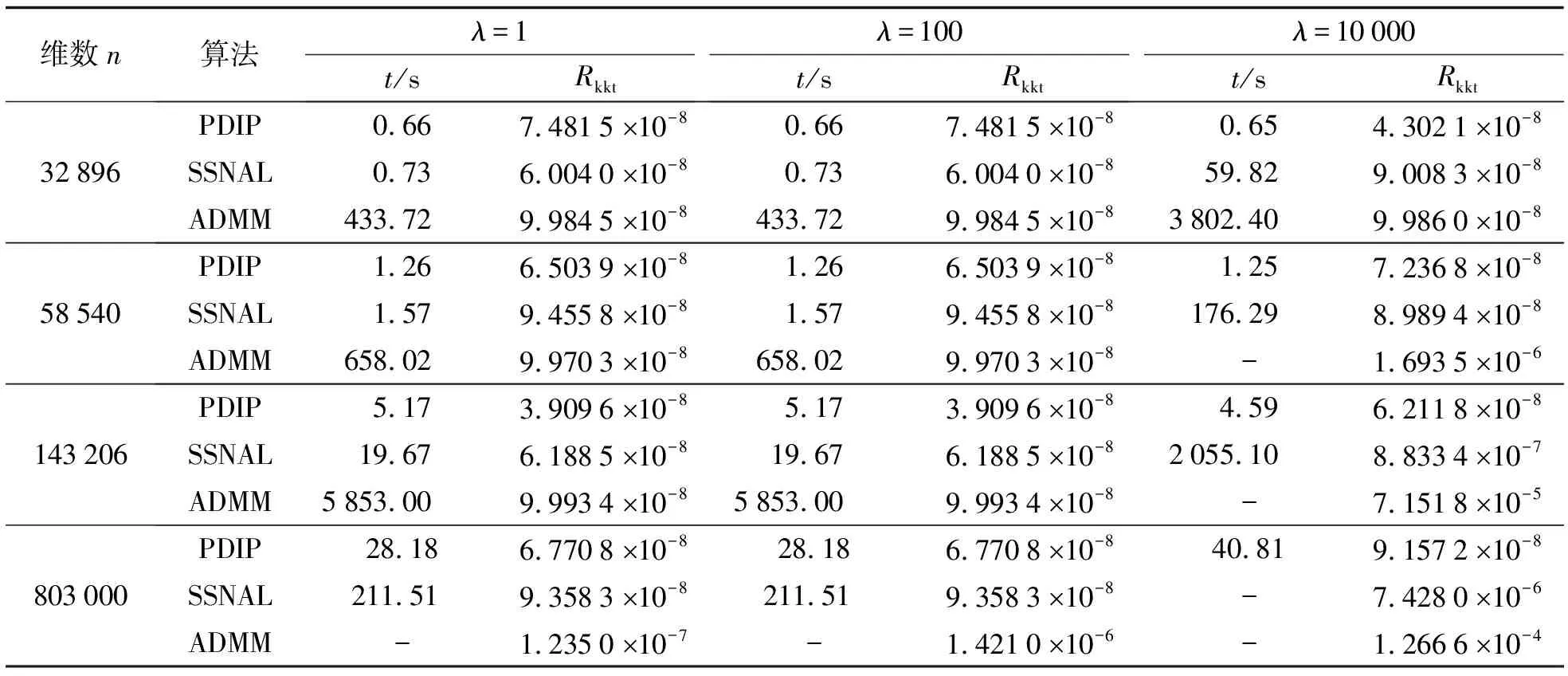
对偶问题(3)是一个关于对偶变量v的二次规划(QP)问题,如果有-λ1 本节给出原始对偶内点法中求解迭代方向的具体过程[11],为了推导方便,本节将D(k, n)全部记为D.定义如下关于残差的非线性系统.即 (4) 其中:f1v=v-λ1;f2v=-v-λ1; 扰动参数t>0; diag(x)表示对角元素为x的对角矩阵;rt(v,μ1,μ2)表示残差;0表示零矩阵.当t→∞时,rt(v,μ1,μ2)→0退化为对偶问题(3)的KKT最优化条件. rt(v+Δv,μ1+Δμ1,μ2+Δμ2)≈rt(v,μ1,μ2)+Drt(v,μ1,μ2)(Δv, Δμ1, Δμ2)T=0 其中:Drt为rt的雅可比矩阵.再进一步将此牛顿方程改写为以下的形式 Drt(v,μ1,μ2)(Δv, Δμ1, Δμ2)T=-rt(v,μ1,μ2) (5) 方程中的Δμ1和Δμ2可以由如下的等式来计算 最后,将得到的非线性系统(4)的牛顿步Δw=(Δv, Δμ1, Δμ2)作为原始对偶内点法所寻找的迭代方向. 明确了牛顿迭代方向的求解过程后,下面给出原始对偶内点法的算法迭代框架. 算法1: 原始对偶内点法(PDIP)输入: t>0, η∈(0, 0.5], ξ∈(0, 1), (v0, μ01, μ02)∈Ω, j=01. 计算非线性系统 rt(vj, μj1, μj2)=0的牛顿步(Δvj, Δμj1, Δμj2)2. 令αj=ξmj, 其中mj为满足下面不等式的最小非负整数m, 使得: rt(vj+ξmΔvj, μj1+ξmΔμj1, μj2+ξmΔμj2)≤(1-ηξm)rt(vj, μj1, μj2)(6)且(vj+ξmΔvj, μj1+ξmΔμj1, μj2+ξmΔμj2)∈Ω成立. 3. 更新 vj+1=vj+αjΔvj, μj+11=μj1+αjΔμj1, μj+12=μj2+αjΔμj24. 令j=j+1, 返回步骤1. 原始对偶内点法具有全局收敛性和局部收敛性且收敛速度为二阶收敛,其算法复杂度为O(k2n). 首先给出一些结论: 根据文献[13]的节10.2.4知道,结论2)成立等价于证明下面的性质. 性质1对任意给定的正整数k,n, 矩阵D(k, n)D(k, n)T正定. 证明 矩阵D(k, n)D(k, n)T正定等价于证明D(k, n)Tx=0只有零解,使用数学归纳法来证明D(k, n)Tx=0只有零解. 当k取值为2时,易知矩阵D(2, n)T为列满秩矩阵,故齐次线性方程组D(2, n)Tx=0只有零解. 假设取值为k时结论成立,下面证明当k+1时结论也成立,即证明齐次线性方程组 D(k+1, n)Tu=D(k, n)TD(1, n-k)Tu=0 (7) 只有零解. 由于取值为k时结论成立,即D(k, n)T列满秩,根据式(7)得到D(1, n-k)Tu=0.由于D(1, n-k)T列满秩,说明齐次方程组D(1, n-k)Tu=0只有零解,因此齐次方程组D(k+1, n)Tu=0只有零解.证毕. 性质2对任意w∈Ω, 0≤α≤min{1,αmax}, Δw为在w处的牛顿方向,有下面的不等式成立. (8) 此性质的证明在文献[13]中的节10.3.3有详细的证明,故此处略去证明过程. (9) 这说明α=1满足回溯线搜索停止条件(6),故算法最后的步长为1. 接下来给出算法的收敛性定理. 证明 当j充分大时,αj=1, 有wj+1=wj+Δwj.对最优解w*有rt(w*)=0, 可以得到 故算法二次收敛. 证毕. 在合成数据集和真实数据集上分别进行数值实验. 将原始对偶内点法与半光滑牛顿增广拉格朗日方法、交替方向乘子法进行对比,以进一步说明原始对偶内点法在解决一般l1趋势过滤问题的较好性能. 所有的数值测试都在MATLAB-R2019a中进行,运行环境为Dell台式电脑(Intel(R) Core(TM) i5-8500 CPU @3.0 GHZ,8 GB RAM). 半光滑牛顿增广拉格朗日方法是统计优化中一类重要的方法,可以应用于解决一些大规模的统计问题,包括Lasso问题[14]、SLBoxLSR问题[15]、OSCAR问题和SLOPE 问题[16]. 下面简要介绍求解一般l1趋势过滤问题的半光滑牛顿增广拉格朗日方法. 对一个闭且正常凸的函数f:→(-∞, ∞]及一个常数γ>0,γf的临近映射[17]具有如下的形式: 给定κ>0,1范数的临近映射,也被称为软阈值算子,具有以下的形式: 其中sign表示符号函数,1n表示分量全为1的n维向量.给定σ>0,定义原问题(2)的增广拉格朗日函数为 接下来给出半光滑牛顿增广拉格朗日法的算法框架. 算法2: 半光滑牛顿增广拉格朗日方法(SSNAL)输入: σ0>0, λ≥0, (x0, z0; v0)∈n×n-k×n-k, j=0.1. 计算: xj+1=argminx∈n{Φj(x):=infz Lσj(x, z; vj)}(10)2. 计算:zj+1=proxσ-1jλ·1(D(k, n)xj+1+σ-1jvj)3. 计算:vj+1=vj+σj(D(k, n)xj+1-zj+1)4. 更新σj+1↑σ∞≤+∞, 令j=j+1, 返回步骤1. (11) 交替方向乘子法也是求解凸优化问题的一种重要的方法,由Gabay等[18]在1976年首次提出. 交替方向乘子法求解一般l1趋势过滤问题的算法框架如下: 算法3: 交替方向乘子法(ADMM)输入: ω∈0, 1+52(), σ>0, (x0, z0;v0)∈n×n-k×n-k, j=0.1. 计算:xj+1∈argminx∈n Lσ(x, zj; vj)(12)2. 计算:zj+1∈argminz∈n-k Lσ(xj+1, z; vj)(13)3. 计算:vj+1=vj+ωσ(D(k, n)xj+1-zj+1)4. 令j=j+1, 返回步骤1. 求解子问题(12)可以转化为求解下面的等价形式 (In+σD(k, n)D(k, n)T)xj+1=y+D(k, n)T(σzj-vj) (14) 可以进一步应用共轭梯度法或者Cholesky分解法来得到线性系统(14)的解. 同时注意到子问题(13)具有闭式解,其形式如下: 由于求解一般l1趋势过滤问题的交替方向乘子法的关键也在于子问题(12)的求解,根据其等价形式(14),D(k, n)D(k, n)T的计算成本为O(n(n-k)2),故求解子问题(12)的等价形式(14)所需的总时间复杂度为O(n3). 使用基于原问题(2)的KKT条件的相对残差来测量所有算法获得的近似最优解的精度. 在合成数据集上对比原始对偶内点法和半光滑牛顿增广拉格朗日法、交替方向乘子法解决一般l1趋势过滤问题的数值结果,下面简要介绍合成数据集的构造过程. yt=xt+zt,t=1, …,n;xt+1=xt+vt,t=1, …,n-1 其中:vt为趋势斜率;xt为“真实”的潜在趋势;zt表示不规则分量或噪声.初始条件为x1=0, 噪声zt服从独立同分布N(0,β2).趋势斜率vt从一个简单的马尔可夫过程中选取得到.当概率为p的时候,有vt+1=vt, 即潜在趋势没有斜率变化.当概率为1-p时,从均匀分布[-b,b]上选取vt+1.同样地,从均匀分布[-b,b]上选取初始斜率v1.在实验中,设置p=0.01,β=1,b=0.5.选取参数λ=1, 100, 10 000;k=2, 4; 数据维数n=i×105,i=1, …, 5.设定算法的最长运行时间为3 h,即10 800 s. 表格中黑色横线表示算法在该参数下所用时间超出设定的最长运行时间10 800 s. 由于篇幅有限,本文只展示k=4的结果. 表1展示了当k=4、tol=1×10-7时, PDIP、SSNAL、ADMM算法在合成数据集上解决一般l1趋势过滤问题的数值对比结果,可以看到PDIP算法不管是在运行时间还是在求解精度上都仍然保持着明显的优势,并且参数λ取得越大,PDIP算法的优势更明显. 随着λ逐渐增大,SSNAL和ADMM算法已经达不到求解的精度并且还需要更长的运行时间. 故总结出:PDIP算法相比于SSNAL和ADMM算法在合成数据集上解决一般l1趋势过滤问题时更加高效和稳健. 表1 当k=4、 tol=1×10-7时,PDIP、SSNAL、ADMM算法在合成数据集上的实验结果 在真实数据集上比较PDIP和SSNAL、ADMM算法解决一般l1趋势过滤问题的数值结果. 真实数据来自PJM数据库. 在PJM数据库中选取了4个数据集作为实验的测试集. 实验选取调节参数λ=1, 100, 10 000. 数据的维数依赖于所选取的数据集的大小. 表2给出测试数据集的介绍. 表3展示了当k=4、tol=1×10-7时PDIP、SSNAL、ADMM算法在真实数据集上解决一般l1趋势过滤问题的数值结果. 表2 测试数据集介绍 表3 当k=4、 tol=1×10-7时,PDIP、SSNAL、ADMM算法在真实数据集上的实验结果 通过表3数据结果可以看出,PDIP算法的优势依旧明显. 在λ=10 000,n=803 000时, PDIP算法仍具有出色的性能表现,仅仅花费约40.81 s就求解到了满足精度的解; 但SSNAL和ADMM算法的性能表现比较差,不仅求解精度不高而且求解时间也很长. 因此可以得出结论:PDIP算法在真实数据集上解决一般l1趋势过滤问题时的性能表现明显优于SSNAL和ADMM算法的性能表现. 为求解一般l1趋势过滤问题,提出一种原始对偶内点法,给出原始对偶内点法的算法框架并对算法进行收敛性分析和时间复杂度分析,最后在合成数据集和真实数据集上进行数值实验,通过将原始对偶内点法与半光滑牛顿增广拉格朗日方法和交替方向乘子法比较,进一步证明原始对偶内点法的高效性和稳健性.1.1 迭代方向的求解
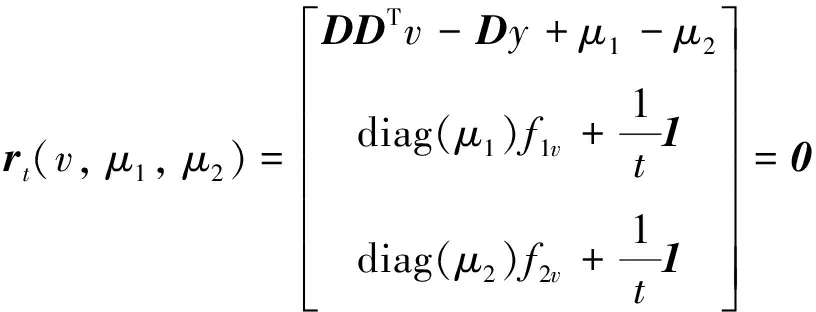
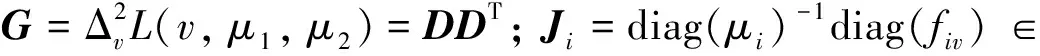

1.2 原始对偶内点法的算法框架

1.3 算法的收敛性和复杂度分析







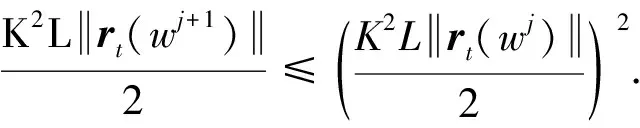


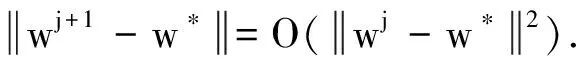
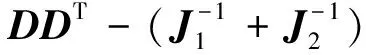
2 数值实验与结果分析
2.1 半光滑牛顿增广拉格朗日方法与交替方向乘子法
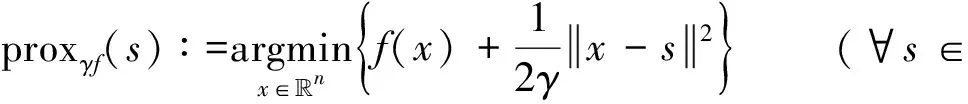
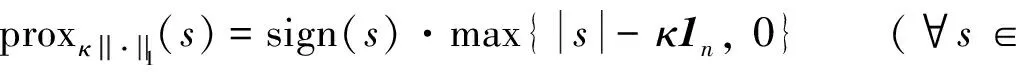





2.2 停止条件
2.3 在合成数据集上的实验结果

2.4 在真实数据集上的实验结果

3 结语
