树冠尺寸与建筑高度对街谷通风与污染物扩散的影响

张 震，黄远东，崔鹏义，刘宇辰，罗杨

（上海理工大学 环境与建筑学院，上海 200093）

街道峡谷通常指沿着两侧连续排列的建筑物之间相对狭窄的街道[1]，由于汽车尾气排放和有限的环境通风，街道峡谷成为城市大气环境中污染严重的区域[2]。迄今为止，已有研究通过数值模拟、风洞实验等手段对街道峡谷内通风及污染物扩散情况进行了详细的探讨，结果表明，影响街道峡谷内通风与污染物扩散的因素很多。例如，街道峡谷高宽比[3-5]、建筑布局[6-7]、建筑高度[8-9]、架空结构[10-12]、壁面热[13-15]及屋顶形状等[16-18]。

在城市发展更新过程中，以高楼代替低矮建筑是城市建设的主要措施，因此，在城市地区普遍存在着街道峡谷的非对称结构，其对城市大气环境的影响不容忽视[19]，很多学者也对此展开了大量的研究。Li等[20]在建筑高度对街谷内污染物分布影响的研究中发现，在升阶式街谷中，逆风建筑变高导致了街谷内污染情况的恶化。另外，当降阶式街谷中的迎风建筑物升高时，污染物浓度仅在较小风速下增加。Reiminger等[21]进一步研究了降阶式街谷内逆风建筑高度与街谷宽度变化的影响，结果表明，街谷内气流结构受建筑高度和街谷宽度的影响显著。然而以往这些研究主要针对街谷长宽比、建筑长度比、建筑高度比等方面进行探讨，降阶式结构和街道绿化特征的结合并没有得到太多的关注。树木绿化是城市街道的重要元素，其对街道峡谷内自然通风与污染物扩散有着重要的影响。Buccolieri等[22]在研究中发现，与无树木情况相比，有树木时街谷背风壁附近的污染物浓度较大，迎风壁附近的污染物浓度稍低。同时在低风速下，树木对污染物浓度的影响比在高风速下更显著。而树木种植密度和树冠孔隙度对污染物浓度的影响较小。另有研究引入空气交换率ACH对树干高度不同的街道峡谷内的通风性能进行了评估，发现当树木增加到一定高度时，ACH会随之增大[23]。尽管关于树木绿化对街谷内污染物扩散的影响研究已相当广泛，但绝大部分是围绕对称结构街谷展开，未对非对称街谷进行详细的研究，同时也很少考虑树木树冠尺寸变化的影响。

本文利用经风洞实验验证的CFD 数值模型，研究树冠尺寸与建筑高度变化对降阶式街道峡谷内自然通风与污染物扩散的影响。研究结果能从有利于街道峡谷内通风与污染物扩散的角度出发，为城市街道绿化的修剪提供一定理论指导。

1 研究方法

1.1 物理模型

如表1 所示，考虑4 种上、下游建筑高度比HA/HB=1，2，3，1.5及3种不同树冠尺寸（3×4（小型），6×8（中型），9×12（大型）），采用1∶100 的缩尺比建立以树冠、建筑、线源为主要元素的3D 降阶式街道峡谷模型（图1（以HA/HB=2 的街谷为例）），共计12 种工况。如图1（a）—1（c）所示，其中，建筑参考高度H=0.24 m（实际尺寸为24 m），街谷宽度W=H，街谷长度L=7.5H，街谷地面设置4 条具有相同源强度的平行线源，以恒定速率连续释放CO 气体，以模拟四车道道路上的交通排放。每条线源的宽度和高度均为0.021H（0.05 m），长度超出街谷末端0.92H（0.22 m）（以考虑街道交叉口的污染物排放）[24]。树冠沿街谷y轴线延伸，距地面高均为0.167H（0.04 m），大中型树冠距离两侧建筑壁面距离为0.042H（0.01 m），而小型树冠则为0.167H。

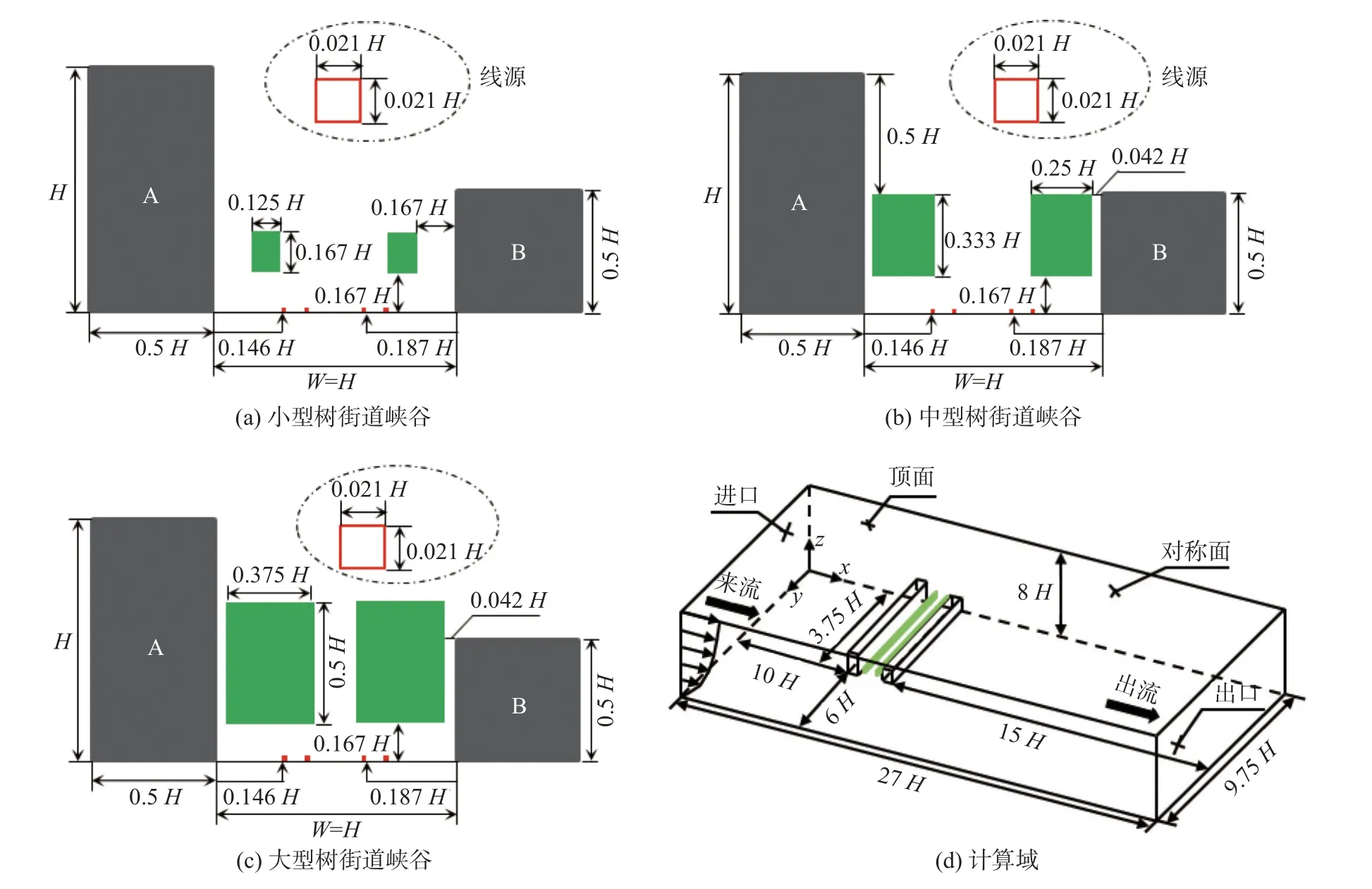
图1 街道峡谷模型Fig.1 Street canyon model

表1 物理模型参数设置Tab.1 Parameter settings of physical model

1.2 数值模型

1.2.1 控制方程

降阶式街谷内的三维稳态流动采用标准k-ε模型与标准壁函数进行求解，控制方程为[25]

式中：Cα为污染物 α的浓度；Dα,m为污染物 α在混合物中的分子扩散系数；Sα,p为污染物 α的源项；S ct为湍流施密特数（取0.7）。

采用ANSYS Fluent 14.5 软件进行数值计算，其中，控制方程应用有限体积法（FVM）离散求解，压力和速度耦合采用SIMPLE 算法与二阶迎风格式，各变量收敛残差设置为1 × 10-6。

1.2.2 树冠模型

利用Fluent 多孔介质条件对树冠进行建模[22]，通过在标准流体流动方程中添加动量源项来实现树冠的模拟。源项由两部分组成：黏性损失项与惯性损失项，具体如式（6）所示。

式中：Si为动量方程的源项；|v|为流体速度；vj为x，y，z方向速度分量；Di j与Cij为速度矩阵；ρ为空气密度。

1.2.3 计算域与网格

计算域采用对称域，图1（d）为计算域示意图，入口边界采用速度入口条件（velocity inlet），距离上游建筑迎风面10H，基于式（7）～（9），速度幂律分布u(z)、湍流动能k和湍流耗散率 ε应用于入口边界[26]；出口边界（采用outflow 条件）与下游建筑背风面距离为15H；上边界（采用symmetry 条件）距离建筑顶部7H，建筑壁面及地面均设置为壁面无滑移的边界条件（wall）。

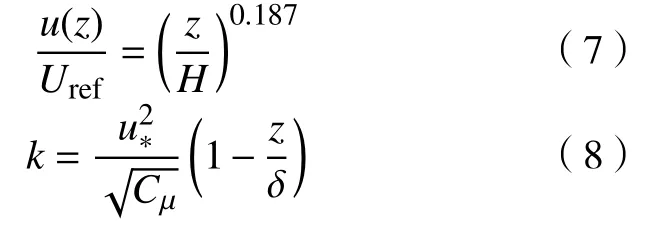
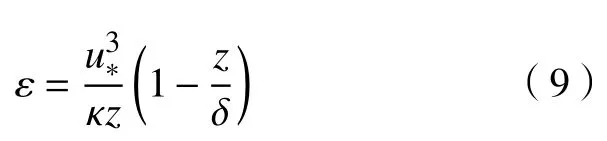
式中：u(z)为z高度的平均水平速度；Uref为建筑参考高度H处的平均水平速度，本文Uref=1.5 m/s；基于建筑高度H=0.24 m 的参考雷诺数(Re=大小为2.3×104，满足雷诺数独立；u*为摩擦速度，u*=0.54 m/s；δ为边界层厚度，δ=0.5 m；κ为卡门常数，κ=0.4。

使用六面体网格对计算域进行离散（图2）。在0.5H高度以下的街道峡内部创建大小相等的网格单元，其中，各网格单元在x，y，z轴向上的长度分别为δx=0.021H，δy=0.042H，δz=0.021H。对于0.5H高度以上，1.5H高度以下的街谷内部区域，x与y方向上的网格单元尺寸不变（δx=0.021H，δy=0.042H），z方向上2 个连续网格单元之间采用1.04 的膨胀比。对于远离街道峡谷的网格，其中，x轴向上2 个连续网格单元之间的膨胀比采用1.03，y与z轴向上的膨胀比均为1.05。研究的网格总数量为216 万。

图2 网格划分Fig.2 Mesh generation

1.3 模型验证

采用德国Karlsruhe 大学的风洞实验数据对本文模型进行验证[27]。CFD 模型采用了Karlsruhe 风洞实验的有关条件[28-29]，应用标准k-ε模型进行数值计算。图3 显示了双排植树情况下，街道峡谷背风墙和迎风墙y/H=0，1.26，3.38 这3 个不同位置处对应垂直线上风洞实验测量值与无量纲污染物浓度K的计算值分布。无量纲浓度K定义为[23]

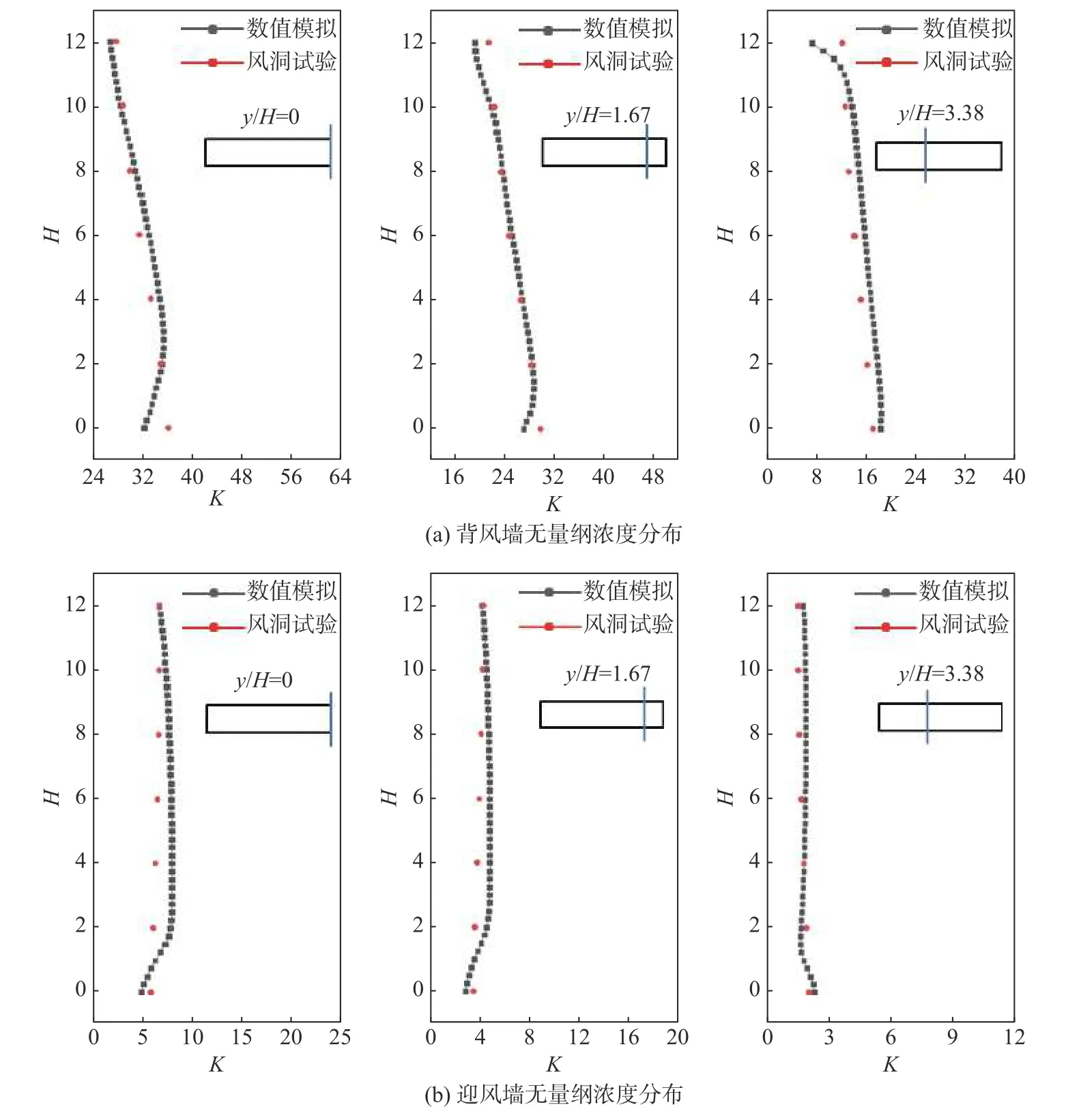
图3 不同位置处数值模拟计算值与风洞实验测量值Fig.3 Numerical simulation values and wind tunnel measurements at different positions

式中：C为污染物的体积分数；l为线源长度（l=2.24 m）；Qe为气态污染物（此处采用SF6）释放源强。

分析图3 可以观察到各位置上的计算值与实验测量值非常吻合。为了量化数值模型的性能，选择归一化均方误差（NMSE）、分数偏差（FB）、在观测值两倍因子内的预测分数（FAC2）和皮尔逊相关系数（R）对数值模型计算值和风洞实验数据之间的关联程度进行了统计学评估[30]。由表2 可知，各验证指标都在规定标准范围内。综上，本文采用标准k-ε模型研究街道峡谷内的气流运动和污染物扩散是可靠的。

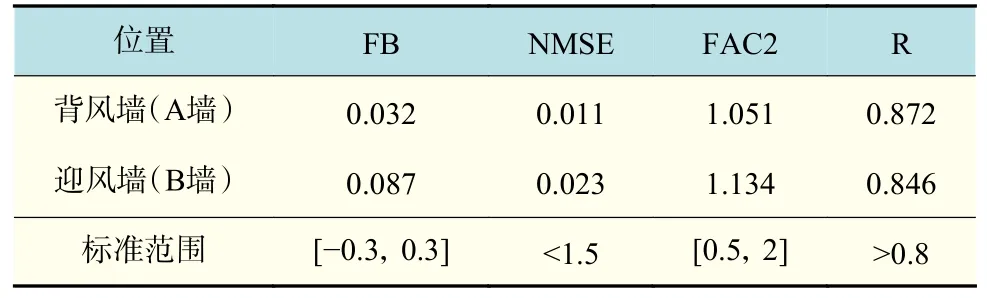
表2 数值模型评估指标Tab.2 Evaluation indicators of numerical model

2 结果与讨论

2.1 街道峡谷内流场变化与分析

图4，5，6 分别为小、中和大型树冠的街道峡谷中心垂直面的流场分布。对于小型树冠街谷（图4），当HA/HB=1 时，街谷内产生1 个顺时针涡，涡心处气流流速较低，而壁面与地面附近的流速较快；当上游建筑高度增加时，顺时针涡尺寸变大，涡心上移，并且街谷内部生成1 个新的逆时针涡，逆时针涡附近（下游建筑高度以下区域）的气流流速明显低于上部区域；对比图4（c）与4（d）可知，当上游建筑高度不变时，下游建筑的升高会导致顺时针涡涡心向上游偏移。相较小型树冠街谷，中型树冠街谷内的气流流动结构没有发生显著改变，但在HA/HB=2 的街谷内逆时针涡消失（图5（b））。随着树冠尺寸的进一步增大，HA/HB=1，街谷内的顺时针涡消失，HA/HB=3，街谷内的逆时针涡结构严重变形，涡心向迎风墙偏移，而HA/HB=2 与HA/HB=1.5 街谷内的流动结构没有发生显著变化。

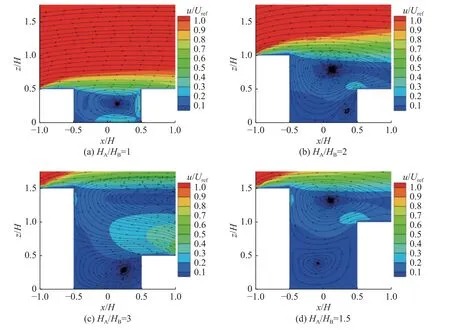
图4 小型树冠街道峡谷中心垂直面流场分布Fig.4 Flow field distribution in central vertical plane of small tree-canopy street canyon

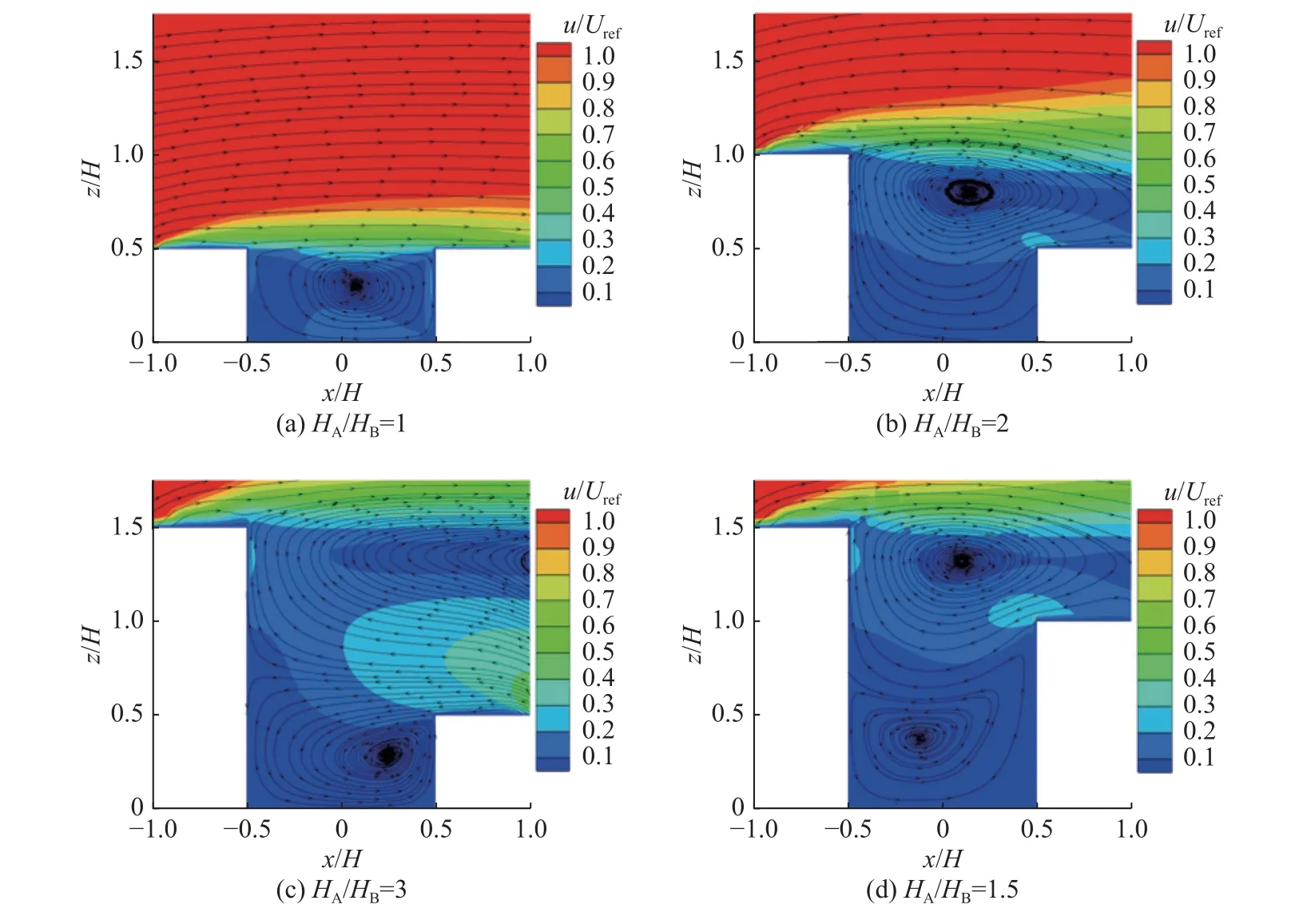
图5 中型树冠街道峡谷中心垂直面流场分布Fig.5 Flow field distribution in central vertical plane of medium tree-canopy street canyon

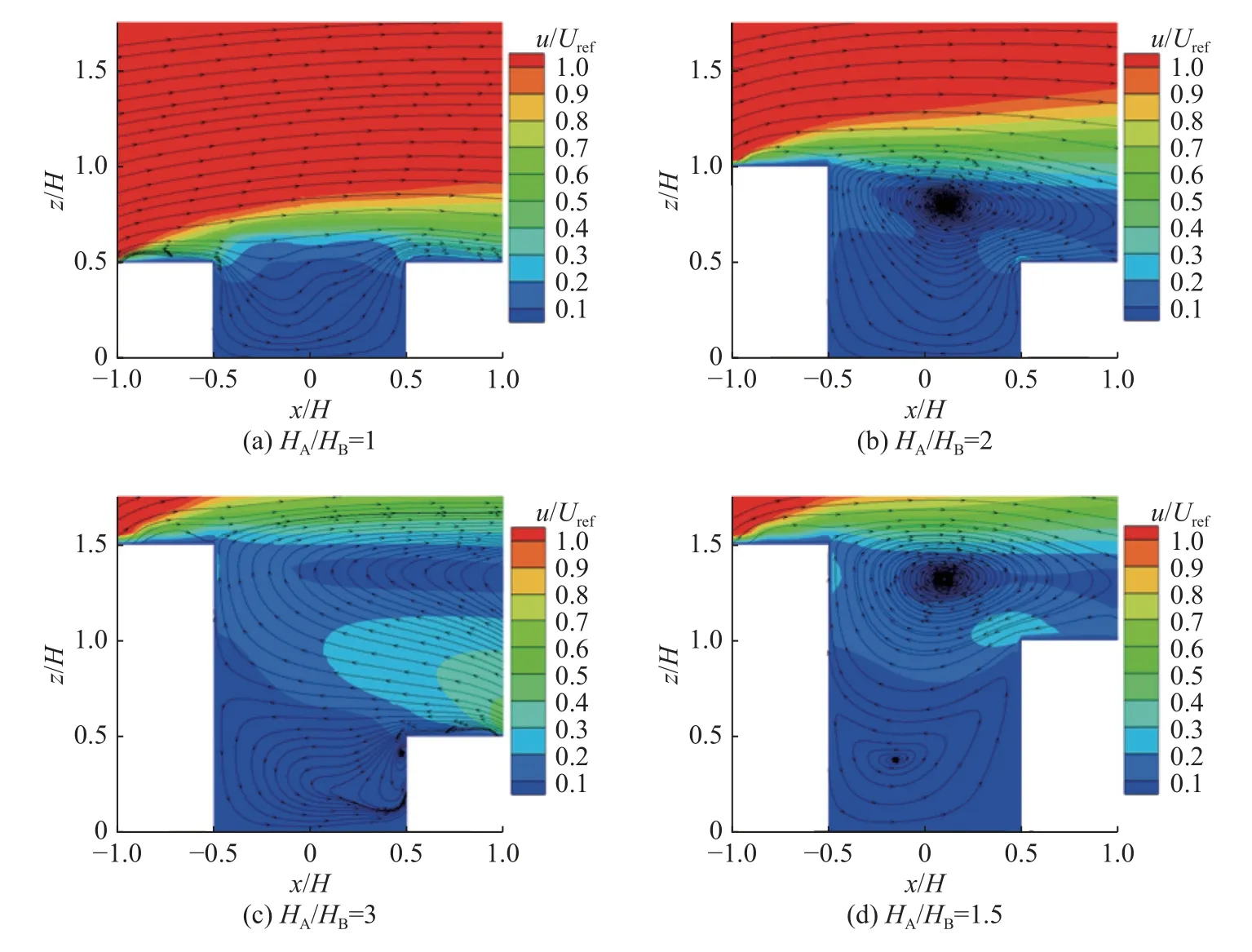
图6 大型树冠街道峡谷中心垂直面流场分布Fig.6 Flow field distribution in central vertical plane of large tree-canopy street canyon

图7，8，9 分别为小、中和大型树冠街道峡谷人行呼吸高度面的流场分布。对于小型树冠街谷（图7），当HA/HB=1 时，街谷y轴正方向出口处生成一个顺时针涡，负方向出口处则生成一个逆时针涡，街谷内气流主要向背风墙方向流动，而在大型树冠街谷内，街谷内气流则向迎风墙流动；当HA/HB=2 时，街谷内产生对向流动，气流被分成两部分，一部分往背风墙方向流动，一部分往迎风墙流动，而在中型与大型树冠街谷内，同样观察到对向流动，但流向均往背风墙方向。随着上游建筑继续增高，即HA/HB=3 时，街谷内气流对向流动发展为反向流动，分别流向两端出口；当上游建筑增高后保持不变而下游建筑增高，即HA/HB=1.5 时，街谷内气流反向流动发展为对向流动，气流主要向迎风墙流动。通过对比分析不同树冠尺寸的街谷内的流动情况可以看出，树冠尺寸的增加能够明显改变气流的流速与流动结构，这在HA/HB=1，2 的街谷尤为明显。

图7 小型树冠街道峡谷人行呼吸高度面流场分布Fig.7 Flow field distribution at pedestrian breathing height in small tree-canopy street canyon

图8 中型树冠街道峡谷人行呼吸高度面流场分布Fig.8 Flow field distribution at pedestrian breathing height in medium tree-canopy street canyon

图9 大型树冠街道峡谷人行呼吸高度面流场分布Fig.9 Flow field distribution at pedestrian breathing height in large tree-canopy street canyon

2.2 街道峡谷内污染物浓度分布

图10，11，12 分别为小、中和大型树冠街道峡谷中心垂直面的污染物浓度分布，结合图4，5，6 分析可知，街谷内污染物的分布主要受气流流动结构的影响。对于小型树冠街谷（图10），当HA/HB=1 时，污染物在街谷内顺时针涡的作用下向背风墙一侧扩散。随着上游建筑的升高，街谷内污染物受逆时针涡的影响，开始向迎风墙一侧扩散，导致迎风墙附近的污染物浓度升高，这在HA/HB=3与HA/HB=1.5 的街谷内尤为明显。由于与小型树冠街谷内的流动结构相比变化不大，中型树冠街谷内的污染物分布趋势与小型街谷内基本相似。但在大型树冠街谷内，尤其是HA/HB=1时，街谷内顺时针涡消失，气流向迎风墙流动，污染物随气流向该侧扩散，导致迎风墙一侧污染程度加剧。显然，在不同结构街谷内，树冠尺寸变化对污染物分布情况的影响程度不同，在HA/HB=2，3，1.5 的街谷内，树冠尺寸改变，街谷内污染物分布趋势变化不大，而在HA/HB=1 的街谷内，树冠尺寸增为大型时，污染物分布情况发生显著改变。

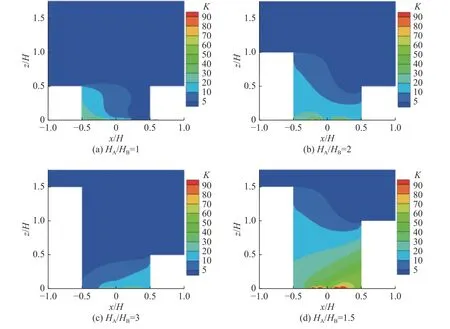
图10 小型树冠街道峡谷中心垂直面污染物分布Fig.10 Pollutant distribution in central vertical plane of small tree-canopy street canyon

图11 中型树冠街道峡谷中心垂直面污染物分布Fig.11 Pollutant distribution in central vertical plane of medium tree-canopy street canyon

图12 大型树冠街道峡谷中心垂直面污染物分布Fig.12 Pollutant distribution in central vertical plane of large tree-canopy street canyon

图13，14，15 分别为小、中和大型树冠街道峡谷人行呼吸高度面的污染物浓度分布，人行呼吸高度面污染物的分布同样受气流运动的主导。当HA/HB=1 时，对于小型与中型树冠街谷，由于气流向背风墙方向流动，污染物随之向背风墙一侧扩散；当HA/HB=2 时，人行呼吸高度面的污染物仍主要分布在背风墙一侧，但小型树冠街谷内的部分污染物有明显向迎风墙扩散的趋势。随着上游建筑继续增高，即HA/HB=3 时，街谷内污染物在气流的作用下向街谷出口端扩散，导致街谷出口附近的污染物浓度升高。而当HA/HB=1.5 时，街谷内气流对向流动，街谷中部的污染程度明显高于其他区域。对比相同结构不同树冠尺寸的街谷，随着树冠尺寸的增加，对应结构的街谷内污染物浓度明显上升，高浓度污染区域的范围明显扩大，这是由于树冠的阻滞作用抑制了污染物的扩散。

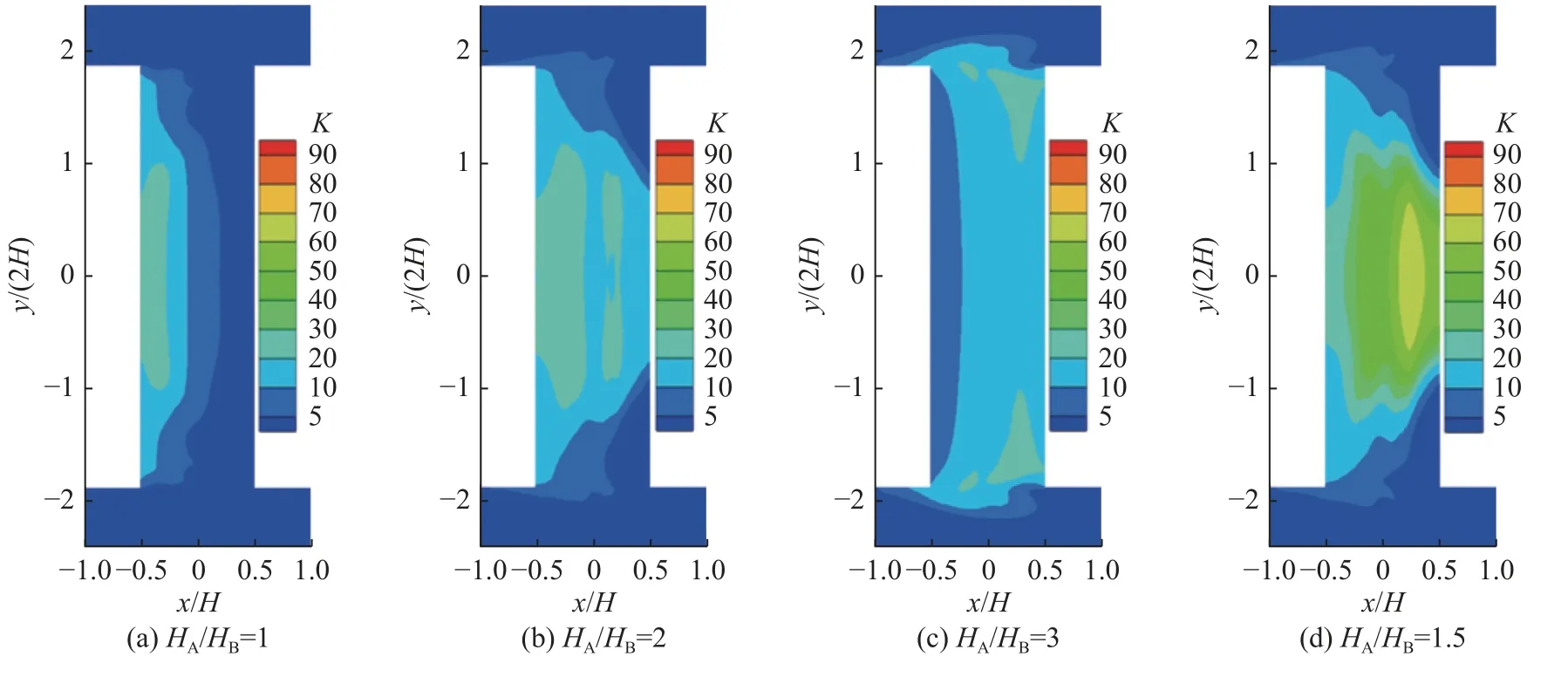
图13 小型树冠街道峡谷人行呼吸高度面污染物分布Fig.13 Pollutant distribution at pedestrian breathing height in small tree-canopy street canyon

2.3 街道峡谷内ACH 的评估分析

空气交换率ACH表示单位时间内街道峡谷和环境大气之间的空气交换量。空气从街谷排出表示为ACH+，进入街谷则表示为ACH-。对于本研究中的3D 街道峡谷，气流主要在街谷两端出口与顶部与环境空气发生交换，ACH+与ACH-的计算定义为[23,31-33]

图14 中型树冠街道峡谷人行呼吸高度面污染物分布Fig.14 Pollutant distribution at pedestrian breathing height in medium tree-canopy street canyon

式中：ACHt表示穿过街谷顶面；ACHs1表示穿过街谷y轴正向出口平面；ACHs2表示穿过街谷y轴负向出口平面。

式中：Γ表示对应平面的面积，k为湍动能。

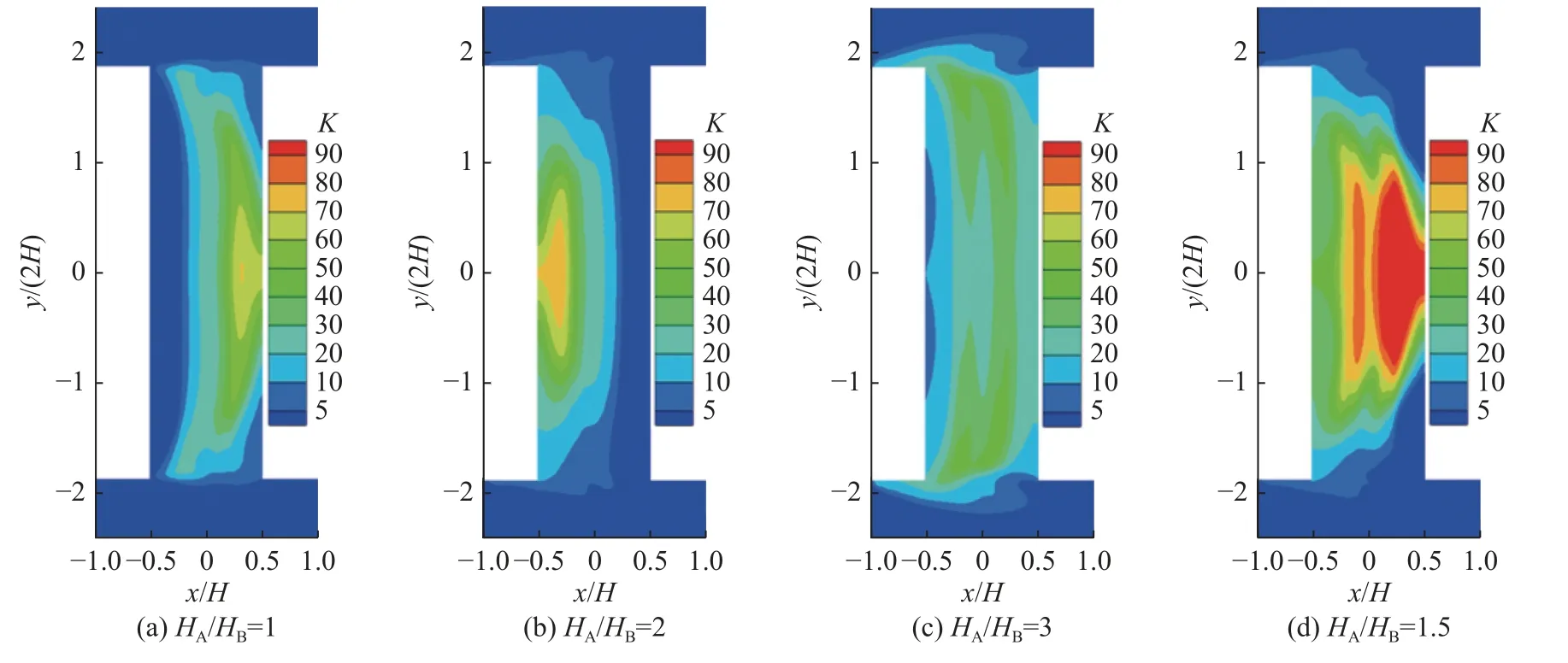
图15 大型树冠街道峡谷人行呼吸高度面污染物分布Fig.15 Pollutant distribution at pedestrian breathing height in large tree-canopy street canyon

图16 为各工况下街道峡谷内的空气交换率ACH的柱状图。由图16 可知，对于相同结构的街道峡谷，随着树冠尺寸的增加，街谷内的ACH随之降低。其中，当树冠尺寸从小型增大为中型时，在HA/HB=1，2，3，1.5 的街谷内，ACH分别降低了3.40%，10.53%，3.27%，0.99%，而当树冠尺寸从小型增大为大型时，ACH则分别降低了10.61%，28.37%，26.45，3.34%。进一步分析可知，在各结构街谷内，树冠尺寸从小型改变为中型与大型时，ACH分别平均降低了7.00%，19.45%，14.86%，2.16%。显然，在不同结构的街谷内，树冠尺寸对ACH的影响程度不同，尤其在HA/HB=1.5 的街谷内，树冠尺寸改变引起的ACH变幅很小。同时，街谷结构的变化同样会显著影响街谷内的ACH。当树冠尺寸不变，上游建筑升高时，街谷内的ACH明显降低，其中，HA/HB=3 街谷内的ACH相较HA/HB=1 街谷平均降低了42.4%，而在此情况下将下游建筑升高，即HA/HB=1.5 时，街谷内的环境通风能力得到明显提升，此时街谷内的ACH相较HA/HB=3 街谷最大升高了139.1%，平均升高了99.1%。

图16 街道峡谷内的空气交换率Fig.16 ACH in street canyons

3 结论

采用经风洞实验数据验证的标准k-ε模型，通过数值模拟研究了垂直迎风条件下，树冠尺寸与建筑高度变化对街道峡谷内环境通风和交通污染物扩散的影响，得到以下结论：

a.建筑高度的变化对街道峡谷内的气流流动结构有重要影响，因此，在不同建筑高度的街道峡谷内，污染物的扩散分布情况显著不同。上游建筑的升高会导致街谷中心垂直面逆向涡的生成以及人行呼吸高度面气流流向的改变，此时街谷中心垂直面与人行呼吸高度面上的污染物有明显向迎风墙一侧扩散的趋势。下游建筑抬高则会引起街谷上方顺时针涡尺寸的变化与涡心的偏移，此时污染物在街谷内的分布范围变广，且在迎风墙一侧浓度较高。

b.在不同结构的街道峡谷内，树冠尺寸的改变对街谷内气流流动结构与污染物扩散的影响不同。相较HA/HB=2，3，1.5 的街谷，在HA/HB=1 街谷内，树冠尺寸变化对气流结构的影响更为显著。在HA/HB=1 街谷内，对比中、小尺寸树冠情况，大型树冠会导致较矮建筑的街谷中心垂直面的顺时针涡消失以及人行呼吸高度面气流流向改变。

c.街谷内的环境通风情况会因树冠尺寸与建筑高度的改变而发生变化。树冠尺寸增大与上游建筑升高均会导致街谷内ACH降低，而下游建筑抬高则会提升街谷内ACH。为了改善现实街道的通风条件，对于HA/HB=1，2，3 的街谷，应尽量减小树冠的尺寸，而对于HA/HB=1.5 的街谷，由于树冠尺寸改变对街谷内通风影响甚小，在考虑经济性的前提下可不对这类街谷内的树冠进行过多的修剪。

研究了不同树冠尺寸与建筑高度对街谷通风与污染物扩散的影响，提出了不同结构的街道峡谷内行道树树冠的最佳修剪方式。对绿化结构进行了初步的探讨，但对实际绿化进行了一定的简化，后续研究将进一步考虑树冠对污染物的去除效果及行道树叶片类型对街谷内流动结构及污染物扩散分布的影响。