基于暂态高频分量的故障投票选线方法

吴 君，谢逸飞，张长森

(1.河南理工大学 物理与电子信息学院，河南 焦作 454000；2.河南理工大学 电气工程与自动化学院，河南 焦作 454000)

小电流接地系统以其良好的供电可靠性在中压配电网中得到广泛应用。但小电流接地系统发生单相接地故障后，故障特征微弱且不易提取，尤其是经消弧线圈接地系统的故障选线路难度较大[1]。快速判断出故障线路能够防止故障进一步扩大，保证电力系统稳定运行，因此对选线方法要求较高。根据所利用的故障信号特征可将现有的选线方法分为稳态判据法、暂态判据法和信息融合法3大类。稳态判据法在一定程度上受到零序互感器不平衡、系统运行方式以及接地电阻等的影响，对整定值的选择要求较高，选线结果容易出现偏差[2-4]。暂态判据法由于不受消弧线圈及故障因素的影响，故障特征明显，方法灵敏性较高，已成为研究热点，但易出现模态混叠及自适应能力差的问题[5-7]。信息融合法主要利用模糊网络、神经网络、模糊识别等技术来实现选线[8-9]，能够有效提高单一选线方法的准确性，但还需要进一步深入研究各种方法的权值。

针对以上不足，本文提出了一种基于暂态零序电流高频分量的波形相似性投票选线方法。该方法首先采用变分模态分解(Variational Mode Decomposition，VMD)算法对各条线路的零序电流进行分解，得出暂态高频分量；然后结合巴氏距离(Bhattacharyya)算法分别计算出两两线路间暂态高频分量的巴氏系数；最后采用初步投票与k值检验对巴氏系数进行投票从而判断出故障线路。

1 故障电流暂态特征分析

中性点经消弧线圈接地系统发生单相接地故障的暂态等效电路如图1所示。

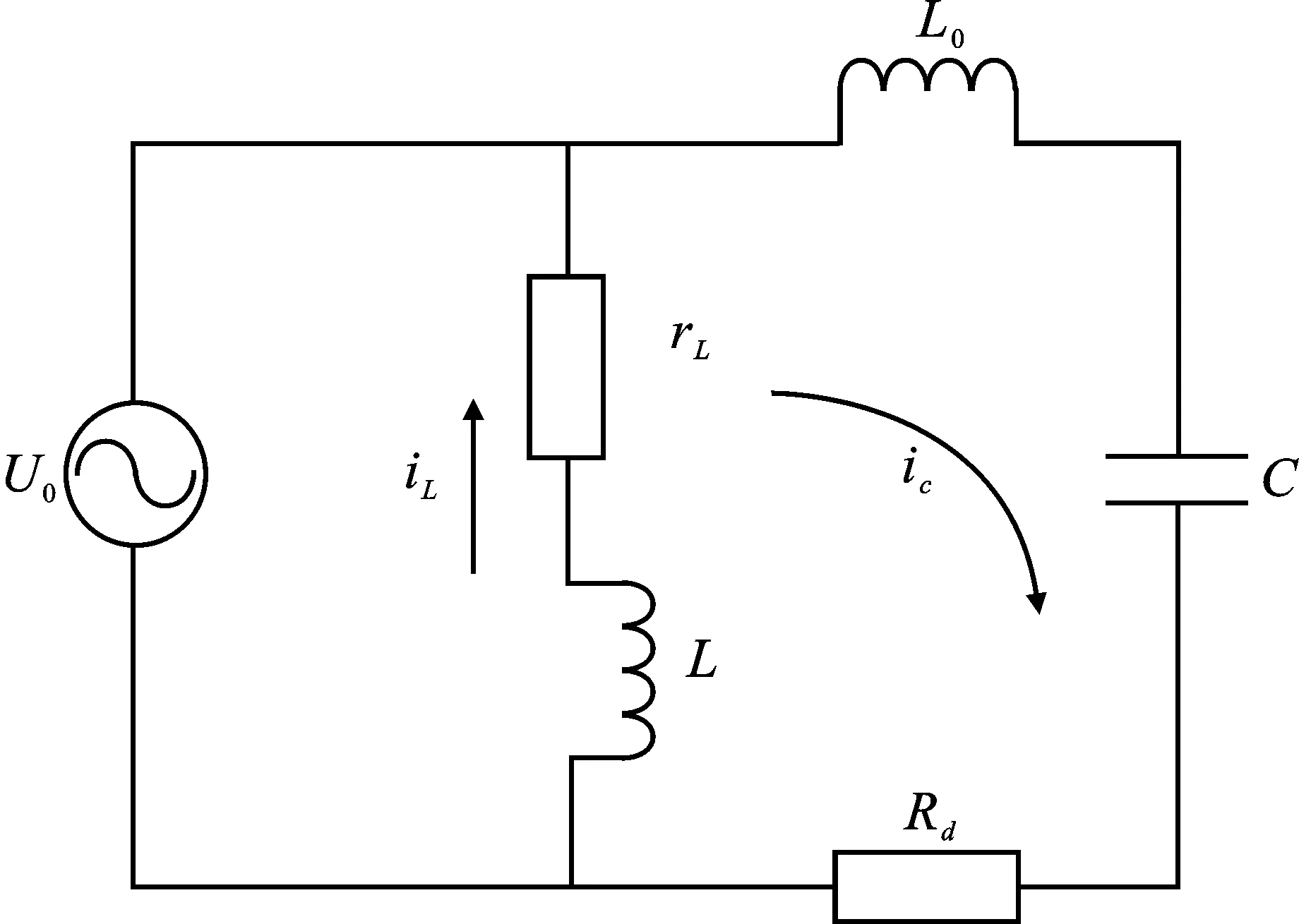
图1 单相接地故障暂态过程等值电路

图1中，U0为零序电压源，Rd为等效接地电阻，L0为等效电感，C为对地电容，rL和L分别为消弧线圈的电阻和电感。分析电路可知，暂态电容电流和电感电流叠加组成了暂态零序电流，表达式为

(1)

式中，ICm为电容电流；ILm为电感电流；ωf为暂态自由振荡分量角频率；τC和τL为时间常数。

由式(1)可知，暂态零序电流if由工频分量、衰减的直流分量及高频分量组成，由于稳态工频分量不满足选线要求，衰减直流分量只流经故障线路，故不作选线判据考虑。单相接地故障发生后，暂态过程是故障发生后与稳态之间很短的瞬时过程，大概是0.5～1个工频周波。由式(1)等号右边第3部分可知，在故障发生的初始阶段，暂态零序电流的幅频主要由暂态电容电流决定，且电容电流对暂态零序电流的特征影响更大[10-12]。由于ICm流经故障和非故障线路，且其中的高频分量包含了大部分的故障信息，可作选线判据。对ICm的分析可得出暂态高频分量特征如下：故障线路与非故障线路相位相差180°；故障线路的幅值远大于非故障线路，数值上等于所有非故障线路分量之和；母线故障时，所有出线相位一致。利用上述故障电流暂态特征进行相似度分析即可准确判断出故障线路。

2 选线判据

2.1 VMD算法

VMD算法是一种全新的混合信号分解算法，其核心思想是构造并求解变分模型。VMD算法的原理为：首先将原信号重构为带有约束条件的变分模型；然后根据预设的分解层数K和每个模态的估计带宽之和最小的原则，迭代计算出模型的最优解，从而自适应地将原信号分解为K个不同频段的IMF分量[13-15]。算法的具体步骤如下：

步骤1假设原信号为f(t)，分解层数为K，分解出的IMF分量记作uk(t)。构造变分模型需要满足如下条件：(1)u1(t)+u2(t)+ … +uk(t)=f(t)；(2)K个IMF分量的带宽之和最小；(3)每个uk(t)都有中心频率和有限带宽。

根据以上条件构造出变分模型如下

(2)

其中

uk(t)=Ak(t)cos[φk(t)]

(3)

(4)

式中，ωk为各个IMF的中心频率；δ(t)为单位脉冲函数；*为卷积运算；

步骤2引入二次惩罚因子α和拉格朗日算子λ(t)，将带有约束条件的变分模型解约束。解约束后的变分模型为[13-14]

(5)

L({uk}，{ωk}，λ)=

(6)

(7)

(8)

(9)

式中，τ为噪声容限参数；

步骤6终止条件为

(10)

迭代计算至满足条件则停止计算，得到K个IMF分量；否则继续迭代计算。

2.2 巴氏距离算法

巴氏距离算法通常用于测量两个离散数据的概率分布，其计算式为

(11)

式中，p(x)和q(x)为离散数据的概率分布函数。由于巴氏系数(BC)常用作衡量直方图相似度[15-17]，因此进行电流波形相似度计算时，需要先将故障零序电流转化为概率分布函数，再代入式(11)计算巴氏系数。巴氏系数越接近1则表明两波形越相似；巴氏系数越接近0则表明两波形差异较大。根据巴氏系数大小只能判断出故障线路的范围，因此进一步提出选线机制才能准确判断出故障线路。

3 故障投票选线机制及流程

对于任一线路Li，定义G值为

(12)

式中，i、j、j′为线路编号；Mij为线路li与线路lj的巴氏系数；Mij′为除min(Mij)外的巴氏系数。对于一个具有n条出线的系统，提出故障选线投票机制如下：

步骤1实时监测系统零序电压，根据整定值判断是否发生单相接地故障及启动选线程序；

步骤2提取故障后各线路首个T/4周期零序电流，用VMD算法进行分解，得到暂态高频分量；

步骤3将各线路的暂态高频分量转化为概率分布函数，并用巴氏距离算法求出两两线路间的巴氏系数；

步骤4假设l1为健全线路，则min(M1j)对应的lj为故障线路作为初步投票结果；

步骤5初步投票结果不一致时，对其进行G值检验，若min(G)<ε，则l1为故障线路；若min(G)>ε，则Lj为故障线路(ε为设定的阈值)[18-19]；

步骤6对各条线路执行步骤4、步骤5可以得到n个投票结果，对以上n个投票结果采用少数服从多数原则判定出故障线路。

基于以上理论，小电流接地系统单相接地故障投票选线流程如图2所示。

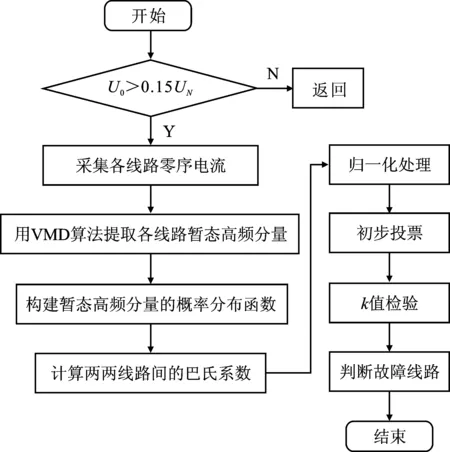
图2 故障选线流程图

4 仿真分析

4.1 仿真模型

使用MATLAB搭建10 kV中压配电网的小电流接地系统，共4条出线。本文选择中性点经消弧线圈接地系统，采用过补偿方式运行，补偿度为10%。线路正序参数为R1=0.195 Ω·km-1，L1=1.23×10-4

H·km-1，

C1=8.5×10-6F·km-1。线路零序参数为R0=0.743 Ω·km-1，L0=5.47×10-4H·km-1，C0=6.7×10-7F·km-1，L=0.352 8 H，rL=3.323 Ω。线路l1=25 km，l2=30 km，l3=35 km，l4=40 km，如图3所示。限于篇幅，以下只给出几种典型单相接地故障的仿真分析结果。

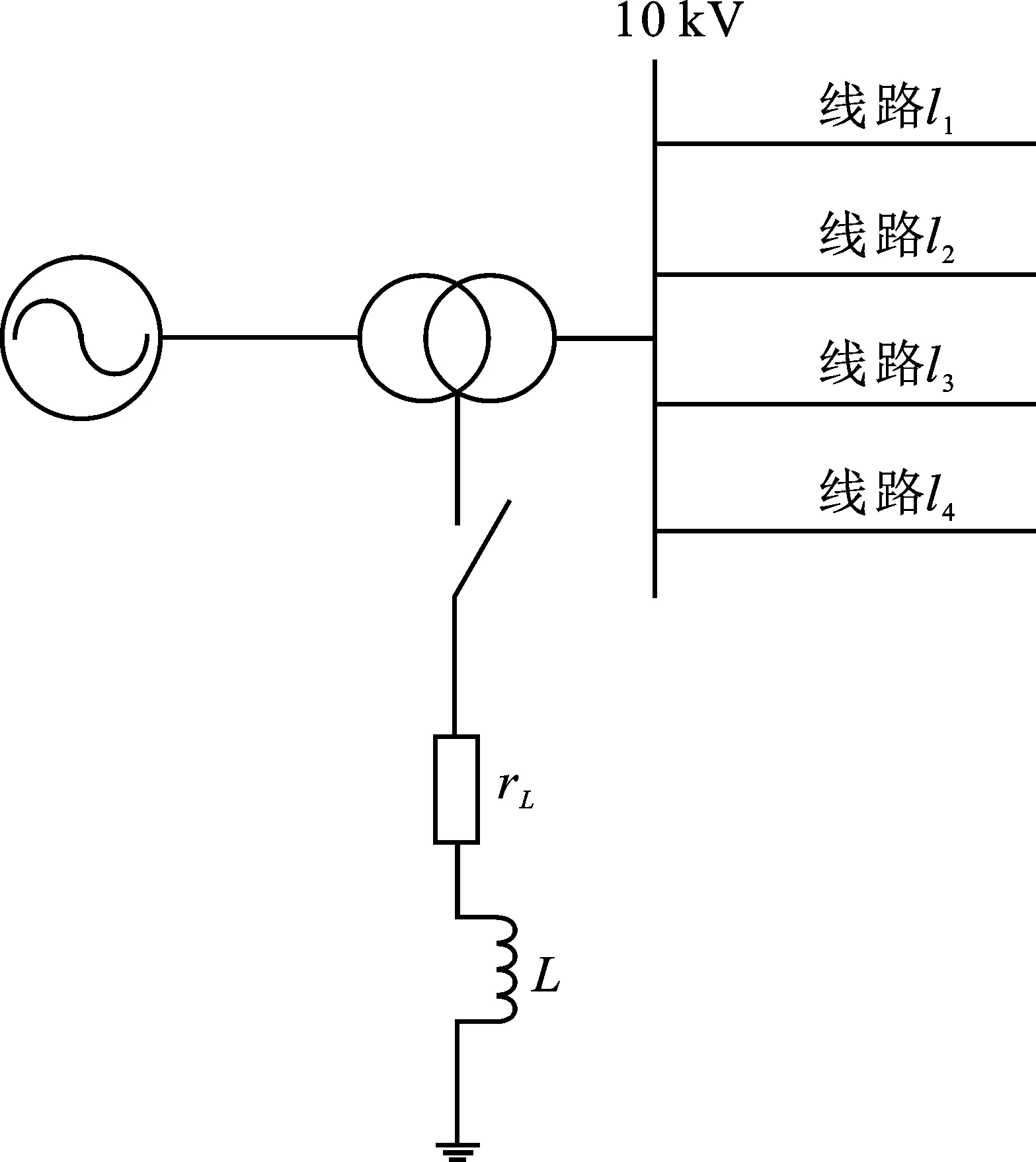
图3 小电流接地系统仿真模型

4.2 算例分析

以线路l4在0.02 s时发生单相接地故障为例，故障初相角设为30°，故障电阻为10 Ω，故障线路零序电流如图4所示。以10 kHz的采样频率提取出各线路故障后的零序电流，根据VMD算法的自适应性及暂态分量频率在300～3 000 Hz的特点，将分解层数K设为3，α设为20 000，τ设为0，分解后的各分量如图5所示。

图4 线路零序电流

图5 故障线路暂态高频分量

图5中，IMF-1、IMF-2和IMF-3分别为衰减的直流分量、交流分量以及高频分量。该结果说明VMD算法能够有效直观地对零序电流进行分解，进而提取出高频分量。各条线路的高频分量如图6所示。

图6 各线路暂态高频分量

分别获得两两线路的高频分量在同一时间窗下的概率分布函数：取最大值和最小值之间的幅值为波动区间，并等分为10个子区间。分别统计两条波形落在子区间的数据个数，即可建立概率分布函数。部分线路的高频分量波形分布直方图如图7所示，进一步计算出巴氏系数，结果如表1所示。

(a)

表1 各线路之间巴氏系数

由表1中数据可以看出，M41、M42、M43数值较小，且都在0.15以下。M12、M13、M21、M23、M31、M32数值较大，根据巴氏距离理论，表明故障发生后线路l4与l1、l2、l3零序电流差异较大，线路l1、l2与l3之间差异较小，波形较为相似。利用投票机制可得初步投票结果如表2所示。

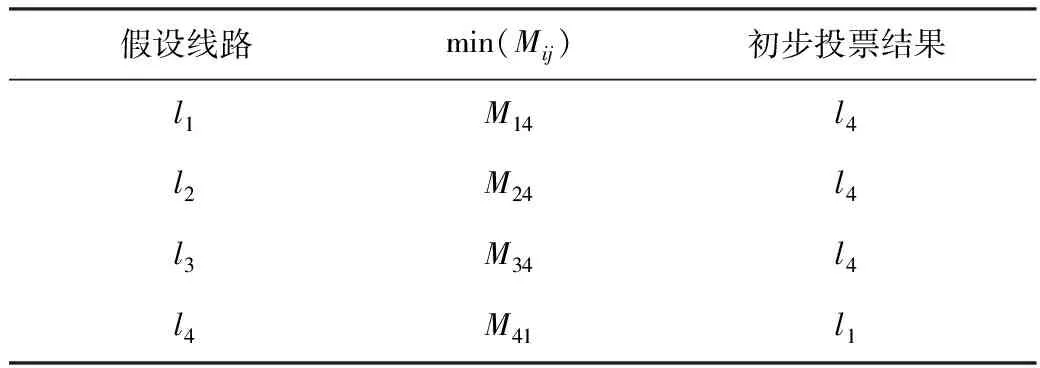
表2 初步投票结果

由表2可以看出，初步投票结果并不一致，此时必须进行k值检验，从而准确选出故障线路。由式(12)计算出的k值为

(13)

出于系统波动等非故障因素影响的考虑，经过大量仿真，本文中ε值取3较为准确。k值检验后的最终投票结果如表3所示。

表3 最终投票结果

表3数据中，l1、l2与l3的min(G)均大于ε，证明初步投票结果正确。线路l4的min(G)小于ε，修改投票结果，最终确定故障线路为l4，与实际一致。不同故障条件下的选线结果如表4所示，数据表明该方法在不同故障情况下具有较好的适应性。

表4 不同故障条件下的选线结果

4.3 选线结果对比

使用现有的暂态选线方法，分别在不同故障条件下进行仿真实验，得出100组试验后的正确率，结果如表5所示。

表5 选线正确率对比

由表5中数据可以看出，相比小波分解法和经验模态分解(Empirical Mode Decomposition，EMD)算法，本文提出的方法选线正确率有较大提高，但仍存在一定死区，经多次仿真实验得出死区主要出现在故障初相角处于17°～20°时。经分析可知，出现死区的原因为VMD算法分解层数在故障初相角较小时容易出现虚假分量，造成选线错误，因此仍需进一步优化分解层数K。

5 结束语

本文首先分析了小电流接地系统单相接地故障的暂态零序电流特性，确定了将线路间暂态高频分量的差异性作为选线判据，利用VMD算法对各线路的零序电流分解得出暂态高频分量，再利用巴氏距离算法分别计算出两两线路间暂态高频分量的巴氏系数，从而初步判断出故障线路的范围。在此基础上，进一步利用投票机制即可准确判断故障线路。对比小波分析法和EMD法，本文所提方法在不同频率下的自适应性较好，且能够避免模态混叠的问题。仿真表明，相较于只利用相似系数大小来判断故障线路，本文所提机制充分利用了波形相似性，具有较好的选线精度。

本文的不足之处在于VMD算法分解层数的确定仅通过理论分析得到，需要进一步优化以减少死区并提高选线准确性，且投票机制仍需进一步优化以适应母线接地故障。