改进的蒙哥马利模乘算法及FPGA实现
2022-07-13程碧倩刘光柱
程碧倩,刘光柱,肖 昊
(合肥工业大学 微电子学院,安徽 合肥 230009)
随着互联网和云计算技术的飞速发展,网络购物、网络支付、云存储等互联网新经济迅速发展,方便了人们的生产生活。但由于互联网存在开放性,因此保障云数据和云交易的安全成为工业界和学术界关注的焦点。目前,利用公钥密码系统(Public Key Cryptosystem,PKC)对数据信息进行加密或签名保护是保障网络信息安全的主要方法之一[1-3]。大整数模乘运算是PKC的核心运算,其计算效率对PKC的性能至关重要。蒙哥马利模乘算法作为一种高效率的模乘算法,能够避免模乘中的除法运算,减少模乘的计算量,是优化大整数模乘计算效率的研究重点[4-5]。
目前,国内外关于蒙哥马利模乘算法的优化已有不少研究成果。按照其研究目的,主要分为两类:一是提高计算时间;二是减少逻辑资源。文献[6~8]采用Karastuba算法或基于该算法的衍生算法对输入数据进行变形,降低计算的复杂度,并进行全展开的256 bit模乘运算,大幅提高了计算速度,缩短了计算时间。但对于大位宽模乘(如1 024 bit、2048 bit等),该方法需消耗大量逻辑资源。文献[9]采用蒙哥马利模乘算法,减少了计算的逻辑资源,但其每次运算仅能处理2 bit乘法,因此需经过多次迭代完成模乘运算。尽管该算法节省了大量的逻辑资源,但其速度仍有待提升[9]。
针对大位宽模乘运算,为了更好地平衡其计算时间和逻辑开销,本文提出了一种多项式展开的交叉蒙哥马利模乘算法,并基于现场可编程门阵列(Field Programmable Gate Array,FPGA)设计实现了1 024 bit多项式展开的交叉蒙哥马利模乘算法。本文对所提算法的正确性进行了验证,并对其性能进行了对比分析。
1 算法介绍
假设有3个长度均为nbit的二进制大整数A、B和M,其中A与B范围在0~M。模乘运算表示为S=A×BmodM,通常情况下,先计算A、B的乘积然后再计算modM。经典蒙哥马利模乘算法用简单的移位运算代替耗时的取模运算。本文在此基础上提出了一种灵活度高、低成本、高效的多项式展开的交叉蒙哥马利模乘算法。
1.1 经典蒙哥马利模乘算法
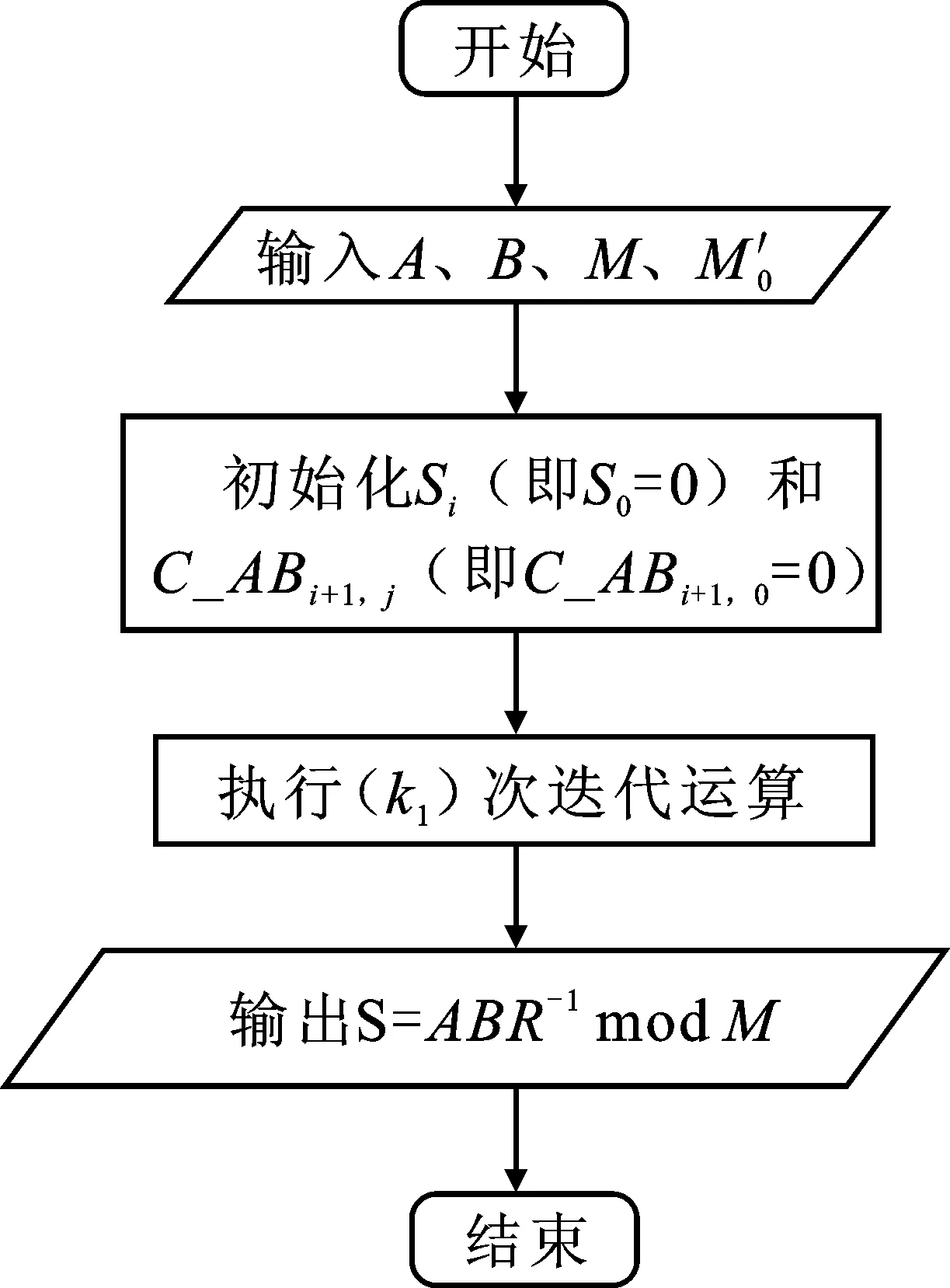
经典蒙哥马利模乘算法的设计思想是利用剩余系性质,借助构造一个模M的剩余系,将普通求模运算转化成移位和加法运算[10-13]。蒙哥马利算法完成S=A×B×R-1modM。选择满足0≤A,B R×R-1=1 modM (1) M′=-M-1modR (2) 经典蒙哥马利算法的实现,主要经过以下4个步骤: 步骤1将大整数A和B相乘,得到乘积T,称此步骤为模乘法操作; T=A×B (3) 步骤2取乘积T的低n位,并与模数的逆M′相乘,取乘积的低n位,得到商数q q=((TmodR)×M′)modR (4) 步骤3将商数q乘以模数M,加上乘积T,取结果的高n位,称此步骤为模约简操作 S=(T+qM)/R (5) 步骤4判断(S>M)是否成立,若成立返回(S-M),否则返回S。 通过对经典蒙哥马利算法分析并结合式(2)得到 q×M=T×M′×M≡-TmodR (6) 且S×R≡TmodR,即S≡T×R-1modM。由于0≤T+q×M 可以看到,在经典蒙哥马利算法中,逻辑操作包括两次nbit的大整数乘法和两次2nbit的大整数加法,位宽越大,逻辑操作越复杂,耗时越长。因此,本文主要通过两方面实现对算法的改进:(1)对输入数据进行多项式展开确定每次参与运算的数据位宽;(2)针对模乘法操作和模约简操作的开展方式进行调整。 本文对经典蒙哥马利模乘算法做了改进,得到多项式展开的交叉蒙哥马利模乘算法,其由两个外循环组成,称为循环1和循环2。其中,循环1求取模约简运算中的中间参数qi;循环2经多次迭代完成模乘法运算和模约简运算,并在其内嵌的小循环(循环3)中完成单次迭代的模乘法运算及模约简运算。 在该算法中,输入参数:模数M、乘数A、被乘数B,其多项式表达分别为 k2=n/y (7) 0≤A≤2M,k2=n/y (8) 0≤B≤2M,4M<2k1x (9) 输入参数:M′0,它为模数M的逆(即M′)的低xbit,S0= 0。 输出参数:S。 该算法步骤如下: 步骤1依次取B的xbit(即bi)乘以A的低xbit(即A[0]),并加上中间结果Si的低xbit(即Si[0]),完成乘累加运算后保留低xbit并乘以M′0,然后取低xbit得到参数qi: For(i=0 tok1-1)//循环1 If(i=0)ThenSi=0//初始化 步骤(1)qi=(((Si[0]+A[0]×bi)modx)×M′0) modx End for 步骤2本算法采用由循环2和循环3组成的二重循环。在每次内循环(循环3)中,每次取A的ybit(即aj)依次乘以B的xbit(即bi,其中i取0~30),并累加上一次循环结果Si的ybit(即Si,j)和进位C_ABi+1,j完成乘累加运算,得到模乘法结果。随后,将qi乘以模数M的ybit(即mj),并和上一级进位C_qmi+1,j以及S_ABi1,j+1做连续累加,完成模约简运算: For(i=0 tok1-1)//循环2 If(i=0)ThenSi=0//初始化 步骤(2)For(j=0 tok2-1)//循环3 If(j=0)ThenC_ABi+1,j=0;//初始化 步骤(2a)(C_ABi+1,j+1,S_ABi+1,j+1)=bi× aj+Si,j+C_ABi+1,j 步骤(2b)(C_qmi+1,j+1,S_qmi+1,j+1)=qi× mj+S_ABi+1,j+1+C_qmi+1,j End for Si+1=S_qmi+1/x End for 步骤3本算法通过扩大输入数据范围,省去经典蒙哥马利模乘算法的减法操作[14-15]。计算结束,输出结果S。 本算法的改进主要集中在两方面:(1)多项式展开执行逻辑运算的数据位宽;(2)模乘中涉及的乘法和模约简操作开展方式。 1.2.1 多项式展开 假设nbit的大整数B以rB为基表示,B=(bk1-1,bk1-2,…,b1,b0)rB,取rB=2x,每部分用bi表示,bi范围在0~x,通过式(7)计算得到。其中,i取0~k1-1,整数x和整数k1满足4M< 2^(k1x),得到k1bit的大整数B(式(8))。 bi=(B>>(x×i))modrB (10) (11) 另外,k1bit的大整数B也可按照(k1-1)次的多项式展开,如式(9)所示,其中,dB=rB。 (12) 同理,假设nbit的大整数A以rA为基表示,A=(ak2-1,ak2-2,…,a1,a0)rA,取rA=2y,每部分用aj表示,aj范围在0~y,通过式(10)计算得到。其中j取0~k2-1,k2=[n/y],则得到A为 aj=(A≫(dA×j))modrA (13) (14) 此外,k2bit的大整数A也可按照(k2-1)次的多项式展开,如式(12),其中dA=rA。 (15) T=A×B=A(dA)×B(dB)= (16) 若输入的数据为nbit的乘数A和被乘数B,计算过程中最多会产生2nbit的中间结果;若对输入数据以多项式形式展开,执行多精度计算,每次仅取部分A、B(即aj与bi)执行乘法运算,产生的中间结果缩小至(x+y)bit。在硬件实现中,该乘法器可被复用,其大小将影响电路的使用面积,执行本操作有利于节省面积开销。 1.2.2 模乘法和模约简交叉执行 本文利用上述多项式展开模乘算法中涉及的乘法和模约简运算,并结合多项式展开的交叉蒙哥马利模乘算法里的步骤2进行举例说明。步骤2主要由循环2和循环3组成,循环2内嵌循环3,循环3完成式(14)和式(15)的运算,分别实现模乘法(步骤(2a))和模约简操作(步骤(2b))。循环2的计算如式(16)所示。 =bi×A (17) =qi×M+S_ABi+1 (18) =q×M+B×A (19) 经典的蒙哥马利模乘算法先进行模乘法操作,再完成模约简运算。本文提出数据以多项式展开来交叉执行模乘法和模约简运算,相比经典的蒙哥马利模乘算法,本文所提算法每次仅执行小位宽的模乘法运算,便可开始执行模约简运算,缩短了模约简开始计算的时间。若采用两组乘法单元分别完成模乘法和模约简功能,可实现多组数据并行执行,进一步提高了大整数模乘计算效率。 综上,基于上述两方面改进得到的模乘算法更适合大整数模乘运算的硬件实现。其每次仅以小位宽交替执行模乘法操作和模约简操作,提高了计算效率。新算法通过减少乘法器的面积节省了硬件资源,实现低资源消耗的高效模乘。 为了验证所提算法的正确性及性能,本文对其进行FPGA实现。本节内容主要由两部分组成:(1)介绍基于多项式展开的交叉蒙哥马利模乘算法的计算流程及其硬件结构;(2)先对本文提出算法的正确性进行硬件仿真,再将本算法和经典蒙哥马利模乘算法性能进行对比,最后与其它文献基于FPGA实现的模乘算法进行性能对比。 图1为多项式展开的交叉蒙哥马利模乘算法计算流程图。当输入数据给定后,初始化Si(即S0=0)和C_ABi+1,j(即C_ABi+1,0=0),然后进入k1次迭代运算,迭代完成后输出结果,即结束运算。 图1 多项式展开的交叉蒙哥马利模乘计算流程图 图2为改进算法的硬件结构图,由多个乘累加单元、乘法器构成。计算过程主要分为3个阶段进行:(1)第1阶段。将B的xbit(即bi)与A的低xbit(即A[0])以及部分结果Si的低xbit(即Si[0])作为输入,经过k1次迭代,在乘累加单元1里完成乘累加运算,并保留运算结果的低xbit,和乘累加单元1的另一输入M′0相乘,保留低xbit得到参数qi;(2)第2阶段。以ybit为单位从A的低位到高位得到aj,乘以bi并叠加上轮迭代结果Si,j(其中Si,j为Si的ybit,j取0~k2-1)和上一级进位C_ABi+1,j,经过k1次迭代,在乘累加单元2内完成对应的模乘法运算;(3)第3阶段。将第1阶段得到的商参数qi依次与模数M的ybit(即mj)相乘,并加上模乘法结果S_ABi+1,j+1和上一级进位C_qmi+1,j,在乘累加单元3内完成模约简操作。经过这3个阶段的计算,实现1 024 bit的多项式展开的交叉蒙哥马利模乘算法。 图2 多项式展开的交叉蒙哥马利模乘的硬件结构 本文使用Verilog HDL对所提多项式展开的交叉蒙哥马利模乘算法进行RTL级实现,并使用Vivado2017.4进行功能仿真和逻辑综合。图3为其中一组随机产生的测试数据(十六进制)及其对应的计算结果。该结果与图4的仿真结果一致,证明了本文算法的正确性。其中A和B为输入数据,M为模数,M′0为模数M的逆的低xbit。图4的start信号拉高,启动模乘计算,done信号拉高,计算结果为S。 图3 测试数据及结果 图4 测试仿真图 为了更好地量化多项式展开的交叉蒙哥马利模乘算法的性能,将本文提出的算法和经典蒙哥马利算法进行性能对比,如表1所示。其中,存储空间由输入数据和运算单元的资源开销两部分组成。对于经典蒙哥马利模乘算法,设输入数据均为nbit,故A、B、M、M′消耗4n存储空间,乘法器位宽为2n(代表A×B或q×M),加法器位宽为2n+1,存储器可被复用,故运算单元的存储空间占用(2n+1)bit,因此共消耗(4n+2n+1)bit存储空间。对于本文提出的算法,输入数据拆分成xbit和ybit(其中x=[(n+2)/k1],y=[n/k2]),故A、B、M、M′0共消耗(3n+x)bit存储空间,两个乘法器位宽分别为x+y(代表aj×bi)与2x(代表A[0]×bi),两个加法器位宽分别为x+y+2(代表步骤(2a)或(2b))与2x+1(代表步骤(1)),因此存储空间共消耗(3n+x+2×(x+y+2)+2x+1)bit(其中2×(x+y+2)为乘累加单元2和3的存储开销之和,(2x+1)为乘累加单元1的结果存储空间)。由于k1和k2的取值通常大于10,因此x和y远小于n,故表1中本算法的3个性能参数均远小于经典的蒙哥马利模乘算法。综上所述,本文提出的算法相比经典蒙哥马利算法,节省了大量的硬件资源。 表1 两种算法性能对比 本文实验在Xilinx Virtex7 FPGA上实现,芯片型号是XC7VX485T,验证选取参数x=48,y=34,dA=248,dA=234,k1=22,k2=31,提出的多项式展开的交叉蒙哥马利模乘算法计算1次1 024 bit的模乘运算,经过353个周期,在237 MHz工作频率下耗时1.62 μs,消耗2 317个LUT和131个DSP。 基于FPGA实现的不同蒙哥马利模乘算法性能的比较如表2所示,其中LUT和DSP的使用数量代表了算法的逻辑开销情况,反映了相应算法的复杂度;面积时间积AT1(AT1=LUT的使用数量×时间×10-3)和AT2(AT2=DSP的使用数量×时间×10-3)用以评估算法的计算效率和逻辑开销的折衷性能[12]。文献[16]使用了27个DSP和13 811个DSP,完成1 024 bit模乘运算耗时3.60 μs。本文相比文献[16]提高55%的计算速度,节省了90% LUT数量,减少了93.2%的AT1,仅增加1倍的面积时间积AT2。文献[17]使用22 625个LUT,耗时1.01 μs完成1 024 bit模乘运算。本设计相比于文献[17]节省了89.8%的LUT资源,减少了85.2%的面积时间积AT1,仅增加131个DSP。本文相比文献[18]减少96.5%的AT1,减少69%的AT2。经上述分析可见,本文提出的算法相比其它参考文献,可更好地平衡1 024 bit蒙哥马利模乘运算的计算时间和面积开销。 表2 不同蒙哥马利模乘算法的性能比较 本文分析了经典的蒙哥马利模乘算法,提出了一种改进的蒙哥马利算法,即多项式展开的交叉蒙哥马利模乘算法。该算法通过对数据以多项式展开来交叉执行模乘法和模约简运算,可实现低成本、高效的模乘。本文基于FPGA对所提算法进行了验证,结果表明本文算法具有良好的灵活性和通用性,不仅可以在FPGA平台上实现,也可应用到其他平台。1.2 多项式展开的交叉蒙哥马利模乘算法


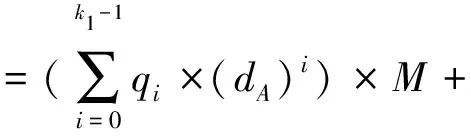
2 算法实现与性能分析
2.1 算法功能实现

2.2 性能与分析




3 结束语
