Generalized nested logit-based stochasticuser equilibrium model with distance constraint of electric vehicles

Yan Dongmei Guo Jianhua Park B.Brian

(1Intelligent Transportation System Research Center, Southeast University, Nanjing 211189, China)(2Department of Engineering Systems and Environment, University of Virginia, Charlottesville 22904, USA)

Abstract：Considering the range anxiety issue caused by the limited driving range and the scarcity of battery charging stations, the conventional multinomial logit(MNL)model with the overlapping path issue was used in route choice modeling to describe the route choice behavior of travelers effectively.Furthermore, the generalized nested logit-based stochastic user equilibrium(GNL-SUE)model with the constraints of multiple user classes and distance limits was proposed.A mathematical model was developed and solved by the method of successive averages.The mathematical model was proven to be analytically equivalent to the modified GNL-SUE model, and the uniqueness of the solution was also confirmed.The proposed mathematical model was tested and compared with the GNL-SUE model without a distance limit and the MNL-SUE model with a distance limit.Results show that the proposed mathematical model can effectively handle the range anxiety and overlapping path challenges.

Key words：traffic engineering; stochastic user equilibrium; generalized nested logit; multinomial logit; method of successive averages; distance limit

Road traffic is one of the main sources of energy consumption and environmental pollution because vehicles on the road are dependent on oil-derived fuels in conventional gasoline vehicles(GVs).These fuels accelerate energy consumption and generate large amounts of tailpipe emissions of pollutants, such as NOxand VOCs[1].Instead of gasoline-powered automobiles, automotive manufacturers and research institutes are striving to look for new types of vehicles, such as electric vehicles(EVs), to cope with these problems[2].Compared with conventional GVs, EVs, especially battery EVs(BEVs), can significantly reduce greenhouse emissions and mitigate excessive consumption of fossil fuels[3-5].BEVs are also known to rely entirely on electricity.The electricity consumption of BEVs is generally proportional to the driving distance, and the driving range of BEVs is limited by the battery capacity.BEVs cannot be driven any farther longer once their driving distance is larger than their driving distance limitation because the battery storage of BEVs has been exhausted, and public electricity-charging stations of BEVs are insufficient[6].In this case, the fear of running out of batteries while traveling has led to the so-called range anxiety issue.Battery storage and charging technologies have experienced significant progress, and the number of new public charging stations is also increasing.However, range anxiety remains to be one of the main barriers hindering the widespread acceptance and adoption of BEVs[7].A general belief is that range anxiety might not be completely eliminated in the near future[8-9].Range anxiety will continue to affect the travel choices of BEV drivers.Therefore, the range anxiety issue must be properly addressed in the process of traffic assignment modeling, particularly for regions where BEVs are expected to grow rapidly.

Studies on incorporating range anxiety issues into the traffic assignment model have been conducted in the literature.Jiang et al.[8]proposed a user equilibrium(UE)model with a distance limit, which is described by setting the path flow to zero when the path length exceeds the driving range limit.Jiang et al.[10]further extended the model to investigate the coexistence of GVs and BEVs, as well as their combined choices of destination, route, and parking, which are affected by the distance limit.Jiang et al.[6]formulated a network equilibrium problem regarding the selection of modes and routes based on travelers who own GVs and BEVs and analyzed the effects of operation costs and distance limits on vehicle and route choices of these travelers.However, these studies did not consider the behaviors of BEV users at the charging stations.To this end, He et al.[9]and Xie et al.[11]considered the time required for recharging and incorporated the relay requirement of EVs in their long-haul trips, which is typically beyond the distance limit.Xu et al.[12]developed a mathematical model for the UE problems by considering battery swapping stations and road grade constraints.On this basis, Liu et al.[13]presented the UE conditions to describe the route choice behaviors of BEV drivers considering flow-dependent electricity consumption.Tran et al.[14]developed a bi-level optimization framework to determine the optimal location of public fast-charging stations.Notably, the abovementioned traffic assignment models are mainly in the UE context.In this regard, Jing et al.[15]formulated a general MNL-based SUE model with a distance limit to extend the UE model.Riemann et al.[16]proposed a mixed-integer nonlinear model to determine the optimal location of wireless charging facilities for EVs.The model considers the interaction between the facility location and the traffic flow pattern captured by the MNL-based SUE model.Yang et al.[17]proposed a stochastic UE model for EVs by considering travel time, energy consumption, and charging service time.Huan et al.[18]proposed a dynamic traffic flow assignment model considering the en-route fast-charging behavior of users.Gao et al.[19]proposed a bilevel model to investigate the interaction between traffic flow distribution and the location of charging stations in a hybrid network of EVs and traditional GVs.

Traffic assignment is a fundamental technique for transportation management.The stochastic user equilibrium(SUE)-based traffic assignment model has been widely adopted to deal with various perceptions of travelers.Most SUE models in the literature use the multinomial logit(MNL)route choice model.However, the assignment results are generally inadequate or impossible to account for similarities between different paths, that is, the overlapping path issue, due to the well-known IIA property of the MNL model[20], Daganzo et al.[21]proposed the multinomial probit(MNP)model, which has an advantage that the similarity between alternatives can be considered.However, the MNP model is computationally unattractive because its probability function is not a closed form.In addition, other discrete choice models that can capture similarity among various routes have been extensively studied.The first category is modifications to MNL, such as C-logit[22-23]and path-size logit[24-25], which capture similarities through additional terms in the systematic utilities of the various routes.The second category is the generalized extreme value theory, such as the paired combinatorial logit(PCL)model[26-27], cross-nested logit(CNL)model[28-30], and generalized nested logit(GNL)model[31],which capture similarities by allowing additional general correlation structures.Notably, the PCL and CNL models are special cases of the GNL model.Furthermore, some researchers have adopted the GNL-based route choice model in the SUE modeling process.Bekhor et al.[31]proposed a mathematical formulation of the SUE model with GNL by adding an entropy term to the objective function.Li et al.[32]extended the model in Ref.[31]to formulate a GNL-based multiclass multicriteria SUE model.From a different perspective, Koppelman et al.[33]proposed a heterogeneous GNL model that allows for heterogeneity in error variance and covariance structure to represent the complex behavioral processes involved in choice decision-making.

The range anxiety and overlapping path issues are essential or critical for traffic assignment with motor vehicles involving BEVs.Numerous studies were proposed to address the overlapping path and the range anxiety issues in traffic assignment.However, none of these models addressed the two issues together.Thus, this paper aims to develop and evaluate a framework addressing the two issues simultaneously.Hence, a generalized nested logit-based SUE(GNL-SUE)model with multiple user classes(i.e., GV and BEV users)and distance limits was designed.In addition, the analytical solution was proposed to solve this modified GNL-SUE model.

1 Generalized Nested Logit Model Review

The GNL model is described as a two-level nesting structure.Specifically, the upper layer comprises all links(nests)in the network, and the lower layer includes all paths(alternatives)in the path set.Assuming that this structure is adopted, the probability of choosing pathkfor user classibetween O-D pairwis then given by

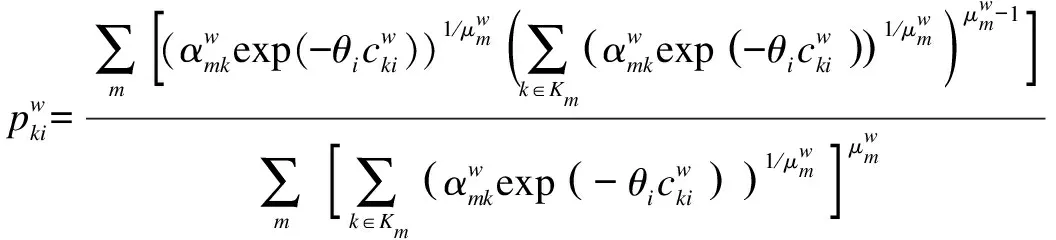
∀w,i,k

(1)

Eq.(1)can be further decomposed into marginal and conditional probabilities, and the expression may be rewritten as

(2)

The marginal probability can be described as

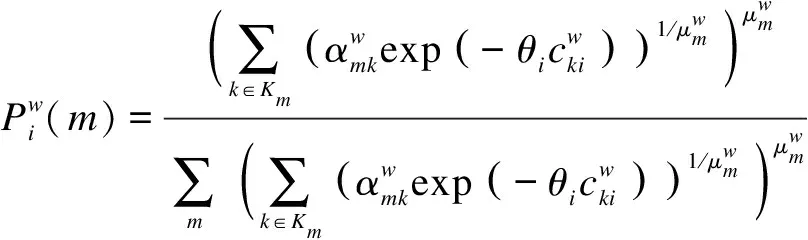
∀w,i,m

(3)

and the conditional probability may be given by the following equation:

(4)

2 Proposed Mathematical Model for the Modified GNL-SUE Model

2.1 Modified GNL-SUE model

The conventional GNL-SUE model is modified in this paper by incorporating the constraints of multiple user classes of GVs and BEVs and the distance limit of BEVs to handle the range anxiety and overlapping path issues jointly.To simplify the complexity of the modified GNL-SUE model, a series of assumptions are proposed:

1)The travel demand population includes only GV and BEV users.

2)The total travel demand for each type of vehicle at each origin is predetermined.

3)GV and BEV users have the same travel time on the same path.

4)Without loss of generality, all EVs are fully charged at their origins.

2.2 Proposed mathematical model

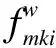
minZ=Z1+Z2+Z3

where

(5)

s.t.

(6)

(7)

(8)

(9)

(10)

Eq.(6)represents the flow conservation constraints; that is, the flow on all paths connecting each O-D pair must be equal to the O-D trip demand for user classi.Eq.(7)indicates that if the path length is less than or equal to the distance limit for a given user classi, then the flow on that path is positive; otherwise, the path flow should be equal to zero.Eq.(8)denotes the incidence relationship between link-path flows.Eq.(9)is a summation of the link flows of the user classi, while Eq.(10)is the flow of nonnegativity constraint.

2.3 Equivalence and uniqueness conditions

Proposition1The proposed mathematical model is equivalent to the modified GNL-SUE model with multiple user classes and distance limits.

ProofAny flow pattern obtained by solving Eqs.(5)to(10)is generally acknowledged to satisfy the SUE condition.The Lagrangian of the proposed mathematical model can be formulated as

(11)

The first-order conditions of the proposed mathematical model are equivalent to the first-order conditions of Lagrangian.Therefore, the following conditions must hold at the stationary point of the Lagrangian considering the path-flow variable, that is,

(12)

The partial derivatives ofL(f,μ,λ)considering the path-flow variable is then given by

(13)

L(f,μ,λ)must be minimized considering nonnegative path flows.Thus, the expression can be rewritten as

(14)

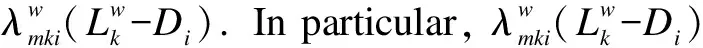
(15)

Submitting Eq.(15)into Eq.(14)and multiplying both sides byθi, the following is obtained:

(16)

(17)

Summing the above expression by pathk, the following is obtained:

(18)

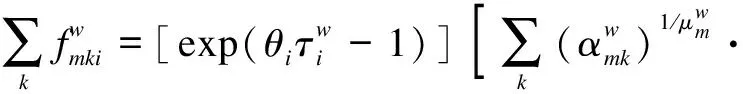
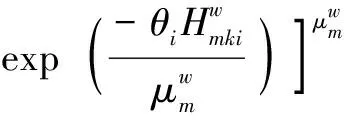
(19)

Summing Eq.(19)by link(nest)m,

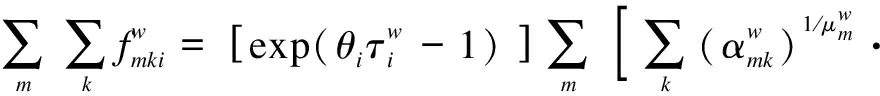
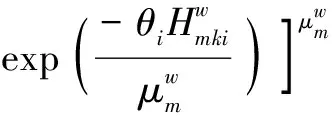
(20)

Dividing Eq.(19)by Eq.(20), the marginal probability that nestmwill be chosen is obtained as shown below.

(21)

Dividing Eq.(18)by Eq.(19),

(22)

Thus, the conditional probability of pathkwill be chosen in nestm.

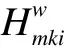
Proposition2The proposed mathematical model has a unique solution.

ProofDemonstrating that the Hessian matrix of the objective function of the proposed mathematical model is positive definite is sufficient to prove the uniqueness of the solution.The feasible region ofZ1is the same as Fisk’s formulation; thus, it is convex.The second derivative ofZ2andZ3can be calculated as follows:

(23)

(24)

2.4 MSA-based solution to the proposed mathematical model

The method of successive average(MSA)is adopted to solve the proposed mathematical model.The application steps of the MSA algorithm to solve the proposed mathematical model are presented below.

Step1Parameter settings.Determine a feasible path set.Meanwhile, set the distance limitDand the convergence toleranceε.

Step2Initialization.Calculate inclusion coefficientsαand nesting coefficientsμ.Find an initial path flowf(1).Set iteration countern=1.

Step3Update.Calculate the link flowx(n)based on the current path flowf(n).Update the link travel timec(x(n))and path travel timeT(n).

Step4Direction finding.Perform a stochastic network loading based on the current set of path travel timeT(n), yielding an auxiliary solutionY(n).

Step5Move.Setf(n+1)=f(n)+(1/n)(Y(n)-f(n)).Notably, the step size is the reciprocal of the number of iterations.

Step6Convergence test.If ‖f(n+1)-f(n)‖/‖f(n)‖≤ε, then stop; else, setn=n+1 and go to Step 3.

3 Numerical Examples

Two road networks are selected in this section for testing the purpose of this paper.Specifically, a small network containing overlapping and nonoverlapping paths is first selected to show the performance of the proposed mathematical model handling the overlapping path issue.The result indicates that the distance limit has an important impact on the path and link flows at equilibrium.The well-known Nguyen-Dupuis network is selected to demonstrate the performance of the proposed mathematical model handling the range anxiety issue by analyzing the effect of changes in distance limits on the path flows of GV and BEV.

3.1 Small network: Performance for overlapping path issue

The small network comprises 1 O-D pair, 5 links, and 3 paths, as shown in Fig.1.The total demand is equal to 1000.In addition, the BPR function is used to calculate link travel time, in which its coefficients are set toα=0.15 andβ=4.The distance limit of BEVs is set to 10 herein, and the distance limit of GVs is unlimited.The market share for GVs and BEVs is defined as 0.5 and 0.5,respectively.The dispersion parameters of GV and BEV users are respectively set to 0.3 and 0.5.The iteration accuracy of the MSA-based solution algorithm is defined asε=0.000 1.The free-flow travel time and capacity for each link on this small network are shown in Tab.1, and the path composition and length are exhibited in Tab.2.The values in Tabs.1 and 2 are adopted from Li et al[32].

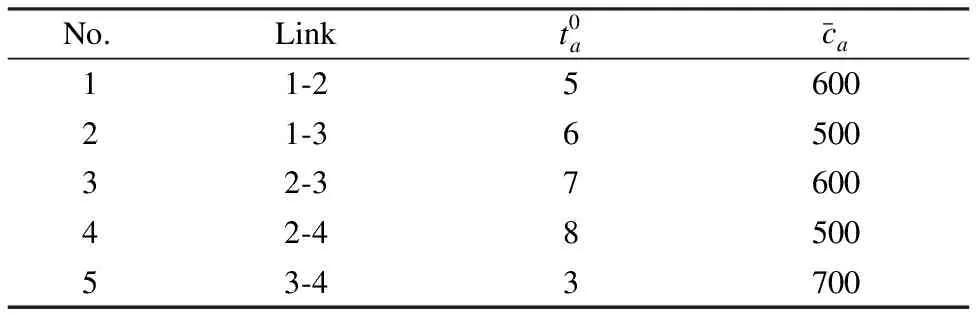
Tab.1 Link characteristics of the small network

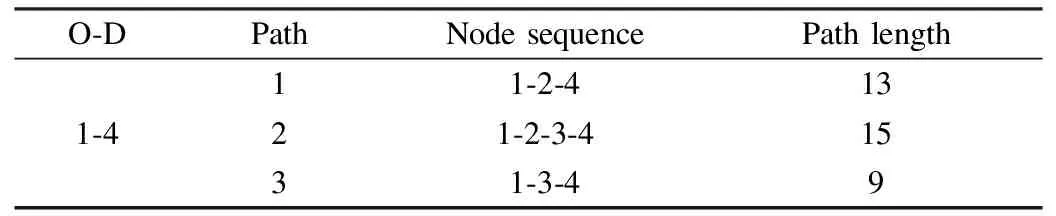
Tab.2 Path composition and path length

Fig.1 Small network

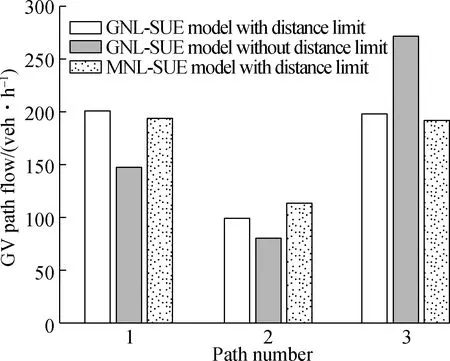
The path and link flows calculated by the proposed mathematical model(i.e., the GNL-SUE model with a distance limit), the GNL-SUE model without a distance limit, and the MNL-SUE model with a distance limit are also shown in Figs.2(a),(b), and(c), respectively.

Fig.2 shows that the path and link flows assigned by the proposed mathematical model are different from the GNL-SUE model without a distance limit and the MNL-SUE model with a distance limit.This difference is due to the consideration of the distance limit of the BEVs and the similarities between paths by the proposed model.More specifically, Figs.2(a)and(b)reveal the results of path flows assigned by the proposed mathematical model and the GNL-SUE model without a distance limit, wherein GV flow is assigned to paths 1, 2, and 3, while BEV flow is not assigned to paths 1 and 2.GV users are unaffected by the distance limit, while the length of paths 1 and 2 are greater than the distance limit of BEVs.Therefore, no BEV users travel on the two paths.

(a)

Additionally,Fig.2(c)shows that the link flows assigned by the proposed mathematical model on links 1 and 5 are smaller than those of the MNL-SUE model with a distance limit.Meanwhile, the link flows assigned by the proposed mathematical model on links 2 and 4 are larger than those of the MNL-SUE model with a distance limit.This finding is due to the MNL-SUE model with a distance limit, which does not consider the similarities between the paths.Therefore, the flows of the overlapping links are overestimated.By contrast, the proposed mathematical model overcomes the IIA drawback of the MNL-SUE model with a distance limit by considering the similarity among various paths.Therefore, the links with multiple overlapping paths are assigned fewer flows than the MNL-SUE model with a distance limit.

3.2 Nguyen-Dupuisnet work: Performance for range anxiety issues

The Nguyen-Dupuis network is selected to analyze the effect of the distance limit parameter on the path flows of GVs and BEVs.This network includes 4 O-D pairs, 13 nodes, 19 links, and 25 paths, as shown in Fig.3.The total demand for each O-D pair isq1-2=660,q1-3=495,q4-2=412.5, andq4-3=495.Other corresponding parameters are the same as those set in the small network.The free-flow travel time and capacity for each link on the Nguyen-Dupuis network are shown in Tab.3.The values in Tab.3 are adopted from Xu et al[36].The path composition and length are exhibited in Tab.4.The values in Tab.4 are adopted from Jiang et al[6].

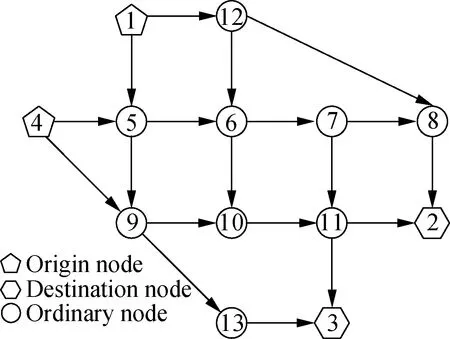
Fig.3 Nguyen-Dupuis network

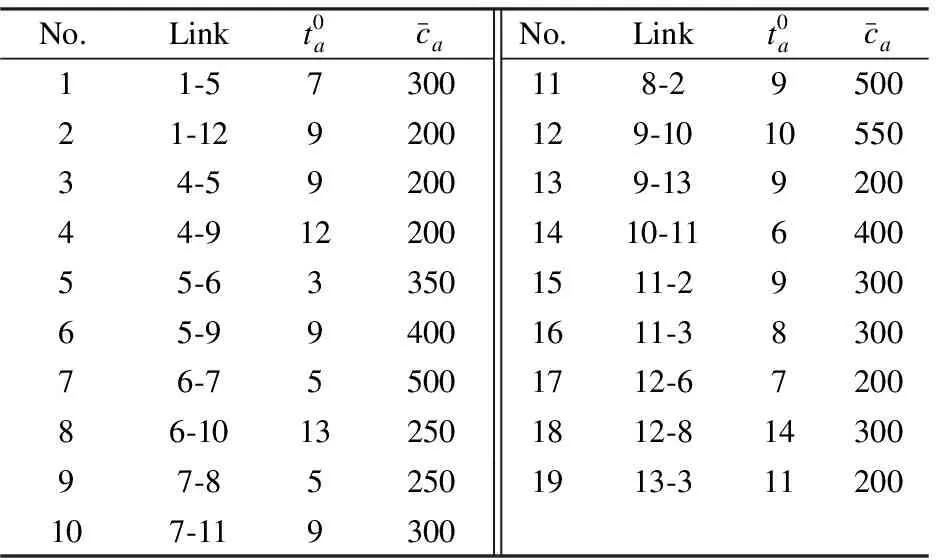
Tab.3 Link characteristics

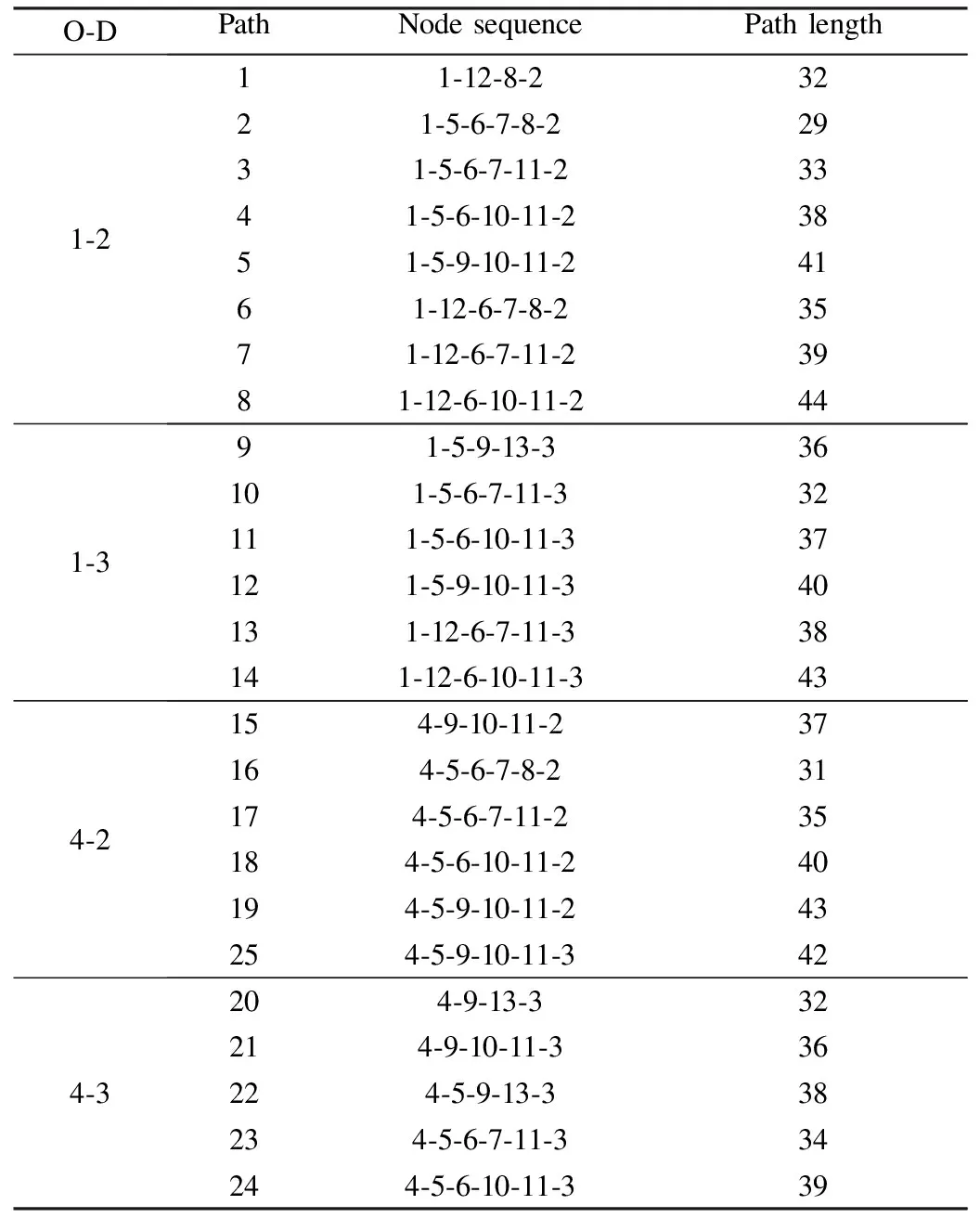
Tab.4 Path composition and path length

The variation of the path flows of GV and BEV with distance limits is depicted in Fig.4 to examine the impacts of the distance limit on the path flows of GV and BEV in each O-D pair.

Fig.4 shows that only 2 to 4 paths in each OD pair are available and carry BEV flows whenDtightens.BEV flows are assigned to additional paths due to the increase in the number of paths available whenDloosens, and the BEV flows gradually tend to stabilize.By contrast, the GV flows are assigned to each path in four O-D pairs because no distance limit exists.Moreover, the GV and BEV flows on some paths(e.g., paths 1, 10, 16, and 20)show opposite variations asDincreases.This phenomenon may be explained by the strong influence of distance limits on the route choice behavior of BEV users.In other words, BEV users are not allowed to travel on

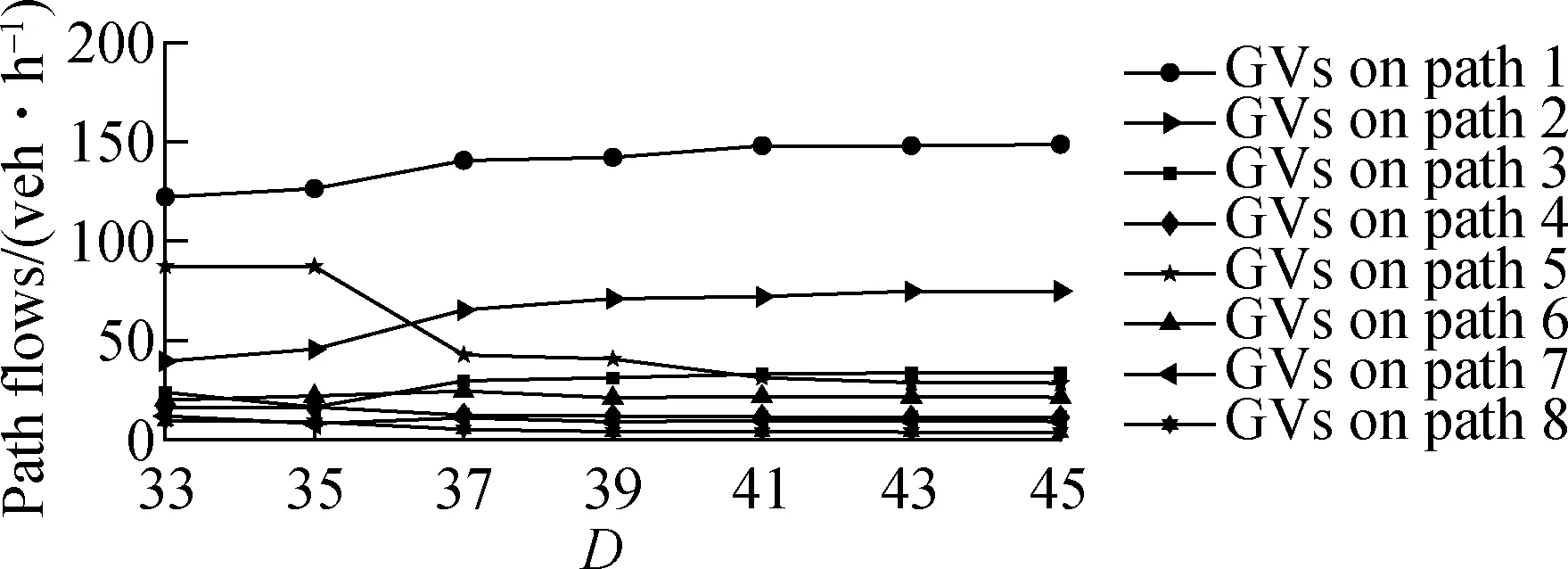
(a)

paths restricted by distance; thus, they tend to choose short paths to complete their trips.These short paths will then become oversaturated due to the entry of BEV users, which causes a significant decline in the capacity of the links contained in those paths and a substantial increase in path travel time.Therefore, GV users prefer to use these unsaturated paths to reduce their travel time.

4 Conclusions

1)A modified GNL-SUE model is proposed by incorporating the constraints of multiple user classes with distance limits on BEVs.An equivalent mathematical model and associated solutions were also provided for the proposed model.

2)The distance limit has an impact on the path and link flows at equilibrium, and the proposed mathematical model can overcome the IIA drawback of the MNL-SUE model with distance limits by handling the overlapping path issue.

3)Results using the Nguyen-Dupuis network show that the proposed approach can handle the range anxiety issue by selecting different distance limit parameters in traffic assignment.