Graph-enhanced neural interactive collaborative filtering

Xie Chengyan Dong Lu

(1School of Automation, Southeast University, Nanjing 210096, China)(2School of Cyber Science and Engineering, Southeast University, Nanjing 211189, China)

Abstract：To improve the training efficiency and recommendation accuracy in cold-start interactive recommendation systems, a new graph structure called item similarity graph is proposed on the basis of real data from a public dataset.The proposed graph is built from collaborative interactions and a deep reinforcement learning-based graph-enhanced neural interactive collaborative filtering(GE-ICF)model.The GE-ICF framework is developed with a deep reinforcement learning framework and comprises an embedding propagation layer designed with graph neural networks.Extensive experiments are conducted to investigate the efficiency of the proposed graph structure and the superiority of the proposed GE-ICF framework.Results show that in cold-start interactive recommendation systems, the proposed item similarity graph performs well in data relationship modeling, with the training efficiency showing significant improvement.The proposed GE-ICF framework also demonstrates superiority in decision modeling, thereby increasing the recommendation accuracy remarkably.

Key words：interactive recommendation systems; cold-start; graph neural network; deep reinforcement learning

Personalized recommendation systems have become ubiquitous in the information industry, and they have been applied to classic online services.Traditional recommendation systems have been widely studied under the assumption of a stationary environment, where user preferences are assumed to be static[1-2].However, such models fail to explore users’ interests when few reliable user-item interactions are provided, such as that in a cold-start scenario.They also fail to model the dynamics of user preferences, thus leading to poor performance.Therefore, the research into interactive recommendation systems(IRSs)has flourished in recent years.IRSs consider recommendations as sequential interactions between systems and users.The main idea in modeling IRSs is to capture the dynamic nature of user preferences and achieve optimal recommendations in a time periodT[3].IRS research has two directions: contextual bandit and reinforcement learning(RL).Although contextual bandit algorithms have been used in different recommendation scenes, such as collaborative filtering[4-5]and e-commerce recommendation[6], they are usually invalid in nonlinear models and demonstrate too much pessimism toward recommendations.RL is a suitable learning framework for interactive recommendation tasks as it does not suffer from such issues.In the study of applying RL to IRSs, the themes include large action spaces, off-policy training[7-8], and online model framework[9].

The interactive recommendation problem in the current study is set in a cold-start scenario, which provides nothing about items or users other than insufficient observations of user-item ratings.A deep RL framework[10], which can be regarded as a generalized neural Q-network, is adopted to tackle the above problem.As for the representation of items, an embedding lookup tableX∈RN×deis adopted, with each itemebeing represented as a vectorxe∈Rde.The embedding lookup table is trained end to end in the framework.However, because such an embedding layer is optimized by user-item interactions in interactive recommendations and lacks an explicit encoding of crucial collaborative signals, an item similarity graph is proposed, and an embedding propagation layer constructed by graph neural networks(GNNs)is devised in this work to refine items’ embeddings by aggregating the embeddings of similar items.

Given the graph structure from the data in recommendation systems, designing a proper graph and utilizing GNNs in recommendation systems are appealing.

User-item bipartite graphs are constructed in traditional recommendation methods for improved performance in rating prediction tasks[11], while sequence graphs are transformed in sequential recommendation methods to capture sequential knowledge[12].Knowledge graphs[13]are utilized for additional information.By introducing an item similarity bipartite graph in the recommendation framework, we make interactive recommendations effective because of the deep exploitation in structural item similarity information inferred from user-item interactions.A user-item bipartite graph is suggested in the RL framework for interactive recommendations[14].

In sum, a new graph called an item similarity graph is built in this study to alleviate the computational burden while showing comparative structural information as a user-item bipartite graph.Then, a graph-enhanced neural interactive collaborative filtering(GE-ICF)framework, which devises an embedding propagation layer into an RL framework, is proposed for interactive recommendation tasks.Empirical studies on a real-world benchmark dataset are conducted, and the results show that the proposed GE-ICF framework outperforms baseline methods.

1 GE-ICF Framework’s Method

1.1 Preliminaries

A typical recommendation system has a set ofmusersU={1, 2, …,m} andnitemsI={1, 2, …,n} with an observed feedback matrixY∈Rm×n, whereyijrepresents the feedback from userito itemj.Here feedback can be explicit(e.g., rating, like/dislike choice)or be implicitly inferred from watching time, clicks, reviews, etc.For cold-start users in this study, an interactive recommendation process is conducted in a time periodTbetween the recommender agent and a certain user.At each time steptin the interaction time period {0, 1, 2, …,T}, the recommendation agent calculates itemitto be recommended by policyπ:st→Iand suggests it to certain useru, wherestrepresents the user state at time stept.Then, the user gives feedbackyu,iton the recommended item to the recommender agent, and this feedback guides the agent in updating the user’s state and making next-round recommendations.The goal of designing an interactive recommendation system is to design a policyπthat maximizesGπ(T)as

(1)

whereGπ(T)is the expected cumulative feedback in a time periodT.Although exploiting the user state at the current time step facilitates the derivation of accurate recommendations and maximization of immediate user feedbackyu,it, the exploration of items for recommendation is necessary for completing user profiles and maximizing cumulative user feedbackG(T), which is regarded as the delayed reward for a recommendation.RL is a sequential decision learning framework that is aimed at maximizing the sum of delayed rewards from an overall aspect[10].Therefore, RL is applied in our system to balance exploitation and exploration during interactive recommendations.

The essential underlying model of RL is a Markov decision process(MDP).An MDP occurs between agents and the environment.In this study, the agent is the proposed recommendation system, and the environment is equivalent to the users of the system, as well as all the movies recorded in the system.The MDP is defined with five factors(S,A,P,D,γ).These factors are introduced and instantiated in the IRS for cold-start users.Fig.1 illustrates the interactive recommendation in the MDP formulation.

Fig.1 Interactive recommendation process in MDP formulation

State spaceScontains a set of statesst.In this study, a state at timet:st={i0,yu,i0,…,it-1,yu,it-1} denotes the browsing history and corresponding feedback of a userubefore timet.To reflect the change of user interests with time, the items instare sorted in chronological order.

Action spaceAis equivalent to item setIin a recommendation.An action at timet:at∈Adenotes the item recommended to a user by the recommender system according to current user statest.

RewardDis a set the recommender system receives depending on user feedback.

Feedbackyu,iton the recommended itemitis returned by useru, and it may be explicit or implicit depending on certain systems.The recommendation system receives immediate rewardrst,ataccording to the feedback.Rewards may not be the same as feedback; that is, reward shaping technology may be used to improve algorithm performance.

Transition probabilityp(st+1|st,at)defines the probability of state transition fromsttost+1after an item is recommended as an action.An MDP is assumed to have a Markov property; that is, it satisfiesp(st+1|st,at,…,s1,a1)=p(st+1|st,at).p(st+1|st,at)= 1 is set at any time step, which means that the state at the next time stept+1 is determined once statestand actionatare fixed.In this work, the state att+1 is updated by appending actionatand corresponding feedbackyu,itto statest; that is, it is accumulative.

Discount factorγ∈[0,1]defines the discount factor measuring the importance of future reward in the present state value.Specifically,γ=0 means that the recommender agent only considers the immediate reward whileγ=1 means that all future rewards are thought to be as important as the immediate reward.

Solving the RL task is to find an optimal policyπθ:SAthat maximizes the expected cumulative rewards from a global view.The expected cumulative rewards can be presented by a value functionNote thatEπθis the expectation under policyπθ,tis the current time step, andrt+kpresents the immediate reward at a future time stept+k.A variant of neural networkQ(s,a;θ)(i.e., Q-network)[15]is adopted to estimate the policyπθ.A Q-network adopts the experience replay mechanism and a periodically updated target network to ensure the coverage of the model.A finite-size memory called a replay buffer is applied, and transition samples represented by(st,at,rt,st+1)are stored there for sampling and model training.

In the recommendation procedure,the state space and action space are represented by item vectors.In practice, building item vectors by one-hot encoding is not efficient enough because of the one-hot encoding’s extremely high dimension and sparsity, especially in problems with a large action space.Instead, we train dense, low-item vectors end to end in the RL framework.GNNs are integrated into the embedding process because of their superiority in representation learning.

1.2 Item similarity bipartite graph construction

Although a user-item interaction bipartite graph is widely used in collaborative filtering, it suffers from huge data size and a high calculational burden.Therefore, we propose to build an item similarity bipartite graph with the assumption that a user’s interest does not change frequently.On the basis of this assumption, we count the frequency of two items simultaneously existing in one user’s history.Assume that two items exist in n users’ histories; they are thought to be similar ifn≥g, wheregdenotes an item similarity coefficient.An edge exists between two similar item nodes in the item similarity graph.We set all edges to have equal weights initially and learn the contribution of each neighbor to central nodes with an attention network.A toy sample of a user-item interaction bipartite graph and an item similarity bipartite graph is illustrated in Fig.2.

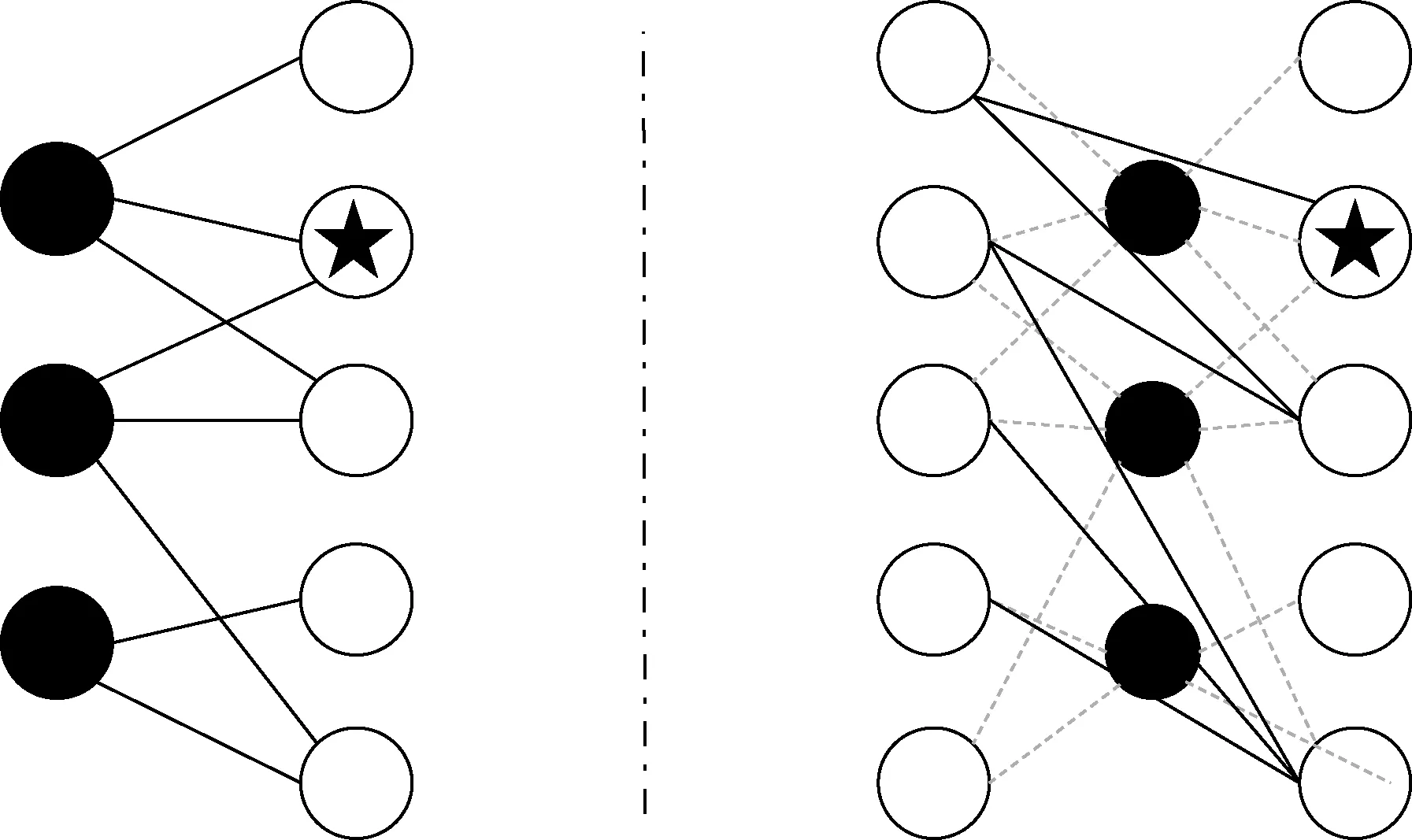
Fig.2 Illustration of a user-item interaction bipartite graph and an item similarity bipartite graph.(a)User-item interaction bipartite graph;(b)Item similarity bipartite graph

Through the design of the item similarity graph, structural information among items is modeled with the graph size sharply decreasing because user nodes are no longer built in it.

1.3 Model architecture

We now present details of the proposed GE-ICF framework, the architecture of which is illustrated in Fig.3.The framework is structured with four components: 1)an embedding layer that initializes all item embeddings in the system; 2)an embedding propagation layer that refines the item embeddings by injecting structural item similarity relations; 3)a stacking self-attention block that takes item embeddings and a user’s corresponding feedback as input to generate a user profile; 4)a policy layer that predicts the most preferable item for the user.The framework is trained end to end with Q-learning[15].

Fig.3 Architecture of the GE-ICF framework

1.3.1 Embedding layer

Given a user statest={i0,yu,i0,…,it-1,yu,it-1}, we first represent itemsitwith embedding vectors.We build an embedding lookup tableX∈RN×defor the initialization of allNitems’ embeddings in the system, withdedenoting the embedding size.The embedding lookup table is initialized randomly and optimized in an end-to-end style.In contrast to traditional collaborative filtering methods, which take these ID embeddings as items’ final embeddings, they are refined by propagating the information of similar items on an item similarity graph in the GE-ICF framework, thus leading to effective item representations.

1.3.2 Embedding propagation layer

We develop an embedding propagation layer from the idea of GAT.This layer aims to aggregate similar items’ features to refine the central nodes’ embedding vectors.It takes the embedding lookup tableX∈RN×deand item similarity bipartite graph as input and outputs a graph-aware embedding lookup tableX′∈RN×d′e, thus transforming an itemi’s embedding vector fromxi∈Rdetox′i∈Rd′e.

A shared weight matrixW∈Rde×d′eis necessary in the first step for transforming inputted embedding vectors into high-order features.This step allows the framework to obtain sufficient expressive power.Then, an attention mechanism attention:Rd′e×Rd′e→Ris adopted to measure different importance levels of neighbor nodes for central nodes in the form of attention coefficients:

eij=attention(Wxi,Wxj)

(2)

whereeijis an attention coefficient calculated to measure the contribution of a neighbor nodej∈Nifor the central nodeicentralandNidenotes all the one-hop neighbors of nodeicentralin the graph as well as the nodeicentralitself.A softmax function is then applied to all attention coefficientsei*as

(3)

whereαijis a normalized attention coefficient that makes all the importance levels of nodes inNicomparable.

We adopt a single-layer feed forward neural network for the attention mechanism, in which the normalized attention coefficient can be expanded as

αij=softmaxj(eij)=

(4)

whereaT∈R2×d′eis a parameter vector for linear transformation;‖ is the concatenation operation; LeakyReLU(·)is a function for nonlinearity modeling.

As the central nodeicentralis already contained in the node setNi, the message propagation process and the message aggregation process can be regarded to be conducted simultaneously by a linear combination of the features corresponding to related nodes and the nonlinearity transformation on the combined embedding vector:

(5)

wherex′iis a graph-aware embedding vector of itemicentral.

We employ multihead attention to stabilize the learning process of self-attention.The final item vectors can be represented by the concatenation or average ofKindependent attention outputs.We find that concatenation is more sensible to capture graph-aware item representations in this work:

(6)

wherekis the serial number of each attention head.

1.3.3 Stacking self-attention block

A user profile is then generated by stacking self-attention blocks with user history and the corresponding feedback, and user history is represented with refined item embeddings.

The numbers of items with different user feedback items in a user’s history show extreme imbalance; that is, positive feedback items are much fewer than negative feedback items with the assumption that unexposed items are negative samples for users.As we use a dataset within an explicit rating in this work, the items in user history are classified with ratingsyu,itin user state, and different rated items are processed independently by stacked self-attentive neural networks[10].

1.3.4 Policy layer

With the generated user profile, we apply a two-layerperceptron(MLP)to extract useful information and model corresponding action-value functionQθ(st,·)for all items under the current state:

(7)

whereutis the user profile vector at timestampt;W(1)，W(2)are the weight matrixes of each perceptron layer;b(1),b(2)are the biases of each perceptron layer; ReLU(·)is a function for nonlinearity modeling.

The policyπθ(st)is to recommend itemiwith maximal Q-value for useruat timet:

πθ(st)=argmaxiQθ(st,i)

(8)

1.4 Model training

We utilize Q-learning[15]to train the whole GE-ICF framework(see Fig.3).The adopted datasets are divided into training setΓtrainand test setΓtestby users.Before the interaction, an item similarity graph is constructed with training users’ interactive dataΓtrainand item similarity coefficient g and is applied to the framework.In thet-th trial, a user statest={i0,yu,i0,…,it-1,yu,it-1} is observed, and the item with the largest value calculated by the approximated value functionQθ(st,·)is chosen as corresponding recommendationit.Theζ-greedy policy is used for exploration during training to enrich the learning samples.Then, the recommender agent receives the user’s feedbackyu,itonitand maps it into rewardrst,it.At the same time, the user state is updated intost+1={i0,yu,i0,…,it,yu,it}.Therefore, a new transition sample(st,it,rst,it,st+1)is generated and stored in the memory buffer for batch learning.

We train the weights in the framework in each episode by minimizing the mean squared error:

error(θ)=E(st,it,ru,it,st+1)～M[(yt-Qθ(st,it))2]

(9)

where

(10)

is the target value from the optimized Bellman equation, and the target network[15]is applied to improve system robustness.γis a discount factor, andQθ-(st+1,it+1)is theQ-value calculated by the target network.Efficient learning is adopted[10]in this study, withγset to be dynamic for improved model training.Mis a transition sample set stored in the memory buffer.

2 Experiments

We conduct extensive experiments to answer the following questions:

1)Does the application of GNNs refine the item embeddings and improve the recommendation efficiency?

2)Does the designed item similarity graph achieve comparable results to user-item bipartite graphs while sharply decreasing training time?

3)How does the depth of GNNs influence the final recommendation efficiency?

The experimental settings are reviewed first in the following subsection.Thereafter, the questions are discussed in the Results and Analysis section.

2.1 Experimental setting

2.1.1 Datasets

Experiments on recommendation systems should be conducted online to determine their interactive performance.However, online experiments are not always possible as they require a platform and could possibly sacrifice user experience.Therefore, a stable benchmark dataset, MovieLens 100K, is adopted for the experiment in this work.The statistics of the dataset are summarized in Tab.1.

Tab.1 Summary statistics of datasets

To make the experiments reasonable, we assume that each item in a user’s history in the dataset is the user’s instinctive action and is not biased by recommendations.In addition, the ratings from users for items not in their records are assumed to be 0 following existing studies.

2.1.2 Comparison methods

To verify the efficiency of our proposed GE-ICF framework, we select five baselines among different types of recommendations for comparison.

1)Random:A policy uniformly samples items to recommend to users.It is a baseline to output the worst performance, in which no algorithms are used for recommendations.

2)Popular: An algorithm that orders items with the number of ratings and recommends items accordingly.Before the popularity of personalized recommendations, Popular was a most widely adopted policy because of its surprisingly excellent performance on recommendations.

3)Thompson sampling(TS)[5]: An interactive collaborative filtering algorithm achieved with the combination of probabilistic matrix factorization(PMF)and Thompson sampling.Thompson sampling can be replaced with other exploration techniques, such as GLM-UCB.We choose PMF with Thompson sampling as a representation of such techniques to compare it with our algorithm with the goal of balancing exploitation and exploration in recommendations.

4)NICF[10]: A state-of-the-art algorithm that applies RL to interactive collaborative filtering.We refer to its idea on the construction of the DQN-based framework and compare our work with it to verify whether the devised GNNs make sense.

5)GCQN[14]: A DQN-based recommendation that applies a user-item bipartite graph to detect the collaborative signal and uses GRU layers to generate the user profile.

6)GE-ICF:The proposed approach to the interactive recommendation with the item similarity bipartite graph devised.

7)GE-ICF-β: The same architecture as the GE-ICF, except that a user-item bipartite graph is devised in the framework.

We compare GE-ICF and GE-ICF-βto investigate whether the proposed item similarity graph achieves comparable performance in abstracting collaborative signals with the user-item bipartite graph while sharply reducing the burden on calculation.

We adopt cumulative precision duringTinteractionspTto evaluate the accuracy of recommendations:

(11)

wherebtis a parameter indicating whether the recommendation is satisfiable or not andnusersis the number of users.bt=1 ifyu,it≥4, and 0 otherwise.As we set the rewardrst,itunder the same rule, the cumulative precision is equivalent to the cumulative reward inTinteractions.

The dataset is divided into three disjoint sets by users: 85% of the users and their interactions are set as a training set, 5% of the users and their interactions comprise the validation set, and the remaining 10% of the users are set as the test set.In our approach, the batch size of learning is set to be 128, and the learning rate is fixed to 0.001.The memory buffer to replay training samples is set as large as 1×106for sufficient learning, and the exploration factorζdecays from 1 to 0 during training.The optimizer is chosen to be the Adam optimizer.The item similarity coefficientgis set to be 10.The experiments are conducted on the same machine with a 4-core 8-thread CPU(i5-8300h, 2.30 GHz), Nvidia GeForce GTX 1050 Ti GPU, and 64 GB RAM.We run each model separately five times under five different seeds and average the outputs for the final results.

2.2 Results and analysis

2.2.1 Influence of GNNs

The results ofpTover different models on the dataset MovieLens 100K are reported in Tab.2, whereT=10, 20, 40.

Tab.2 pT of different models on MovieLens 100K

We compare our proposed framework with five baselines and find that whenT=10, 20, and 40, the proposed framework remarkably outperforms the other baselines in terms of recommendation accuracy.This result verifies that the embedding propagation layer we proposed indeed improves the model’s capability of detecting collaborative signals and improves the recommendation accuracy in a cold-start scenario.

2.2.2 Efficiency of the proposed item similarity graph

The algorithms GE-ICF and GE-ICF-βare further compared onpTand seconds per training step(SPT)withT=40 in Tab.3.Although the precision of GE-ICF-βis slightly higher than that of GE-ICF whenTis small, the training time of GE-ICF-βis more than one and a half times as long as that of GE-ICF.This result means that the item similarity bipartite graph achieves comparable results to user-item bipartite graphs while the training efficiency is improved remarkably.

Tab.3 Performance comparison between GE-ICF and GE-ICF-β on MovieLens 100K

2.2.3 Influence of GNN depth

To investigate the influence of the GNN layers in the proposed framework, we vary the depths of the GNN layers in the range of {1, 2, 3}.Tab.4 summarizes the experimental results, and the results of the framework without GNN layers are presented for reference.

Tab.4 pT of the GE-ICF framework with different GNN depths on dataset MovieLens 100K

The results in Fig.4 indicate that although the application of GNN layers improves the recommendation precis-ion during time periodT, the recommendation performance worsens as the depth of the GNN layers increases.p10achieves the best performance when the GNN layer depth is equal to 1, and the GE-ICF framework with two GNN layers works the best in the time periodT=20, 40.When the layer depth is up to 3, the recommendation efficiency decreases more sharply, even becoming worse than that of the framework without GNN layers.The reason might be that applying an excessively deep architecture would introduce noise to representation learning.Moreover, the multistacking of GNN layers might bring about an over smoothness issue.

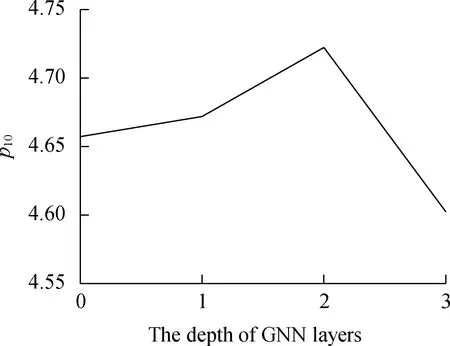
(a)

3 Conclusions

1)A GE-ICF framework is proposed in this work to enhance neural interactive filtering performance by recommending GNNs to capture collaborative signals.Extensive experiments are conducted on a benchmark dataset in this work.The results indicate that the recommended GNNs indeed make sense for the training of item embeddings and that the proposed GE-ICF framework outperforms others in interactive recommendation tasks.

2)The proposed item similarity graph is of great significance because it contains as much collaborative information as user-item bipartite graphs while sharply decreasing graph size and shortening training time.

3)Our future work involves several possible directions.Firstly, we would like to investigate how to extend the model by incorporating rich user information(e.g., age, gender, nationality, occupation)and context information(e.g., location, dwell time, device)in a heuristic way.Secondly, we are interested in the effective utilization of RL in IRSs under the guidance of the diversity of recommendations, which is the key indicator of model exploration degree.