小学数学数形结合思想方法的实践与思考

杨松军

数形结合思想是现阶段数学教学中的重要内容，对学生成绩层面的提升和课堂效率的提高起着积极的作用。小学数学中的数形结合理念，说的其实就是最为基础的数形模式，只有将其应用至数学教学中，才可以使学生拥有具备逻辑性特征的数学思维。在小学数学教学中，数形结合的理念和策略，指向数和图形之间的关系变换。学生在处理题目的过程中，会根据题目中所给予的已知要求，将图形问题变换为数量问题，或将数量问题转变为图形问题，以此降低题目的繁杂性。学生也可以借用简易化的方法，对复杂的问题进行解答。由于新课程改革在小学数学教学中的推行和落实，小学数学教师需要转变之前单一化的教学方式，将多元化的教学方式应用至课堂之中，进而提高学生学习数学的积极性，启发学生的活跃性思维，加强学生的课堂参与性，发挥学生的想象能力，推动学生的综合发展。

一、数形结合的概念阐述

在数学学科中，数和形是其中两个最古老也最基础的探究对象，它们在特定要求下，能够互相变换。小学数学研究的对象能够分成数和形两大部分。数和形之间有着紧密的关联，这种关联，就被称作数形结合或形数结合。身为数学学科中的一种基础思想和方法，应用数形结合的情况大致分为两种：其一，依托数的精准性，解读和明晰形的某些特性。其二，通过形的几何直观性，解读和明确数之间的某种关联。简言之，数形结合包含两个层面，即以数解形方面及以形解数方面。在借助数解答形的时候，部分图形会偏简单化，通过直接观察，是无法获取规律特性的，此时，就需要给图形赋予对应的数值，像边长、度数等。

从基本思想出发，数形结合思想指的其实就是数与形之间的对应关系，数形结合就是将抽象化的数学语言、数量关系、位置关系和几何图形联系起来，借助以数解形及以形解数，将复杂问题简易化、抽象问题具象化，进而完成简化解题路径的目标。

二、思考小学数学教学中应用数形结合思想的重要性

（一）应用数形结合思想的重要作用

1.满足小学生的思维发展特点

在小学时期，学生在思维能力层面的应用，多以形象思维为主。而图形、图画等形象类表达方式具备更好的认知成效、记忆成效和理解成效。与之对应的，这一时期的学生对抽象思维，像文字性理解、数字性理解等具备对应的认知难度。所以，在小学数学教学中，应用数形结合思想，可以把抽象思维和形象思维整合起来，依托形象化的表述形式，协助学生掌握和内化抽象化的数学内容，比如，在解决抽象数学问题的时候，应用图形，可以将其转化为简易化的数学问题，降低难度，提高解题的正确率。由此可见，数形结合的教学形式，更加适应小学时期学生思维发展的特性，适合学生的数学学习规律，有助于提高学生的认知能力、理解能力及解题能力。

2.激发小学生学习数学的兴趣

对小学时期的学生来说，学习数学的兴趣是其提高自身数学素养的内在动力，所以，教师要根据教材内容，依托学生的年龄特征和认知规律，开展趣味化的课堂活动教学，以此在教学的过程中，掌握学生的兴趣点，进而利用学生的认知和兴趣，对学生进行知识掌握层面的引导，促使学生敢于尝试在学习数学的过程中应用丰富的图形和图画等内容，并让学生依托图画和图形，感知到数学知识的内涵和魅力，使学生在主动探究的过程中，提高自身学习数学的积极性。

（二）应用数形结合思想的价值展现

1.可以直观抽象化的数学知识

在小学数学的实践教学过程中，教师面对的最大困境，就是无法把教材上难以理解的数学知识变得直观。比如，教师在讲述“分数概念和性质”的时候，若只是简单地进行文字叙述，其展现出的抽象性，会阻碍学生对数学知识的理解。但依靠数形结合思想进行实践教学，就能够依靠直观化的图形，向学生展示分数的概念。学生也能够透过数形结合，掌握分数的概念。

2.可以具象隐性化的数学规律

在小学数学的教学过程中，存在部分隐藏的数学规律，一些数学基础不牢、对教材知识掌握不扎实的小学生，可能就无法理解这些数学知识。因此，为了让这些抽象的数学规律更容易被小学生所接纳和内化，可以科学应用数形结合思想。比如，教师在讲述“位置和方向”的时候，可以结合具体化的建筑事物，向学生直观展现立体的建筑事物，在建筑的周围，标注上东南西北。学生能够透过不同建筑物之间的方向和定位，理解方向和位置的概念。

3.可以降低复杂数学知识的难度

三、在小学数学教学中融合数形结合思想的有效策略

（一）在概念讲解的过程中应用数形结合思想方法

1.课堂讲解

在数学教学的过程中，概念是所有知识的本源，也是学习的基础。但在传统的概念教学过程中，教师常用“说教”的形式，使得学生感到数学课堂的枯燥性，而降低自身学习数学知识的兴趣。从整体学生的角度出发，这种教学方式，导致学生的参与程度比较低。但数形结合思想的融合，可以改变这样的情况，教师能够借助直观图形的导入，帮助学生理解抽象化的概念，使抽象往具象转变，从而提高学生的逻辑推理能力，加强学生的数学抽象思想，深化学生的直观想象能力。

2.解析应用

数学学科具备一定的应用性，而对知识的现实应用是学科教育的最终目标。简单地说，在讲述概念的过程中，教师除了要幫助学生理解和内化抽象的概念，还要使学生基于自身的基础知识和解析能力，灵活应用已知的公式和运算内容。在深化学生的认知规律和理解能力的进程中，教师也能够融入数形结合思想，依托数形结合的教学方式，推动学生对概念的应用，进而完成熟练应用，提高解析能力的目标。

以小学数学北师大版教材六年级下册第一章“圆柱与圆锥”为例。教师在讲述这节课的时候，要以形助数，让学生直观感知立体化和三视化的图形，以此了解公式形成的起源与过程。学生可以在形的推进下，明确公式的具体应用，以此提高自身综合素养。教师可以结合小学数学课堂上圆柱与圆锥的体积计算公式与图形的变化，利用微课视频展现给学生，这样能够帮助学生更好地对数形结合概念有一定的了解。

（二）在计算教学的过程中应用数形结合思想方法

1.算理讲述

“算理”指的其实就是在运算题目进程中所展现出的道理，事实上，学生对概念的现实应用，实则就是对计算理念的现实应用。比如，在计算188+92的时候，依照数的构成，学生可以这样分析：188由1个百、8个十、8个一构成，92由9个十、2个一构成，在这之后，百位数和百位数相加，十位数和十位数相加，一位数和一位数相加，若需要进位，那就进位，最终得出280，这其实就是计算理念。但不少学生并不了解计算理念，常常直接依靠进位法进行运算，导致出现不少运算层面的错误。因此，在计算理念的教学过程中，教师可以渗透数形结合思想，协助学生了解计算理念的本质，加强学生对已知内容的应用水平。比如，一百可以用圆形代替，十可以用长方形代替，一用三角形代替，这样数的加减就可以通过图形表示，帮助学生有更深刻的理解和认知。

2.找寻规律

对规律的找寻，也是融合数形结合思想的高效策略。在加強学生逻辑思维能力的过程中，教师要提高学生的分析能力，让学生在探究和解析的过程中，提高自身的思维，从而加强学生的问题解答能力。而在渗透数形结合思想的过程里，教师要结合教材上的图形规律例题，活跃学生的思维，提高学生的分析能力。

例如图1，方框内的点群包含多少个点？第（10）个点群包含多少个点？前10个点群中，所有点的总数是多少？

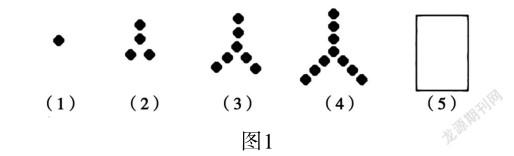
关于这类规律题，教师首先要带领学生解析图形，找寻到图形和图形之间的变化规律，比如，第（1）个点群包含1个点，第（2）个点群包含4个点，第（3）个点群包含7个点，第（4）个点群包含10个点。之后，教师可以使学生动手绘制图形，找出第（5）个和第（6）个点群包含多少个点。学生可以得出第（5）个点群包含13个点，第（6）个点群包含16个点，最后教师发挥引导作用，促使学生把所获取的结果整合起来，比如， 1，4，7，10，13，16……这样就可以将问题变换为数量问题，学生就可以简单得出答案。在找寻规律的过程中，教师要提高学生的主体地位，使其发挥主体价值，激励学生进行独立化思考，这样不仅可以保证数形结合得到融合，而且对学生素养的提升和思维的进展，都有相应的推动作用。

（三）在应用题的教学过程中应用数形结合思想方法

小学时期的应用题有很多类型，教师可以依靠应用题的类型，将其分解，像相遇问题、速度问题、追寻问题等，而在解析应用题的时候，教师和学生也能够依托数形结合思想，找寻题目中的已知数量和等量关系。在讲述这些应用题的时候，教师要延展自身的引导能力，使学生进入到问题解析的过程中，使学生梳理清楚数量之间的联系，继而明确解题路径，提高解题的正确率。

以“相遇问题”为例：佳佳和芳芳在一条马路的两端相向而行，佳佳每分钟走60米，芳芳每分钟走80米，他们同时出发，5分钟之后遇到了，这条马路长多少米？

在解析此题的时候，教师可以引导学生根据题目中的已知数据，建立数轴，将文字问题图像化，将抽象问题具象化，进而解出答案。

依靠简单化的图形分析，学生可以较快速地找寻到应用题中的数量关系。当然，这样的解题过程，离不开学生对数形结合思想的应用，这些内容能够让学生认知到数形结合思想的作用。除了这种类型题目中的数形结合，其他类型的题目，也可以应用数形结合思想和方法。单纯地围绕着理论描述，无法明确具体的过程，可能会出现计算错误的问题。简单地说，教师可以依靠应用题的讲述过程，渗透数形结合思想，使学生知道如何应用数形结合，明确数形结合思想所带来的价值，进一步提升自身的解题能力和逻辑思维能力。

了解了小学数学中数形结合思想教学的情况，教师需要认识到在小学数学中展开数形结合思想教学的时候，一定要把握学生的实际。借助新媒体，将图形更加生动地展现出来，通过数形结合，让学生的数学思维得到发展和提升。与此同时，小学阶段学生的学习能力各不相同，所以教师要采取分层化理念，将数形结合思想教学应用其中，围绕不同学生的思想认知，利用不同的数形结合形式，帮助学生对此有深刻的了解。