载荷冲击时歪斜滚子副的动态润滑问题研究

2022-07-12杨苗苗范丽丽张婷婷

常州工学院学报 2022年3期

杨苗苗，范丽丽，张婷婷

(滁州职业技术学院机械与汽车工程学院，安徽滁州 239000)

轴承在各类机器设备中应用广泛，是最易破损的常见元件之一[1]。轴承的功能、稳定性和可靠性等很大程度上决定着主机的使用寿命。滚动轴承因其使用广泛是轴承中最为常见的类型之一，而其滚子的歪斜现象是最常见的现象之一。原因如下：①滚子本身的几何形状差异、轴和定位装置的形变，均可导致轴承滚子的歪斜；②当轴承滚子同时承受径向和轴向的交变负荷时，在轴承内外圈挡边的干涉下迫使滚子产生歪斜现象。

滚子长期在歪斜非正常状态下运行，极速加剧了滚道与滚子间的磨损，并产生大量热量致使润滑剂和防锈剂分解，极大缩短了轴承实际运行寿命[2]。众多国内外顶尖专家对此进行了大量研究。代小娟[3]对各种尺寸和类型的轴承进行摩擦力矩试验；Yang等[4]使用有限元法对推力滚子轴承接触问题进行分析，并在试验的基础上提出了向心和推力滚针轴承摩擦力矩的经验计算公式；Harris[5]于20世纪70年代提出了歪斜滚子压力计算方法。外界工况的瞬时改变都会对油膜的动态稳定效应产生影响。因此，对轴承滚子非稳态油膜润滑问题的探讨显得十分必要。

1 模型及数值计算

1.1 模型

图1(a)、(b)分别为非歪斜滚子和歪斜滚子与轴承外圈接触分布示意图。图1(b)所示的θ角即为滚子歪斜角。

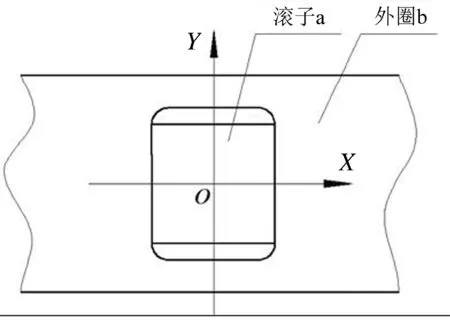
(a) 正常接触

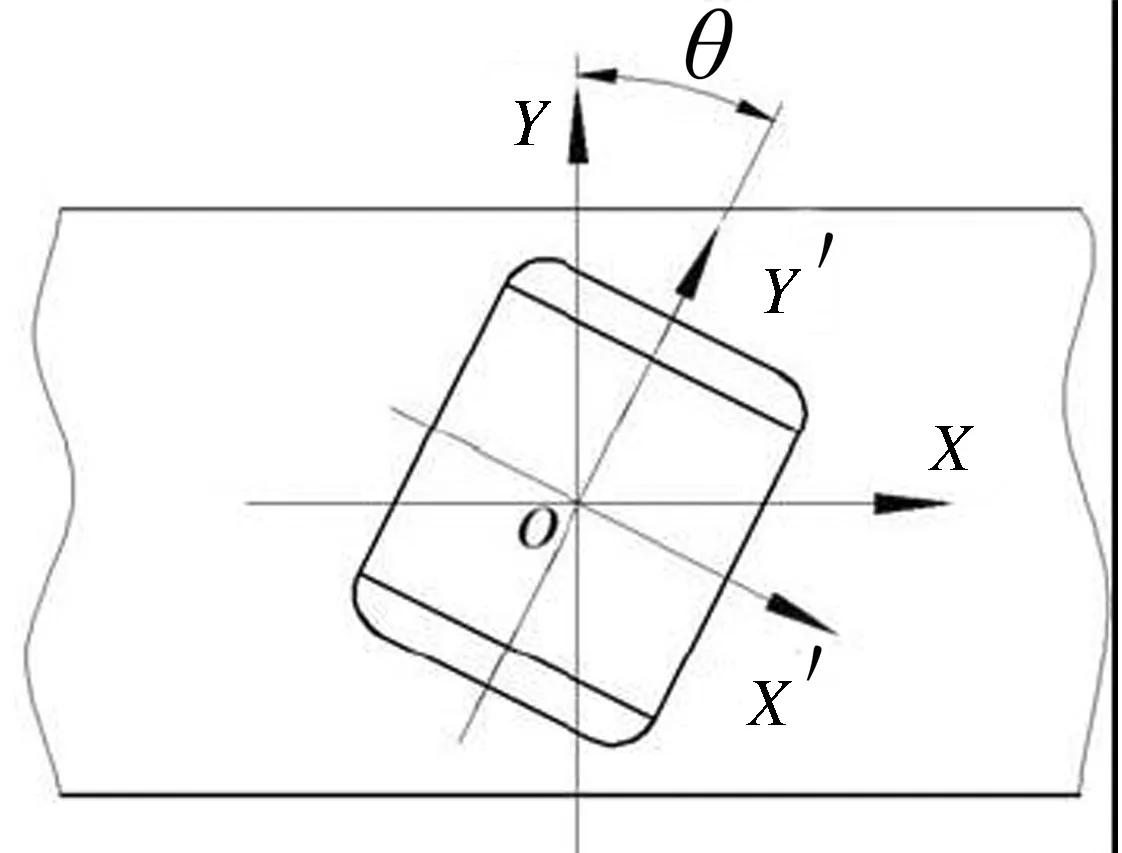
(b) 滚子歪斜图1 非歪斜滚子和歪斜滚子示意图

1.2 数值计算

1.2.1 膜厚方程

通过坐标转换法可得滚子歪斜后新的膜厚方程。滚子歪斜角θ随时间的改变而改变，设t时刻的歪斜角为θ(t)，转换坐标系后可得公式为

(1)

正常工况条件下，合理的非歪斜滚子和轴承外圈正常接触时的膜厚方程为[6]

(Y≤0时，取+；Y>0时，取-)

(2)

式中：若|Y|<0.5l时，fΔ取0；若|Y|≥0.5l时，fΔ取1；Ω为方程计算域；h00(t)为t时刻滚子刚体的中心膜厚，单位μm；E′为两刚体接触表面的弹性模量，单位Pa；RX1为滚子半径，单位mm；RY1为滚子修形半径，单位mm；P为t时刻油膜压力，单位GPa。

通过坐标转换法，用X,Y替代式(2)中的X′,Y′，得轴承滚子歪斜后的油膜厚度方程为

(Y≤0时，取+；Y>0时，取-)

(3)

式中：RX2为轴承外圈半径，单位mm；RY2为外圈边缘修形半径，单位mm。

1.2.2 载荷平衡方程

(4)

载荷平衡方程式中w(t)为t时刻承受的载荷，单位N，w(t)=w0·Cw(t)，w0为载荷参数，Cw(t)为承受载荷的动态系数。

采用Roelands黏度方程公式：

η=η0exp{A1[1+A2p]z0-1}

(5)

式中：η0为考虑温度和湿度的环境黏度；A1=lnη0+9.69；A2=5.15×10-9Pa-1；z0=α/(A1A2)，α为Barus黏度系数(Pa-1)。

2 滚子歪斜对润滑性能的影响

首先研究滚子是否歪斜对轴承的压力和膜厚的影响。图2、3分别给出滚子歪斜角θ=0和θ=2.4°时的膜厚和压力云图，除歪斜角外，其余几何参数均一致。

(a)膜厚云图

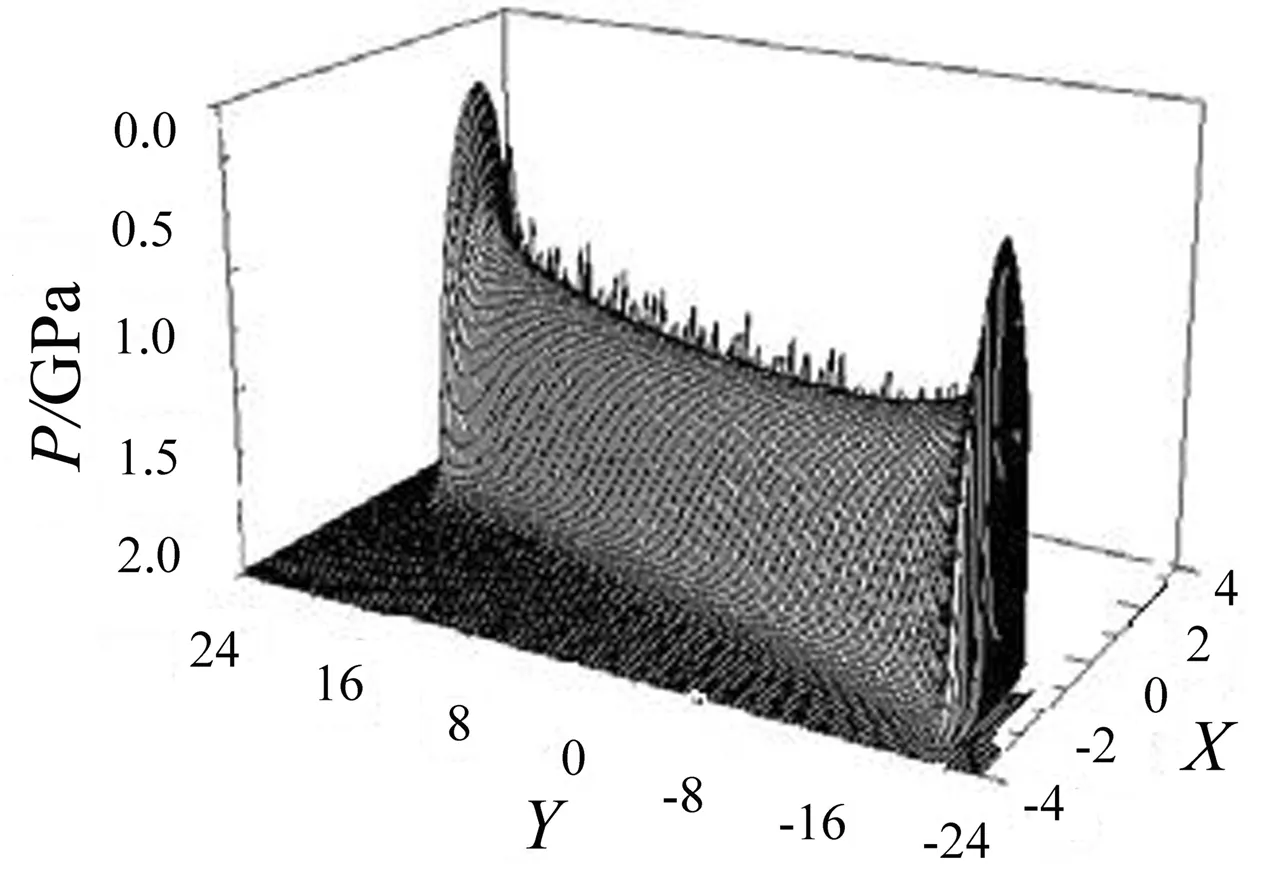
(b)压力云图图3 θ=2.4°时的压力和膜厚云图

从图2可知，滚子未发生歪斜时，膜厚和压力分布关于截面Y=0中心对称[7]；若忽略边缘效应不研究，滚子膜厚和压力大致沿其轴向均衡散开。

从图3可知，滚子歪斜一定角度后，接触区也相应歪斜一定角度，膜厚和压力总体上以滚子中心为对称点。与滚子歪斜前的膜厚和压力对比，歪斜后其端部膜厚减薄、压力扩张；中部膜厚和压力布局异常，越逼近中部，其膜厚越发厚重，而压力的数值越低。

为了进一步了解滚子歪斜角对其膜厚和压力的作用，表1给出了4种不同歪斜角下的膜厚和压力数值。由表1可见，当滚子歪斜角逐步增长，会导致中心膜厚变大、中心压力降低、压力峰值增大以及最小膜厚萎缩[8]。

表1 不同歪斜角下的中心膜厚(Hcen)、中心压力(Pcen)、最大压力(Pmax)和最小膜厚(Hmin)

综上所述，滚子歪斜会急剧降低轴承的润滑性能，除理想实验条件下，大多数实际情况中轴承均在非稳态条件下运行，因此对歪斜滚子副的非稳态润滑问题的研究，显得尤为重要。

3 歪斜滚子副在载荷冲击时的非稳态润滑问题

本文主要探讨歪斜滚子副在负荷变化的整个周期后又返回到最初状态的负荷冲击过程。

(6)

式中：Aw为载荷脉冲幅值；tp为载荷按正弦变化的时间(单位：s)。取Aw=2，tp=5×10-5s[9]。式中tp均分成200份。

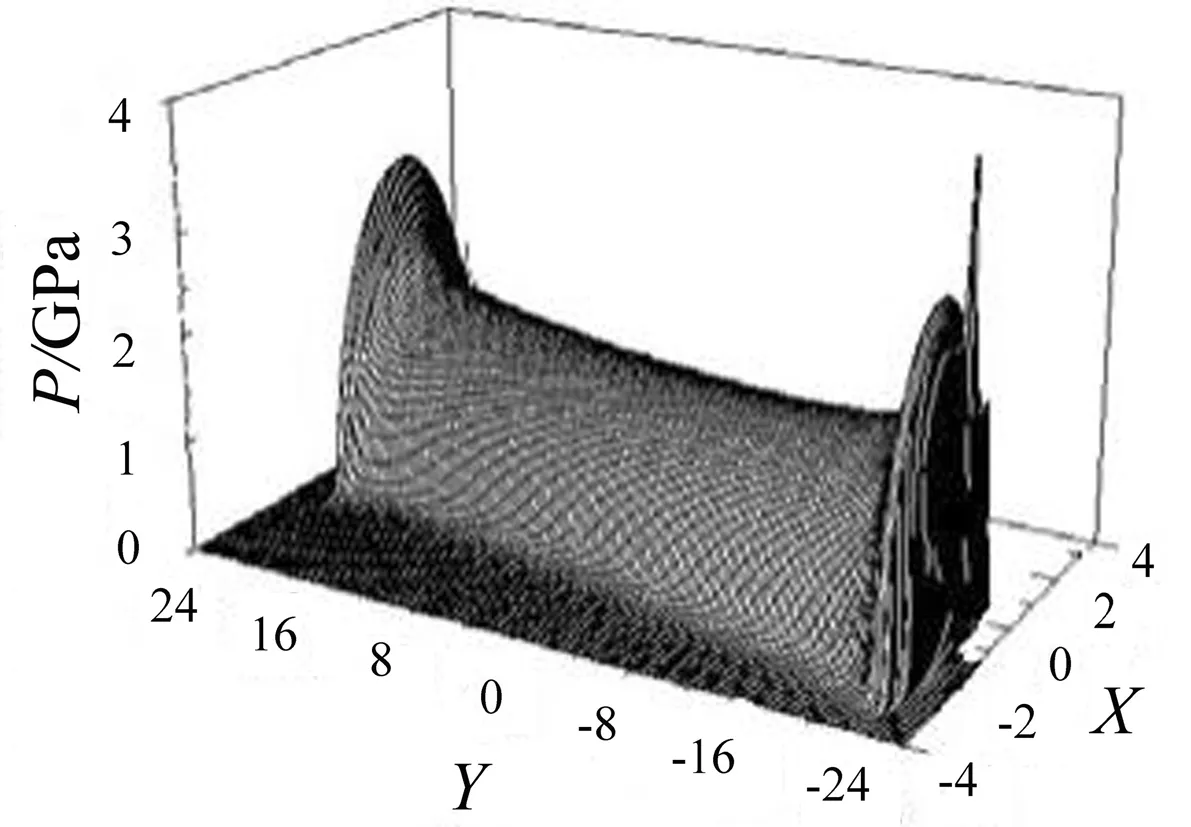
负荷突变时滚子歪斜角θ=2.4°时的压力云图，如图4所示。

从图4可知滚子歪斜后，其各个瞬时油膜接触区均产生较大程度的歪斜，且压力云图的布局

(a)t=0

(b)t=0.25tp

(c)t=0.5tp

(d)t=0.75tp

(e)t=tp

(f)t=2tp

不再以Y=0剖面对称。其端部仍为最大压力位置，与滚子无歪斜时一致。其中，突变负荷对油膜压力的变化极为明显，当t为(0～0.75tp)时突变负荷不断增大，油膜压力随突变负荷增大而增大；当t为(0.75tp～2tp)时突变载荷骤减，油膜压力随突变载荷减小而减小。当t=1tp时，突变负荷变化1个周期后回到最初值，油膜压力大体也回归初值。当t=2tp时，突变载荷完全停止变化，油膜压力完全回到初始状态，与t=0时刻的油膜状态几乎一致，呈现出周期性变化规律。

载荷突变时滚子歪斜角θ=2.4°时的膜厚云图见图5。由图可知膜厚云图的布局也不以Y=0剖面对称，膜厚最薄处为滚子端部。滚子承受突变负荷时，油膜厚度整体浮动幅度较小，但膜厚浮动表现出极其明显的周期性；由于冲击载荷使油膜表面产生形变，形成凹凸区域，致使油膜产生局部减薄和增厚现象。t=0.25tp时，凹陷区明显生成且处于入口附近，这时油膜云图呈现出阶梯状；t=0.5tp时，凹陷区明显转移至相交处中心，且此处膜厚呈下降趋势；t=0.75tp时，凹陷区由中部向X正方向移动(油膜颈缩处)；t=1tp时，凹陷区进一步向X正方向移动(逐步离开颈缩处)；t=2tp时，凹陷区全部脱离接触区，油膜完全回到最初状态，呈现出明显的周期性变化规律。

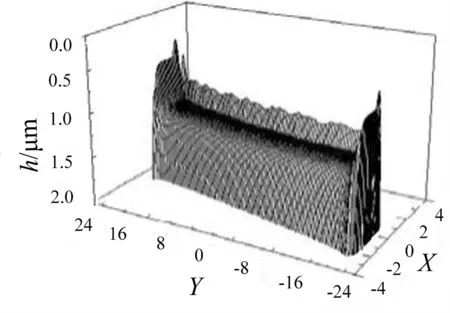
(a)t=0

(b)t=0.25tp

(c)t=0.5tp

(d)t=0.75tp

(e)t=tp

(f)t=2tp

(a)压力云图

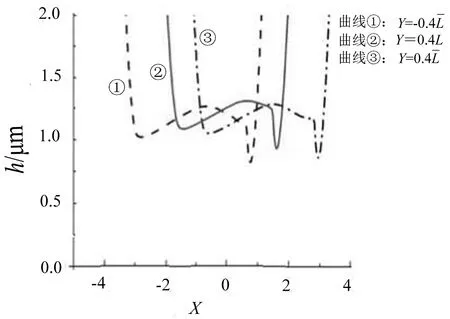
(b)膜厚云图图6 不同截面的压力和膜厚云图

为了分析滚子歪斜对动态弹流润滑问题的影响，图7对比了载荷冲击下θ=0和θ=2.4°时最大压力和最小膜厚随时间的变化。由图可见，与未发生歪斜时的最大压力和最小膜厚相比，滚子歪斜后的最大压力随时间变化的幅值显著增大，最小膜厚的波动幅度增大，大多数时刻的最小膜厚变得更小。因此，在载荷冲击过程中，较大的滚子歪斜角会使润滑状态更加恶劣。图中最小膜厚的变化曲线并不光滑，这是由于最小膜厚的位置随时间发生了变化甚至发生跳跃的缘故。两种歪斜角度下最小膜厚相对于载荷变化都有明显的滞后性，都大约在t=1.5tp时回到初值。