空间斜孔数控加工方法研究与实践
2022-07-12杨萍徐亮徐小飞
杨萍,徐亮,徐小飞
(安徽机电职业技术学院机械工程学院,安徽 芜湖 241002)
在数控机床加工中经常会遇到一些常规定位方法安装时与机床主轴或刀具既不平行也不垂直的空间任意斜孔的加工问题[1]。加工该类空间双偏转斜孔,必须事先根据零件定位特征准确地计算出相关定位角度,同时要保证相关角度在加工中能够通过工装精确地调整,并且在数控加工环境中进行有效的工艺实施。现通过实例对该类问题进行探究,本文采用球面法计算空间双偏转斜孔加工时的定位角度。运用课题组设计的空间角度调整组合夹具进行工件精确定位,创新坐标转换计算法得出空间双偏转斜孔数控加工对刀数据,最后利用加工中心(VMC850B)对零件实施加工。
1 空间偏转直线的角度计算
图1为某零件加工示意图,该零件有一斜孔轴线为空间任意直线,加工时要求将斜孔轴线定位成铅垂方向。

图1 空间斜孔零件示意图
该空间斜孔理论上可通过2次旋转完成定位[2]。设已知α,γ,有tanα=x/z,tanγ=y/z,则:
tanβ=y/x=tanγ/tanα
(1)
进而求出β,此角为斜孔轴线第1次绕Z坐标轴逆时针方向转过的角度。
由空间直线角度方程可求得孔直线与平面XOY的倾角δ:
(2)
通过式(2)即可求得δ,90°-δ为斜孔轴线第2次绕Y坐标轴顺时针方向转过的角度,经过上述2次角度旋转可使斜孔轴线定位到铅垂位置进行钻孔加工。
以上为理论上的2次绕坐标轴角度旋转将空间斜线变成铅垂的理想状态,实践中考虑零件的定位方法和工装结构,无法进行有效操作。
2 基于球面法的空间斜孔定位计算
对空间双偏转孔系零件的数控加工定位,可以运用角度组合夹具定位进行有效操作,先将角度组合夹具组装出定位角θ,再将工件在夹具定位面上扭转,定向角为φ,即可以进行加工。
某斜面定位具有空间双偏转角度孔加工的工件简图,见图2,由结构简图可知各部分尺寸和零件图上投影角分别为14°和18°,工件以底斜面为主定位,以一侧面进行定向,钻直径为5 mm的通孔。

图2 孔加工零件简图
2.1 V-球面图法
选主视图作V-球面图,建立V-球面图,见图3。
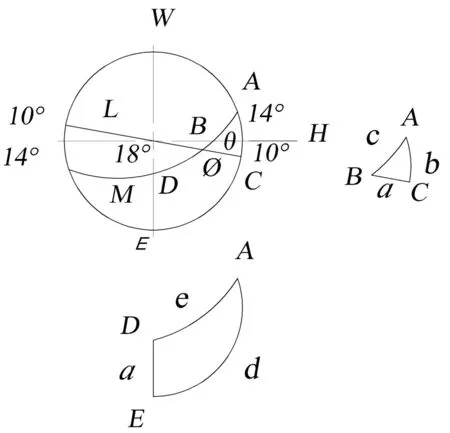
图3 V-球面图
首先将工件定位面移入,L为定位面,M为与通孔轴线垂直的钻孔对刀平面,即M为加工面,θ即为定位角,它是定位面与对刀加工面之间的夹角,φ为定位面上定向线与基准线之间的夹角,即定向角。
在球面直角三角形AED中,E为90°,d为104°,a为72°。
由球面直角三角形计算公式[3]得
ctgA·tga=sind
(3)
在球面直角三角形ACB中,C为90°,A为72.5°,b为24°,由球面直角三角形计算公式得
cosB=sinA·cosb
(4)
B就是所求定位角θ,其值为29°23′24″。
在球面直角三角形ACB中,b为24°,B为29°23′24″,由三角函数关系式可得:
sina=tgb·ctgB
(5)
a=52°13′16″
(6)
a就是所求定向角φ,其值为52°13′16″。
2.2 H-球面图法
若选俯视图作H-球面图,建立H-球面图,如图4所示。定位面、加工面如图4所示,θ角即为定位角,φ为定向角。

图4 H-球面图
在球面直角三角形ABC中,
已知:C=90°,b=90°-14°=76°,a=90°-18°=72°
求:A。
解:由球面直角三角形公式,得
sinb=tga·ctgA
(7)
A=72.502°=72°30′5″
(8)
在球面直角三角形A′B′C′中,
已知A′=72.502°,b′=90°-10°+76°=156°
求:B′,a′。
解:由球面直角三角形公式得
cosB′=sinA′·cosb′
(9)
cosB′=sin 72.502°·cos 156°=0.953 72×(-0.913 55)=-0.871 27
(10)
B′=150°36′24″。
定位角θ:
θ=180°-B′=180°-150°36′24″=29°23′24″
(11)
sinb=tga′·ctgA′
(12)
a′=52.221°=52°13′16″
(13)
定向角φ=a′=52°13′16″。
2.3 W-球面图法
若选左视图作W-球面图,建立W-球面图,如图5所示,定位面、加工面如图5所示,θ角即为定位角,φ为定向角。

图5 W-球面图
在直角三角形A′B′C′中,
已知:C′=90°,b′=90°-14°=76°,a′=18°+90°=108°
求:A′。
解:由球面直角三角形公式得
sinb′=tga′·ctgA′
(14)
A′=72.502°=72°30′7″
(15)
在直角三角形ABC中,
已知:C=90°,a=10°+14°=24°,B=180°-72°30′7″。
求:A,b。
解:由球面直角三角形公式得
cosA=sinB·cosa
(16)
A=29.392°=29°23′32″
(17)
定位角θ=29°23′24″ 。
sina=tgb·ctgB
(18)
b=50.221°=52°13′16″
(19)
定向角φ=b=52°13′16″。
以上分别运用V-球面图法、H-球面图法和W-球面图法计算出在数控加工中心上加工直径为5 mm空间斜孔的定位角和定向角分别为29°23′24″和52°13′16″。
3 零件空间斜孔数控加工组装定位
3.1 高精度角度组合夹具的设计
结合空间双偏转孔系加工的定位特征,本课题组专门设计出一套高精度双偏转角度调节组合夹具,如图6所示。构成组合夹具主体的上下支撑板设计有矩阵式间隔排列的螺栓孔和销孔。
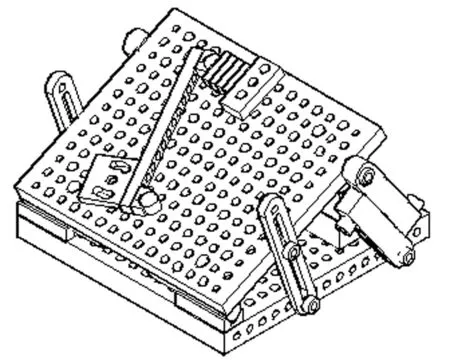
图6 双偏转角度调节组合夹具
用V形块加切边轴结构代替了原来角度组合夹具常用的铰链结构,V形块限位基准构成了夹具角度调节的回转中心。该套组合夹具中切边轴及V形块在下支撑板上的组装图(本文零件加工支撑板上定位孔为矩阵式排列设计),如图7和图8所示。下支撑板组装有相应位置的V形块,切边轴与V形块均通过销与螺钉和支撑板定位连接,3个切边轴分别与3个V形块接触定位并呈品字状分布,使用该结构定位时,安装方便,对中性好,可提高定位精度。

图7 切边轴组装

图8 V形块在下支撑板上组装
组合夹具的上下支撑板与量块组构成直角三角形(见图9),通过双V形块加双切边轴的设计,利用正弦原理实现组合夹具定位角的调节[4]。双切边轴间距L为定值,调整量块组高度H可达到调整角度的目的,从而构成双V形块加双切边轴的多角度调节柔性组合夹具。
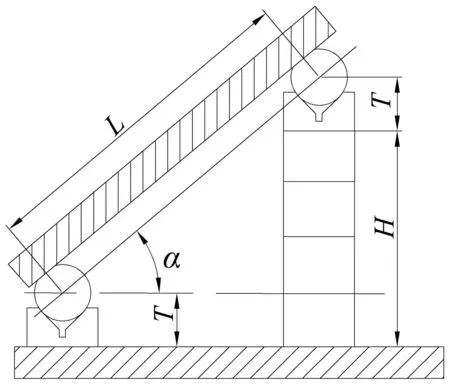
图9 组合夹具定位角调节原理
该组合夹具上下支撑板的定位角度θ可以通过H精确调节,调整角度计算公式:
(20)

当组合夹具上下支撑板定位角调整好后,再利用角度工作台支撑板上的一套角度定位组件完成工件另一个定向角度的精确偏转,定位组件结构设计如图10所示,该套定位组件在角度组合夹具上支撑板上完成定向角的调节。

图10 定向角调整示意图
角度工作台上支撑板具有矩阵式的间隔排列的螺栓孔和销孔,图10的定位组件中左下角为插入上支撑板销孔的阶梯销,其轴线为角度调节的回转中心,双V型块间距为定值L,L与量块组构成直角三角形的斜边与直角边,该套定位组件可以在角度工作台支撑板上精确旋转,得到定向角φ。
该定向角调整公式如下:
sinφ=(H+a+b)/L
(21)
图10定位组件中带腰圆沉孔的方块件可精确获得定向角位置,该方块件是工件定向偏转的定位元件,定位组件的其他元件可拆卸,双偏转角度调节组合夹具组装完毕。
3.2 零件数控加工安装
某零件数控加工时在组合夹具上的空间位置安装示意图如图11所示。使用该装置可以完成直径为5 mm孔加工的精确定位和定向,保证零件的加工精度,满足此类零件的加工要求。
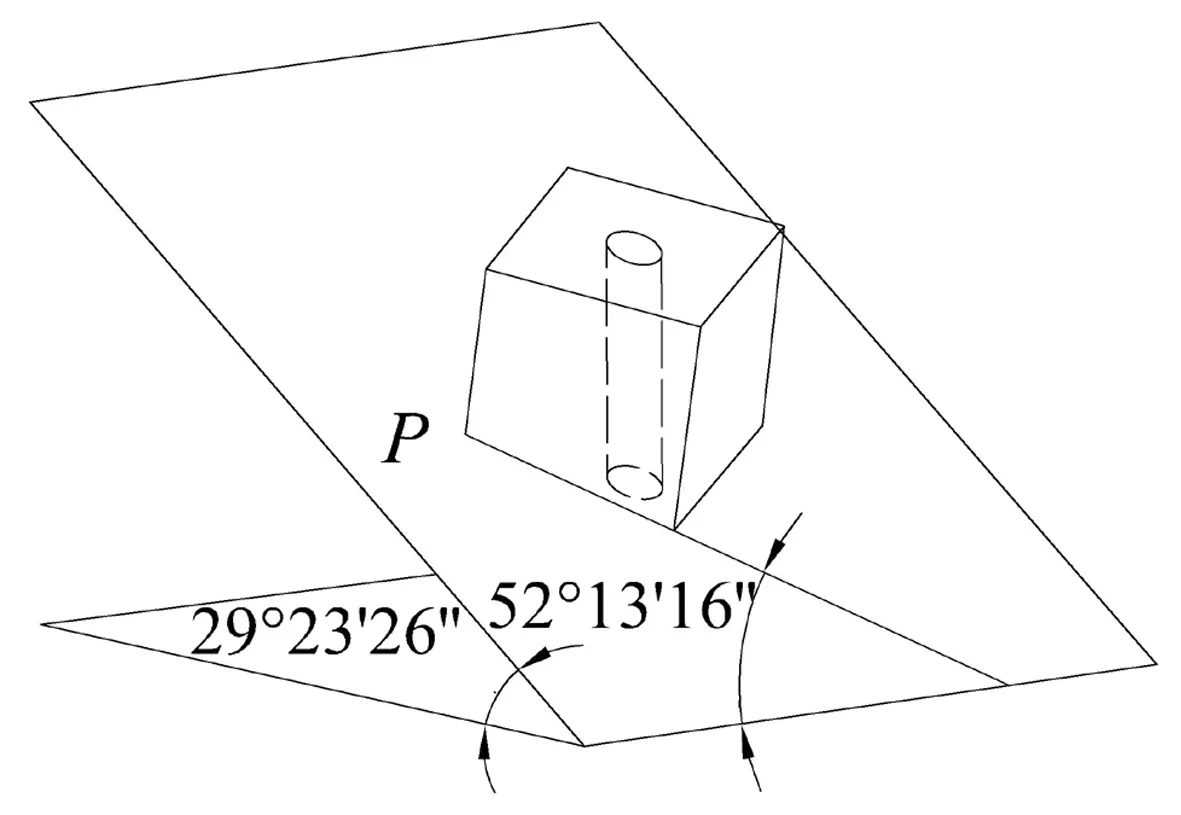
图11 安装定位示意图
角度组合夹具安装工件后的仿真模拟示意图,如图12所示。在钻直径为5 mm的斜孔时,可以先将该组合夹具按定位角29°23′24″组装,然后通过图10所示的定位组件在角度工作台支撑板上将工件按定向角52°13′16″旋转,确保该斜孔垂直于机床工作台,从而保证加工位置精度。

图12 组合夹具实际安装图
3.3 角度组合夹具坐标系设定
该零件加工定位时以角度组合夹具下底板为基准建立的XYZ笛卡尔坐标系如图13所示。该坐标系以数控机床为基准建立,与加工中心的机床坐标系同向。
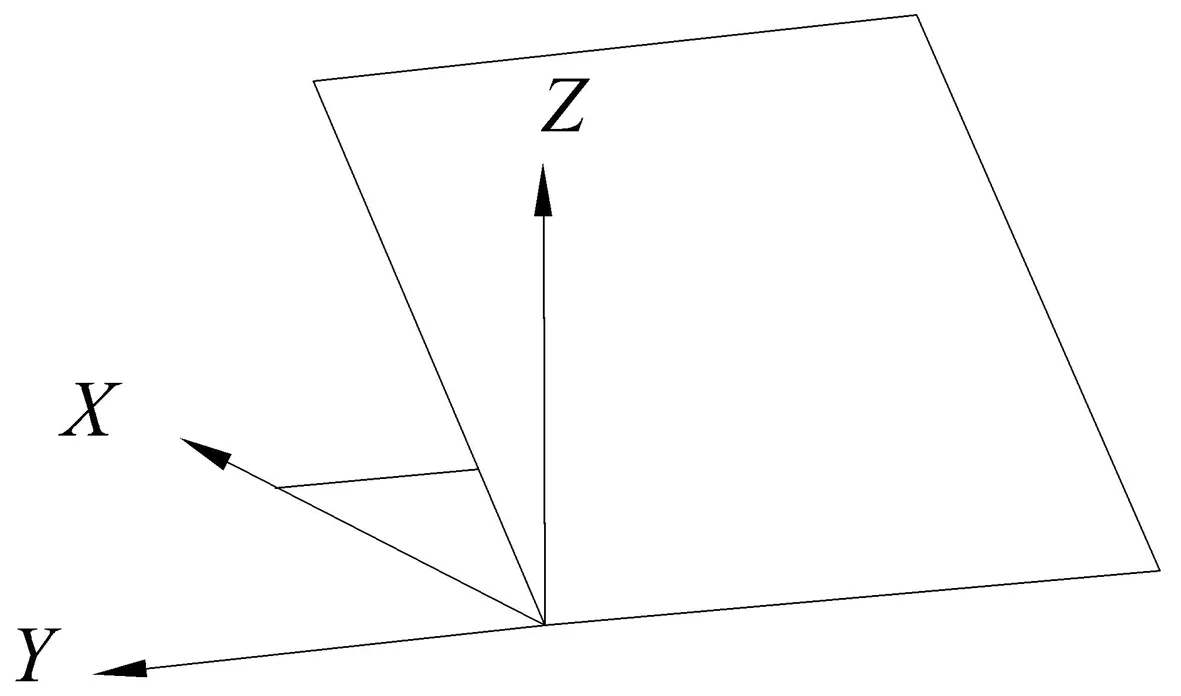
图13 组合夹具XYZ坐标系设定
3.4 零件在组合夹具上的定位模拟
沿X方向所看到的零件定位后的投影视图如图14所示。由图可见,按照计算的定位角和定向角安装放置后加工孔垂直于工作台,满足加工条件。

图14 沿X方向投影视图
沿Y方向所看到的零件定位的投影视图如图15所示。由图可见,按照计算的定位角和定向角安装放置后加工孔垂直于工作台,满足加工条件。
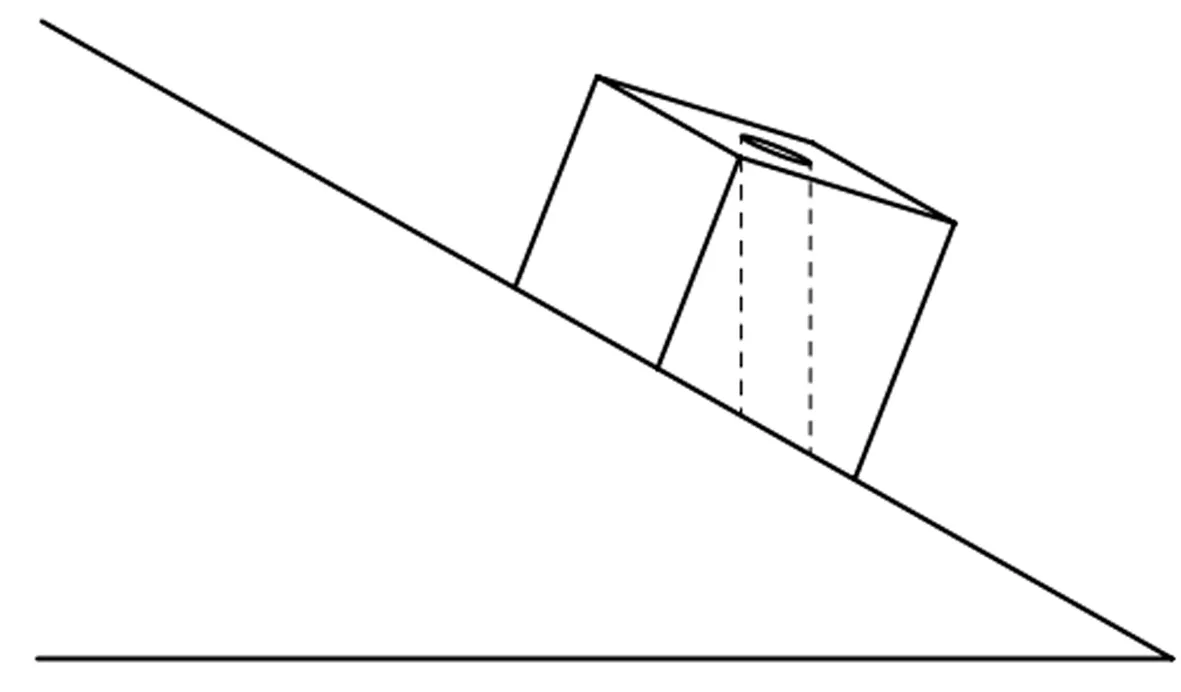
图15 沿Y方向投影视图
4 空间斜孔数控加工对刀计算
4.1 坐标系设定
如图16所示,设定零件在数控加工中心机床上加工安装时,以零件上特征点P为对刀计算基准点,P点的坐标位置可以由调整后的组合夹具结构尺寸得到,加工对刀用M点[5](工件待加工孔的上孔位中心)的位置尺寸可以由零件结构尺寸和相关坐标转换计算求得。
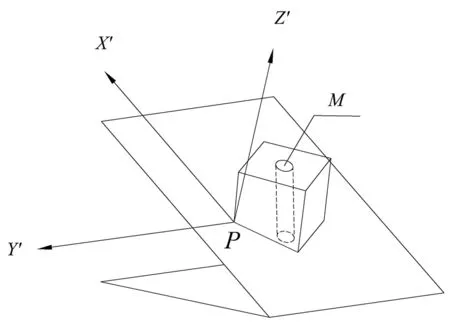
图16 X′Y′Z′坐标系示意图
以P点为坐标原点分别建立以机床工作台为基准的XYZ坐标系[6](图13)、以角度组合夹具上支撑板(定位基准面)为基准的X′Y′Z′坐标系(图16)和以零件本体为特征的X′Y′Z′坐标系,对加工直径为5 mm孔时的对刀点M进行坐标尺寸转换计算,即用直角坐标转换公式计算M点到P点的X、Y、Z方向的坐标值,再结合P点的坐标,得到M点对刀尺寸[7]。
4.2X″OY″-X′OY′坐标转换
建立X″OY″-X′OY′直角坐标系,见图17。
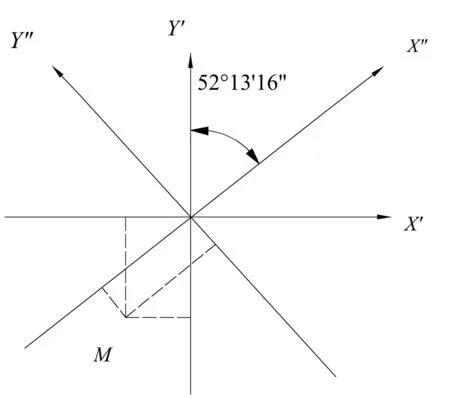
图17 X″OY″-X′OY′坐标转换
由图17可知:
X′=X″·cosφ-Y″·sinφ=X″·cos 37°46′44″-
Y″·sin 37°46′44″
(22)
Y′=X″·sinφ-Y″·cosφ=X″·sin 37°46′44″-Y″·cos 37°46′44″
(23)
4.3X′OZ′-XOZ坐标转换
建立X′OZ′-XOZ直角坐标系,见图18。

图18 X′OZ′-XOZ坐标转换
由图18可知:
X=X′·cosθ-Z′·sinθ=X′·cos 29°23′24″-Z′·sin 29°23′24″
(24)
Z=X′·sinθ-Z′·cosθ=X′·sin 29°23′24″-Z′·cos 29°23′24″
(25)
以上方法可求得加工对刀M点在XYZ机床坐标系的坐标位置。
5 加工验证
在加工中心设备(VMC850B)上对零件双偏转斜孔进行加工,如图19所示。

图19 运用加工中心(VMC850B)实践加工
用课题组设计的高精度双偏转角度调节组合夹具进行定位,按计算得出的定位角θ和定向角φ,将工件连同组合夹具在机床工作台上调整好,结合机床和组合夹具结构,采用坐标转换法计算结果进行数控加工对刀。经过加工验证,以上研究有效地解决了空间斜孔加工定位难这一问题,改善了该零件的加工工艺,提高了加工精度。
6 结论
通过以上典型案例,重点研究了球面法求解某零件空间角度孔加工时的定位角和定向角的方法,分别采用V-球面法、H-球面法和W-球面法计算了该斜孔加工时的定位角和定向角,结果表明求出的空间角度值一致,验证了计算方法的正确性和可行性。
从上述实例可以看出,用球面三角形求解空间角度是一种很简单实用的方法。运用球面图法可以计算出此类零件的定位角和定向角,同时完全适用于角度组合夹具的安装调整,便于此类零件的空间斜孔钻削加工,解决了此类零件安装定位困难等问题。
课题组设计了可精确柔性调节空间工位角度的组合夹具工装,用于零件双偏转角度孔系数控加工时的精确定位。
借助对刀基准转换点,以零件上特征点为原点,通过构建基于零件及其加工环境特征的三重直角坐标系统(即零件坐标系、夹具定位坐标系和数控机床坐标系),利用二维坐标转换方法,求出数控加工孔系的对刀尺寸,进而顺利地进行数控加工。
运用以上研究,在数控加工中心(VMC850B)加工出了实物,验证了新工艺方案的精确性、便捷性、可靠性和可操作性。
