经济发展、中等职业教育与人力资本研究——基于面板数据的PVAR模型

玉苏普伊力·喀迪尔 庄馨予

（新疆财经大学 财政税务学院，新疆 乌鲁木齐 830012）

国内学者从财政资金的充足性和公平性阐述了中等职业教育财政投入的必要性，同时从宏观和微观层面对中等职业教育与经济增长的关系展开研究，但鲜有学者从经济发展、财政投入、人力资本培育三者的联动关系对中等职业教育进一步研究，本文利用2007—2018年全国31个省（区、市）的面板数据，采用PVAR模型研究经济发展、财政投入与中等职业教育人力资本培育三者间的动态关系。

一、变量选择及模型构建

1.变量选择

经济发展指标为pgdp，以人均地区生产总值（元）测度，衡量各地经济发展水平。中等职业教育财政投入指标为medu，以中等职业教育国家财政性教育经费（亿元）测度，代表国家财政对各地区中职教育的财政资金支持力度。中等职业教育人力资本培育指标为mlabor，本文假定中等职业教育毕业生均能转化为劳动力市场中的成熟劳动力，故以中等职业教育毕业生数量（人）代表中职院校为经济发展培育的人力资本。

为消除价格因素影响，本文以1978年为基期采取平减指数法对与物价相关的经济数据进行平价处理，并采用取对数的方法消除可能存在的序列异方差，生成 lnpgdp、lnmedu、lnmlabord。

2.数据来源

本文人均GDP数据来源于2008—2019年《中国统计年鉴》，中等职业教育毕业生数量来源于2007—2018年《中国教育统计年鉴》，中等职业教育国家财政性教育经费来源于2008—2019年《中国教育经费统计年鉴》。

3.PVAR模型构建

PVAR模型继承了传统VAR模型的优点，即将各变量视作内生变量，无须提前设定变量间的因果关系，同时将样本数据的要求扩展至“时序短、截面大”的面板数据，能够综合考量样本的固定效应和时间效应。

面板数据在经过平稳性检验和滞后阶数选择后，一般采用广义矩估计（GMM）的方法来估计PVAR模型，初步报告各变量的滞后项对变量的影响，并通过脉冲响应分析特定变量的随机扰动对其他变量的冲击，通过方差分解评价特定变量冲击对各变量变动的影响程度，进而全面分析各变量间的动态关系。

本文构建PVAR模型如下：

其中，i代表不同省（区、市），t代表年份，Yit为包含代表人均GDP（元）、中等职业教育国家财政性教育经费（亿元）、中等职业教育毕业生数量（人）的三维列向量，δ0和εit分别代表截距项向量和扰动项向量，k代表滞后阶数，δj代表滞后j阶的参数矩阵，αi和βi分别代表个体效应和时间效应向量。

二、实证验证

1.描述性统计

考虑到我国地区间经济发展不平衡，本文对全国31个省（区、市）进行了如下区域划分（见表1）。

表1 区域划分标准

全国及东、中、西部三大区域各项指标描述性统计结果如表2所示，东部地区人均GDP高于全国平均水平，其次是中部地区，西部地区人均GDP最低，中等职业教育国家财政性教育经费投入的区域特征与各区域经济发展特征基本一致，而中等职业教育毕业生数量则呈现“中部地区＞东部地区＞全国平均水平＞西部地区”的特点。

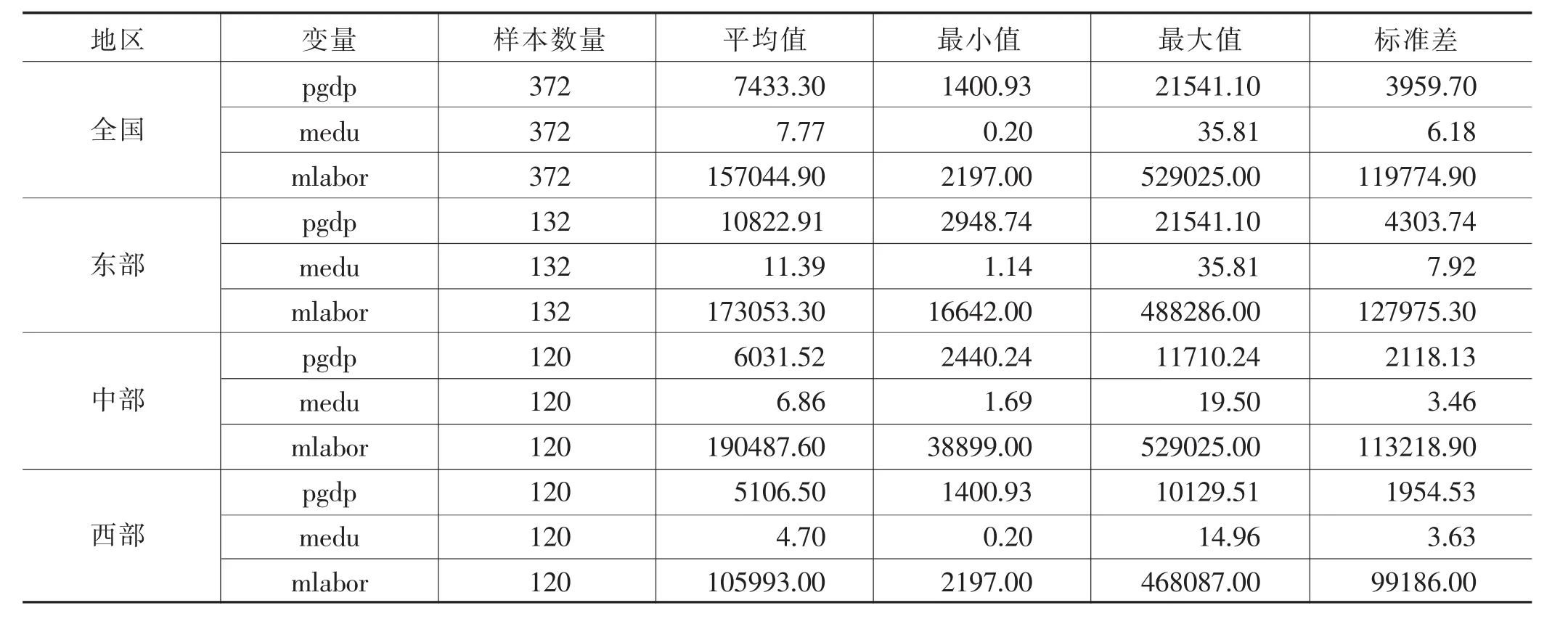
表2 描述性统计

2.平稳性检验

为避免变量不平稳造成伪回归，本文选用同质单位根的LLC检验和异质单位根的IPS检验对lnpgdp、lnmedu、lnmlabord 及其一阶差分序列 dlnpgdp、dlnmedu、dlnmlabord进行稳健性检验。表3展示了软件STATA15.1对各变量分区域单位根检验的结果，可见全国及东、中、西部三大区域 lnpgdp、lnmedu、lnmlabord大多无法拒绝“变量非平稳”的原假设，而其一阶差分序列dlnpgdp、dlnmedu、dlnmlabord基本均在 99%的显著性水平下拒绝了“变量非平稳”的原假设，可将其视为平稳序列，不存在单位根，可以进行PVAR模型估计。

表3 平稳性检验

（续表）

3.滞后阶数选择

通过平稳性检验后，根据样本数据特征确定各区域PVAR模型适用的滞后阶数。本文选用AIC、BIC、HQIC三大信息准则确定全国与东、中、西部各模型的最优滞后阶数选择，通常三大信息准则以相应统计量最小值所在的滞后期作为建议选择的模型滞后阶数。由表4可知，全国和西部地区PVAR模型的最优滞后阶数为3，东部和中部地区PVAR模型的最优滞后阶数为1。

表4 滞后阶数选择

4.PVAR模型估计

为消除PVAR模型中的时间效应和个体固定效应，采用截面均值差分法和前项均值差分法（Helmert）生成 h_dlnpgdp、h_dlnmedu、h_dlnmlabord，再运用系统GMM模型对其进行PVAR估计，以消除模型中变量的内生性问题。估计结果详见表5，表中L1、L2、L3分别代表相应变量的1阶滞后值、2阶滞后值以及3阶滞后值。

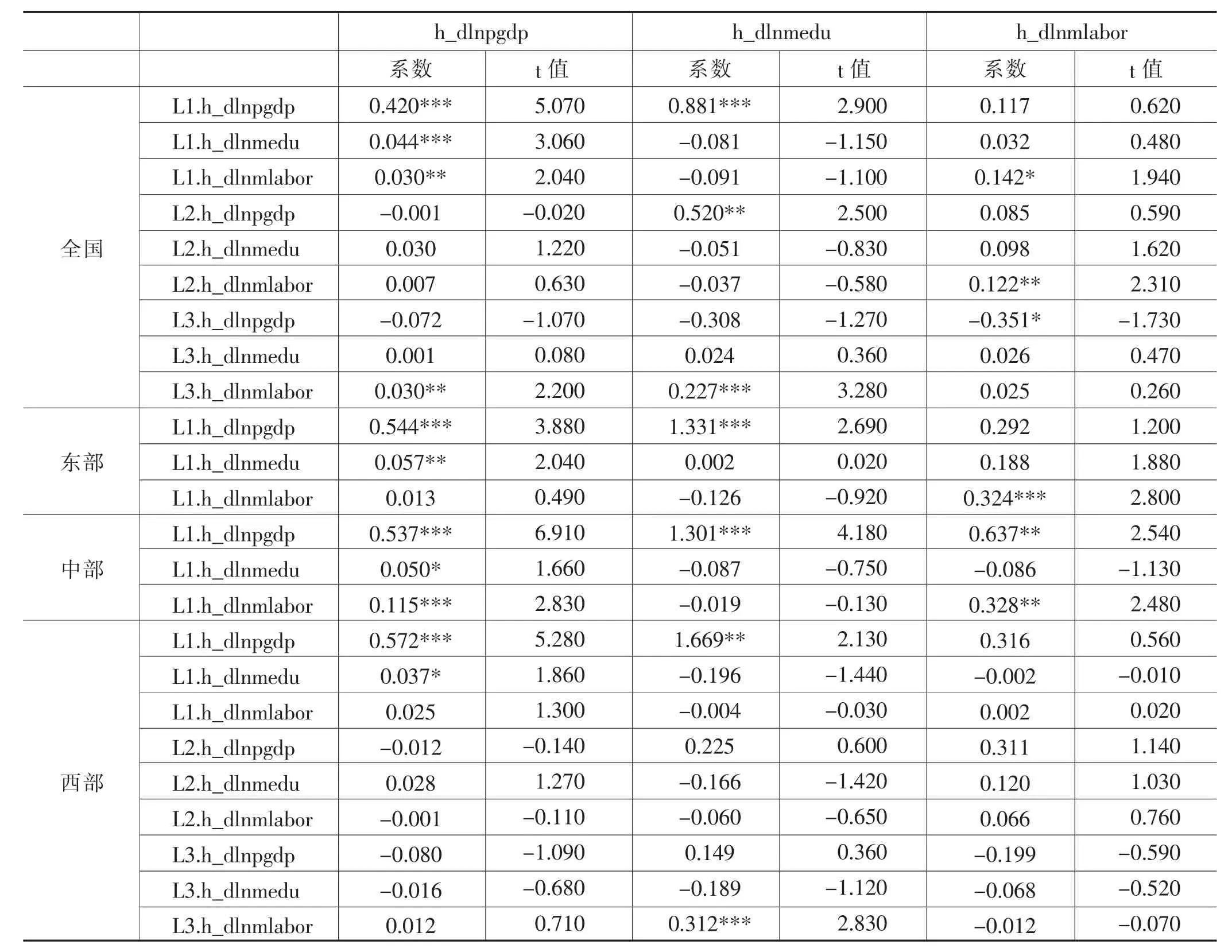
表5 PVAR模型估计结果

（1）将经济发展水平作为被解释变量

从全国看，经济发展与其一阶滞后值显著相关，其影响系数高达0.420，同时中等职业教育财政投入与人力资本培育在滞后1期的情况下能够对经济发展产生显著的正效应。值得注意的是，中等职业教育所培育的人力资本在滞后1期和滞后3期的情况下均能够显著促进经济发展，可见其对经济发展的影响不容小觑。

分区域看，三大区域的经济发展水平与其自身一阶滞后值及中等职业教育财政投入一阶滞后值均显著正相关，但东部地区中等职业教育财政投入对经济发展的推动作用更强，中部地区次之，西部地区相对较弱。值得注意的是，东部地区和西部地区中等职业教育的人力资本作用并不显著，与此同时，中部地区中等职业教育的人力资本属性较强，对经济发展的正向作用十分显著，可见中部地区中等职业教育人力资本培育在较大程度上促进了区域经济发展。

（2）将中等职业教育财政投入水平作为被解释变量

从全国看，经济发展能够为中等职业教育财政投入提供较多的资金支持，经济发展水平的一阶滞后值及三阶滞后值对中等职业教育财政投入的解释系数均超过0.5，且十分显著，可见中等职业教育财政投入十分依赖经济发展水平。从回归结果看，中等职业教育人力资本培育在滞后3期的情况下呈现出对中等职业教育财政投入的显著正向作用，可见其对财政投入的拉动作用存在一定滞后性。

分区域看，东部地区和中部地区中等职业教育财政投入仅与其经济发展水平的一阶滞后值显著正相关，西部地区中等职业教育财政投入不仅与经济发展水平有关，还受中等职业教育人力资本培育水平三阶滞后值的影响，可见中等职业教育的人力资本作用不仅在时间上存在滞后性，还存在一定区域差异。

鉴于大多中等职业教育采用3年制的培育模式，因此这种现象可以看作是中等职业教育毕业生对政府财政支持的一种现实需求。

（3）将中等职业教育人力资本培育水平作为被解释变量

从全国看，中等职业教育人力资本培育水平的一阶滞后值和二阶滞后值对其影响系数并不高，分别为0.142和0.122。值得注意的是，在90%的置信水平下，经济发展水平的三阶滞后值对中等职业教育人力资本培育水平的解释系数显著为负，为-0.351，可见经济发展水平的提高在一定程度上会导致市场对中等职业教育毕业生数量的需求减少，中等职业教育的人力资本培育水平会受到一定限制。

分区域看，东部地区中等职业教育人力资本培育水平主要受其自身一阶滞后值影响，且影响显著为正。中部地区中等职业教育人力资本培育水平受其自身一阶滞后值和经济发展水平一阶滞后值的共同影响，二者的影响均显著为正，且经济增长水平的影响系数较大。西部地区各变量滞后值对其中等职业教育人力资本培育的影响均不显著，可见各地区经济发展水平和中等职业教育财政投入不同，对中等职业教育人力资本培育的影响也存在显著差异。

5.脉冲响应函数

本文将冲击时期设定为10年，从脉冲响应函数的收敛趋势可以看出本文所构建的PVAR模型是稳健的。

（1）全国地区脉冲响应函数

从全国看，经济发展受到一个单位正标准差冲击后，会对其自身、中等职业教育财政投入及中等职业教育人力资本培育产生正向冲击，这种冲击影响对自身的冲击作用力最大，对中等职业教育财政投入较小，对中等职业教育人力资本培育的冲击作用力最小，在第3期后会逐渐减弱并趋于0。这说明经济发展水平的提升能够在一定程度上促进中等职业教育财政投入的增加，同时能够在一定程度上增加对中等职业教育人力资本培育成果的消化（见图1）。

图1 脉冲响应图（全国）

当中等职业教育财政投入受到一个单位正标准差冲击后，会对经济发展水平产生正向冲击，这种冲击反应在第1期末达到峰值，随后下降至第3期后渐近平稳。其自身和中等职业教育人力资本培育对其冲击的反应在正向与负向间波动，同样在第3期后渐进收敛。这说明中等职业教育财政投入对拉动经济发展具有积极作用，同时对中等职业教育人力资本培育具有重要意义。

当中等职业教育人力资本培育受到一个单位正标准差冲击后，其自身的反应程度最大，中等职业教育财政投入的反应程度较小，经济发展的反应程度最小。这说明中等职业教育财政投入对人力资本培育存在一定依赖性，而经济发展对等职业教育人力资本培育的依赖性相对较小。

（2）东部地区脉冲响应函数

从东部地区看，经济发展、中等职业教育财政投入和中等职业教育人力资本培育均在当期对自身产生较大正向冲击，随后冲击作用迅速下降，在第1期后逐渐趋于0。经济发展受到一个单位正标准差冲击后，中等职业教育财政投入与人力资本培育的正向反应会在第1期末达到峰值，随后渐进趋于平稳。与全国脉冲响应函数结果相比，东部地区各变量对经济发展冲击的反应更强烈，但缺乏持续性（见图2）。

图2 脉冲响应图（东部地区）

当中等职业教育财政投入受到一个单位正标准差冲击后，会在第1期对经济发展水平产生最大的正向冲击，对中等职业教育人力资本培育产生最大的负向冲击，尽管在第1期后这种冲击作用力会逐渐变小，但依旧可以看出稳定中等职业教育财政投入的现实必要性。与全国平均水平相比，东部地区经济发展水平和中等职业教育财政投入对中等职业教育人力资本培育的反应更敏感、更强烈。

（3）中部地区脉冲响应函数

从中部地区看，经济发展受到一个单位正标准差冲击后，会对其自身、中等职业教育财政投入及中等职业教育人力资本培育产生正向冲击，其脉冲响应函数具体变化趋势与东部地区较为类似。与全国平均水平相比，中部地区经济发展对其自身的反应较大，同时，中等职业教育人力资本培育对经济发展反应相对较小（见图3）。

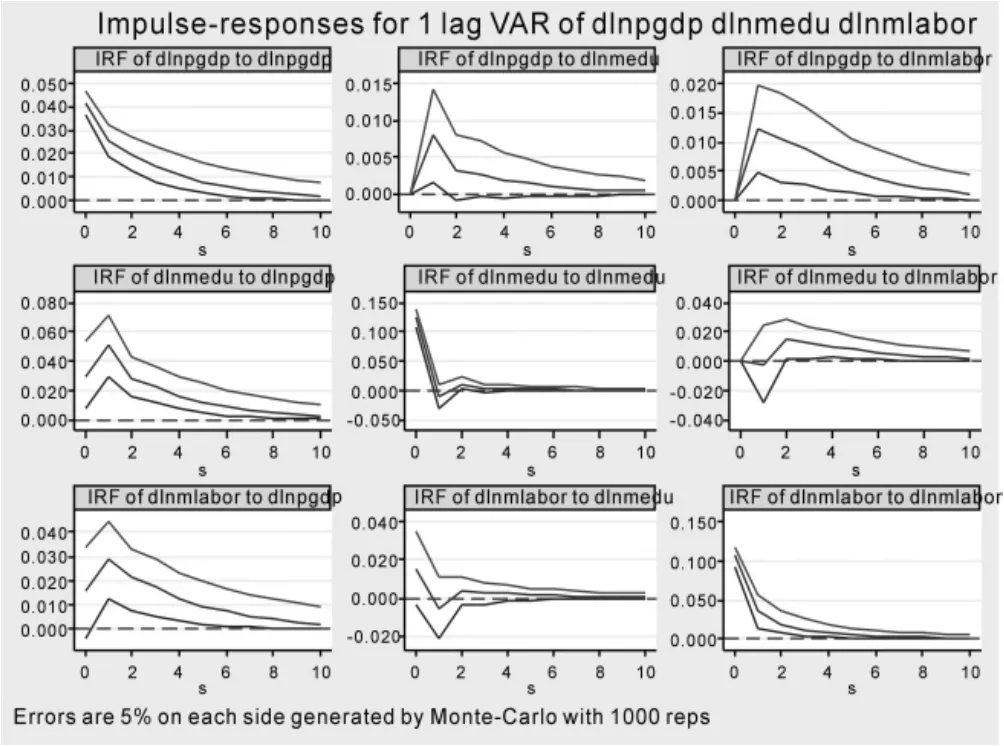
图3 脉冲响应图（中部地区）

当中等职业教育财政投入受到一个单位正标准差冲击后，会对经济发展水平产生正向冲击，这种冲击反应在第1期末达到峰值后大幅下滑，第2期后渐近趋于0，其自身和中等职业教育人力资本培育对其冲击的反应则在正向与负向间波动，且于第2期后渐近平稳。与全国平均水平相比，中部地区经济发展对中等职业教育财政投入的反应较大，同时，中等职业教育人力资本培育对中等职业教育财政投入反应相对较小。中部地区经济发展与中等职业教育财政投入对中等职业教育人力资本培育的反应程度均大于全国平均水平。

（4）西部地区脉冲响应函数

从西部地区看，经济发展受到一个单位正标准差冲击后，会对其自身产生正向冲击，对中等职业教育财政投入及人力资本培育产生负向冲击。当中等职业教育财政投入受到一个单位正标准差冲击后，会对经济发展水平产生正向冲击，对自身和人力资本培育产生负向冲击，当人力资本培育受到一个单位正标准差冲击后，会对其自身和经济发展水平产生正向冲击，对中等职业教育财政投入产生负向冲击（见图4）。

图4 脉冲响应图（西部地区）

6.方差分解

为进一步评估模型扰动项对内生变量冲击的影响程度及各变量变化过程中不同结构冲击的贡献力度，进一步对PVAR模型进行方差分解（见表6），取第5期、第10期来分析中等职业教育财政投入、人力资本培育与经济发展三者相互影响的贡献程度。

表6 方差分解

就全国而言，经济发展的方差贡献率主要受自身影响，在第10期时仍为89.1%，其次为中等职业教育财政投入、人力资本培育。东、中、西部地区的经济发展的方差分解结果与全国相似，在滞后10期时，东部地区经济发展方差贡献率受自身影响为96.5%，中部地区为85.9%，西部地区为90.5%。

从其他变量对中等职业教育财政投入的贡献度来看，在滞后10期后基本稳定，而且全国经济发展对中等教育投入的贡献率比人力资本培育的贡献率略高，全国经济发展对中等教育投入的贡献率约在10%左右，人力资本培育对中等职业教育财政投入的贡献率约为5%。东、西部地区对中等职业教育财政投入的贡献率有差异，东、中部地区大约为20%左右，西部地区为10%左右，经济发展是影响中等教育投入的重要影响因素。

从全国看，人力资本培育主要受自身影响，其次是中等教育投入，在滞后10期时，人力资本对自身的方差贡献率是95.5%，经济发展、中等职业教育人力资本培育的贡献率分别为0.6%、3.9%。东部地区的方差分解结果与全国类似，中部地区的人力资本培育方差贡献率主要来自自身与经济发展水平，分别为84.2%和14.0%，其次是中等教育投入，为1.8%。西部地区的人力资本培育主要受自身影响，中等教育投入和经济发展水平对人力资本培育的影响基本一致。

三、主要结论及政策建议

1.主要结论

（1）中等教育投入、人力资本短期内促进经济发展

中等职业教育财政投入、人力资本培育在短期能够对经济发展产生显著的正效应。分区域看，东部地区和西部地区中等职业教育的人力资本作用不显著，中部地区中等职业教育的人力资本属性较强，对经济发展的正向作用显著，可见中部地区中等职业教育人力资本培育在较大程度上促进了区域经济发展。

（2）中等职业教育的人力资本作用具有时滞性、区域差异性

从全国看，经济发展能够为中等职业教育财政投入提供较多的资金支持，经济发展水平对中等职业教育财政投入正向影响显著。分区域看，东部地区和中部地区中等职业教育财政投入仅与其经济发展水平的一阶滞后值显著正相关，西部地区中等职业教育财政投入不仅与经济发展水平有关，还受中等职业教育人力资本培育水平滞后值的影响。因此，中等职业教育的人力资本作用不仅在时间上存在滞后性，还存在一定区域差异。

（3）经济发展水平对中等职业教育差异性影响

从全国看，经济发展水平的提高，一定程度上会导致市场对中等职业教育毕业生需求数量的减少，中等职业教育的人力资本培育水平会受到一定限制。分区域看，各地区经济发展水平和中等职业教育财政投入对中等职业教育人力资本培育的影响也存在显著差异。

（4）中等职业教育的经济增长贡献区域分布不均衡

东、中、西三大区域中，西部地区中等职业教育对经济增长的贡献最大。

2.政策建议

（1）增加专项经费投资

制定合理的生均教育经费及公用经费标准，并调整中职经费的投资力度。政府应合理调整对中职教育的专项经费投资力度，如对产业专业集群及“产学研训”一体化实训基地、现代学徒制试点及国家级1+X制度试点项目进行专项经费投资，提升中职办学条件，进而提升中职教育人才培养质量和学生就业能力。进一步调整和优化中等职业教育经费的使用效益。给予校企合作推进力度大、职业教育发展环境好、推进职业教育改革成效明显的市县经费奖励，强化中职教育经费的奖补机制。

（2）优化区域空间布局调整

首先，从区域整体性发展的视角出发，打破各区域界限，逐步确立“大区域”的发展理念，并因地制宜地制定相关政策战略。其次，提升地方政府对区域经济贡献的服务意识，通过灵活运用先进信息技术与科学预测方法，对劳动力市场上的人才需求量进行相关收集、分析及发布，并据此对中职院校的空间布局进行适当调整。