计算机自动生成数学命题——以三元均值不等式的加强为例

彭翕成 曹洪洋

(1.华中师范大学 国家数字化学习工程技术研究中心 430079；2.常州九章教育科技有限公司 213002)

数学命题是数学研究的重要部分.如果没有好的题目源源不断地“生产”出来，解题研究也难以持续发展.然而，发现一个好的命题并不容易.

设a，b，c为正数(下同)，求证：a3+b3+c3≥3abc+a(b-c)2+b(c-a)2+c(a-b)2.

这是华东师范大学《数学教学》(1985年第三期)上的一题.供题人冷岗松教授在《数学竞赛试题的若干命题策略》中讲述此题的发现经历.他给学生讲解瑞典1983年试题abc≥(-a+b+c)·(a+b-c)(a-b+c)时，一个学生采取“暴力展开”，于是有了发现.

我们简单还原一下.展开计算

abc-(-a+b+c)(a+b-c)(a-b+c)

=a3+b3+c3-a2b-ab2-b2c-bc2-a2c-ac2+3abc

=a3+b3+c3-3abc-a2b-ab2-b2c-bc2-a2c-ac2+6abc

=a3+b3+c3-3abc-a(b-c)2-b(c-a)2-c(a-b)2,

于是

abc≥(-a+b+c)(a+b-c)(a-b+c)

等价于

a3+b3+c3

≥3abc+a(b-c)2+b(c-a)2+c(a-b)2.

这一发现的过程抽象出来，即是曾经研究问题A，后来研究问题B，发现A和B之间的关联，于是得到命题C.这从侧面反映出命题之艰辛.首先是命题者需要长期积累，掌握足够多的素材，然后在接收新信息时，新老信息相互撞击，才可能有新的发现.此题若没有学生的“鲁莽”计算，发现也将擦身而过.说明命题除了需要大量积累和广泛联系，有时可能还需要一点运气.

有没有简单的方法，量产数学命题，就像现在的工农业已经实现机械化生产一样？本文将以三元算术几何均值不等式的加强为例，分享我们借助计算机探索命题的心得.

1 建立模型

由于目前的计算机还不能像人一样思考问题，所以我们需要将研究问题转化成计算机能处理的形式，或者说是将研究问题具体化：探索a3+b3+c3≥3abc+T，其中T≥0.为了使研究不致于漫无目的，需确定T的形式以及相关参数的范围，以便操作.这也是建立模型的过程.

设T=f(a,b,c)+f(b,c,a)+f(c,a,b)，f(a,b,c)=k1(a+k2b+k3c)(k4a+k5b+k6c)2，

这样所得的T是循环对称多项式，符合我们的习惯审美.而f(a,b,c)的形式是凭经验建立，并不能保证这样形式的T一定存在，还需试验检验.如不要求T是循环对称式，或是放开参数的范围，可得到更多的T.

根据乘法原理，T的可能取值为3×5×5×5×5×5=9375个，远超过人工所能处理的范围.由于变量实在太多，即使借助计算机，解不等式a3+b3+c3≥3abc+T≥3abc也颇为不易.我们此处不解不等式，而是搜索验证给定范围内符合要求的T.下面借助符号计算软件Mathematica来进行处理.

2 数据分析

对于可能的9375个T，每一个T都对应着不等式a3+b3+c3≥3abc+T≥3abc.这其中绝大多数T不符合要求.而排除不合要求的T，最直接的方式就是举反例.

筛选数据计算机随机生成一组正数，赋值给a,b,c，并对9375个不等式a3+b3+c3≥3abc+T≥3abc进行验证，可排除部分T.对这一操作重复执行3000次，能通过数值验算的T只有几十个.

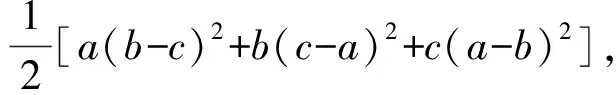
如a(b-c)2+b(c-a)2+c(a-b)2与a(c-b)2+c(b-a)2+b(a-c)2，看似有差别，实则一样，保留一个即可.最后，我们选取如下8个.

a2(a-b)+b2(b-c)+c2(c-a)……(t7)，

a(b-c)2+b(c-a)2+c(a-b)2……(t8).

3 证明检验

特例法，我们日常解题时也经常用，只不过人工举例，特例的个数少，可能出错的可能性就大.而利用计算机的快速计算，经过上千次的检验，错误的可能性就低.因此所得的8个T，大概率保证是符合要求的.为进一步检验这些不等式的正确性，我们将GroebnerBasis算法加以改进，让计算机自动生成多项式之间的关系式，也就是将要求证的关系式改写成若干非负项之和：

对于t1，不妨设c=min(a,b,c)，

a3+b3+c3-3abc

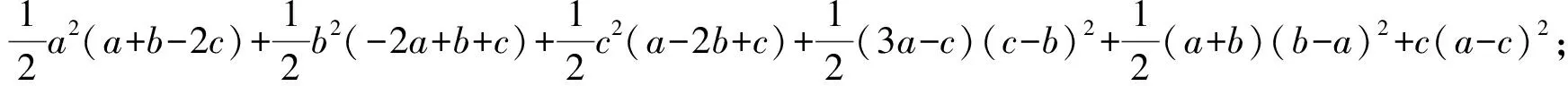
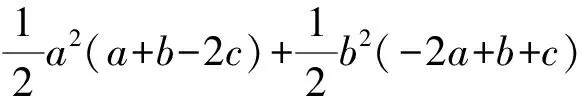
因此a3+b3+c3≥3abc+t1≥3abc得证.

对于t2，

a3+b3+c3-3abc

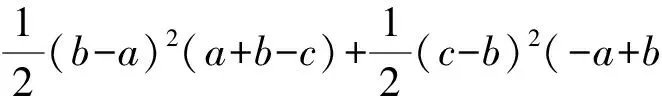
+b(a-c)2+c(b-a)2；

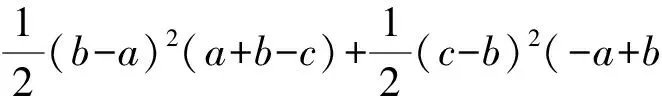
=a(a-b)(a-c)+b(b-a)(b-c)+c(c-a)(c-b)(舒尔不等式形式)；

因此a3+b3+c3≥3abc+t2≥3abc得证.

对于t3，

a3+b3+c3-3abc

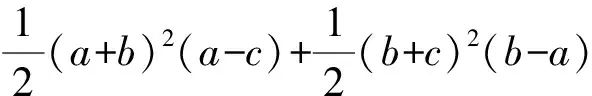
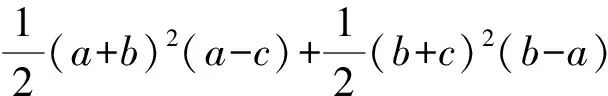
因此a3+b3+c3≥3abc+t3≥3abc得证.

对于t4，

a3+b3+c3-3abc

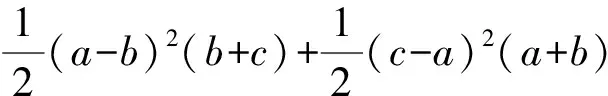
因此a3+b3+c3≥3abc+t4≥3abc得证.

剩余4式，证法基本类似，留与读者证明.

4 直观显示

一次得到多个结论的同时，又有新问题冒出，即所得这些T之间的相互比较.首先要注意存在两个T无法比较的可能.譬如t1和t2.

当a=1，b=1，c=2时，

当a=2，b=1，c=2时，

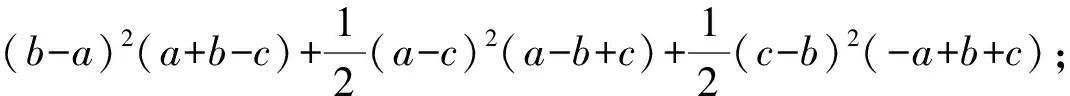
所以t1和t2之间不可比较.

我们仍采用数值检验方法.从T中任选两项ti和tj，计算得到ti-tj的正负号，随机对a,b,c赋值，重复执行3000次.若1000次结果都为非负，输出ti≥tj；若3000次结果都为非正，输出ti≤tj；其余情况，则不输出.

为了更直观地显示，有必要借助图论中有向图的概念，将一个T看成一个点，若ti≤tj，则ti→tj，即生成一条有向边，不等式中较小的项指向较大的项，于是可得到一个不等式的关系图(图1).正如上文所说，t1和t2之间不可比较，因此两者之间无边相连.另外，t6,t8不在图1中，说明这两个T互相之间不可比较.

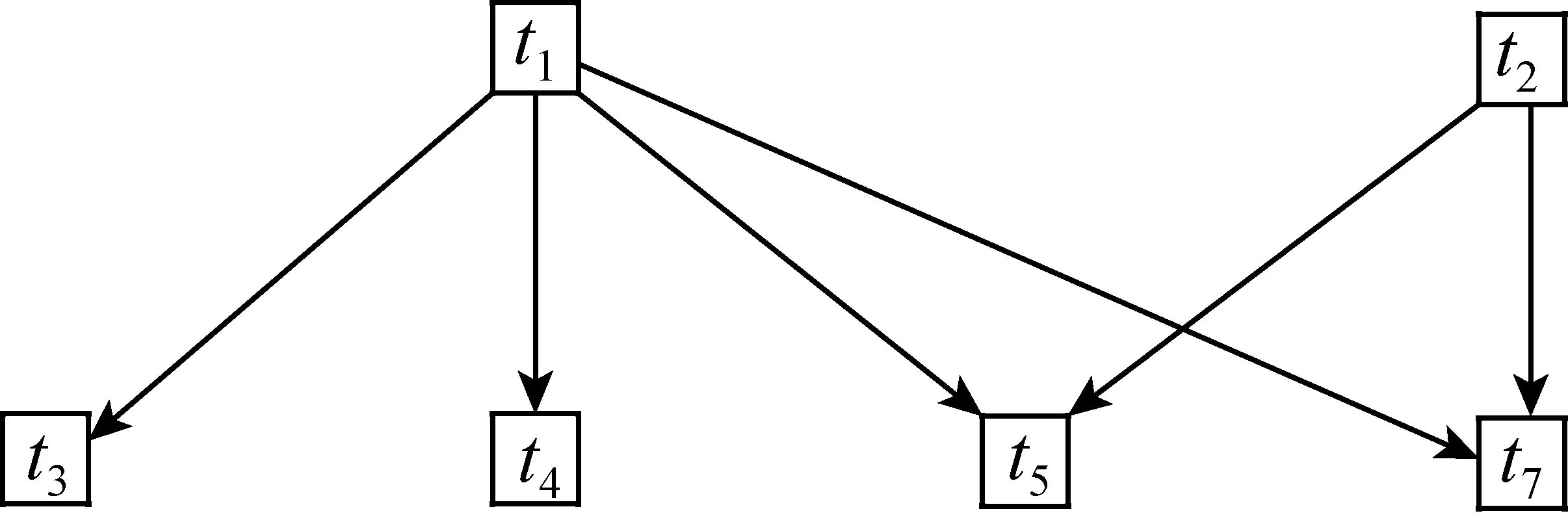
图1

如果设a3+b3+c3……(t9)，3abc……(t10)，重新生成不等式关系图(图2).因为多了可比较对象，因此t6,t8在图2中出现.显然t9最大，而t10与t1～t8无法比较强弱.

至此，我们通过建立模型、分析数据、证明检验、直观显示四个步骤，探索了三元均值不等式的加强，所得的结论可为教学、考试、研究等提供素材.本文研究如果单靠人工，需花费较多时间.而这样的工作量对于计算机则是小菜一碟.在考虑成熟，建立合适的模型以及编写好程序之后，计算机输出8个T以及作图1、2，总共无需2分钟，这样就能把节省下来的时间投入到更有创造力的研究中去.

莱布尼兹认为，一个出色的人像奴隶一样把时间浪费在计算上是不值得的.如果有了机器，这种工作可以放心地交给任何人.意思是不要把时间浪费在加减乘除这样烦琐的脑力劳动上.推而广之，还有哪些脑力劳动可以让计算机来帮助完成？吴文俊先生认为这其中大有可为.工业革命是使用某种机器来减轻甚至代替体力劳动，现在是信息技术时代，可利用计算机来减轻甚至代替脑力劳动.计算机对于数学家，势将与显微镜对于生物学家，望远镜对于天文学家那样不可或缺.计算机提供了有力工具，使数学有 可能像其他自然科学一样，跻身科学试验行列.

目前初等数学的研究，主要还是纸笔手算.大数据时代，数学建模和数据分析已成为中学数学需要培养的核心素养.能否针对要研究的初等数学问题建立数学模型，并借助计算机进行数据计算和分析，批量处理一类问题？本文的探索表明，完全可行.同时本文也为中学数学建模提供了参考案例.由于中学生知识水平、投入精力等多方面的限制，研究一些生活、生产问题存在多方面的困难，而研究初等数学内部的一些问题可能更具有可操作性.