溯教材之源 探高考之变 究实验之道
——从教材的一道习题说开去
2022-07-12孙韩玉
孙韩玉
(安徽省滁州中学 239001)
数学教材为学生的学习活动提供了主题、基本线索和知识结构,是实现数学课程目标、实施数学教学的重要资源[1].同时,教材也是制定教学大纲和高考考试大纲的基本依据.罗增儒教授曾指出:“教材是课程的载体,所以高考命题最具体、最方便的依据其实就是教材.”历年高考试题中都有一些题目源于教材而又高于教材,它既能体现考试公平,又能考查教学成果,具有鲜明的教学导向.因此,对一道教材习题的深度拓展与开发,抽象其数学本质,形成其知识体系,发挥其教育价值,这对于更好地培养数学思维和发展数学核心素养有着重要的意义.
1 溯教材之源——见山是山
高中人教A版数学课本选修2-1第49页第7题:如图1,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点.线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?[2]

图1
由垂直平分线的性质可知,|QP|=|QA|,所以|QO|+|QA|=|QO|+|QP|=|OP|,而|OP|是圆O的半径r为定值且大于|OA|,故点Q的轨迹是以O,A为焦点的椭圆如图2.

图2
数学家波利亚曾形象地说:“好问题同某种蘑菇相像,它们成堆生长,找到一个以后,你应当在周围找找,很可能附近就有几个.”这道课本上的例题就如同“蘑菇”一样,我们可以改变点A的位置,依然研究线段AP的垂直平分线l和半径OP的交点Q的轨迹,那么点Q的轨迹又会是什么呢?考虑到点与圆的位置关系,下面分别来研究当点A在圆内(与圆心O重合)、圆上、圆外时的点Q的轨迹.

当点A在圆外时,线段AP的垂直平分线与半径OP无交点,为了能继续研究,我们这里研究线段AP的垂直平分线与半径OP所在的直线的交点,这样点Q便可以画出.同样由垂直平分线的性质可知|QP|=|QA|,所以|QA|-|QO|=|QP|-|QO|=|OP|=r<|OA|,故点Q的轨迹是以O,A为焦点的双曲线的左支,如图3.当移动点P时,此时又有|QO|-|QA|=|QO|-|QP|=|OP|=r<|OA|,故点Q的轨迹是以O,A为焦点的双曲线的右支,如图4,综上,点Q的轨迹是以O,A为焦点的双曲线.
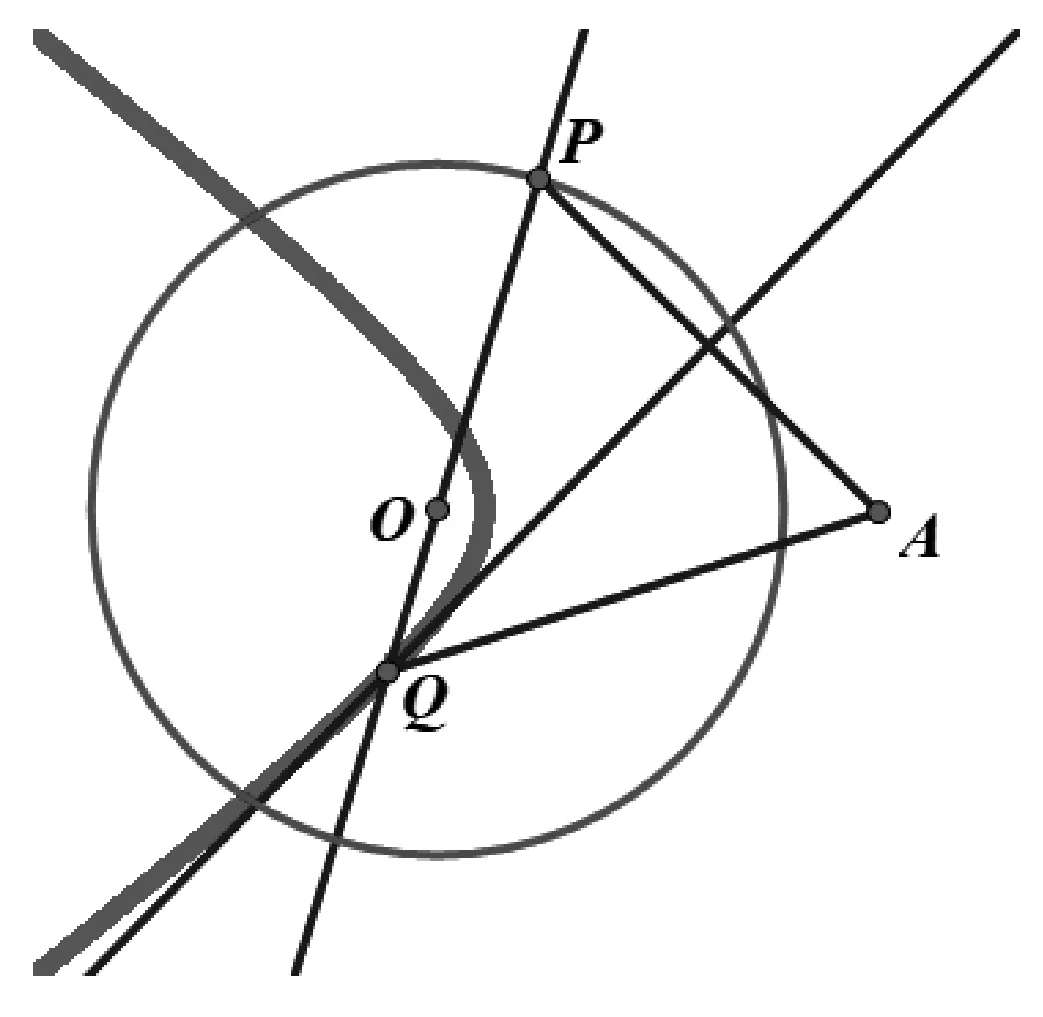
图3
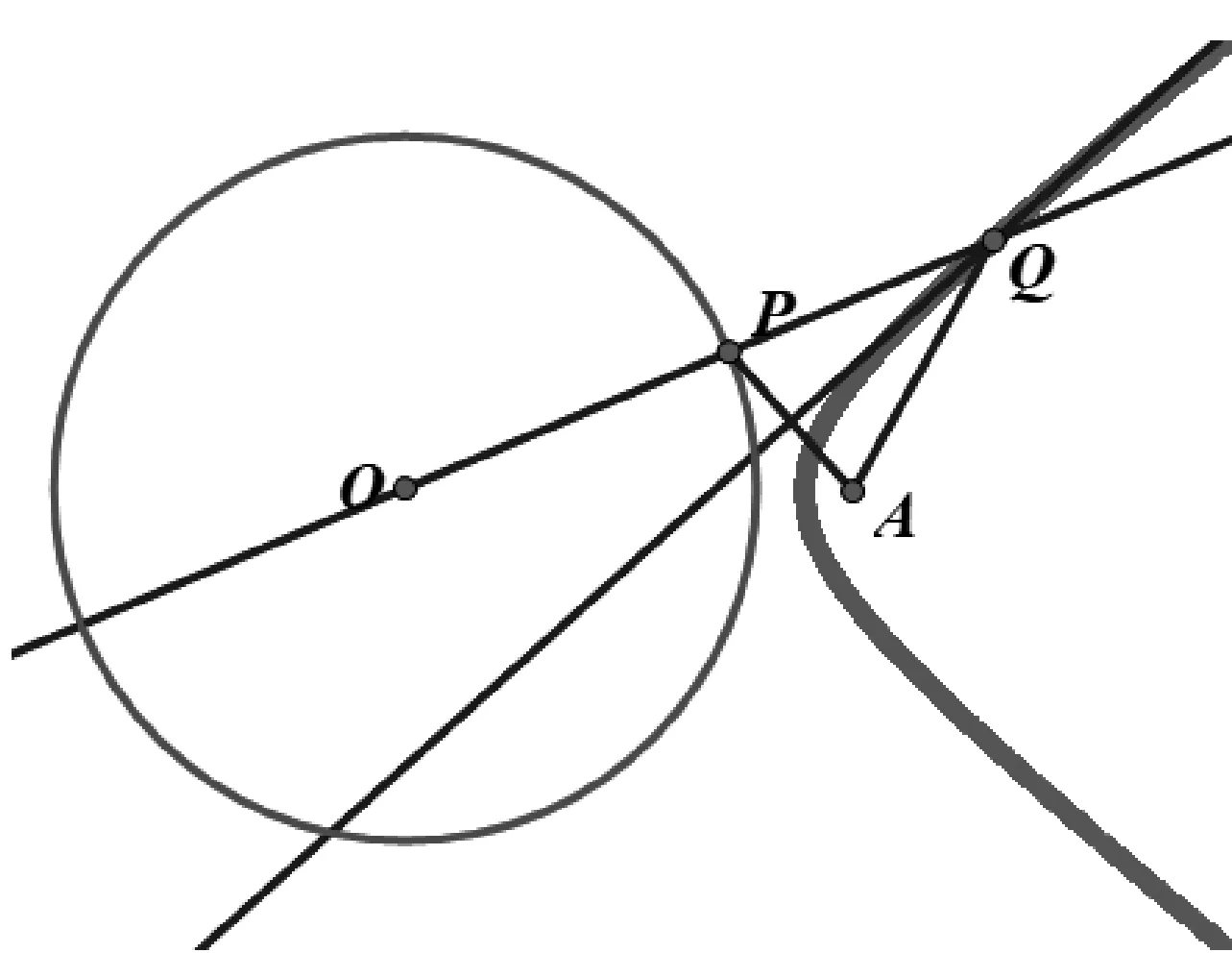
图4
2 探高考之变——见山不是山
在图1的基础上,如果我们把PA延长与圆交于点M,连接OM,QA,因为QP=QA,所以∠QAP=∠QPA,又因为OP=OM,所以∠OPA=∠OMP,故∠QAP=∠OMP,于是QA∥OM,如图5,从而由“线段AP的垂直平分线l和半径OP相交于点Q”可推出“QA∥OM”,显然其逆命题也成立,故可以把课本习题改头换面为:A是半径为r的圆O内一个定点,过点A的直线l与圆O交于P,M两点,过点A作OM的平行线交OP于点Q,则点Q的轨迹是什么?

图5
以上基于课本习题的改编和2016年全国I卷理科第20题第(1)问如出一辙:设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E,如图6. 证明:|EA|+|EB|为定值,并写出点E的轨迹方程.(过程同上,此处省略)

图6
学生可能做过课本上的习题,但这道改编后的高考题却给学生一种“见山不是山”的新鲜感,由此可见,一些高考题源于教材而又高于教材.由图3可知,当点A在圆外时,点Q的轨迹为双曲线,故将这道高考题尝试作以下改编,希望对后续备考作一些参考意义,改编如下:设圆x2+y2+2x=0的圆心为A,直线l过点B(1,0)交圆A于C,D两点,过B作AC的平行线交AD于点E. 求点E的轨迹方程.
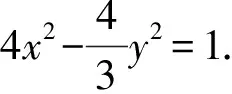

图7

图8
本道改编题较原高考题增加了不少难度,这是因为学生可能会忽视对另外一种情况的讨论,从而得到的轨迹只是双曲线的一支,这恰恰是学生的一个易错点和难点,所以本道改编题在轨迹专题复习中具有很好的警示作用,它不仅能考察双曲线的定义,还能培养学生思维的严密性.
3 究实验之道——见山还是山
数学教育家弗赖登塔尔在《作为教育任务的数学》一书中指出:“将数学作为一种活动来进行解释和分析,建立在这一基础上的教学方法称之为再创造方法”[3].弗赖登塔尔认为“学习数学的唯一正确的方法就是实行‘再创造’”.数学教师要引导学生进行这种再创造的活动,数学实验就是一个很好的抓手,它能让学生在做数学的过程中培养自己的思维能力和创新能力.为此,在图1探究点Q轨迹的基础上,在课堂上开展如下数学实验,从而深化对椭圆概念的理解:
①先准备一个圆形纸片,在纸片内部确定异于中心点O的一点F,如图9;

图9
②开始折叠圆,将圆折起一角,使得圆周正好过点F,此时产生了一条折痕L,如图10;

图10
③重复上述过程继续折下去,将得到若干条折痕,将每一条折痕都用笔标记出来,仔细观察,这些折痕围成了一个什么图形,如图11,你能解释其中的原理吗?

图11
问题1圆周上与F重合的点记为M,F和M具有怎样的位置关系,折痕可以看作是F和M的什么?
学生不难发现F和M关于折痕L对称,折痕实为F和M的垂直平分线如图12,当点M在圆上运动时,折痕会随之而动.接下来教师再用GeoGebra对折痕进行动态演示,学生会发现折痕围成了一个椭圆如图13.

图12

图13
问题2我们知道点动成线,折痕作为一条直线为什么能围成一个曲线呢?
引导学生从本质上把握曲线形成的原因:点运动的轨迹.从而把关注点转移到折痕上某个点所形成的轨迹.
问题3我们可以利用什么来判断动点的轨迹是椭圆呢?
学生不难想到利用椭圆的定义,教师让学生复述定义的具体内容即平面内到两定点的距离之和为定值(大于两定点间的距离)的点的轨迹为椭圆,再一次明确定义中的关键要素:一个动点、两个定点、和为定值.
问题4定义中涉及到一个动点和两个定点,折痕上的点是我们研究的动点,图中哪些是定点呢?
圆心O和圆内一点F为两个定点,这为研究动点到这两定点的距离之和为定值做好方向性的指引.
问题5说到定值,你觉得圆里面哪个量是不变的呢,由此,你想到连接哪条线了吗,你可以找到那个点了吗?
由于圆中半径是定值,学生不难想到连接OM,此时OM与折痕交于点P,如图14,由垂直平分线的性质可知|PM|=|PF|,于是再结合两个定点便有|PO|+|PF|=|PO|+|PM|=|OM|,且|OM|>|OF|,故P的轨迹是以O和F为焦点的椭圆,最后教师再通过GeoGebra的动态演示让学生直观的感受折痕围成的椭圆就是折痕上的点运动的轨迹,如图15.

图14

图15
以上过程可以总结为:重复折叠纸片——圆周点M运动——折痕直线运动——点P运动——形成椭圆.在这个过程中,学生需要把“折叠圆使得圆周正好过点F” 抽象为“折痕为F和M的垂直平分线”;然后在已有垂直平分线性质和椭圆定义的基础上进行分析,推理出折痕上某个点到两定点的距离之和是定值.本实验其实就是教材习题所蕴含的一个动手实践,过程中处处体现着数学抽象和逻辑推理.学生看过了以前的“山”即图1点的运动轨迹,再去看现在的“山”即折纸实验,就会有一种“看山还是山”的顿悟和喜悦,从而揭示出该问题的数学本质.
由于该实验的原理就是出自于图1,我们可以让学生根据图2自己设计一个折纸实验——折双曲线:①先准备一张A4纸,在纸上画一个圆,在圆的外部确定一点F;②开始 折叠圆,将圆折起一角,使得圆周正好过点F,此时产生了一条折痕L;③重复上述过程继续折下去,将每一条折痕都用笔标记出来,这些折痕就围成了一个双曲线.
行文至此,对教材这道习题的开发似乎可以拉下帷幕了,但真的就没有遗珠了吗?事实上,还有一些问题有待深挖,如从纵向的角度来看,在探究点Q轨迹的过程中,通过改变点Q的位置,我们可以得到圆、椭圆、双曲线,但唯独没有圆锥曲线中的抛物线,似乎有些遗憾,我们知道数学是追求和谐与统一的,那如何通过类似的操作得到抛物线呢?又如从横向的角度来看,除了教材习题呈现圆锥曲线的方式,还有哪些作法可以得到圆锥曲线的轨迹呢?限于篇幅,这里就不再详细探讨,留给读者思考.
结束语
我国著名的教育家叶圣陶曾说:“教材无非是个例子,它只能作为教课的依据,要教得好,使学生收益,还要靠教师善于应用.”本文通过深耕教材上的一道习题,开启了一段探高考之变、究实验之道的智慧之旅,将书本上“冰冷的美丽”转化为学生“火热的思考”.在高三复习备考的过程中,希望越来越多的教师能创造性地使用教材和整合资源,带领学生跳出题海,回归教材,正所谓“众里寻他千百度,蓦然回首,那人却在灯火阑珊处”.
