接收函数界面和波速成像研究进展与展望

陈 凌，王 旭，王 新，危自根，张建勇

1 中国科学院地质与地球物理研究所 岩石圈演化国家重点实验室，北京 100029

2 中国科学院大学地球与行星科学学院，北京 100049

3 中国科学院地质与地球物理研究所 地球与行星物理重点实验室，北京 100029

4 中国科学院精密测量科学与技术创新研究院 大地测量与地球动力学国家重点实验室，武汉 430077

5 中国地震台网中心，北京 100045

0 引言

结构分层性，是在地球径向上被物理和/或化学性质随深度强烈变化的若干界面所分隔形成的圈层结构，是地球最基本的特征之一（Dziewonski and Anderson,1981）.对地球圈层结构的研究，是认识地球内部物质组成与性质、探索板块构造及地球系统动力运行机制和过程的基础（滕吉文，2001,2008；徐义刚等，2022），其关键在于对分隔圈层的各界面基本结构、性质和成因开展探测研究.研究地球内部界面结构常用的地震学方法有：深地震反射、接收函数、SS/PP前驱波、ScS多次反射波、三重震相、以及近源sdP转换波等信号的分析和成像（Langston,1979;Revenaugh and Jordan,1991;Shearer,1999;White et al.,2003;Song et al.,2004;Li et al.,2008;Duess,2009;Schmerr,2012;Gao et al.,2016;Lai et al.,2019）.其中，人工源深地震反射方法震源能量小，观测距离短，探测成本高，难以用于长尺度和地幔界面结构成像研究；在基于天然地震资料的方法中，长周期SS前驱波、ScS多次反射波方法因其对地震台站与震源中间区域的界面结构敏感，对约束台站稀疏布设的大洋下方的界面结构有重要意义；但由于SS前驱波和ScS 多次反射波主频较低，该方法获得的地球内部界面结构横向和纵向分辨率有限，往往用来构建大尺度甚至全球尺度界面结构.三重震相波形拟合方法和近源sdP转换波叠加方法的优势在于利用较高频的地震波约束界面小尺度精细结构，但其应用范围受限于地震和密集台阵的空间分布.接收函数则主要是针对台站下方精细界面结构研究而提出并发展的天然地震资料成像方法，目前已成为地壳和上地幔界面及相关波速结构成像的最常用地震学研究手段之一.

接收函数（Receiver Function,RF）是指去除震源函数、地震波传播路径以及仪器响应等因素后的远震时间域波形序列，记录了地震台站下方壳幔波速界面对地震波的响应（Phinney,1964;Vinnik,1977;Langston,1979）,可用于提取界面及其之上的结构（速度、泊松比、各向异性等）信息.Phinney（1964）通过模拟远震P波垂直和径向位移分量振幅谱的比值来推测台站下方的地壳结构，被认为是最初的接收函数思想.Vinnik（1977）最早从远震体波波形中去除震源函数和传播路径响应，提取了台阵下方410-km和660-km界面的区域平均响应.Langston（1979）提出等效源函数概念，在平面波入射和近垂直入射假设条件下，从远震体波尾波中分离出台站下方介质对入射P波的脉冲响应，首次从单台长周期远震体波记录中提取出了接收函数.Owens等（1984）发展了宽频带接收函数频率域反褶积提取方法.此后，接收函数方法得到了快速发展和广泛应用.

自接收函数最初思想诞生的半个多世纪以来，对接收函数方法从理论到实际应用的研究主要围绕三个方面开展：接收函数的有效提取、界面结构成像方法的发展与应用、波速结构成像方法的发展与应用.本文将在介绍接收函数原理基础上，分别对上述三个方面的研究进行梳理，重点介绍近20年以来的研究进展，提出仍存在的问题及可能的解决思路.最后从方法突破和应用前景两个角度，探讨接收函数研究的未来发展方向.

1 接收函数原理和方法

1.1 P波和S波接收函数

接收函数分为P波接收函数（P-RF）和S波接收函数（S-RF）两种类型，分别对应远震P波和S波入射情况下，壳幔界面产生的Ps和Sp转换波以及地表反射产生的多次波（图1，表1）.其中，P波接收函数频率范围广（～0.1 Hz至1 Hz以上），利用界面Ps震相的走时和/或振幅信息，或结合相应的多次波（PpPs,PsPs+PpSs）特征，能够约束从地壳到地幔过渡带、甚至下地幔顶部的界面结构（如，Dueker and Sheehan,1997;Ai and Zheng et al.,2003;Zheng et al.,2006;危自根等,2021）.然而，上地幔浅部界面的Ps转换波震相易受地壳强界面、特别是Moho面多次波的干扰（图1b），因此P波接收函数方法在～50～200 km深度包括岩石圈地幔和软流圈顶部范围的界面成像方面存在困难；与P波接收函数相比，S波接收函数由于S波到时较晚、受P波尾波干扰而信噪比较低，而且频率也相对较低（通常＜0.5 Hz），因而分辨能力较弱，难以有效约束地壳尺度的界面结构.S波接收函数的优势在于，Sp转换波与多次波分别早于和晚于直达S波到达台站，从而分列于S波接收函数时间轴（以直达S波到时为零时刻）的两侧（图1d），因此Sp转换波不受多次波干扰.这一特点使S波接收函数适宜于对P波接收函数成像困难的上地幔浅部界面，如岩石圈—软流圈边界（lithosphereasthenosphere boundary,LAB）、岩石圈内部界面（mid-lithosphere discontinuity,MLD），以及软流圈中可能的界面开展研究（如，Farra and Vinnik,2000;Chen et al.,2014;Mark et al.,2021;Wu et al.,2021）.基于P波接收函数和S 波接收函数对壳幔结构的不同敏感性特征，将两者联合进行分析，可以获得更为丰富和全面的地壳—上地幔结构信息（如，Rychert et al.,2007;Chen,2009;Abt et al.,2010;Chen et al.,2014;Bissig et al.,2021）.

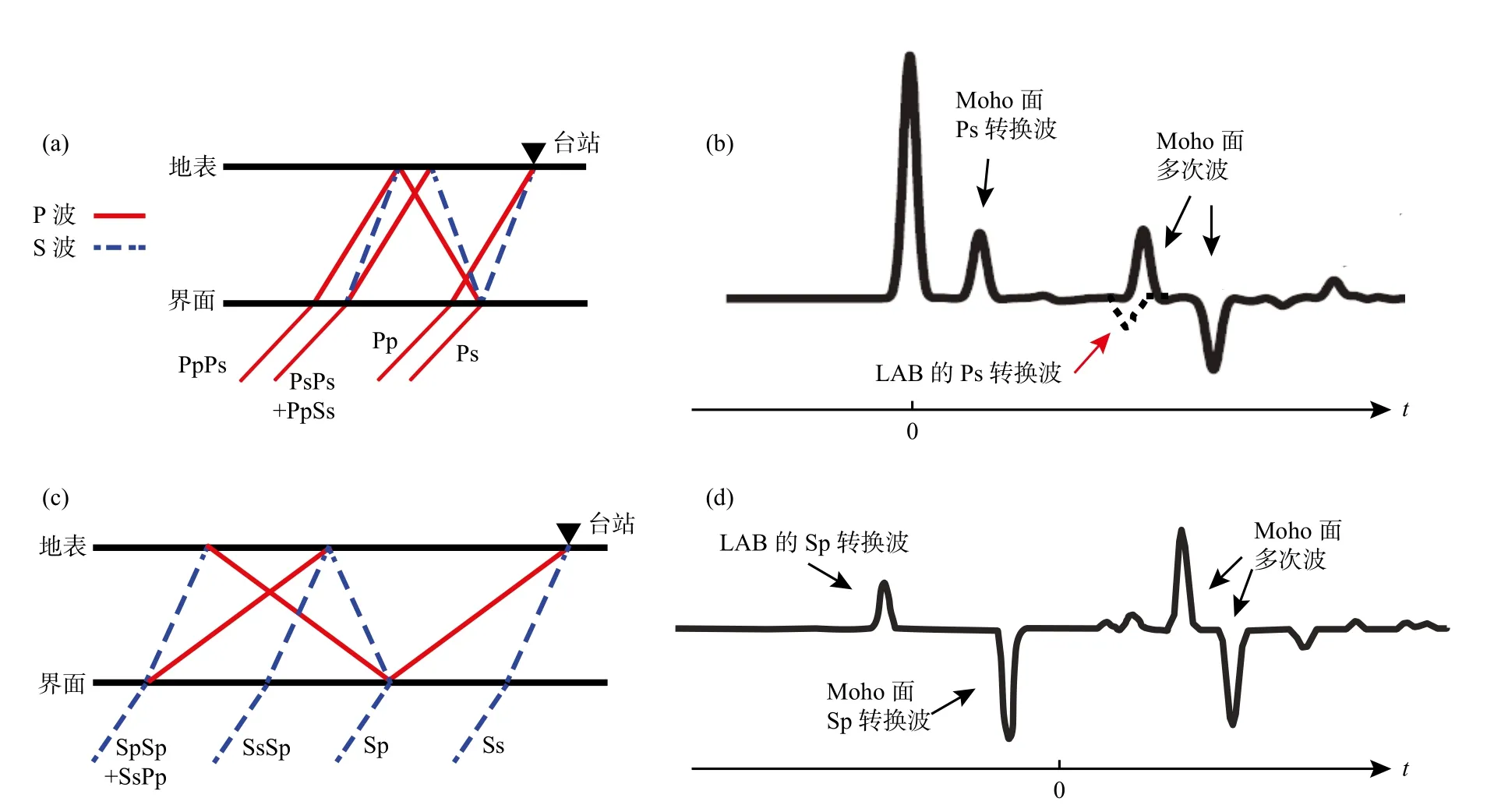
图1 P波和S波接收函数示意图.（a，b）Ps转换波及其多次波震相传播路径与理论P-RF示例；（c，d）Sp转换波及其多次波震相传播路径与理论S-RF示例Fig.1 Schematic diagrams showing the P-wave and S-wave receiver functions (P-RF and S-RF).(a,b) Ray paths of Ps conversion and multiples and a theoretical P-RF time series;(c,d) Ray-paths of Sp conversion and multiples and a theoretical S-RF time series

表1 P波接收函数和S波接收函数的基本参数、方法及应用特征对比Table 1 Comparison of basic parameters,method and application characteristics of P-wave and S-wave receiver functions

鉴于P波接收函数应用更为普遍，本文后续除非特别说明，接收函数均指P波接收函数，而且主要指径向P波接收函数.

1.2 提取接收函数的反褶积方法

P波和S波接收函数的提取，关键是要从地表台站的远震记录中去除震源函数、地震波传播路径以及仪器响应等影响，获得台站下方波速界面对入射P波或S波的响应.以P波接收函数为例，对于层状地球模型，地表台站下方的远震入射波场可采用平面波场来近似.台站记录的三分量远震P波波形在时间域可表示为仪器响应、震源时间函数和介质结构响应的褶积（Langston,1979），即：

其中D(t)表 示地表台站的远震P波波形记录，I(t)表示仪器脉冲响应，S(t)表示入射平面波的有效震源时间函数，包含震源和入射前远震路径效应，E(t)表示介质结构响应，下标V、R、T分别表示垂直、径向和切向分量.理论计算与实际观测表明，远震P波波形的垂直分量主要由直达波构成，其续至波能量较弱（可忽略不记），从而EV(t)可近似看为脉冲函数.因此，远震P波径向和切向分量可表示为：

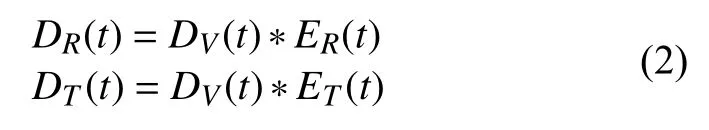
其中ER(t)、ET(t)分别称之为径向和切向接收函数。由于D(t)已知,接收函数的提取实际是一个反褶积运算，通过水平分量对垂直分量的反褶积分离出台站下方介质结构响应.

提取接收函数的反褶积运算可在频率域或时间域进行.在频率域进行反褶积时，由于实际地震信号具有有限带宽，且包含随机噪声，垂直分量的频谱常含有近零成分，从而导致频谱相除的不稳定，因此常采用“水准量”（即分母最小值）来压制近零值频谱.水准量反褶积避免了极小垂直谱振幅所造成的计算不稳定性，采用高斯滤波则进一步消除了高频噪声（Langston,1979）.频率域内水准量反褶积方法提取接收函数简单便捷、计算效率高，但其固有缺点在于引入水准量的同时也降低了精度，且不可避免地压制了能量较弱的转换波震相，特别是上地幔深部界面的微弱震相.Owens等（1984）将这种频率域反褶积方法从最初分析世界标准地震观测网（WWSSN）长周期数据拓展到应用于宽频带地震记录，并用以反演地壳S波速度结构；Ammon（1991）进一步改进了接收函数提取方法，对径向接收函数的绝对振幅进行有效估计，同时改善了接收函数线性反演的非唯一问题.此后，多种其它频率域反褶积方法也陆续被提出以提高接收函数的稳定性和精度，如单台复谱比方法（刘启元等，1996）、多道最大或然性反褶积方法（刘启元和Kind，2004）、多重镶窗接收函数提取方法（Park and Levin,2000）以及多正弦窗接收函数提取方法（司少坤等，2014）等.

时间域反褶积方法通过时间域波形对比设定目标函数来提取接收函数.时间域反褶积运算的优点较为直观，其数据长度和滤波因子长度灵活可变，而且也不需要设定类似频率域中的水准量，缺点是计算效率相对较低.时间域反褶积提取接收函数可以通过最小均方误差准则下的维纳（Wiener）滤波来实现（Gurrola et al.,1995）.该方法将远震P波垂向分量与接收函数褶积得到的维纳滤波器实际输出与远震P波径向分量做对比，以两者波形均方误差达到极小作为提取接收函数的准则，其本质是Toeplitz方程的求解.为了进一步提高接收函数提取的精度和稳定性以及计算效率，迭代求解反褶积（Ligorria and Ammon,1999）、最大熵谱反褶积（吴庆举等，2003）、多道滤波反褶积（吴庆举等，2007a）以及考虑稀疏时间序列和噪声特征的贝叶斯概率统计反褶积（Yildirim et al.,2010；Kolb and Lekić,2014）等时间域接收函数提取方法相继得到发展.

频率域和时间域反褶积提取接收函数的方法各有优缺点，在实际数据处理中存在不同程度的差异.图2展示了两个典型台站（大兴安岭山地基岩台、厚沉积层松辽盆地台）采用目前主流的频率域和时间域反褶积方法提取的接收函数波形.可以看出，无论是山地基岩台还是厚沉积层盆地台，同一地震事件数据不同反褶积方法计算的接收函数均存在差别（图2a、2b），特别对于盆地台差别更为显著（图2b）.这一现象反映了反褶积计算内在的非唯一性（intrinsic non-uniqueness of deconvolution），尤其对于结构变化复杂、强烈的区域（如盆地地区），反褶积结果具有更大的不稳定性（图2b）.通过多个地震事件接收函数的叠加能够减小不同方法计算结果的差别（对比图2c、2d与图2a、2b），因此多事件接收函数叠加是目前降低反褶积不稳定性、提取台站之下可靠结构信息的主要方式.然而对于厚沉积层盆地台，其强烈的结构垂向变化以及各向异性等因素影响了叠加的有效性（图2d），需要更多事件的接收函数进行叠加来提高稳定性.

1.3 提取接收函数的台阵算法

接收函数的提取是一个不同地震波形分量之间的反褶积过程，原理简单，但难点在于如何克服反褶积的内在非唯一性（如图2所示），提取稳定、可靠的接收函数.特别对于短周期节点地震仪观测的接收函数研究，存在频率高、波形噪声水平高，记录的远震事件少（观测周期短）、叠加不足等问题，如何充分、有效利用短周期节点地震仪密集观测进行高精度接收函数提取和结构成像，仍极具挑战性.

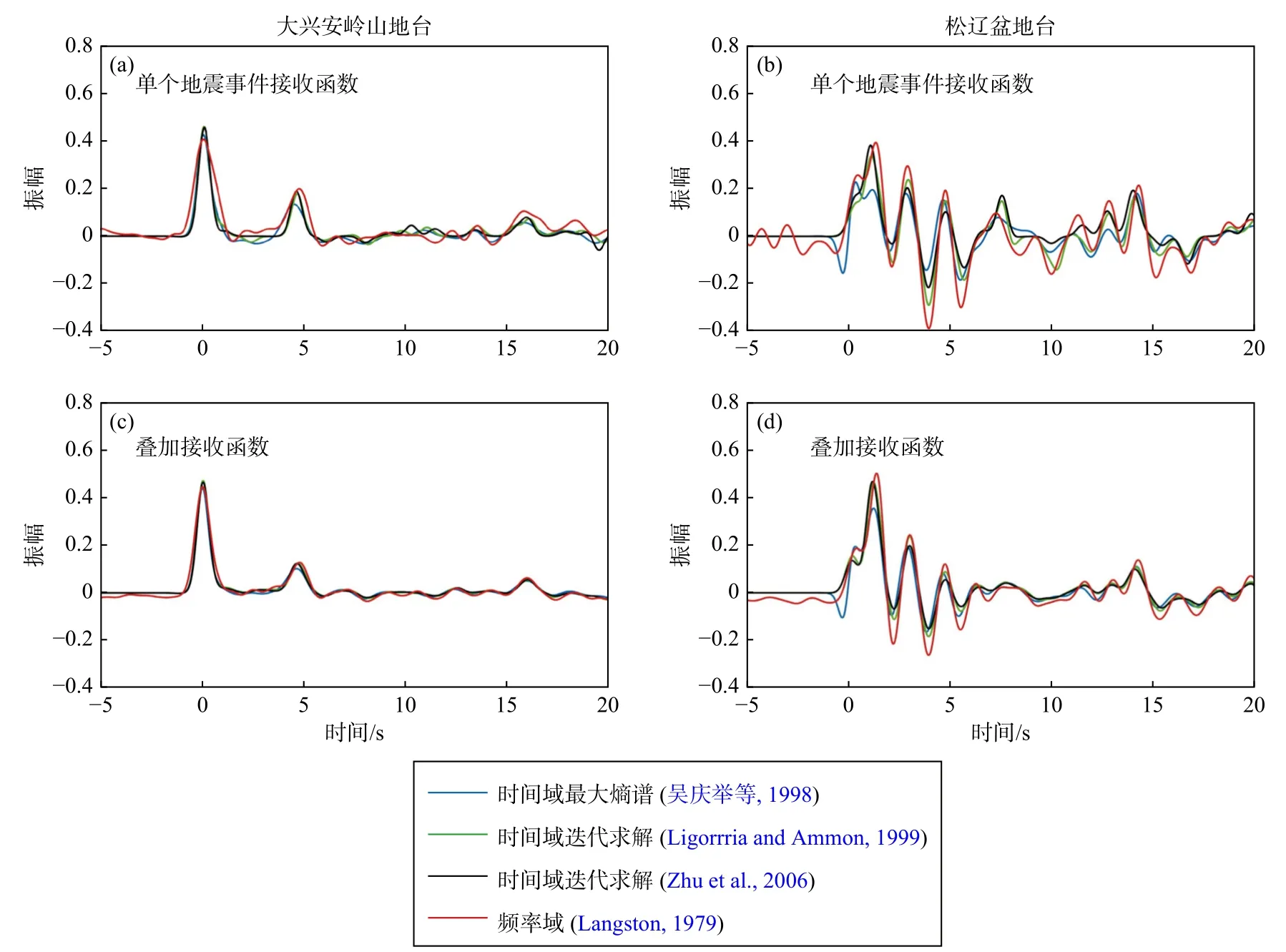
图2 不同反褶积方法提取的P波接收函数对比.（a，c）分别为一大兴安岭山地台站单个事件和32个事件叠加的接收函数；（b，d）分别为一松辽盆地台站单个事件和49个事件叠加的接收函数Fig.2 Comparison of P-RFs calculated by various deconvolution methods.(a,c) Single-event and 32-events-averaged P-RFs for a station located on the bedrock in the Daxinganling area;(b,d) Single-event and 49-events-averaged P-RFs for a station located in the Songliao Basin

针对目前快速发展的密集台阵观测技术，Zhong和Zhan（2020）发展了基于密集台阵的相干接收函数算法（array-based coherent receiver functions）.该方法利用密集台阵连续波场记录，引入相邻台站接收函数的震相相干思想，通过同时反演多地震、相邻台站的波形记录，来提取台阵接收函数（图3）.相对于传统“单地震—单台站”接收函数而言，该方法通过密集台阵数据的联合反演有效抑制了非相干噪声和局部散射，显著降低了单台反褶积的非唯一性和数据的过度拟合性.然而，由于采用非线性邻域反演算法，该方法计算效率较低，且人为选取接收函数“最优”震相的数目基于一定的基本假设，其合理性有待证明.考虑到上述优缺点，Wang等（2021a）进一步发展了适应于密集台阵的变维贝叶斯相干接收函数算法.变维思想的引入，有助于避免人为选择震相数目带来的不确定性；而贝叶斯概率统计方法的引入，有助于使用后验概率信息估算接收函数误差，进而进行更定量的地质解译.此外，该算法使用并行计算求解，有效提升计算效率.

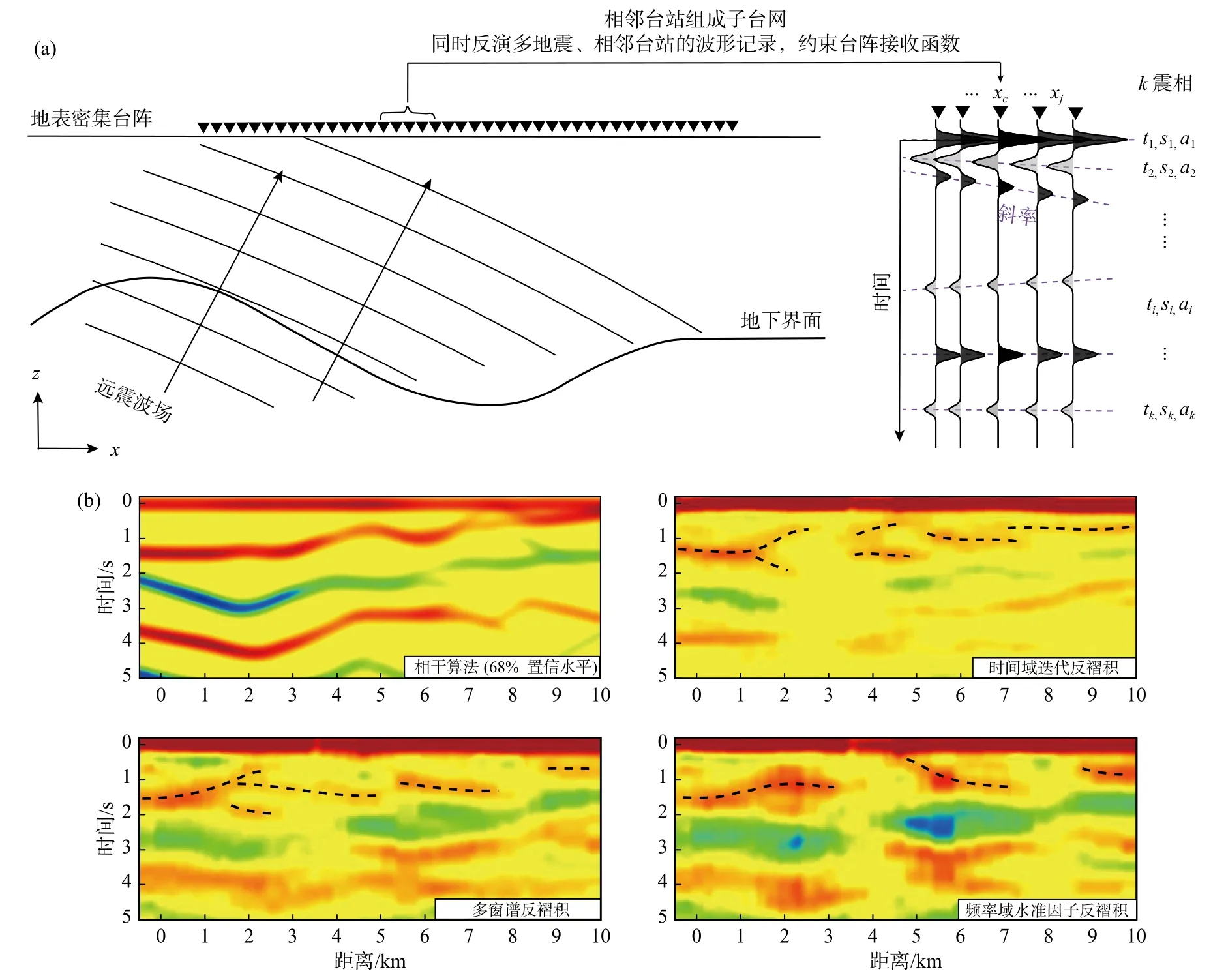
图3 基于密集台阵的相干接收函数算法与实际应用（修改自Wang et al.,2021a）.（a）算法示意图.间距较小的相邻台站下方结构往往具有一致性，因此可以通过多地震、相邻台站联合反演有效抑制地下非相干噪声和局部散射，提高反褶积的稳定性.右图为包含5个相邻台站子台网的相干接收函数.紫色虚线表示相干接收函数震相，每个震相由相对到时t、慢度s 和振幅a三个参数表示.（b）应用于台间距约250 m、观测时间1个月的密集台阵资料，相干接收函数（可靠度大于68%的震相）与三种常用方法计算的“单台站—单地震”接收函数对比，其中黑色虚线为根据成像结果识别的盆地沉积—基底界面.由于反褶积方法的非唯一性及有限观测时间造成的叠加不足，不同常用方法获得的盆地结构存在差异Fig.3 Schematic illustration of the array-based coherent receiver function (CRF) algorithm and its application (modified from Wang et al.,2021a).(a) Schematic illustration of the CRF algorithm.Due to the close station spacing,the sub-surface structures at nearby stations commonly share similar features.Thus,the deconvolution at a single station can involve the constraints from the nearby stations and multiple earthquakes to effectively suppress noncoherent noise and local scatterings,to improve the reliability of RF estimation.The right panel shows the CRF for a sub-network including five neighboring stations.Purple dashed lines indicate CRF phases,each of which is represented by three parameters:relative arrival time,slowness,and amplitude.(b) Comparison of the performance of CRF (phases with reliability ＞68%) with the traditional "single-station-singleevent" RF deconvolution methods for a dense array with a station spacing of～250 m and an observation period of one month.Black dashed lines are inferred sediment-basement interfaces based on the imaging results.Due to the non-uniqueness of the deconvolution and the insufficiency of the data for stacking due to the limited observation period,the basin structures obtained by the three different conventional methods differ considerably from each other

台阵接收函数思想和方法（图3）的提出打破了传统将接收函数研究视为“收集数据”的观念（a collection of data），并由此发展了“能解释地震记录的最优地下结构”的新范式（models that can best explain waveforms）.该方法同传统“单地震—单台站”接收函数相比，其核心思路为利用密集台阵的连续波场记录，从低信噪比数据中提取相干信号，更清晰有效地追踪地下结构.根据研究问题的尺度不同，该思路还可应用于刻画俯冲板片界面、岩石圈—软流圈界面（利用S波接收函数）、上地幔间断面等的研究中，通过基于密集台阵观测的地下精细结构建模，为定量地质解译提供可能.但台阵接收函数基于子台网下方界面连续平滑的假设，对于复杂地下结构，如断层等，台阵接收函数假设的合理性需根据台阵密度进行分析判断.后续需进一步针对复杂结构及台阵接收函数振幅信息开展更深入的研究，例如针对深大断裂进行超密集台阵接收函数分析、采用理论测试及长期台网观测来评估台阵概率性接收函数振幅信息的准确性等，更有效地将该方法拓展应用于接收函数反演和各向异性分析等.

2 接收函数界面成像研究进展

利用P波或/和S波接收函数资料，开展从地壳到下地幔顶部不同深度的界面成像，是接收函数研究的一项重要内容.基于研究对象和数据的空间覆盖情况，这方面的研究方法可分为单台分析和台阵成像两大类.

2.1 单台分析

单台分析法是基于单个地震台站提取的接收函数来约束台站下方的界面结构、界面至地表平均波速比（泊松比）、各向异性等信息的方法，具有直观、简单的特点.

2.1.1H-κ叠加

接收函数H-κ叠加方法（Zhu and Kanamori,2000）基于Moho面转换波和地表多次波与直达P波的到时关系来共同约束地壳厚度（H）与平均波速比（VP/VS,κ）信息.通常假设单个台站下方的地壳为单层水平均匀结构，来自Moho面的Ps和PpPs及PpSs+PsPs震相与直达P波的到时差分别是关于地壳厚度H、地壳平均P波速度VP0、地壳平均VP/VS以及射线参数的不同函数.给定VP0，对于单台接收的不同震中距（射线参数）的实际数据，搜索接收函数中三个震相按走时叠加能量最强的地壳厚度和平均VP/VS值，即获得同时满足三个函数关系的最佳地壳厚度与平均VP/VS.在结构简单的区域，Moho面转换波和多次波震相都比较清晰，且波形随反方位角变化较小，这种叠加方法能够有效约束台站之下的地壳厚度与平均VP/VS.但实际地壳往往不是简单的水平单层均匀结构.理论分析表明，当地壳存在厚的低速沉积层和复杂的壳幔过渡带（罗艳等，2008；危自根等，2016），或者倾斜界面（Lombardi et al.,2008;Wang et al.,2010）和各向异性结构（房立华和吴建平，2009；查小惠等，2013）等情况下，接收函数波形较为复杂，来自Moho面的转换和多次反射震相会受到其它信号干扰，从而导致接收函数H-κ叠加结果偏离真实值.针对这一问题，学者们进行了各种方法改进，以提高其适用性和结果精度.例如，利用4次方根H-κ叠加和深度域三种震相相关系数来减弱随机噪声影响的思路（Niu et al.,2007）；考虑Moho面倾斜情况的H-κ-θ方法（张洪双等，2009；谭萍，2018）；考虑Moho面倾斜和对称轴倾斜各向异性结构的Hκ-c方法（Li et al.,2019），以及采用不同策略分别获取沉积层和结晶地壳厚度与波速比信息的两层接收函数H-κ叠加方法（Yeck et al.,2013;Yu et al.,2015;Zhang and Huang,2019;Wei et al.,2020）等.

采用接收函数H-κ叠加及其改进方法获取地壳厚度和VP/VS（对应泊松比）分布，可为约束地壳岩石组分、应力状态和构造演化提供重要信息（Christensen,1996;Ji et al.,2009）.由于这种叠加方法能够避免人为拾取震相带来的不确定性，并易于快速、大批量分析数据，因此已被广泛用于全球大陆不同构造区域的地壳结构研究（如，He et al.,2014;Wang W et al.,2014;Wei et al.,2020）.然而，由于实际地壳结构的复杂性，接收函数H-κ叠加及其不同的改进方法均有各自的适用范围和结果的不确定性.对这类方法更有效的应用可能需要结合多频率分析和其它成像方法，多参数、多学科观测数据，以及理论模拟等手段开展综合研究（如，French et al.,2009;Yuan,2015;Wang et al.,2018;冯铭业等,2021）.

2.1.2 偏振分析

在单台接收函数分析中，既可基于接收函数Ps转换波及地表多次反射波的平均特征获得台站下方平均地壳结构信息，也可根据这些震相波形随反方位角的变化特征提取地壳结构的变化信息（例如，倾斜界面和/或各向异性结构）.非水平的速度界面（如倾斜结构）和介质性质的方向性（即各向异性）都会使切向接收函数产生能量，且与径向接收函数类似，表现出特定的随反方位角周期变化的偏振特性（Savage,1998;Frederiksen and Bostock,2000;Nagaya et al.,2008;房立华和吴建平,2009;Schulte-Pelkum and Mahan,2014;张建勇等,2019）.依据Ps转换震相的对称轴和极性转变位置可以获得台站下方界面倾向或各向异性快慢轴方向，进一步通过接收函数波形拟合可确定界面倾角、倾向与各向异性强度.相对于传统基于单个事件径向和切向接收函数Moho面Ps转换波分裂分析（与远震剪切波分裂分析类似）来提取地壳各向异性参数的方法，利用来自不同方位的单台接收函数集进行偏振分析的方法操作简便，结论直观、稳定，适用于地震事件方位覆盖较好的情况（如，Liu and Niu,2012）.该方法已广泛应用于单层或双层各向异性结构的理论分析和克拉通、陆内古老/活动构造带、俯冲带、碰撞带等不同构造区地壳至上地幔各向异性结构的实际研究中（如，Bostock,1997;Levin and Park,1997a;Frederiksen and Bostock,2000;Mercier et al.,2008;Nagaya et al.,2008;Bianchi et al.,2010;Sun et al.,2012;Schulte-Pelkum and Mahan,2014;Wirth and Long,2014;杨妍等,2018）.

然而，直接利用接收函数随反方位角的偏振特性提取倾斜界面与各向异性结构信息还面临许多困难.Frederiksen和Bostock（2000）通过理论测试总结了不同各向异性结构和倾斜结构对应的接收函数波形随反方位角的周期变化特性，发现对称轴倾斜各向异性与倾斜界面对接收函数的影响较为相近，难以有效区分.此外，倾斜结构或各向异性所产生的次级信号多湮没于反映界面速度跳变一阶结构的强信号中，加之噪声干扰（图4a、4c），限制了该方法的有效性和可行性.

为了更有效地开展单台接收函数集的偏振分析、提取倾斜界面或各向异性结构信息，近年来发展了多种新的分析方法.例如，近期发展的谐波分析方法（Park and Levin,2000），是基于各向异性结构、倾斜结构以及小尺度横向结构变化等引起接收函数波形随反方位角的变化具有不同谐波阶数的特征，来提取主体结构信息.通过对接收函数进行谐波分析和波形拟合，其最大振幅和能量对应的谐波阶数可用以判断倾斜和各向异性等结构的贡献（Bianchi et al.,2010;Sun et al.,2012;杨妍等,2018）.这一方法能够较大程度地减少倾斜结构与各向异性结构信号的相互干扰（王琼等，2016）.又如，将信号主成分分析方法引入到单台接收函数集处理中，通过选择不同主成分进行数据重构，来压制噪声、分离接收函数中反映结构一阶特征、倾斜或各向异性等结构变化特征的成分，实现同时提取结构共性和变化信息的目的（张建勇等，2019）.与直接采用不同反方位角的平均接收函数以及去除平均后的接收函数来反映结构共性和变化的方法（Schulte-Pelkum and Mahan,2014）相比，主成分分析方法不仅显著提高了接收函数数据的信噪比（图4a-4d），使更准确有效地分离结构主体特征与变化信息成为可能，而且给出了倾斜界面和各向异性共存情况下分离两种结构信息的初步参考（图4e、4f）.此外，该方法也提供了区分各向同性倾斜结构和对称轴倾斜各向异性结构贡献的新思路（图4g、4h）.在未来研究中，基于研究对象的结构特征选择合适的分析方法，或将不同分析方法结合、取长补短，可能是更充分、更准确地提取接收函数中结构信息的可行策略.

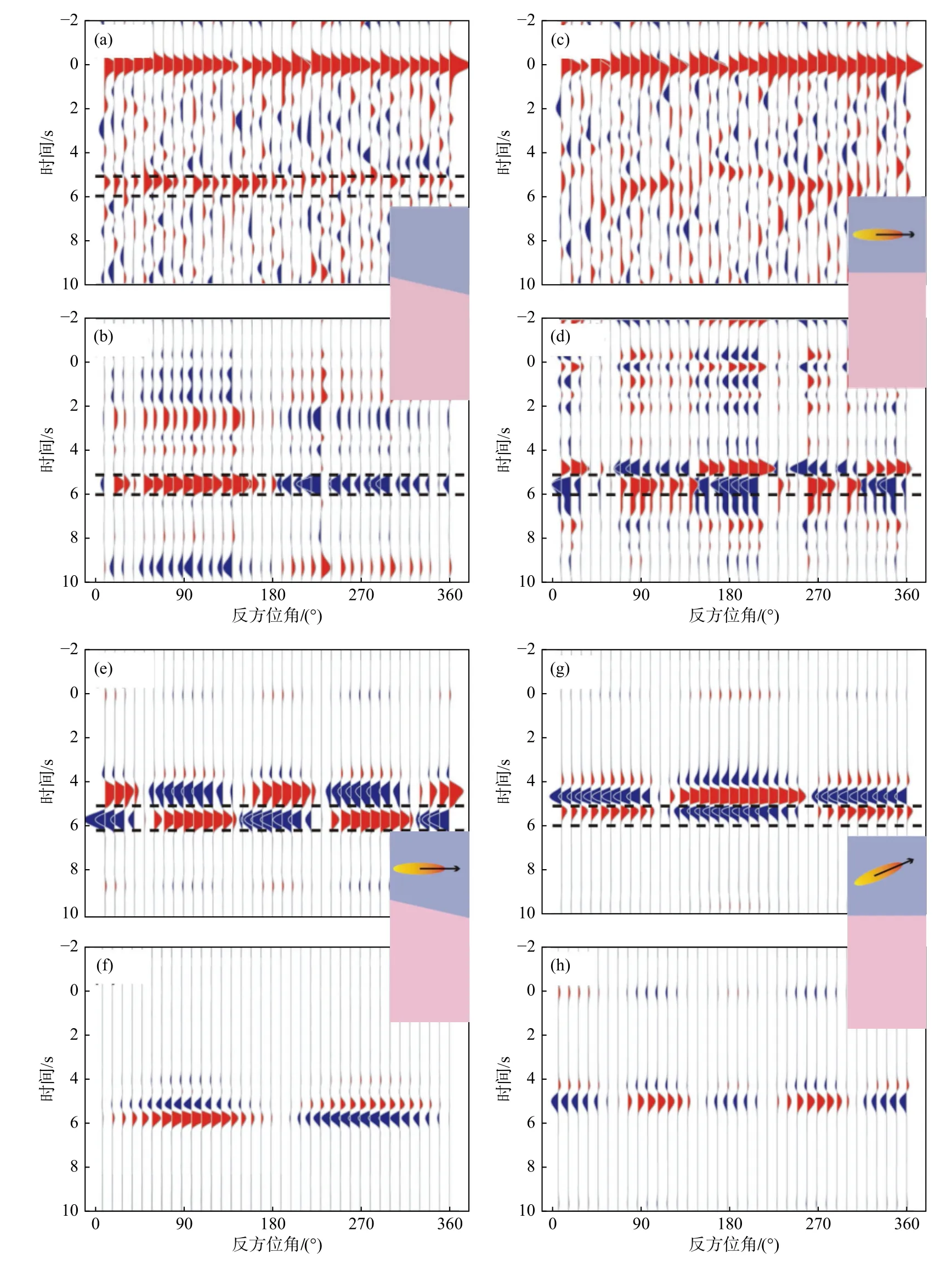
图4 理论径向接收函数及其主成分分析（修改自张建勇等，2019）.（a，b）分别为各向同性单一倾斜界面模型（加25%噪声）径向接收函数原始波形及第二主成分重构结果；（c，d）分别为对称轴水平各向异性模型（加25%噪声）径向接收函数原始波形及第二主成分重构结果.（e，f）分别为倾斜界面与对称轴水平各向异性共存、后者占主导的模型径向接收函第二、三主成分重构结果，振幅均放大5倍；（g，h）分别为对称轴倾斜各向异性模型径向接收函数第二、三主成分重构结果，振幅均放大5倍.图中红色表示正极性信号Fig.4 Principal component analysis of theoretical radial P-RFs (modified from Zhang et al.,2019).(a,b) Synthetic P-RF waveforms with 25% noise added and the reconstructions by the second principal component for an isotropic dipping discontinuity model;(c,d) Synthetic P-RF waveforms with 25% noise added and the reconstructions by the second principal component for an anisotropic model with a horizontal symmetry axis;(e,f) Reconstructed radial P-RFs by the second and third principal components,respectively,for a complex model with the coexistence of a dipping discontinuity and a dominant anisotropy structure with a horizontal symmetry axis (amplitudes are amplified by a factor of 5);(g,h) Reconstructed radial P-RFs by the second and the third principal components,respectively,for an anisotropic model with a dipping symmetry axis (amplitudes are amplified by a factor of 5).The waveforms with positive polarity are red-coded

2.2 台阵成像

随着地震台阵观测技术的发展和台站密度的增加，接收函数界面成像逐步实现了从基于单个台站数据向利用密集台阵数据的转变.借鉴勘探地震学中反射波资料分析处理思路，已发展了一系列基于台阵的接收函数叠加/偏移成像方法，并在地球内部结构探测中发挥着越来越重要的作用.接收函数台阵成像方法可分为基于高频射线近似的叠加方法和基于射线或波动理论的偏移成像两大类.

高频射线叠加方法是最早发展的台阵接收函数成像方法.Dueker和Sheehan（1997）首先将反射波共中心点（common mid-point,CMP）叠加的思想引入到接收函数转换波成像中，通过给定的速度模型将倾斜入射的接收函数按照理论走时与入射角关系进行动校正，并叠加获取台阵下方的界面起伏图像.随后，Zhu和Kanamori（2000）进一步改进该方法，提出了接收函数共转换点（common conversion point,CCP）叠加方法.根据给定的速度模型，CCP叠加方法将每条接收函数按射线路径反投影到空间域，并在空间域进行叠加成像（图5）.相对于CMP叠加方法每次只能针对某一深度聚焦，CCP叠加的优势在于同时对不同深度聚焦.CCP叠加方法使用简单，计算效率高，是目前地壳和上地幔界面结构研究中应用广泛的接收函数成像方法.但该方法基于水平层状介质假设，且仅考虑单一射线路径，对高倾角界面和结构存在强烈横向不均匀性的区域，如俯冲带、碰撞带等，由于无法处理绕射或散射波而难以获得真实结构图像（图6a、6c）.

近年来全球范围大规模密集地震台阵观测提供的优良数据空间覆盖以及计算能力的大幅提升，为将工业界普遍采用的高精度反射波偏移成像技术引入到接收函数分析处理中、获得地球内部界面的可靠图像提供了可能.偏移是将地表记录的地震波场延拓（偏移）至地下空间不同深度进行成像的过程.与将地表记录沿单一固定射线移动到地下空间进行CCP叠加的方法不同，偏移成像不再假设地下结构为水平层状介质，而是考虑更为普遍的地震散射波场（图5），从而可以有效消除绕射或散射造成的假象、实现存在强横向变化、高倾角界面等的复杂地下结构成像（图6b、6d）.相应地，偏移成像通常比CCP叠加计算成本高，特别是需要足够密集的台阵数据才能体现其成像优势（Shang et al.,2017）.这也是直到上世纪末、本世纪初全球密集台阵观测全面展开之后才提出接收函数偏移成像的原因.

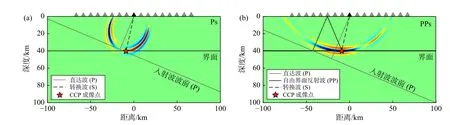
图5 接收函数共转换点叠加（CCP）成像（Zhu and Kanamori,2000）和体波散射核偏移成像（Hansen and Schmandt,2017）原理差异图.CCP叠加方法基于水平层状介质假设，将接收函数按固定射线路径（黑色虚线）反投影到空间域进行叠加成像（如红色五角星为成像点）；而散射波偏移成像则考虑地下可能的散射点（分布于图中彩色散射核区域），通过绕射波归位来获得高精度的地下结构成像.（a）Ps转换波散射核；（b）PpPs多次波散射核，其振幅反映对应散射点处的结构变化（修改自Hansen and Schmandt,2017）Fig.5 Diagrams showing the differences between common conversion point (CCP) stacking (Zhu and Kanamori,2000) and scattering kernel migration (Hansen and Schmandt,2017).The CCP stacking method is based on the assumption of horizontal layered media,in which the RFs are back-projected along the ray paths (black dashed line) and stacked at the conversion point(e.g.,the red star is the imaging point).Scattered wave migration,however,considers possible subsurface scattering points(distributed in the colored scattering kernel region),and can thus image subsurface structures with high precision.(a) Scattering kernels of Ps conversions;(b) Scattering kernels of multiples.The amplitudes reflect the structural changes at the corresponding scattering points required to match the observed scattered phases (modified from Hansen and Schmandt,2017)

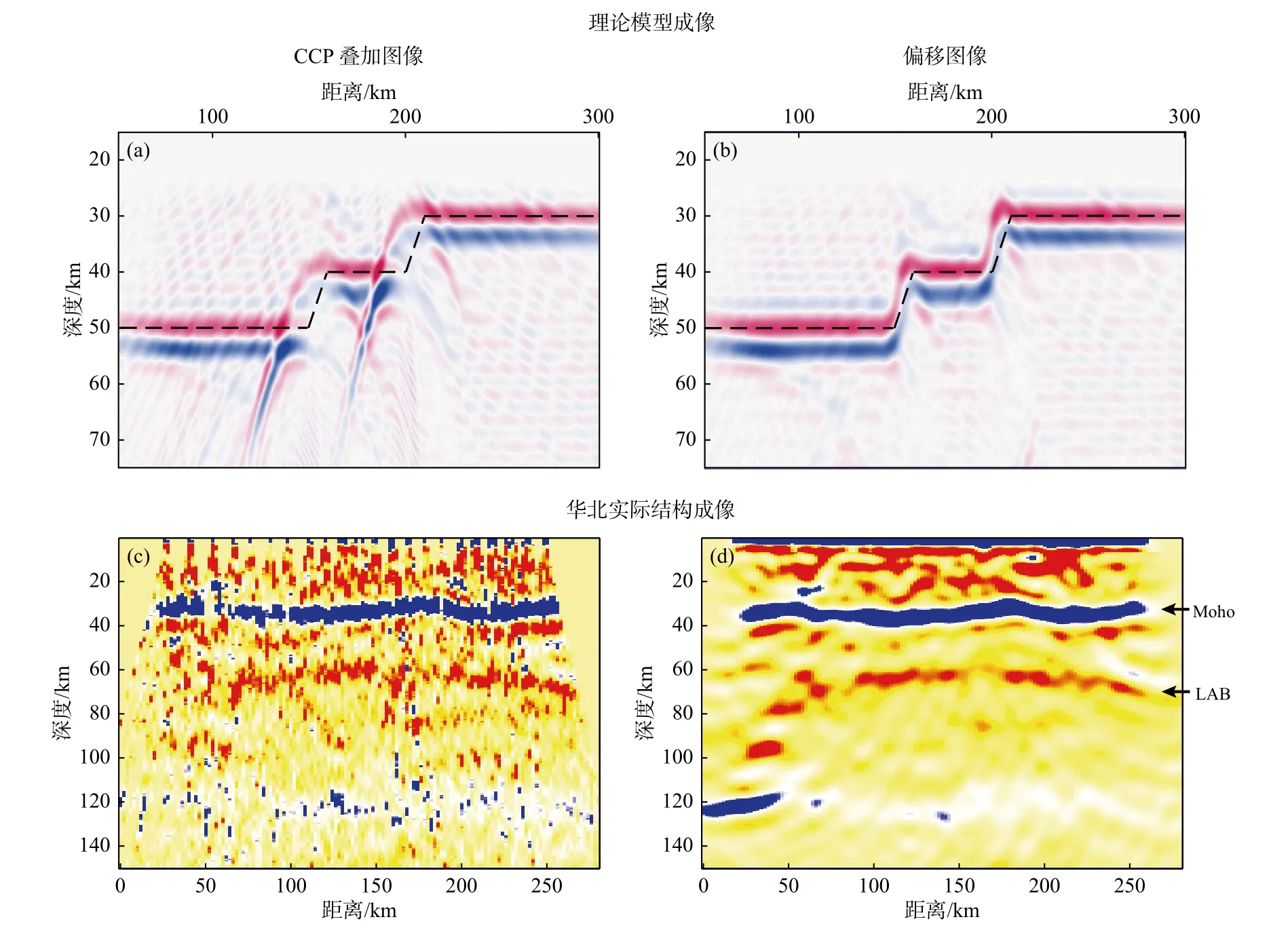
图6 接收函数CCP叠加成像（a，c）与偏移成像（b，d）结果对比.（a，b）为理论模型成像结果（修改自Abe and Brown,2002），其中黑色虚线代表理论模型界面;（c，d）为华北东部剖面结构图像（修改自Chen et al.,2006a），其中～30 km深度处的蓝色信号为Moho面，～60～80 km处的红色信号为LAB.（b，d）分别为Kirchhoff叠前偏移和波动方程叠后偏移图像.与不考虑散射和绕射的CCP叠加图像（a，c）相比，偏移图像（b，d）具有更高的信噪比，更有效恢复结构的横向变化特征Fig.6 Comparison of P-RF CCP stacking (a,c) and migration (b,d) images.(a,b) P-RF imaging results for a theoretical stair-step model,where the black dashed lines represent the locations of input seismic discontinuities (modified from Abe and Brown,2002);(c,d) P-RF images along a profile across the eastern part of North China (modified from Chen et al.,2006a),where the blue signal at～30 km depth marks the Moho discontinuity and the red one at～60～80 km represents the LAB.(b,d) are obtained from Kirchhoff pre-stack migration and wave equation post-stacking migration,respectively.Compared with CCP stacking images (a,c) without considering scattering and diffraction,the migrated images (b,d) exhibit higher signal-to-noise ratios and thus can more effectively recover the lateral structural variations

借鉴工业界反射波偏移的思想，过去20多年已发展了一系列接收函数偏移成像方法.例如，基于Kirchhoff高频射线近似思想的接收函数偏移方法（Ryberg and Weber,2000;Sheehan et al.,2000;Levander et al.,2005;吴庆举等,2007b;Cheng et al.,2016;Millet et al.,2019），以及采用不同波场分解和偏移技术的改进方法，如基于τ-p变换的平面波偏移方法（Poppeliers and Pavlis,2003a,2003b），基于反向散射理论的广义Radon变换偏移方法（Bostock and Rondenay,1999;Bostock et al.,2001;Liu and Levander,2013），基于有限频体波散射核理论的三维叠前偏移方法（Hansen and Schmandt,2017;Zhang and Schmandt,2019）等.与上述射线类方法不同，另一类接收函数偏移成像方法是从波动理论出发而提出的，包括基于波动方程的接收函数叠后偏移（Pavlis,2003;Chen et al.,2005a,2005b）和叠前偏移方法（Shang et al.,2012;Li et al.,2018;Jiang et al.,2019）等.这些方法除了叠后与叠前之分外，主要不同之处在于采用的波场延拓算子以及2D与3D成像的区别，如Chen等（2005a,2005b）采用2D相位屏深度偏移，Shang等（2012）、Li 等（2018）分别采用2D和3D有限差分逆时偏移，而Jiang等（2019）采用3D相移+插值逆时偏移.

射线类和波动方程类接收函数偏移方法具有不同的特点和适用范围.通常而言，射线类偏移成像方法计算快速灵活、效率相对较高，能够恢复平缓变化的界面结构；但对于复杂结构中多射线路径、影区以及混乱射线等情况，存在固有困难和问题，难以精确成像.而波动方程偏移方法考虑地震波场的物理波动本质，能够更准确地恢复复杂介质中的波场传播特征、更有效压制噪声，从而克服了射线方法的上述困难，提高了复杂结构的成像质量（Chen et al.,2005a）.然而，波动方程偏移往往计算量大、计算效率低，而且需要相对更为密集、均匀的数据空间覆盖，因此其3D方法的发展及应用仍十分有限（Li et al.,2018）.需要说明的是，在波动方程偏移框架下，2D偏移方法理论上可以通过将2D波场延拓算子替换为相应的3D算子而直接拓展为3D偏移，但在技术上需要克服计算量和存储空间剧增带来的困难.为了兼顾计算效率和成像精度，近年来有学者将有限频地震波走时计算的思路（如，Dahlen et al.,2000）引入到射线偏移中，提出了接收函数有限频散射核3D偏移方法（Hansen and Schmandt,2017;Zhang and Schmandt,2019）.这种接收函数偏移成像方法介于射线类和波动方程类之间、应用相对灵活，但其本质仍属于射线类方法.

总体而言，接收函数偏移成像方法经历了从叠后偏移到叠前偏移、从二维偏移到三维偏移、从射线到有限频乃至波动成像的发展.随着全球范围宽频带和短周期密集地震台阵观测的大规模开展，接收函数偏移成像方法已成功应用于地壳（Wang et al.,2018;Jiang et al.,2019）、岩石圈—软流圈（Chen et al.,2005b,2014;Shang et al.,2017;Wu et al.,2021）、地幔过渡带甚至下地幔顶部（Chen et al.,2009;Zhang and Schmandt,2019）不同深度和横向范围的实际界面结构研究中.尽管偏移成像在压制噪声、提高分辨率、恢复复杂结构特征等方面比常规CCP叠加成像表现出明显的优越性（图6），但这并不意味着要抛弃CCP叠加成像以及单台分析方法.在更多情况下，需要根据实际地震观测资料质量、空间覆盖情况以及研究目标，选取合适的成像算法.如针对覆盖稀疏的地震资料，CCP叠加成像、甚至单台分析方法往往可以快速、有效地获得地下界面结构信息；若有密集台阵观测资料，特别是研究目标包括倾斜界面、复杂构造等，可根据资料的覆盖程度和/或结构的复杂程度选取射线或波动方程偏移成像算法，以最大程度地利用资料、发挥方法的优势.

2.3 问题与解决思路

新观测、新方法、新技术，始终是驱动地球内部精细结构成像的原创动力.从观测角度，需要进一步发展和规范地震台阵观测技术，积累高密集空间采样、高质量、长期的地震观测资料.此外，实际台站布设往往是不等间距的，而高精度的偏移成像需要等间距的观测资料.因此，在积极开展密集台阵观测的基础上，还需要发展相应的地震数据正则化方法，以便更好地服务地震偏移成像（如，Shang et al.,2017;Zhang et al.,2022）.从方法技术角度，目前多数接收函数界面成像的主要目标是界面深度及其横向变化，而对界面厚度、P波和S波速度变化、密度变化等结构参数研究较少，因而无法全面约束目标界面的结构和性质.由于不同反射波、转换波对各界面结构参数的敏感度不同，并依赖于频率/波长（详见4.1，Bostock,1999;Julià,2007），因此完整的界面结构成像需要多类型、多频率震相联合约束.目前虽然在接收函数多震相联合（Ps与Sp、Ps与多次波）成像方面已经开展了众多方法和应用研究（如，Bostock et al.,2001;Chen et al.,2006b;Zheng et al.,2006;Julià,2007;Rychert et al.,2007;Chen,2009;Abt et al.,2010;Millet et al.,2019;Zhang et al.,2019;He et al.,2022），但接收函数与其它散射波联合成像的研究有限（如，Lawrence and Shearer,2006），对界面不同结构参数的定量约束更少.因此仍需要新的成像思路，并进一步开展新的和已有成像方法的有效性验证及其实际应用研究.将接收函数中的转换波、多次波信号与利用地震尾波或背景噪声干涉提取的界面反射波信号联合，共同约束目标界面结构，近年来已成为提高界面成像有效性的一个新思路（Wang et al.,2020;Feng et al.,2022）.此外，与勘探地震学中的反射波成像类似，接收函数叠加/偏移成像的精度、准确性还取决于接收函数本身的质量、背景速度模型的准确性等.为此，未来研究需进一步优化接收函数提取方法，特别是针对目前快速发展的短周期密集台阵探测中波形噪声水平高、观测周期短等问题，发展相应的接收函数反褶积算法，提升反褶积的稳定性（Zhong and Zhan,2020;Wang et al.,2021a）；同时发展接收函数波速成像方法，并协同体波、面波、噪声、全波形等地震层析成像方法，提升速度模型的准确性，以便更有效地开展接收函数界面精细结构成像.

3 接收函数波速成像研究进展

接收函数中包含的直达波和壳幔界面初次转换波和多次反射波震相的走时和振幅分别受界面深度及其之上平均速度、界面处S波速度和密度变化的控制（Zhu and Kanamori,2000;Julià,2007）.直达波振幅主要与浅表的速度结构有关，转换波振幅主要对S波速度变化敏感，而多次反射波对S波速度和密度变化均敏感（Julià,2007）.由于不同频率地震波在空间敏感度上的差异，接收函数波形也随频率改变而发生变化（Bostock,1999;van der Meijde et al.,2003;王旭等,2019）.整体而言，低频数据对大尺度结构变化敏感，高频数据对小尺度结构变化更敏感.因此，利用接收函数波形及其频率变化特征可以反演地壳和上地幔介质速度结构变化.

3.1 接收函数波形反演

随着密集台阵观测技术以及计算能力的不断发展，接收函数波形反演经历了从线性向非线性、从单一数据向多数据联合的演变.得益于不断提高的计算效率，通过有限差分格式数值计算偏导数矩阵的接收函数迭代线性反演技术率先得到发展和应用（Owens et al.,1984,1987;Ammon et al.,1990）.然而，基于偏导数矩阵的线性反演过程容易陷入局部极小，导致对初始模型过度依赖.界面深度与绝对速度的折中效应使这一问题在接收函数波形反演中更加凸显（Ammon et al.,1990）.为此，全局优化的接收函数非线性反演方法得到快速发展，如遗传算法（Shibutani et al.,1996；Levin and Park,1997b;吴建平等,2001）、快速模拟退火法（Zhao et al.,1996）、邻域算法（Sambridge,1999a,1999b）和模拟退火法（Vinnik et al.,2004,2006;Zheng et al.,2005）等.这些方法能够实现大模型空间的有效搜索，避免陷入局部最小，在无需线性化或偏导计算情况下提供最优模型（簇）.

接收函数与其他独立观测资料的联合反演使接收函数波形反演方法迈入成熟阶段.地球物理反问题的本质决定了任何单一观测均对应由一系列模型构成的解空间.因此，联合多种独立观测资料是减小解空间范围的有效途径.面波观测与接收函数具有相似之处，即两者均对S波速度敏感，不同的是前者对绝对速度敏感而后者对速度强烈变化（界面）敏感（图7a-7d）.两者的联合能够同时对绝对速度和界面结构进行有效约束，同时减小反演的非唯一性.因此在过去的近30年里，接收函数与面波频散的联合反演成为岩石圈速度结构研究的最流行方法之一（如，Wang C Y et al.,2014;Cai et al.,2021）.尤其是，地震环境噪声研究在提取短周期面波频散上取得的突破性进展（Shapiro and Campillo,2004），使接收函数与面波频散的联合反演在地壳速度结构研究中得到了广泛应用（如，Liu et al.,2014）.接收函数与面波频散联合反演也经历了从线性反演（Özalaybey et al.,1997;Julià et al.,2000）向非线性反演的演变，如遗传算法（Chang et al.,2004）、生态位遗传算法（Lawrence and Wiens,2004）和贝叶斯蒙特卡罗方法（刘启元等,2010;Shen et al.,2013）等.非线性反演虽然有效降低了反演对初始模型的依赖，但不同数据权重和模型参数化问题一直存在争议.Bodin等（2012）发展了接收函数与面波频散联合的跨维度反演技术（transdimentional inversion;图7）.该方法将模型维度与噪声水平均作为变量进行统计分析（图7g-7i），这不仅较大程度上降低了模型自由度，而且实现了非人为主观控制的数据加权.随着人们对地震数据挖掘的不断深入，更多不同类型数据联合反演也在不断推进，如接收函数、面波频散与面波椭圆率的联合反演（Zhang and Yao,2017;Wang et al.,2019），接收函数、P波极化与面波椭圆率联合反演（Xiao et al.,2021），接收函数与重力资料联合反演（Shi et al.,2018）等.

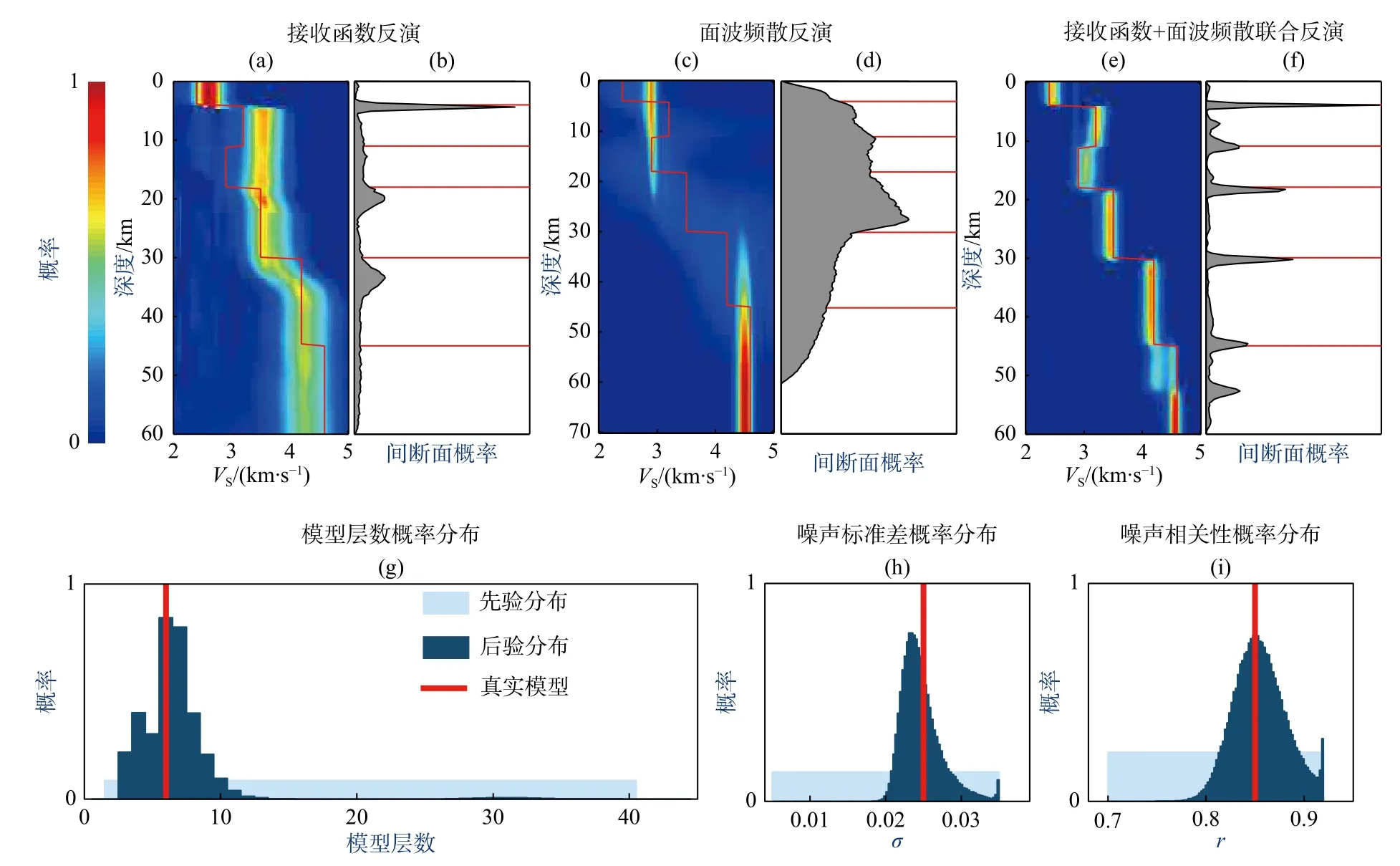
图7 贝叶斯跨维度联合反演示例（a-f）以及模型层数（g）和噪声水平概率分布（h，i）（修改自Bodin et al.,2012）.图（a，c，e）中红线为真实模型，背景为后验模型概率分布.图（b，d，f）为不同深度界面的后验概率分布.图（g，h，i）中浅蓝色、深蓝色区域和红线分别代表均匀先验分布、后验分布和真实模型Fig.7 Examples of Bayesian transdimentional inversion (a-f) and the probability distributions of layer number (g) and noise level (h,i) (modified from Bodin et al.,2012).The red line in (a,c,e) marks the input model,and the background shows the posterior probability distribution for the inverted models.(b,d,f) are posterior probability distributions for the presence of discontinuities at depth.The light blue and dark blue histograms and the red lines in (g,h,i) represent the uniform prior distribution,the posterior distribution,and the true model,respectively

相比于面波数据，接收函数明显优势是对台站下方结构的小孔径采样，因此具有较高的横向分辨率.两者联合更多受控于面波强烈的横向平均效应，牺牲了接收函数的横向分辨率.因此，在不引入其他独立观测的前提下减小反演非唯一性成为发挥接收函数横向分辨率优势的关键.多频率接收函数反演（Wu et al.,2007;Bissig et al.,2021）、P波与S波接收函数联合反演（Vinnik et al.,2004;Bissig et al.,2021）、接收函数波形反演与CCP成像联合（Zheng et al.,2006）、基于二维密集台阵的接收函数走时反演（Jiang et al.,2021）和共转换振幅反演（Zheng et al.,2022）等方法均取得了不错效果.但是，这些方法并未从根本上克服接收函数波形反演的多解性和不稳定问题，即小量的速度改变会引起接收函数波形的巨大差异.因此，如何更有效地利用接收函数约束台站下方的波速结构仍需要新的思路.

3.2 体波振幅比反演

地震体波振幅比，即体波垂直分量与水平分量的振幅比值，是一种主要对台站下方速度结构敏感的单台测量参数（Wiechert,1907;Nuttli and Whitmore,1961;Aki and Richards,2002;Ni et al.,2014）.由于震源函数固有的复杂性以及噪声影响，从原始地震波形记录中直接提取体波振幅比非常困难，导致相关研究一直比较有限（Krüger,1994）.Svenningsen和Jacobsen（2007）首次提出利用P波径向和垂向接收函数分别替代原始地震P波径向和垂向分量来估计P波振幅比（亦称之为P波径向和垂向接收函数振幅比）的思路，随后该思路在海底和陆地观测中均得到快速发展与应用（Kieling,2011;彭恒初等,2012;Hannemann et al.,2016;Lan et al.,2022;Yao et al.,2022）.由于P波径向和垂向接收函数振幅比对绝对速度更敏感，它与接收函数波形的联合反演不仅有效减小了解的非唯一性，而且保留了接收函数本身的横向高分辨率优势（Chong et al.,2018）.

近些年来，体波振幅比在约束浅部地壳速度结构的能力逐渐受到关注.理论研究表明，P波水平—垂直振幅比主要对近地表S波速度结构敏感，而S波垂直—水平振幅比对近地表S波速度和P波速度均敏感（Aki and Richards,2002）.Park和Ishii（2018）利用主成分分析方法提取了P波和S波振幅比，并对浅表S波和P波速度结构进行了联合约束.然而这项研究并未对获得的波速结构的深度范围进行深入探讨.Park等（2019）进一步分析了P波水平—垂直振幅比的频率依赖性，并利用这种性质定性约束了浅部S波速度结构随深度的变化；但该研究并未关注P波速度结构，因而缺乏对泊松比的约束.理论推导与数值实验表明，接收函数直达波振幅本质上代表了体波振幅比，能够有效约束浅部速度结构（Julià,2007;钱银苹等,2018;王旭等,2019）.在此基础上，Wang等（2021b）发展了基于远震体波振幅比的浅部地壳波速和泊松比结构成像方法（图8）.该方法首先通过提取接收函数剔除震源函数、路径信息以及仪器响应的影响，并计算不同频率范围的P波水平—垂直振幅比和S波垂直—水平振幅比；再通过高效算法反演获取地震波速与泊松比结构.相比于传统的体波走时或面波成像技术，该方法具有以下几点优势：（1）体波频率成分明显高于面波，因此具有更高的垂向分辨率；（2）适用于单个台站，横向分辨率主要依赖于台站间距；（3）利用远震接收函数特点，不受震源、路径影响，而且适用于构造不活跃地区.该研究旨在建立近地表精细地震勘探和深部大尺度被动源成像之间的联系桥梁，进而将实验室测量、浅表地质结构勘查与深部地球物理探测有机结合，以全面理解地球内部尤其是地壳的结构、性质与变形机制.另外，因为不需要先验震源函数信息和稠密射线路径覆盖，该研究为现今全球丰富的宽频带地震观测资料的深度使用以及全球范围浅部结构的精细成像提供了重要的方法基础.

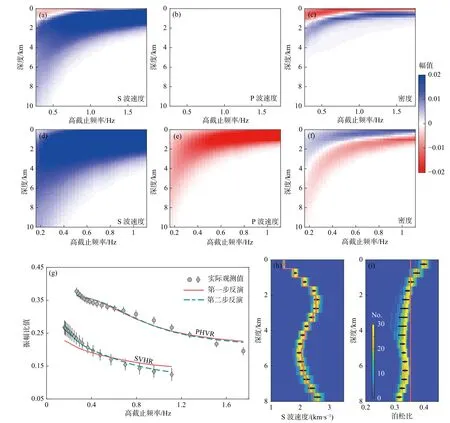
图8 随频率变化的P波水平—垂直振幅比（PHVR,a-c）和S波垂直—水平振幅比（SVHR,d-f）对S波速度、P波速度和密度的深度敏感核，体波振幅比（g）与反演速度结构（h-i）示例（修改自Wang et al.,2021b）.图（g）中，浅红线和深绿线分别代表了第一步反演和第二步反演500个最优模型平均结果对应的预测；图（h，i）中浅红线代表了第一步反演结果，背景色代表了第二步反演500个最优模型的概率分布Fig.8 Frequency-dependent sensitivity kernels of P-wave horizontal-vertical amplitude ratio (PHVR,a-c) and S-wave vertical-horizontal amplitude ratio (SVHR,d-f) to S-wave velocity,P-wave velocity and density,and an example showing the body-wave amplitude ratios (g) and inverted structures (h-i) (modified from Wang et al.,2021b).In (g),the light red and dark green lines represent the predictions by the average of the 500 best-fit models from the first-step and second-step inversions,respectively;the light red line in (h,i) represents the results after the first-step inversion,and the background color represents the probability distribution of the 500 best-fit models after the second-step inversion

3.3 问题与解决思路

接收函数波形或振幅比反演结果的准确性主要取决于接收函数数据的可靠性和准确性、正演与反演技术的有效性.自接收函数方法提出以来，其提取技术得到了不断提升与发展，从频率域到时间域，从线性到非线性，从单台站—单事件到基于台阵的事件簇（见2.2节和2.3节）.但是，如何提高接收函数波形尤其是振幅的准确性仍是相关研究的前沿与难点.噪声干扰是影响接收函数提取的主要因素，因此发展有效的去噪技术是解决该问题的有效途径.

尽管基于接收函数反演地震波速以及将接收函数与其他观测数据联合反演的方法已得到长足发展，但是这些方法至今仍以一维反演为主，即假设地下结构为均匀水平层状介质，忽略结构的各向异性和横向不均一性.利用接收函数约束介质各向异性的现有研究主要基于对界面转换波震相极性和走时的反方位分析（见3.1.2节），而基于全局优化的反演算法仍处于起步阶段（田宝峰等，2008）.针对倾斜界面结构和各向异性介质进一步发展高效正演模拟算法是推进反演算法的关键.此外，起伏地表引起的散射波场也会对接收函数产生直接影响（Monteiller et al.,2013;García-Pérez et al.,2021）.随着台阵观测的不断加密以及超级计算机的迅速发展，发展起伏地表条件下的二维和三维正演模拟技术是实现接收函数波速结构准确成像的基础，将研究区视为一个整体实现二维甚至三维结构反演是其未来长期的发展目标.

接收函数波速成像的有效范围主要集中在地壳或岩石圈尺度（100 km以浅），而对更深部地幔波速结构的约束能力较弱.原因主要包括以下两点：（1）深部界面转换波和多次波信号能量弱且易受其它震相和噪声干扰；（2）随着深度增加，来自不同震中距或反方位接收函数的空间覆盖范围显著增大，结构的横向不均一性会降低接收函数叠加的有效性，限制深部信号信噪比的提高.因此，开展深部（＞100 km）地幔接收函数波速成像研究可能需要从以下几点着手：（1）发展有效的假象剔除和去噪技术，并采用合理的时间域CCP叠加替代单台接收函数叠加，以提高深部结构信号的信噪比；（2）利用先验结构信息，集中针对特定深度范围目标结构，先低频、后高频分频率迭代反演，兼顾结构横向不均一性和空间分辨率；（3）结合对目标深度结构敏感的其它观测数据，如长周期面波、体波反射信号等，开展联合约束成像.

4 未来发展方向

随着地震观测技术和探测能力的迅速发展，详细探测地球与行星内部不同尺度和空间范围的结构和物性状态，是当前地震学发展的趋势.近年来，地震观测系统正快速经历从“稀疏台站”到“密集台阵”的转变，如重点区域固定台网的建设或加密，宽频带密集流动地震台阵、短周期超密集流动地震台阵等在全球大规模的开展.海量地震数据的获得给接收函数研究提供了更多的机遇，同时也提出了更大的挑战：如何基于海量密集台阵资料，更充分有效地提取地下结构信息？

从人工资料处理走向人工智能分析：海量地震资料的不断积累，已无法通过人工处理方式高效地从地震记录中及时获取高质量的接收函数数据.因此，亟需发展基于人工智能提取和挑选接收函数的算法，对海量地震资料进行快速、高精度的自动分析、计算和筛选；并通过人工智能，在挑选出的大量接收函数数据中尝试识别和提取传统地球物理数据分析方法不易发现的“异常”特征和规律，助力地球内部界面和波速结构研究.

从“低频”走向“高频”、“多频”：实际地球中的界面结构复杂多样，既有化学成分跳变造成的尖锐间断面，又有由于矿物相变具有一定的温压范围、物质能量交换普遍发生等产生的一定厚度的过渡带结构.这就要求利用不同频率成分、能够探测不同厚度界面结构的接收函数开展分析研究.特别是，现今的接收函数研究不仅局限于壳幔尺度结构探测，而且已开始向浅层高精度成像迈进（如，Jiang et al.,2021;Wang et al.,2021a,2021b;Lan et al.,2022）.其关键在于如何扩展接收函数本身的频率组成，尤其是高频成分，从而拓宽其有效结构探测范围、提高空间分辨率.因此，接收函数研究必将越来越重视多频率分析与成像.其中，基于短周期密集观测（提高观测频率）和高频近震事件（采用高频数据），发展新的高频反褶积技术是未来接收函数小尺度精细成像的重要突破方向.

突破观测系统限制，从“遥感”走向“近测”：接收函数方法的探测优势是地震台站/台阵下方的壳幔界面和波速结构，因此其探测的有效性依赖于地表地震观测系统.现有地震台站分布的不均匀制约了接收函数方法对壳幔结构的探测范围、成像精度和分辨率.突破这种观测系统的限制、开展方法创新，应是未来壳幔结构研究的一项重要内容.近年来利用地震波场干涉思想和技术，从连续噪声记录或地震尾波中提取结构信号、特别是成功提取壳幔界面的反射体波信号（如，Zhan et al.,2010;Poli et al.,2012;Wang et al.,2015;Tkalčić et al.,2020;Feng et al.,2022），有望极大地补充和拓展现有观测系统对壳幔界面的采样范围、补充接收函数转换波对界面的约束.此外，通过波场干涉或延拓，将地表观测系统“移动”到接近深部界面研究目标，使“遥感”变为“近测”（如，source-receiver redatuming,Poliannikov et al.,2012;Shen and Zhan,2020），有望提高深部界面及相应波速结构成像的精度和分辨率.将这些思路和方法有效应用于实际结构探测，尚有待于在地震学干涉理论、信号提取和分析技术，以及转换波与反射波综合成像方法等方面取得突破.