浅地表面波成像技术研究进展与展望
2022-07-12汪利民夏江海罗银河卞爱飞
汪利民,夏江海,罗银河,卞爱飞
1 中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室,武汉 430074
2 浙江大学地球科学学院 浙江省地学大数据与地球深部资源重点实验室,杭州 310027
0 引言
地球浅地表,与人类生存和生活息息相关的一个圈层,支撑着人类生存与发展所需的一切.随着文明的发展,人类对从地球浅表圈层所攫取的包括油气、矿产、水等在内的自然资源的需求与日俱增.人类也早已意识到,当人们不断从地球浅表圈层攫取资源时,也需要与浅地表和谐共存.近二十年是中国经济高速发展的二十年,也是中国城市化进程最快速的时代,城市地下大约200 m厚度的地层物质及结构以不同的形式改变了其原有面貌.我们需要采用必要的地球物理手段,实时并精确地把握住这些变化方方面面的细节,以确保地下和地面建筑设施的稳固、清洁水资源的获取等.在基础工程和土壤机理研究中,指示土层或岩层软硬程度的指标性参数为N值.N值的大小与地下介质的横波速度大小具有直接的相关性(Imai and Tonouchi,1982).这使得介质中的横波速度参数成为浅地表物质最为关键的地震学物性参数之一.同时,横波速度也是评估浅层地质界面动力学特征和地震区划依据的重要参数(Yilmaz et al.,2006).建筑工程上,人们也通常利用地表以下30 m以内介质的平均横波速度参数作为依据,对场地土进行分类,满足地震工程不同类型的设计需求,如美国制定的UBC通用建筑准则(Uniform Building Code)以及欧盟制定的类似规范EC8(Eurocode8).另外,浅地表横波速度参数也是油气资源勘查中用以消除浅地表疏松介质对深地层反射信息模糊效应的重要参数.为获得浅地表介质横波速度参数,过去的常用方法为横波(SH波)折射法,这是环境与工程地球物理勘查中的常用方法之一,但该方法仅在横向均匀且速度递增的简单水平层状地层模型中适用.若地层界面倾斜或存在低速夹层时,得到的横波速度剖面分辨率低甚至完全不准确(Xia et al.,2002a),无法满足前述对浅地表介质精细刻画的需求.
通过反演地震信号中的面波成分构建地球壳幔尺度横波速度结构的方法最早在1960年代即被提出(Dorman and Ewing,1962),且已有非常系统的研究(Aki and Richard,1980).这样的方法技术在1980年代开始逐渐从全球壳幔尺度或区域尺度发展至浅地表小尺度工程与环境地球物理勘查中(Song et al.,1989).面波特指沿着某一特定介质分界面(如自由地表)附近传播,其能量主要集中在一个波长内的一类特殊的地震波.它们是地震波中的体波成分在自由表面或岩层介质分界面上相互干涉而形成的一类特殊波动.浅地表地震勘探利用的面波信号主要包括瑞利波(Rayleigh wave)和勒夫波(Love wave)两种.瑞利波由纵波与横波中的SV波在自由地表附近的相长干涉而产生.1885年英国物理学家瑞利(Lord Rayleigh)在研究均匀半空间介质中弹性波传播性质时预言了其存在(Rayleigh,1885).勒夫波于1911年由Augustus Edward Hough Love最先在数学上预测了其存在,并以其名字Love命名(Love,1911).它由横波中的SH波及其在地层间的反射、多次反射、折射等在地表的干涉和叠加形成,存在条件与SH型折射波一致(Luo et al.,2010).由于勒夫波的激发与存在条件较为苛刻,其观测难度相对于瑞利波而言要难得多,因此早期的面波勘探研究主要针对的是瑞利波,而勒夫波的研究则多体现在天然地震研究中.国内利用勒夫波和瑞利波群速度频散特性研究我国大陆地壳厚度的成果最早见于1960年代(宋仲和和谭承业,1965).陈运泰(1974a,1974b)推导出了层状各向同性弹性介质中的勒夫波频散方程和点源辐射条件下的勒夫波位移谱表达式,并解释了各参数项的物理意义,提出勒夫波可用于震源机制、震源深度位置确定和地壳及上地幔结构研究.后来石耀霖和金文(1995)对青藏高原获得的勒夫波群速度频散曲线,采用遗传算法进行反演,得到了该区地壳厚度及岩石圈横波速度结构,发现在25~35 km存在横波速度为2.7 km/s的低速层.
在天然地震中,一般而言,瑞利波是破坏性最强的一种地震波.在以反射波和折射波方法为主的油气地震勘探以及浅层人工地震勘探领域,瑞利波是能量最强的一种干扰波.关于瑞利波的研究,早期主要是根据其传播特性,设计合理的抗震结构或观测方式来减小它的危害或消除它对勘探地震资料成果的干扰.但自从面波在层状介质中的频散性质被发现后,又由于其传播时横向上振幅衰减小、信噪比高等特点,逐渐被当作有效波广泛应用在区域和全球尺度地震学领域进行地球内部结构成像(何正勤等,2007;张智等,2008;曾求等,2020)、浅地表地球物理工程领域开展精细地质调查(刘强,2009;Eker et al.,2012;夏江海等,2015)、超声无损检测领域开展精细结构检测与监测工作(Cho,2003)、油气勘探中复杂浅地表条件的静校正问题(Yang et al.,2011)等.
利用面波进行浅地表横波速度结构成像应用研究上,Nazarian 等(1983)在测试公路厚度与弹性模量时提出了表面波谱分析方法SASW(Spectral Analysis of Surface Waves).但使用该方法时,有效波难以从干扰波中分离,且面波频散曲线提取精度较差.为克服这些缺点,美国堪萨斯地质调查局KGS(Kansas Geological Survey,University of Kansas)对瑞利波勘探技术进行深入研究后,提出了面波多道分析法(Multichannel Analysis of Surface Waves,MASW)(Park et al.,1999;Xia et al.,1999),充分利用近十几年来的信号处理技术,大大提高了面波的勘探能力.多道面波分析方法自问世后便在环境与工程地球物理界受到了广泛的关注,被认为是获取浅地表横波速度参数的最优方法.该方法的思想源于堪萨斯地质调查所Song等(1989)从规则线型多道排列采集的浅震单炮记录中提取面波频散信息估计浅地表横波速度的一次尝试,之后演变发展至今成为浅地表地球物理勘探的重要方法之一.多道面波分析方法利用锤击方式激发瞬态面波信号,采用多道垂直分量检波器等间距的方式采集多道面波信号.通过一定的数学手段,将所采集的时空域内的多道面波信号转换到频率—速度域中,获得面波频散曲线后反演得到测线下方的横波速度结构(Park et al.,1999;Xia et al.,1999)
多道面波分析方法数据处理过程较为简单,处理步骤中最为关键的一步是多道面波信号的频散能量图生成过程.这一过程常采用的数学方法有τ-p变换、f-k变换、相移法(Park et al.,1998)、倾斜叠加法(Xia et al.,2007)、高分辨率拉东变换法(Luo et al.,2008)、频率—贝塞尔变换法(Wang et al.,2019;杨振涛等,2019)等.因此,该方法可以说是目前浅地表横波速度结构成像研究中最为便捷实用的方法.研究表明该方法获得的横波速度结果可靠,对比通过测井手段获得的横波速度,其差异在15%以内(Xia et al.,2002b),且甚至可得到相比于测井记录更可靠的浅地表1~2 m深度内的横波速度,而这仅是通过反演基阶模式面波的结果.多模频散曲线联合反演方法则可极大提高横波速度结果的精度,且反演过程更稳定(Xia et al.,2000,2003;Beaty et al.,2002;鲁来玉等,2006;凡友华等,2007;Lu et al.,2007;Luo et al.,2007;Song et al.,2007).Park等(2006)讨论了联合使用主动源和被动源的优点和问题,将多道面波分析方法应用范围拓展为主动源和被动源法,利用被动源法提高面波低频段频散数据精度,利用主动源法提高面波勘探高频段频散数据精度,进一步丰富和完善了多道面波分析方法的技术内涵,提高了面波浅层勘探的能力.相比于在勘探场地通过地质钻孔,用传感器在不同深度接收地面激发的横波得到横波速度深度剖面的直接测量法而言,多道面波分析方法具有高效率、低成本、无损、非侵入等明显优势,在城市地下结构精细探测工作中,具有广阔的应用范围和巨大的发展潜力(夏江海等,2015).目前已成为浅地表横波速度成像的主要方法,被成功用于解决一系列的浅地表地球物理和地质问题(杨成林,1993;Miller et al.,1999;Ivanov et al.,2006;Yilmaz et al.,2006).
近30年来,在理论及应用层面,有着大量的面波成像技术方面的研究成果问世.通过文献调研并系统梳理,围绕多道面波分析技术为主的浅地表面波成像技术的研究情况总结起来,包括但不仅限于如下方面:面波频散曲线正演计算(Chen,1993;Buchen and Ben-Hador,1996;凡友华,2001;凡友华等,2002)、面波场正演模拟(Xu et al.,2007;周竹生等,2007;熊章强等,2008;Zeng et al.,2011a)、复杂介质中的面波传播问题(Hevin et al.,1998;Zhang and Liu,2000;裴正林,2004;高广运等,2005;Bohlen et al.,2007;Cao et al,2007;鲁来玉,2007;Nasseri-Moghaddam et al.,2007;柴华友等,2008;Bodet et al.,2009;Zhang et al.,2009;秦臻,2010)、地形起伏对面波传播及其频散特性的影响(Hestholm et al.,1999;周红和陈晓非,2007;唐圣松,2009;Wang et al.,2012,2015a;汪利民,2013;Ning et al.,2018)、三维多道面波分析(Wang et al.,2015b)、多道面波记录的频散能量图生成方法(刘云桢和王振东,1996;Park et al.,1998;刘江平等,2003;宋先海等,2003;Song and Gu,2007;Xia et al.,2007;Luo et al.,2008;杨振涛等,2019)、面波频散曲线反演算法(Xia et al.,1999;Beaty et al.,2002;Ryden and Park,2006;Cercato,2007;Dal Moro et al.,2007;Song and Gu,2007;Song et al.,2007;宋先海等,2010)、多模瑞利波反演浅地表横波速度结构(Beaty et al.,2002;Xia et al.,2003;Luo et al.,2007;Song et al.,2007)、估计浅地表介质品质因子(Q)(Xia et al.,2002c)、瑞利波资料与折射资料联合反演(Ivanov et al.,2006)、从连续介质模型估计S波速度结构(Xia et al.,2006a)、含高速夹层模型 的 瑞 利 波 反 演(Calderón-Macías and Luke,2007)、含低速夹层模型问题(Lu et al.,2007;Liang et al.,2008;Mi et al.,2018)、瑞利波反演模型评估(Xia et al.,2008,2010)、瑞利波群速度反演(Luo et al.,2011)、勒夫波灵敏度分析(Zeng et al.,2007)、利用勒夫波反演改善S波速度估计质量(Safani et al.,2005)、低速层勒夫波反演(Safani et al.,2006)、地电与瑞利波及勒夫波的联合反演(Misiek et al.,1997)、利用勒夫波反演测量海洋沉积物的声学性质的横向变化(Winsborrow et al.,2003)、高频勒夫波数值模拟(Luo et al.,2010)等.
但利用以多道面波方法为主的高频面波方法对浅地表附近物质结构进行高精度成像的工作,一直以来都面临着一系列亟待解决的关键问题.多道面波方法采用规则的等间距长排列采集面波信号,其频散曲线反演结果是排列下方介质的平均横波速度,强烈的平均效应致使反演结果的横向分辨率难以提高(Mi et al.,2017),如何提高多道面波分析方法反演横波速度模型结果的横向分辨率是方法问世以来就面临的问题(Xia et al.,2005).面波频散曲线一般具有多模的特征,从频散能量图中进行频散曲线拾取时如何正确识别频散模式是一个复杂的问题,特别是对瑞利波而言,“模式接吻”现象严重(Xia et al.,2006b).而高速夹层(Calderón-Macías and Luke,2007)及低速夹层(Lu et al.,2007;Liang et al.,2008;Mi et al.,2018)存在时引起的“模式跳跃”(邱新明,2020;邱新明等;2021),使得频散曲线的拾取与模式识别工作变得更具挑战性.主动源多道面波分析方法采用人工震源激发地震波,能量有限,一般仅能获得浅地表附近30 m深度范围的横波速度结构.而这在应用于城市地下空间精细探测工作所要求的100~200 m深度范围时,由于有限的激发能量和强烈的环境噪声等原因,显得“力不从心”.基于互相关或干涉理论的背景噪声面波成像技术是最近十几年来迅速发展起来的成像方法,也是目前的研究热点,虽然其结果分辨率相比于主动源高频面波方法稍低,但却是主动源高频面波方法很好的补充.主、被动源联合勘探的思想,将极为有效地改善面波方法的成像深度与精度(王振东,1998;Park et al.,2006;Hayashi et al.,2013;张维等,2013).Cheng 等(2016)结合地震干涉法和MASW法提出了被动源面波多道分析方法(Multichannel Analysis of Passive Surface Waves,MAPS).在城镇“车水马龙”的噪声环境中,该方法的数据采集效率大幅提高且面波成像质量可比肩高质量主动源结果(Mi et al.,2022).常规的多道面波勘探,通常采用等间距布设的规则线型垂直分量检波器接收多道瑞利波信号,而在均匀各向同性水平层状介质中,瑞利波在垂直面内偏振轨迹为椭圆形态,因此其在径向和垂向上均有较强能量分布(Dal Moro et al.,2011).仅利用垂直分量检波器上获取的面波进行频散分析,不可避免地将会损失部分重要信息.对多分量信号进行频散分析,得到的面波频散曲线将更加完备与可靠(Dal Moro et al.,2015;Ikeda et al.,2015;Pan et al.,2018a).多道面波方法以地下介质模型的水平层状假设为应用前提(Xia et al.,1999),这极大地限制了方法在地下存在横向障碍物探测时的分辨率与应用效果.得益于计算科学和人工智能等技术的突破性发展,通过直接对波动方程进行求解,利用地震波的振幅和相位信息的面波波形反演方法在最近几年大放异彩(Pan et al.,2018a,2019;刘耀威等,2021),该方法绕开了面波频散方法所依据的水平层状介质假设,具有更为灵活的模型适应性,能有效改善传统面波方法低水平分辨率的问题.
针对上述问题,全球众多浅地表地球物理团队,开展了大量的研究工作,并在近几年取得了丰硕的研究成果,使我们对浅地表面波成像技术的认识更加清晰与完整,并极大地推动了浅地表面波成像技术在工程和环境领域的应用.本文就面波高阶模式波的应用、面波波形反演、被动源面波成像技术、多分量面波分析与应用、利用高铁噪声信号成像的高铁地震学、基于分布式光纤声波传感技术的面波高效率采集技术等方面的研究进展进行了调研与分析.国内虽然已有大量的学者开展了浅地表面波成像技术的研究,并有相当多的综述性论文发表.如夏江海等(2015)回顾了高频多道面波方法的发展历程,并对中国地质大学(武汉)浅地表地球物理团队在研究高频面波传播理论和应用中取得的部分成果进行了总结;徐义贤和罗银河(2015)介绍了噪声地震学方法(背景噪声面波成像技术)的发展历程,并详细综述了噪声源的分布情况和记录台站间距等因素对格林函数提取的影响,介绍了背景噪声面波成像技术在浅地表勘查上的应用现状;刘庆华等(2015)讨论了主动源多道面波方法与背景噪声面波方法中的空间自相关方法和噪声互相关方法三者联合的勘探思路与应用前景;宋先海等(2020)分析了浅地表弹性介质中瑞利波勘探方法的研究进展,并展望了其应用前景;邱新明等(2021)在较为系统地总结面波传播理论和相关方法技术的基础上,着重对多分量面波的研究现状进行了总结.但前述综述论文大多数是针对面波成像技术中的某一种方法,鉴于浅地表面波成像技术研究发展迅速,新的方法技术不断涌现,且部分原有技术不断取得新的突破,因此仍觉得有必要向国内学者特别是初入该领域的研究人员撰写此文介绍并推荐,希望浅地表面波成像技术能被推广应用到更多的领域.为了较为系统地总结浅地表面波成像技术的发展历程并保证论文的可读性,本文与前人综述不可避免地会有部分重复,但我们力求控制在最小程度.
1 高阶模式面波应用
传统的面波成像方法反演过程中利用的频散曲线,往往是振幅能量相对突出的基阶模式面波,但这仅仅适用于地下介质结构相对简单、地层速度模型为简单的水平层状、且速度随深度递增的情况.若地下结构相对复杂,存在明显的速度横向不均匀、速度各向异性、有软弱夹层或硬夹层存在时,仅利用基阶模式面波频散曲线反演,其效果则往往不理想.根据平面波理论,基于介质为层状模型的前提假设,由弹性波波动方程结合相邻界面的位移和应力传递公式、自由界面边界条件、无穷远处的辐射条件,即可导出面波(瑞利波或勒夫波)的频散方程.通过求解频散方程,可得面波随频率变化的相速度分布(Haskell,1953).相速度是频率的多值函数,即同一频率点处求解的面波相速度含有多个解,它们分别对应着由不同路径的体波干涉形成的不同模式的面波成分(Kennett and Clarke,1983).层状介质模型的瑞利波相速度取决于频率和各层纵波速度、横波速度、层厚度、密度等四种模型参数(夏江海等,2015),而勒夫波相速度与介质的纵波速度无关,仅与频率及地层横波速度、层厚度和密度有关(Aki and Richard,1980).本节我们首先简要地对面波理论相速度频散曲线计算方法的发展历程进行综述,在此基础上对含软弱夹层和硬夹层等特殊地层情况下的理论频散曲线及正演模拟记录提取的频散能量图的特征进行分析,之后探讨高阶模式波的特点,并根据文献调研结果总结其目前的研究现状.
1.1 层状介质中面波多阶模式频散曲线求解算法发展历程
描述地层介质弹性参数与瑞利波相速度或群速度之间的频散关系,可从弹性波波动理论出发建立,这样的关系方程在均匀弹性半空间模型中通常称为瑞利方程,在多层介质模型中一般称为频散方程或特征方程.针对特定层状模型,建立并求解这类方程是利用瑞利波频散性质进行勘探的正演问题.
Thomson(1950)和Haskell(1953)最早研究了面波在多层介质中的频散特性,他们在直角坐标系中,根据平面波理论,结合相邻层界面位移应力连续条件和自由界面边界条件以及无穷远处辐射条件,导出了层状介质中的瑞利波频散方程的矩阵形式.但该算法在计算高频端相速度结果时,容易出现数值溢出、精度丢失和不稳定等问题(Rosebaum,1964;Thrower,1965).为解决这些问题,1960 年代末期以来,研究者们对频散方程的求解方法付出了诸多努力.Harkrider(1964)研究了三种不同类型激励源下的瑞利波传播问题,同时建立了相应的频散方程.相对于各向同性层状介质而言,复杂介质中瑞利波传播机理研究,可从Biot(1956a,1956b)建立流体饱和多孔介质中地震波传播理论谈起,该理论建立后旋即成为研究多孔介质波动理论的基础.Jones(1961)根据Biot理论,研究并推导了三维饱和孔弹性介质中的频散方程,证明了瑞利波在饱和多孔介质中的存在,但因其仅考虑了一种压缩势,因此得到的并不是问题的通解(John,1961).Chiang等(1981)对饱和土中瑞利波进行了和John(1961)类似的研究.但之后Tajuddin(1984)的研究却给出了与John(1961)不同的结果.采用解析法和有限单元法,夏唐代等(1999)研究了流体/固体介质中的瑞利波传播问题,推导了相应的频散及位移计算公式.另外,夏唐代等(1992,1996)还研究了各向异性成层地基中勒夫波和瑞利波的频散特性.陈龙珠等(1998)根据其提出的饱和土中的弹性波动方程,推导出了饱和地基中的瑞利面波频散方程,并对瑞利波速度和衰减性与振动频率、土渗透因子等因素之间的关系进行了较为详细的分析.
与其它地球物理反演问题一样,正演是反演的基础,如何提高频散曲线正演计算的速度和精度,成为提高面波反演速度和分辨能力的关键因素之一.求解频散方程得到面波频散解的方法有两种,即传统解析法和数值解法.目前,在实际工程应用中,采用最多的模型为均匀水平层状介质模型,解析法为求解其频散方程的主要方法,其中应用最为广泛是传播矩阵法,包括Thomson-Haskell方法(Thomson,1950;Haskell,1953)、Schwab-Knopoff方 法(Knopoff,1964)、δ矩 阵 方 法(Thrower,1965;Waston,1970)、Abo-Zena 方法(Abo-Zena,1979;Menke,1979)、RT矩阵方法(Kennett,1974)等.Knopoff(1964)和Thrower(1965)分别针对频散方程求解过程中的高频有效数字损失等严重问题进行了深入研究,并提出了δ矩阵算法.Abo-Zena(1979)同样对高频有效数字损失问题进行了深入研究,并提出了另一种新型算法,他通过一系列与特征函数密切相关的4×4阶反对称矩阵的循环计算得到相应频散方程,使得该算法能有效解决高频数值不稳定的问题,且有着很快的计算速度,但美中不足的是计算频率存在上限,仅为20 Hz,无法满足浅层高分辨勘探的要求.也在同年,Menke(1979)对前者提出的反对称矩阵的物理含义进行了解释,在引入了D矩阵和E向量后导出了新的面波频散特征方程.该方法具有较快的计算速度,同时能有效地避免高频有效数字损失问题.之后,不少研究者均对传播矩阵法进行了改进,提出的改进算法使运算步骤得以简化,大大提高了运算速度(李幼铭和束沛镒,1982).陈云敏和吴世明(1991)结合δ矩阵算法特点,对Abo-Zena 算法进一步改进,改进的Abo-Zena 算法计算效率高,且将δ矩阵型算法的各项优点包含在内.Chen(1993)提出广义反射—透射系数法,这是一种能同时计算多层半空间介质面波频散曲线和本征函数的系统性有效方法.相比于前述方法,该算法有着极大的优势.首先,它是一种简单而完备的算法,可以同时确定相速度和相应的特征函数.其次,由于采用反射—透射系数,从本质上排除了增长项,所以该算法不仅像Kennett(1983)那样展示了简正模式形成的物理机制即相长干涉,而且在高频稳定性上优势明显.此外,该算法还很好地给出了基阶模式波的高频渐近解.张碧星等在Abo-Zena算法和Menke算法的基础上,考虑面波的柱面波特性,在柱坐标系下对层状介质中的面波频散问题进行了研究.他们采用3个矩阵的乘积形式表示Menke算法中的E矢量和传递矩阵F,大大简化了矩阵运算,且能有效避免高频数值不稳定的问题(张碧星等,1997;欧阳联华和王家林,2002).凡友华和刘家琦(2001)对前述各类算法进行细致研究和分析后,基于δ矩阵算法的传递思想,提出了柱坐标下的一种快速稳定的传递算法,并称之为快速标量算法.该方法仅需进行系列标量的传递与计算,不存在对复数的求解与传递,因此有效提高了运算速度,同时将计算频率的稳定上限提高到20 kHz以上.何耀锋等(2006)在Chen(1993)提出的广义—反射透射系数法的基础上,利用该算法探讨了含低速夹层模型中瑞利波频散曲线的求解相关问题.Gao等(2014)同样利用广义反射—透射系数法及波场数值模拟方法,探讨了高泊松比介质中出现非几何波的情况,并证明了这类非几何波即泄露模式面波,其速度约为均匀半空间横波速度的1.9倍.
相较于均匀层状介质模型,任意复杂介质中瑞利波频散特性正演问题远没有解决.少数研究者试图在均匀层状介质的矩阵法基础上进行拓展,大多数研究工作由求解精确的解析解转向求解近似的数值解(Alterlman and karal,1968),如采用Boundary Element方法、FE方法、FD方法、线性化散射方法、射线方法等进行数值模拟.而且,求解问题的广度也随之拓宽,已不仅仅局限于特征方程的求解,对瑞利波振幅和3D瑞利波散射等问题的研究也有所涉及.
1.2 软弱夹层及硬夹层等特殊地层模型多模式频散特征分析
为展示高频面波各模式的频散特征,我们在此分别设置四层速度递增模型、含软弱夹层模型、含硬夹层模型,如图1所示,模型参数设置如表1所示.采用交错网格有限差分法分别模拟各模型中传播的瑞利波(Xu et al.,2007;Wang et al.,2012)和勒夫波(Luo et al.,2010)波场.数值模拟的震源子波为主频20 Hz、延迟时间0.1 s的高斯一阶导数函数.在地表设置道间距为1 m、最小偏移距为4 m的48道垂直检波器和水平检波器分别接收模拟的瑞利波及勒夫波.采用高分辨率线性拉东变换方法提取各合成多道地震记录的频散能量谱,如图2和图3所示.

表1 模型参数表Table 1 Physical parameters for Plane-laered models of Fig.1
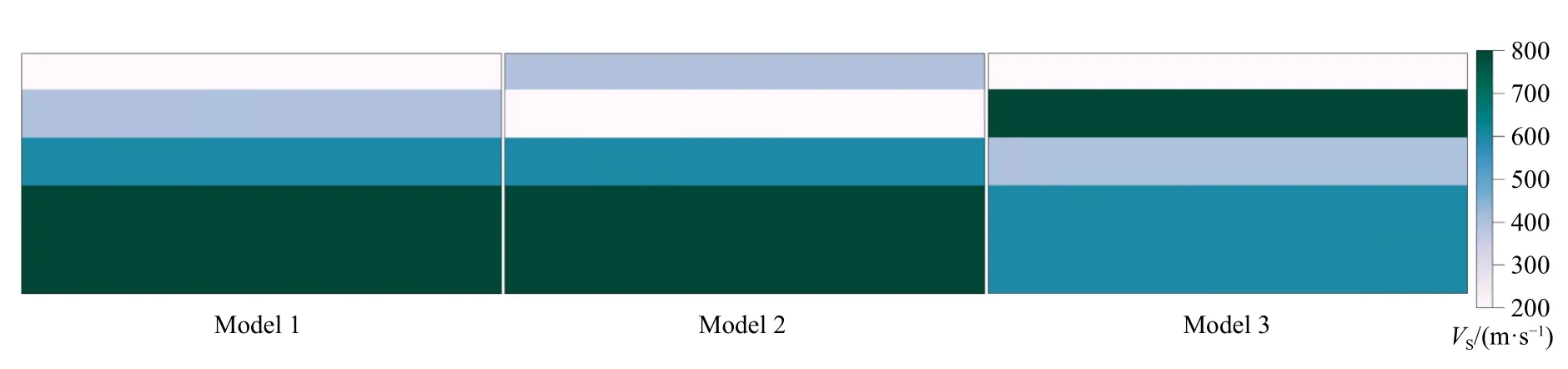
图1 四层速度递增模型(Model 1)、四层含软弱夹层模型(Model 2)、四层含硬夹层模型(Model 3)示意图Fig.1 Plane-layered model with vertically increasing veloceties (Model 1),Plane-layered model with soft interlayer (Model 2),Planelayered model with hard interlayer (Model 3)
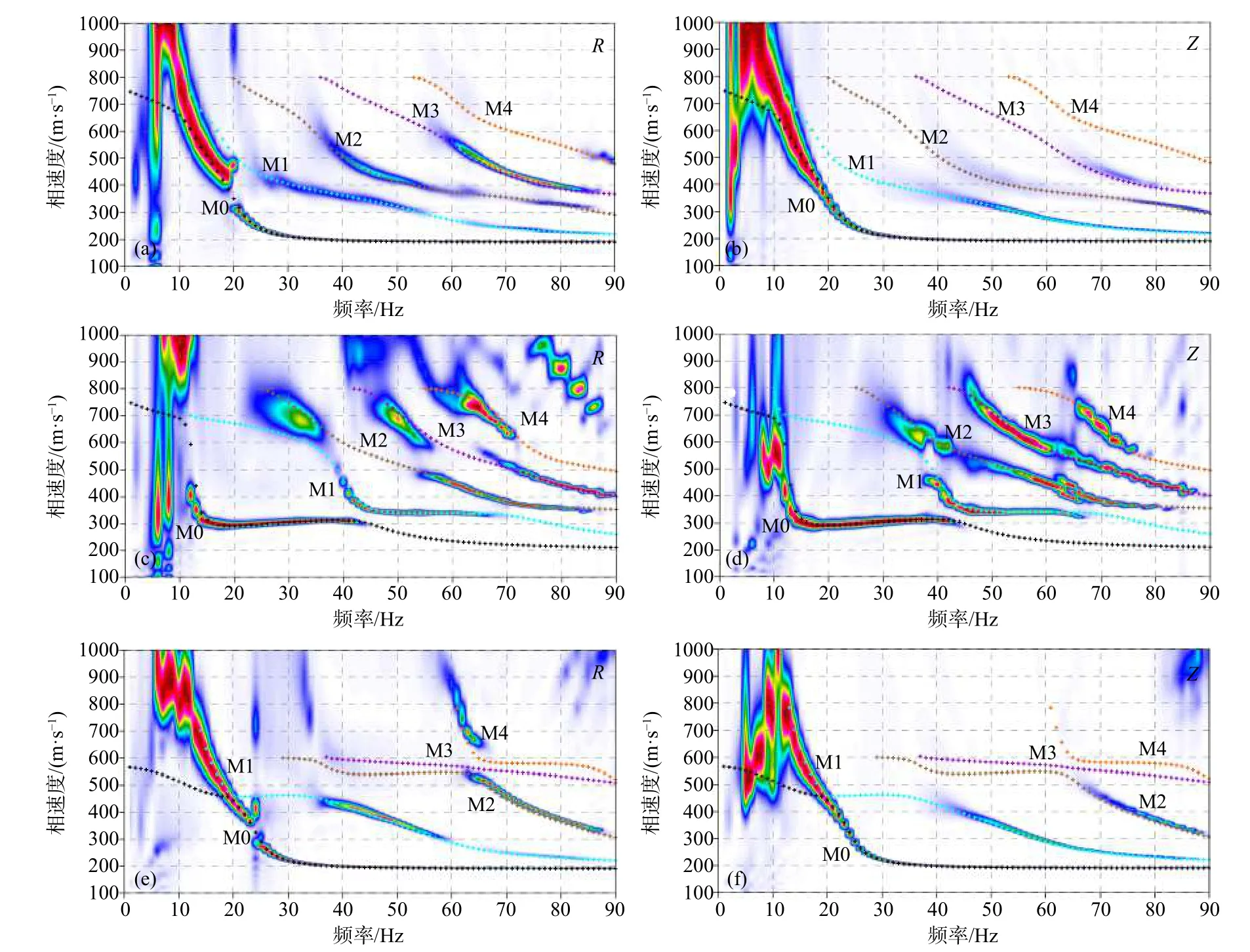
图2 四层模型垂直分量(Z)和径向分量(R)合成多道瑞利波记录频散能谱图.(a,b)四层速度递增模型结果;(c,d)四层含软弱夹层模型结果;(e,f)四层含硬夹层模型结果.M0表示基阶模式波;M1至M4分别表示对应的高阶模式波;图中彩色点线为快速标量传递算法(凡友华等,2002)所计算的对应模型的各阶模式理论频散曲线Fig.2 Dispersion energy curves for synthetic vertical component (Z) and radial component (R) of plane-layered models.(a,b) Represent the results for Model 1;(c,d) Represent the results for Model 2;(e,f) Represent the results for Model 3.M0 represents the fundamental mode.M1,M2,M3 and M4 represent the first to the fourth higher modes.The dot lines represent the corresponding analytical dispersion curves of Rayleigh waves,which were calculated by the fast scalar-transfer algorithm(Fan et al.,2002)
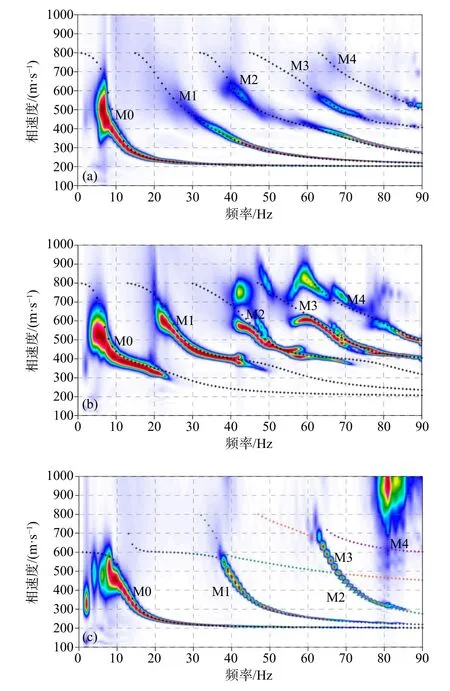
图3 四层模型切向分量(T)合成多道勒夫波记录频散能谱图.(a)四层速度递增模型结果;(b)四层含软弱夹层模型结果;(c)四层含硬夹层模型结果.M0表示基阶模式波;M1至M4分别表示各高阶模式波;图中点线为Knopoff算法(Schwab and Knopoff,1972)所计算的各模型多阶模式理论频散曲线Fig.3 Dispersion energy curves for synthetic transversal component (T) of plane-layered models.(a) Represents the result for Model 1;(b) Represents the result for Model 2;(c) Represents the result for Model 3.M0 represents the fundamental mode Love-wave dispersion curve.M1,M2,M3,and M4 represent the first to fourth higher modes Love-wave dispersion curves.The dot lines represent the corresponding analytical Love-wave dispersion curves,which were calculated by the Knopoff algorithm (Schwab and Knopoff,1972)
常规多道面波勘探通常采用垂直分量多道记录来提取瑞利波频散,而较少使用到水平分量(径向分量)记录.由图2a、2b可见,对于正常速度递增模型,Z分量(图2b)上,瑞利波基阶模式(M0)能量占主导,各高阶模式波能量随模式数的增大能量逐渐减弱,能识别的高阶模式共有3个,第四高阶模式波(M4)基本无能量.而对应的径向分量(R)记录提取的频散能量图(图2a)上,虽然基阶模式波能量依然占主导,且从低频至高频均有分布,但图中明显可以看到高阶模式波能量比垂直分量的频散能谱图上更加清晰,且分布的频段范围要更广,部分高阶模式(如M3)能量增强明显.这说明常规多道面波勘探仅利用垂直分量记录而舍弃水平分量记录的方式,会造成面波能量的损失.从图2a、2b中我们还可发现,不管是垂直分量记录还是径向分量记录,即使是对如此简单的速度递增模型,瑞利波各阶模式间也可能出现“模式接吻”现象,如图2中M0和M1在频段10~15 Hz间.低于10 Hz的频段,图中显示的能量为一阶高阶模式的能量,由于与基阶模式能量直接相连,且低频段再无其他明显能量趋势,因此在实际工作中很容易将之作为基阶模式频散拾取.这往往会造成反演结果中深部地层的横波速度被高估.“模式接吻”现象是造成瑞利波频散曲线模式识别困难的原因之一.
含软弱夹层模型的瑞利波频散能谱上显示出了与常规的速度递增模型不一样的特征.首先不管是Z分量(图2d)还是R分量(图2c),基阶模式波并非在所有频段上能量都占主导.从图中看,低于44 Hz的频段,基阶模式能量较强,而在高于44 Hz的频段,各高阶模式能量在部分频段上能量占据主导.其次,Z分量上高阶模式波能量表现出与速度递增模型不同的特征,能量并未随模式数的增加而递减.第三,“模式接吻”现象依然存在,且不仅明显存在于基阶模式(M0)与第一高阶模式(M1)之间,在各高阶模式之间也有明显的特征,这种现象在径向分量(R)上表现得更为明显.Mi等(2018)指出低速夹层模型中会产生低速层导波,在频散能量图中,低速层导波会干扰正常的瑞利波和勒夫波.低速层导波的每一阶在高频部分都会存在能量缺失现象,使得频散能量发生“模式跳跃”现象,这是由于低速层导波的短波长成分不能传播到地表造成的.如果低速层的横波速度比表层横波速度高,则导波只污染常规面波的高阶模式,不会与基阶模式波交叉;如果低速层的横波速度比表层横波速度低,导波能量则会与基阶面波交织在一起.这两种情况都会引起面波的模式误判.鉴于在该类模型中瑞利波各阶模式所表现的不同特征,若实际勘探中,仅拾取基阶模式波用于反演,不仅会导致反演深度变浅,甚至所反演的速度结果也可能不可靠(如被高估).而由于高阶模式能量在高频段较强,趋势明显,易于拾取,若加入一定的高阶模式频散参与联合反演,则能在很大程度上减轻以上问题的影响.
含硬夹层模型的瑞利波场频散能谱图上(图2e、2f),可见到与速度递增模型较为相似的现象,如基阶模式能量占主导;基阶模式波的高频段趋近于表层的瑞利波传播速度;基阶模式与第一高阶模式在20 Hz的频段附近存在明显的“模式接吻”现象等.与之不同的是,高阶模式数不多,从图中看不管是径向分量(图2e)还是垂直分量(图2f)的频散能谱,均只有两个明显的高阶模式波(M1和M2).通过与理论频散曲线对比可知,其中M1存在于低于20 Hz的低频段以及高于40 Hz的高频段,M2能量分布于65 Hz以上的高频段.另外,相比于垂向分量(Z),径向分量(R)上高阶模式波能量趋势更为明显,虽然M3依然缺失,但M4阶在部分频段上有所体现(图2e频段60~70 Hz间).高阶模式间的“模式接吻”现象依然严重,虽然部分高阶模式能量缺失,但从理论频散曲线上看依然明显存在,这依然会给实际勘探工作带来模式误判的风险.
综上可知,不同类型的速度结构模型上,瑞利波频散能谱有着不同的特征,理论分析并归纳总结这些特征,能有效指导我们的实际多道面波勘探工作,减少模式误判风险,提高勘探精度与深度.
相比于瑞利波的频散能谱,勒夫波的频散能谱相对简单.图3是前述三类模型上数值模拟得到的合成勒夫波记录对应的频散能谱图.在速度递增模型上(图3a),勒夫波频散能谱简单,几乎无“模式接吻”现象,且高阶模式波能量较强,趋势明显,截止频率位置较为清晰,各高阶模式能量分配较为均匀.这些特征都保障了频散曲线的精确拾取及后续的可靠反演.含软弱夹层模型的频散能谱(图3b)表现出与相同模型上瑞利波频散能谱部分相似的特征,如高阶模式能量较强,趋势明显,各高阶模式分别处在相应的不同高频段,不同的是各阶模式区分度清晰,无“模式接吻”现象.含硬夹层模型的勒夫波频散能谱(图3c)表现出与同模型瑞利波频散能谱(图2e、2f)相同的特征.首先从频散能谱图上看基阶模式波能量占主导,存在两段高阶模式能量,各模式能量分配较为均匀.其次,部分高阶模式缺失.从与理论频散曲线对比可知该模型的勒夫波频散能谱存在“模式接吻”现象,这种现象存在于基阶模式和一阶高阶之间,也存在于各高阶模式之间.特别需要注意的是M2阶和M3阶存在着最为明显的“模式接吻”现象,68 Hz以下频段相速度较大的能量段实为M3阶模式能量,而因其与M2阶直接相黏连,在实际工作中很可能将其直接作为M2阶拾取.由以上分析,我们发现虽然勒夫波频散能谱相对更简单,模式识别更容易,但地下介质的复杂度仍严重影响着勒夫面波的频散能谱特征.这也使得我们实际工作中,往往存在着模式识别困难,易发生模式误判等问题.因此,多模式、多分量面波勘探从理论与实际应用上的进一步推进显得尤为紧迫.
1.3 高阶模式频散曲线应用
如前所述,面波具有多模态,已有的研究表明面波基阶模式波对浅表层横波速度变化非常敏感,但其高阶模式波对更深的速度信息更敏感且敏感频段较宽,因此具有更大的穿透深度.基阶模式波与高阶模式波的联合反演能提高面波频散曲线反演的精度、增加有效反演深度并使反演过程更稳定(Xia et al.,2003;罗银河等,2008).关于高阶模式面波基本特性的研究始于上世纪末(Tokimatsu et al.,1992;Xia et al.,2000;张碧星等,2000;张碧星和鲁来玉,2002),人们发现高阶模式波的获取有时比基阶模式更加容易,且高阶模式波对地层速度参数变化的敏感性更强,这样的敏感性在深层更显著.这些认识为实现面波的多模式联合反演以增大反演深度、提升反演算法稳定性提供了理论指导,也让面波的频散曲线反演开始进入多模式联合反演阶段.Beaty等(2002)利用模拟退火法尝试了瑞利波的多模式频散曲线联合反演,获得了比纯基阶模式频散反演更可靠的结果,但由于全局搜索算法的计算效率太低,该方法在实际工程应用中不多.基于基阶模式和高阶模式瑞利波频散曲线的不同特点,Xia等(2003)尝试了利用多模式联合反演增加反演信息来减少面波频散曲线反演的多解性.含软弱夹层模型的频散曲线反演问题是面波频散曲线反演研究中的难点之一,Feng等(2005)尝试了基于遗传算法的多模式频散曲线联合反演工作,从其实际数据的反演结果看,软弱夹层信息得到了有效恢复,但该方法太过耗时,且不适用于层数大于五层以上的模型.基于连续小波变换,Tillmann(2005)尝试了多模式面波的走时反演,遗憾的是该方法在低频部分反演效果较差,且易陷入局部极小值.罗银河等(2008)利用阻尼最小二乘方法对一个六层介质模型进行多模式联合反演,取得了较好效果,其结果表明多模式联合反演有助于提升反演稳定性及精度.以上一系列的有益尝试,为更进一步深入揭示高阶模式波特征和更好利用高阶模式波实现浅地表介质横波速度高精度成像提供了理论指导.
野外实际地质条件远比理论层状模型复杂,某些地层由于沉积环境的差异或经过后期的人为改造等原因,会存在显著低速夹层现象,这类地下结构会造成所采集面波数据存在频散能量模式跳跃现象(张碧星和鲁来玉,2002).此时,基阶模式波并非在所有频段占波场主导地位,频散曲线拾取过程中容易误判模式,且仅针对基阶模式波的反演,所得结果可能明显失真.而在反演过程中考虑高阶模式波,则可有效降低反演的多解性,使反演结果更可靠、更稳定.为避免此类模型中的模式误判,Lu等(2007)提出了针对面波激发强度的多模式瑞利波反演方法,相比于仅反演基阶模式波频散曲线,新的反演方法具有更好的稳定性,并有效减少了反演的多解性(Socco et al.,2010).目前多模式面波勘探方法已成为浅地表环境与工程勘察中的常规方法,从信号采集、处理、到最终反演成像的整套技术流程已发展成型.
为减少频散曲线拾取过程中可能产生的模式误判现象,可靠的高分辨率频散能量图的产生至关重要.不少学者在此方面开展了大量的研究工作.Luo等(2008)在总结前述常规面波频散能谱算法的基础上,将频散能谱比拟为模型,时空域内的面波记录比拟为输入数据,引入地球物理反演概念和共轭梯度法求解过程,提出了高分辨率线性拉东变换方法(High-Resolution Linear Radon Transform,HRLRT).该方法有效提高了多模式面波频散能谱的收敛程度,减小了模式误判的可能性.而与之配套的反变换算法,能够有效地实现多模式面波的分离与重构,重构之后的各阶模式波频散能谱相比于重构前频段范围更为清晰,也更方便多阶模式频散曲线的准确拾取(Luo et al.,2009).基于复地震道分析方法,Parolai(2009)提出了一种新的估计多模式面波频散的方法,该方法适用于多道面波数据分析,且在接收道仅有两道时也适用.因此有望在不损失频散能量谱成像质量的基础上,提高多道面波分析方法反演地下介质横波速度结构的水平分辨率.通过假定多道面波信号在波速方面是稀疏的特征,利用L1范数正则化方法对该稀疏信号进行优化重构,得到信号幅值随波速变化的能谱图,Mun等(2015)提出一种基于信号表达和重构技术的面波频散能谱计算方法,文中结果表明该方法在高阶模式频散能量成像上聚焦效果良好,存在模式相干的情况下能较好地进行模式分离.Shen等(2015)详细比较了f-k变换法、τ-p变换法、相移法、倾斜叠加法、高分辨率线性拉东变换法等方法提取多道面波记录频散能谱的效果,并提出了一种改善传统频散能量成像方法低分辨率问题的有效策略.应用改善策略后的频散能谱图分辨率均与HRLRT方法一致.f-k变换法作为最早的面波频散能谱图计算方法,在浅地表面波勘探工作中发挥了重要的作用,但传统的f-k方法对面波基阶模式频散谱成像效果较好,而高阶模式能谱成像质量较差,难以识别.为解决这一问题,李欣欣和李庆春(2017)提出了一种改进的f-k方法.其模型验算结果和实际数据结果表明,改进的f-k方法不仅在高阶模式上成像质量较好,且可分辨的频段更高,有效保证了高阶模式波的提取.相移法(Park et al.,1998)是工业界应用最广泛、也最成熟的面波频散能量提取方法,但遗憾的是其在高阶模式波频散能量提取上效果略差.伍敦仕等(2017a)提出对多道面波记录各道信号与其他道进行互相关的同时进行相速度扫描叠加,最后再求和获得最终的频散能量谱的频散能量谱计算方法,该方法相对普通的相移法而言,改善了频散能谱质量,对噪声的压制能力也有所提升.之后他们又借鉴f-k域波束形成器原理,引入多重信号分类算法,将空间域信号分解为信号子空间和噪声子空间两部分并利用噪声子空间部分生成频散能量图(伍敦仕等,2017b),该方法能在排列较短时依然保持较高的相速度能谱分辨率,这对于横向高分辨率面波勘探具有一定应用价值.
为充分利用高阶模式波在横波速度成像上的优势,陈晓非院士团队近五年来在高阶模式面波理论研究、频散能谱生成及应用上开展了一系列的研究,取得了丰硕的成果(王建楠,2017;杨振涛,2017;戴文杰,2018;黎汉民,2018;李雪燕,2019;Wang et al.,2019;吴华礼,2019;吴华礼等,2019;杨振涛等,2019;李雪燕等,2020;苏悦等,2020;吴高雄,2020;詹望,2020;戴文杰等,2021).他们基于对检波器和震源之间格林函数进行频率—贝塞尔变换所提出的矢量波数变换法(Vector Wavenumber Transform method,VWTM)(王建楠,2017;杨振涛等,2019)有效地提高了高阶模式面波频散能谱的成像质量.这种方法不仅适用于主动源多道面波数据多模式频散能量图的生成,同样也适用于背景噪声面波场,不过在应用于背景噪声面波频散能谱计算时,它有了新的名字,即频率—贝塞尔变换法(Frequency-Bessel Transform method,F-J)(Wang et al.,2019).在应用于主动源面波数据时,相比于相移法和高分辨率线性拉东变换法,在采集道数相同的情况下,矢量波数变换法高阶模式频散能谱成像效果更佳,且具有更优越的抗噪能力(苏悦等,2020).众多实际勘探实例表明该频散能谱计算方法在主、被动源地震面波勘探中应用效果良好,能有效提高横波速度反演的精度(黎汉民,2018;李雪燕,2019;吴华礼,2019;吴华礼等,2019;Hu S et al.,2020;李雪燕,2020;吴高雄,2020;詹望,2020;戴文杰等,2021).另外,最近研究的利用汉克尔变换代替贝塞尔变换产生频散能谱(Xi et al.,2021)的方法,已被证明具有更高的信噪比(Li Z et al.,2021),可以压制频散能谱成像过程带来的“交叉伪影”.
2 面波波形反演
传统的面波勘探如多道面波分析方法基于面波(瑞利波或勒夫波)在层状介质中的频散特性,通过频散曲线反演估计层状介质的横波速度.为了快速稳定反演观测排列下方的一维横波速度结构,近30年来,大量线性局部优化和非线性全局优化算法被开发出来.局部线性优化算法如最小二乘法和奇异值分解算法(Xia et al.,1999;Li and Li,2016;Wu et al.,2019)、Occam算 法(Zhang et al.,2003)、基于最速下降法的波动方程频散曲线反演算法(Li J et al.,2019)等.但局部线性优化算法普遍存在对初始模型依赖性较强、容易陷入局部极小值、计算时需要求解偏导数获得梯度方向等问题,极大地限制了其应用效果与应用领域.为了克服以上问题,大量非线性全局优化算法被开发并利用在面波频散曲线反演研究中.如遗传算法(Lei et al.,2019)、模拟退火算法(Beaty et al.,2002)、人工神经网络(周晓华等,2011)、自然邻域算法(Sambridge,1999a,1999b)、广义模式识别算法(Song et al.,2008,2009)、混合演化算法(Song et al.,2012a)、粒子群优化算法(Song et al.,2012b)、差分演化算法(Song et al.,2014a)、种群迁徙智能优化算法(Song et al.,2014b)、反向追踪算法(Song et al.,2015a)、人工蜂群算法(Song et al.,2015b)、灰狼优化算法(Song et al.,2015c)、自适应混沌遗传粒子群算法(杨博等,2019)等.这些非线性全局优化算法的开发,极大地推动了水平层状介质中面波频散曲线反演技术的发展,扩展了其应用的领域.
但不管是线性化局部优化算法,还是非线性全局优化算法,都是基于介质模型的水平层状介质假设,因此仅能反演水平层状介质模型,对横向非均匀模型或存在局部不均匀体时并不适用.为了克服面波频散曲线反演的局限性,直接从地震波场正演模拟出发,充分利用波场的振幅和相位信息的全波形反演方法逐渐发展成熟,并开始在浅地表高分辨率面波成像工作中大放异彩.全波形反演的思想于1980年代由Tarantola(1984,1986,1988)首次提出,并最先成功应用于海上反射波地震资料,并被认为是地震成像工作的“终极武器”.鉴于陆地浅地表地震波场的复杂性,虽然这一思想极为先进,但一直以来并未在浅地表地震资料处理中获得足够关注.全波形反演的推广与应用,一直以来受限于其过于庞大的计算成本(Crase et al.,1990),但伴随近年来飞速发展的计算机技术及相应并行算法或快速算法的不断涌现,利用全波形反演思想实现地下结构的精细成像工作的条件已日趋成熟(崔永福等,2016).全波形反演通过拟合实测波形记录与波场正演模拟的波形记录,达到成像的目的,同时利用了地震波形的相位和振幅信息.若这一思想能用于浅地表面波成像工作中,相比于仅根据频散信息利用面波的相位特征将有极大的改进.相关的研究最先从全球或区域尺度的地球内部结构开始,Lerner-Lam和Jordan(1983)率先开始面波全波形反演研究,他们利用瑞利面波的相位信息反演了地下约200 m范围的横波速度结构.更大尺度上,Yomogida和Aki(1987)同时利用瑞利波的振幅和相位信息,通过波形反演方法研究了太平洋盆地的速度异常情况.Snieder等(1988)提出一种利用直达瑞利波相位和振幅信息重建地下横向不均性的大尺度波形反演技术,较早地利用了面波波形反演的思想实现了大尺度地球内部圈层结构的精细成像和速度各向异性研究.基于面波射线近似理论(Levshin,1985),Du(2002)提出一种多模态面波波形联合反演方法,该方法对强横向速度不均匀模型的结构重建具有良好的适应性,能用于解决大陆边缘、地堑、板块不连续界面等大尺度构造成像问题.以上方法主要适用于大尺度构造成像,其所利用的面波均为低频面波,其波长较长,对于地球浅地表结构成像来说,由于尺寸较小,以至于难以分辨,因此前述方法很难运用于浅地表结构精细成像.但随着全波形反演方法研究的不断深入,适合开展浅地表结构成像的面波成像方法也逐渐发展起来.
在浅地表横波速度结构成像研究中,Zeng等(2011b)采用遗传算法对数值模拟结果进行了二维介质面波全波形反演策略研究,探讨了面波波形反演在高精度横波速度成像上的可行性.Tran和McVay(2012)采用高斯—牛顿法在时间域内对面波波形进行反演,获得了地下20 m深度范围的横波速度结构,文中算例表明该方法明显优于常规多道面波方法的频散反演结果,对低速夹层模型及速度递减模型反演效果良好.Pérez Solano 等(2014)以及Yuan等(2015)分别采用加窗振幅波形反演方式和小波多尺度波形反演策略实现了二维水平地表弹性介质面波波形反演,并通过已知子波代替难以估计的实际震源子波,实现了二维两层和三层模型的理论模型面波波形反演试算.由于从实际面波勘探记录中对震源子波形态进行精确估计的困难性,他们未实现实际面波数据的波形反演工作,但其理论模型的结果,却也足以说明面波波形反演的巨大潜力.与之类似,Masoni等(2014)同样对面波波形反演的目标函数进行了优化,在一定程度上改进了反演效果.鉴于理论方面的研究逐渐趋于成熟,Bohlen等(2015)开展了瑞利波波形反演的实际应用效果研究,他们利用两套实际数据成功反演重构了一个河道沉积结构和一个横向速度变化剧烈的地下结构,重构效果良好.但两套数据表现出了不一样的特征,其中河道模型反演结果精度较高,而横向速度变化剧烈的模型精度较差,且将更高频率的数据加入反演则会引起反演过程不稳定.
前已述及,相比于瑞利波,勒夫波不仅在频散特征上更加简单,易于模式识别,且还因它的形成与纵波无关,因此不管是频散反演还是波形反演过程都更稳定,解的非唯一性更弱.Pan等(2016c)从时域上实现了勒夫波的波形反演,其数值模拟和实际数据算例表明整个反演过程稳定且结果可靠.同年,Wittkamp等(2016)开展了瑞利波和勒夫波波形的联合反演研究,其结果表明该联合反演算法能有效改善浅地表横波速度的成像效果,且联合反演还有助于对浅地表介质速度各向异性特征的研究与表征.类似的联合反演研究也有体波与面波之间的,如傅磊和刘四新(2016)提出一种基于交叉梯度约束的纵波初至与面波波形联合约束反演策略,反演过程中加入以纵波速度和横波速度的交叉梯度作为正则化约束项,使得二者在反演过程中相互制衡,从而实现了纵波初至波和瑞利波波形的联合反演.文中算例表明该方法能有效提高横波速度成像精度,并使反演过程更稳定.Köhn等(2016)和Groos等(2017)分别尝试了对简单的超声波实例数据和简单的三层水平层状弹性介质实际数据进行了瑞利波波形反演工作.Pan等(2018b)通过优化的真空近似法自由界面边界条件和交错网格有限差分方法相结合实现了起伏地表瑞利波和勒夫波的正演模拟,并以此作为正演算子,实现了二维起伏地形的瑞利波和勒夫波波形反演.其结果表明考虑起伏地形时,瑞利波波形反演和勒夫波波形反演重构浅地表横波速度结构的能力相当,而忽略地形起伏因素后,勒夫波波形反演效果优于瑞利波波形反演.在基于梯度的全波形反演中,目标函数的海森矩阵维度巨大,显式计算十分困难,管建博等(2021)借鉴逆散射理论的思想,给出了用于求解勒夫波波形反演的拟海森算子表达式,并提出相应的梯度预处理波形反演方法.
传统的面波波形反演通常使用波形差异的L2范数来最小化观测地震数据和合成地震数据之间的差异,达到反演横波速度模型的目的.但这这样的目标函数限制了面波波形反演的应用效果.Pan等(2020)提出了一种多目标波形反演(Multi-ObjectiveWaveform Inversion,MOWI)方法,该方法同时利用多个判别准则来量化和最小化数据的相似度,扩展了目标空间的维度.另外,从数据空间到目标空间的映射,使波形反演工作在模型空间探索上具有更高的自由度.新构建的多目标矢量目标函数,由三个不同的标量目标函数组成,能同时度量数据的波形、波形包络和幅值频谱的相似性,不仅考虑了基于道的波形和波包相似性,还考虑了面波的频散特性.此外,通过最优模型的方差可以对反演结果中的不确定度进行定量估计和分析.文中结果表明MOWI方法相比于传统的单目标函数波形反演算法具有更好的收敛性.
由于数据量大和目标函数的高度非线性等问题,全波形反演通常需要付出异常庞大的计算代价,却依然可能会收敛到局部最小值.为了缓解这些问题,Pan和Gao(2020)在多目标框架下重新制定了面波全波形反演的目标函数,提出了随机目标波形反演方法(RandomObjectiveWaveform Inversion,ROWI)来实现面波波形反演.数值模拟的综合测试结果表明,与传统FWI方法相比,ROWI方法的收敛速度更快,鲁棒性更强.将ROWI方法应用于在德国莱茵地区采集的实际数据,成功地重建了测区的主要地质特征,恢复了包含一条开挖后回填的沟渠的横波速度剖面,并将ROWI反演结果与探地雷达偏移剖面进行对比,进一步证明了ROWI估计浅地表横波速度结构的有效性.稳健性和不确定性估计是全波形反演中极具挑战性的两个问题.为了克服这些挑战,Pan和Gao(2020)提出了上述的随机目标波形反演(ROWI)方法,利用多目标框架和预处理随机梯度下降优化算法,每次迭代仅使用一个单炮记录,避免了使用冗余数据,降低了计算成本.之后他们(Pan et al.,2021)对该算法进行了进一步的改进,将原始的多目标函数分解为与单炮相关的子问题,并使用子问题的Pareto解进行权衡分析.利用改进的ROWI方法,对由德国莱茵地区采集的多分量面波数据进行波形反演,成功地估计了一个三维浅地表模型.测区内的回填沟槽结构被完美地勾画出来.这也是三维多分量面波数据的首个成功的全波形反演实例.
为改善面波波形反演的效果,除从反演的目标函数优化角度外,众多研究人员还从其他不同的方向进行了许多有益的尝试.Wang 和Richard(2017)利用基于模式分离技术的增强成像聚焦方法来抑制波形反演中的部分人为影响因素.Borisov等(2018)针对浅层速度不均匀问题,提出基于包络目标函数的反演策略,有效削弱了波形反演过程中的周波跳跃问题,该方法能有效地对复杂的浅地表结构进行精细成像.Xing和Mazzotti(2019)提出基于遗传算法的双网格瑞利波波形反演策略,通过数值模拟实例,验证了方法的可行性,其结果表明由于采用双网格格式,限制了未知数的个数,从而使得反演时间大大缩短.另外,该反演策略较好地预测了浅地表横波速度模型中的长波长分量,并证实了遗传算法即使在没有先验信息的情况下也具有较好的收敛性.震源子波形式对模拟波场的波形形态有着决定性的作用,Gao和Pan(2018)提出了一种基于面波模式分离的虚拟现实震源估计方法.该方法在常规的地震干涉测量前,先进行面波的多模式分离,再对分离后的各单模式波进行干涉测量获得相应的虚源记录,这样的方式有效地消除了由交叉模式产生的伪影.实际地震数据验算结果表明该方法对含有多模式的面波资料是有效的.Pan等(2019)成功将面波波形反演技术与多道面波分析技术相结合,实现了地层界面起伏模型的高水平分辨率成像工作.Liu Y H等(2021)同样利用全波形反演方法,结合多道面波分析结果和跨孔波速测试结果,实现了新加坡樟宜机场扩建工程回填土体中大型孤石的成像工作.周云腾(2019)结合了时间域和频率域波场模拟及反演的优势,利用交错网格有限差分法在时域实现高精度面波场正演模拟后将其转换到频率—波数域内,利用振幅谱信息构建多尺度反演目标函数,采用拟牛顿法进行反演估计最优的横波速度结构,模型试算结果表明该方法对初始模型依赖度较低,且具有较强的抗噪性(周云腾,2019;周云腾和张致付,2020).
地球实际地表介质极其复杂,远非完全弹性介质模型所能真实描述,介质的黏弹性或孔弹性特征等是否会对面波波形反演工作产生较大影响,是浅地表精细结构成像时必须考虑的问题之一.而浅地表常规二维全波形反演的大多数应用中,常常将地震波衰减因素忽略或将其视为被动建模参数.在此方面,Groos等(2014)率先开展了介质黏弹性对面波波形反演的影响研究,其研究成果表明,考虑黏弹性介质模型时,需先给出品质因子等信息进行约束,才能得到理想的波形反演结果,正确估计浅地表横波速度结构.Gao等(2020)探索了多参数黏弹性二维全波形反演方法的可行性及性能,其中P波和S波的速度和衰减因子以及密度被同时反演.数值模拟算例结果表明,黏弹性参数之间可能会出现多重串扰.重建的多参数模型结果中,横波速度的反演过程总是稳健的可靠的.而P波速度、密度等参数敏感性较弱.横波衰减因子异常可以部分恢复,但分辨率有限.利用该方法对Pan和Gao(2020)随机目标波形反演方法试算中使用的沟槽案例相同的野外实际数据进行反演计算,其中的小尺度回填沟槽被很好地描绘为低P波和低S波速度异常.加入衰减因子的同步反演,提高了纵波速度的重建效果.重建的横波衰减在浅层风化带衰减较大,而风化带之下衰减较弱.重建的P波和S波速度模型的变化与探地雷达剖面中观测到的反射率是一致的.由于不同参数之间存在潜在的串扰,以及瑞利波数据对不同参数的敏感性不同,全波形反演的多参数重建具有挑战性.基于二阶伴随方法的截断牛顿法计算逆海森矩阵,为减小不同参数之间耦合引起的串扰提供了一种有效的工具.Gao等(2021)将一种预条件截断牛顿方法应用于瑞利波波形反演,以同时反演包括纵横波速度、纵横波衰减因子及密度在内的多参数浅地表模型.首先通过对由这些参数引起的散射波场的研究评估参数之间的耦合关系,然后利用预条件截断牛顿法反演重建上述五个参数.在空间相关和不相关模型中的应用表明,预条件截断牛顿方法有助于减少串扰,提高多参数重建的分辨率,特别是对于衰减因子和密度参数等敏感性较小的弱参数效果最为明显.而由于纵波对瑞利波几乎不敏感,因此该方法也不能可靠地反演纵波衰减因子.
除上述主动源面波波形反演研究外,近年来发展迅速、已成为面波勘探领域研究热点的背景噪声面波方法所提取的被动源面波记录也开始被用于波形反演研究.Ridder等(2017)率先提出了一种针对背景噪声面波记录的频率域波形反演方法,该方法的提出为背景噪声面波成像技术的发展指出了一条与频散反演不一样的道路.
3 噪声面波成像
随着人类社会的发展,人们对其自身生存环境的质量要求不断提升,这使得污染严重的传统地震勘探生产活动受到了越来越苛刻的限制,探索以新型震源为代表的全新地震勘探方法的任务变得越来越迫切.一种能够达到甚至超越主动源地震勘探效果的被动源地震勘探方法,是地震学家们一直寻求和努力的方向.利用背景噪声信号研究地球内部结构和构造的方法为我们展示了这样的一种可能性.该方法目前已成为地震学界的研究热点,如《Geophysics》《Geophysical Prospecting》《Earthquake Science》等本领域国际期刊均分别以专刊形式展示过近些年来噪声地震成像技术领域所取得的一系列令人振奋的成果.国内的相关研究稍晚,但在区域性地壳或岩石圈尺度的应用研究上取得了丰硕的成果.徐义贤和罗银河(2015)对国内外背景噪声成像领域的研究成果进行了梳理,从背景噪声来源、噪声地震学的发展历程、基于背景噪声的全波场和面波场格林函数的恢复公式及影响因素等方面进行了综述.
地震背景噪声勘探的研究历史较为悠久,早在1950年代,著名地震学家安艺敬一教授就利用地震台站记录的噪声面波记录测定过覆盖层速度结构(Aki,1957).之后,1960年代美国为监视其他国家的地下核试验,建立了半径200 km以上的巨大地震观测台网(LASA),而为从观测的噪声地震数据中提取核爆引发的地震信息,Capon(1969)开发出频率—波数变换法(f-k)提取噪声记录中的面波频散信息,成功地对核爆场地位置进行精确定位,该方法后来在天然地震学研究中应用广泛.勘探地震学中相关噪声方法研究起源于斯坦福大学Claerbout教授领导的地震学课题组的开创性工作.Claerbout(1968)指出水平层状介质中噪声记录道的自相关结果等效于一个自激自收的地震记录道.后来他又提出通过将地表一定距离的两个地震台的噪声记录进行互相关运算,其结果可等效为将其中一个台站作为震源点激发一个地震信号而在另一个台站位置处接收所获得的主动源记录.因勘探地震学界一直以来采用人工震源的方式激发地震波获得地震剖面,Claerbout的这一想法长期未受到重视,因此被其学生称之为“Claerbout猜想”.虽然早期地震学界为证实这一学术思想,进行了各种尝试,但结果都不太理想(Baskir and Weller,1975;Cole,1995).转机出现在Claerbout猜想提出的25年后,Duvall等(1993)通过噪声互相关的方法获得了太阳外部圈层的三维流速结构图,发展出后来被称为“声学日光成像”的日震学新技术.日震学家抢在了地球物理学家之前验证了Claerbout猜想的正确性.最早的与地震勘探最为接近的验证实例来源于超声波检测领域,Lobkis和Weaver(2001)关于扩散超声场的工作从理论和实验两个方面证实了两个接收器之间的格林函数(即对脉冲源的响应)可以通过这些记录的时间互相关来恢复.这一概念即我们现在所熟知的地震干涉法,目前已有大量的相关研究成果问世,且已被推广应用到各类复杂介质成像工作中(Schuster,2001;Snieder et al.,2002;Wapenaar,2003,2004;Bakulin and Calvert,2004;Schuster et al.,2004;Snieder,2004;Wapenaar and Fokkema,2006).
截止目前,前述的绝大多数地震干涉法研究都集中在对自然环境噪声场上.这类自然噪声场,根据频带范围的不同,其产生的机制也是各异的.如早期应用最为广泛的频段在0.04~0.08 Hz的自然噪声(地脉动),主要是由于海洋与大陆架和海岸带的相互作用产生(Haubrich et al.,1963;Haubrich and McCanmy,1969).海浪产生的随机压力波动已被证明足以产生振幅相当大的微震(Hasselmann,1963).Longuet-Higgins(1950)推导了海浪对海底的压力/应力,指出了第一类地脉动和第二类地脉动的频率与海浪频率间的关系,以及压力扰动强度与水深间的关系,证实了第二类类型的微震能量,其峰值频率在0.1~0.16 Hz之间,是成对海洋涌浪非线性相互作用的结果.而更为低频的地球自由振荡噪声,频率在0.001~0.01 Hz的“嗡鸣”最为神秘,早期的研究将其归因于大气湍流(Nishida et al.,2000;Tanimoto,2001),而近期的一些研究结果表明其形成机制与造成初级或次级微震的机制相同,认为是大气—海洋—固体地球非线性耦合形成(Webb,2007,2008;Traer and Gerstoft,2014;Ardhuin et al.,2015).
前人研究表明天然源的地震背景噪声场主要由频率低于0.1 Hz的基阶模式面波所主导(Haubrich et al.,1963;Toksöz and LaCoss,1968;Ekström,2001).目前地震背景噪声面波层析成像技术已经发展成为一种稳健的成像技术,使地震学家能够成功完成局域小尺度(Brenguier et al.,2007;Lin et al.,2013a;徐佩芬等,2013b)、区域尺度(Shapiro et al.,2005;Kang and Shin,2006;Yao et al.,2006;Yang et al.,2007)和全球尺度(Nishida et al.,2009)的高分辨率多尺度地球内部结构成像工作.而在0.1 Hz以上的频率段,地震背景噪声场是基阶模式面波、高阶模式面波和体波的复杂混合波场(Bonnefoy-Claudet et al.,2006;Koper et al.,2010).已有的研究成果表明,从地震背景噪声波场中提取体波比提取面波更困难,尽管已经有不少成功的案例(Roux et al.,2005;Draganov et al.,2007,2009;Zhan et al.,2010;Poli et al.,2011;Ruigrok et al.,2011;Ryberg,2011;Lin et al.,2013b).因此,目前的地震背景噪声成像研究依然是以面波成像方法研究为主.这类型的研究在日本等多地震国家从未间断过(Matsushima and Okada,1990;Milana et al.,1996),目前已成为浅地表速度结构成像的热点研究方法(Hiroshi and Koji,2004;Shapiro et al.,2005),大量相关的研究成果不断被发表.根据三分量背景噪声记录,Hiroshi等(2004)用垂直/水平谱比反演了浅地表横波速度结构,与测井结果显示二者标准偏差在0.1 km/s以内,而最大误差也仅0.3 km/s.根据单台和台阵的背景噪声记录,Scherbaum等(2003)估计了德国科隆市的浅地表横波速度结构.采用背景噪声空间自相关法和频率—波数变换法,Estrella等(2003)测得了墨西哥城Ciudad大学内2 km深度范围内的浅层横波速度结构,对比结果显示两种方法所得结果较为一致.在小区域尺度长时间的背景噪声观测记录中,不仅可以通过互相关方法提取到清晰的瑞利波成分,而且通过时频分析等技术,还可以从中提取到纵波成分(Roux et al.,2005).另外,通过地震干涉方法,从交通噪声中还能恢复出反射的横波信息(Nakata et al.,2011;Nakata and Snieder,2012),Nakata等(2011)将这类反射信息与主动源记录的反射信息进行对比,验证了其可靠性.Tonegawa等(2013)采用空间自相关法处理来自日本海沟处记录的长时间背景噪声记录时,从中提取到了清晰的来自大约350 m深浅反射层上的反射横波信号.根据该反射信号,他们成功将其用于分析由大地震所引起的地下速度结构各向异性特征.比较有意思的是,地震干涉法不仅可用于背景噪声面波成像,针对主动源反射地震记录中的鬼波等虚反射记录(ghost)进行干涉计算,其成像结果可以有效用于浅地表的散射体定位(Harmankaya et al.,2013).
国内利用背景噪声面波方法研究浅地表地下结构的工作最早见于1980年代末,王振东(1986)对微动信号的空间自相关法和应用情况进行了介绍.Liu等(2000)利用背景噪声面波技术实现了地表60 m以浅范围的横波速度结构成像,并将成像结果与横波速度测井结果对比,证明了方法的有效性与可靠性.陶夏新等(2001)利用布设于厦门的微动台站记录的背景噪声记录,推断了该地50 m以浅范围内的横波速度结构.Satoh等(2001)通过地震背景噪声信息反演研究了台湾台中盆地1.4 km以浅的横波速度结构.利用北京市内多个场地布设的微动台阵记录的背景噪声信号,何正勤等(2007)估测了北京城区内3 km以浅的地壳浅部速度结构,为北京市地热资源开发中地热钻孔位置的确定提供了可靠依据,所指导的地热钻孔全部达到了设计的供热标准.陈棋福等(2008)和王伟君等(2009)利用高密度地震台阵记录的背景噪声面波信号,采用微动水平和垂直谱比法等方法,对北京市浅层地壳结构的场地响应和浅层速度结构进行了详细研究,所获得的参数可用于地震动模拟和地震灾害预防.徐佩芬等(2012)在深圳地铁7号线车公庙至上沙段区间,开展了交通繁忙、建筑物密集、干扰严重的闹市区内的背景噪声面波成像工作.采用空间自相关法,结合少量钻孔资料进行标定,成功对深圳地铁7号线目标区间段的地下花岗岩“孤石”位置进行了圈定.他们提供的视横波速度剖面结果表明,二维背景噪声面波成像技术是在闹市区内探测地下结构的有效方法.噪声中提取的视横波速度剖面除能直观显示岩性的纵横向变化,还能给出岩土风化程度判断的可靠信息,这可为工程建设提供基岩面深度、起伏等情况,以及为桩基设计提供相应的地球物理依据.同时,鉴于背景噪声面波成像技术在地层分层和隐伏断裂构造探测上的诸多成功案例,该方法目前已成为沉积盆地结构调查、地热勘查和隐伏地质构造探查的新的、重要的地球物理勘探技术.在岩性差异性相对明显的地层界面,背景噪声面波成像方法对地层分层深度的确定误差可以控制在5%左右(徐佩芬等,2013a).滑坡体的滑动面上下介质软硬程度明显不同,存在着较为明显的物性差异.鉴于城镇区域主动源地震勘探施工困难,及滑坡体等不稳定构造上方不宜大规模施工的原因,为探明巴东黄土坡大型滑坡体滑动面深度及数目等信息,Xu等(2013)在湖北巴东县由中国地质大学(武汉)挖掘的、用于监测三峡黄土坡大型滑坡体的隧道内,布设了48个流动地震台站,进行了28小时的地震背景噪声观测.通过地震干涉法获得了3~30 Hz的虚源地震记录,之后根据主动源多道面波方法原理,进行频散分析与反演估计横波速度结构.最终获得的横波速度剖面结果显示,黄土坡大型滑坡体下至少存在着两个特征较为明显的潜在滑动面.Pan等(2016b)在新疆西准噶尔地区利用线性排列的高频(4.5 Hz)地震台站,通过地震背景噪声观测,提取面波频散曲线,并反演得到一条70 km长、深度为1.5 km的横波速度结构剖面.该剖面刻画了花岗岩体的分布.Liu等(2018)利用地表微震监测阵列对水力压裂现场周围三维浅地表剪切波速结构进行环境噪声层析成像.Zhou等(2021)利用密集台阵面波层析成像和Cheng等(2021b)利用三分量背景噪声资料提取面波信息,获得浙江金华一地热场的精细横波速度结构.
以上研究结果均表明,在地震台站分布密集的地区,基于背景噪声互相关的层析成像方法,可以有效地获得浅地表局部二维相速度变化情况.但使用基于射线的方法或一维解析参考模型来实现特定路径的面波频散数据的直接线性化反演过程,会造成复杂介质中的波速估计存在偏差.而直接利用地震波形的伴随层析成像或全波形反演方法,虽然从理论上说是非常准确的,但计算成本太高,目前尚未获得大规模应用.为了平衡计算效率与计算精度,便于采用面波相速度及群速度频散信息开展多尺度层析成像,及克服由于路径覆盖不均匀而导致的反演问题的不适定性,中国科学技术大学姚华建教授团队研究开发了背景噪声面波直接成像方法(Direct Surface Wave Tomography Method).该方法是一种基于射线追踪的直接反演方法,通过对所有特定路径的面波频散数据进行单次反演得到最终的三维模型结构(Fang et al.,2015).应用于台湾台北盆地城镇环境噪声互相关,得到的短周期频散数据集的反演结果,验证了该直接成像方法在浅地表三维横波速度结构成像上的有效性(Fang et al.,2015).相比于传统的层析成像方法,该方法具有一些明显的优势:它不需要预先构建二维相(或群)速度图,便可反演获得三维参考模型;能对速度结构的横向变化情况进行约束;与全波形反演和伴随层析成像方法相比,具有更高的计算效率;具备多尺度成像的优势.该方法目前已被成功应用到城市浅地表三维地质结构探测(Li et al.,2016)、页岩气藏开发中的场地破裂过程监测(Liu et al.,2018)、储气库区域浅地表精细三维地质结构探测(王娟娟等,2018)、活动断裂带三维精细浅地表结构探测(Gu et al.,2019)等领域.
但噪声面波成像方法也存在着一定的缺陷,比如其分辨率相对较低.张维等(2012)尝试了主被动源面波成像技术相结合的方式,探测浅地表地下介质横波速度结构.通过在北京顺义、海淀及银川三地进行的三个实际勘探实例验证了方法的有效性,其结果表明主动源具有对浅地表介质较高的成像精度,但成像深度有限,而背景噪声面波成像方法虽然探测分辨率相对较低,但其探测深度可达百米甚至千米.在条件允许的情况下,应尽量通过两种方法相结合的方式,开展浅地表介质横波速度成像工作,这样即可得到准确可靠的浅地表横波速度,又可相应增大勘探的深度.为进一步研究主被动源面波成像联合勘探方法的观测系统方式和改善最终的成像效果,张维等(2013)在河北廊坊夏垫镇及云南玉溪等地分别尝试采用不同观测排列和相同观测排列,分别采集人工源和天然源面波记录,提取频散曲线后,联合反演浅地表横波速度结构.其结果表明,相同排列采集,可在不增加工作量的情况下,既能保证浅层较高的探测精度,也能有效拓展勘探深度.
随着我国城市化进程的进一步加速,大城市、超大城市的不断涌现,人们对城市地下空间开发利用的程度不断加大、加深,由此衍生出的对城市地下空间地质结构精细探测技术的需求也与日俱增.城市地球物理的概念在近年被提出,其核心的科学问题是采用何种技术手段建立起城市地下的高精度三维地质图件(陈颙等,2003).如何获取城镇环境地下介质速度场信息,除了发展无污染、无破坏性的绿色震源(如人工可控震源)以外,背景噪声面波成像技术可作为另一条优选路线.近年来已有大量学者利用城市内因建筑施工、车辆及行人引起的地震背景噪声,开展浅地表地下结构成像研究(Folger et al.,2005),均获得了很好的效果.采用背景噪声面波成像技术来研究城市浅地表地下结构,最大的优点是不必担心传统地震勘探时的噪声干扰,以及不必担心在城市环境内因爆破等扰民行为所引发的各种施工限制.
从背景噪声成像技术的发展历程看,方法上的进步首先归功于基本理论的发展,而理论的发展可来自不同领域(徐义贤和罗银河,2015).地震背景噪声成像技术发展至今,其基本理论已成熟,希望在理论上取得新的突破实属困难.但任何一门科学,当基本物理问题厘清后,科学水平的提升就主要集中在方法和技术的进步上了,噪声地震学的发展亦如此.早期虽然理论研究均基于噪声源位置和能量的随机分布与配置的前提条件,但后期的方法研究早已突破这样的限制,因为勘探地震学界最擅长于精细的数据处理技术研究.因此地震背景噪声面波成像技术的发展,将继续从传统勘探地震学中吸收数据处理上的先进思路,进一步提高成像效果(徐义贤和罗银河,2015).通过互相关或干涉方法恢复的经验格林函数的信噪比通常较低,提高经验格林函数信噪比是成像效果改善的最基本条件.在勘探地震学中我们通常采用叠加的方式来改善资料信噪比.这一方式在噪声地震学中同样适用,但直接地对分段后求取的经验格林函数进行简单叠加,信噪比改善程度与叠加次数间并不成完全的正比关系,叠加次数的增加在改善资料信噪比上存在上限(张宝龙,2013).为了改善格林函数的叠加效果,Cheng等(2015)提出基于原始信噪比进行加权叠加的思想,新的叠加方式有效地改善了最终的叠加效果,如图4所示为分别采用常规叠加方法和信噪比加权叠加后获得的虚源炮集记录.很明显,新的叠加方式极大地改善了叠加结果的信噪比.在武汉汉江边采集的背景噪声数据处理结果验证了该方式的可靠性,且高阶模式能量恢复效果良好.
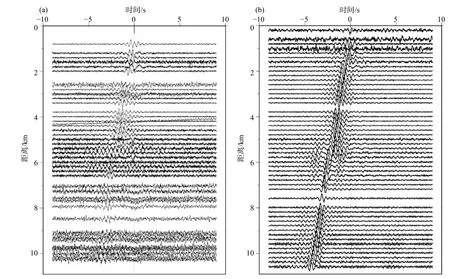
图4 叠加效果对比(修改自 Cheng et al.,2015).(a)传统方式叠加结果;(b)信噪比加权叠加结果Fig.4 Example of quality control using SNR weighting (modified from Cheng et al.,2015).(a) The CVSG with original stacking results;(b) The CVSG with stacking results that have been selected by quality control using SNR
“交叉伪影”是被动源面波频散测量中经常遇到的强干扰现象,对于沿公路或铁路线部署观测排列等存在明显双向噪声分布的情况特别常见.Cheng等(2018)对“交叉伪影”存在的物理基础进行了推导,证明该信号会在f-v域中的固定点上与真实面波能量相交叉,并提出一种基于f-k变换的数据选择技术来削弱该假频信号的影响,从而有效恢复高频信息.Xi等(2021)利用汉克尔变换产生的频散能谱,可以有效地压制频散能谱成像过程带来的“交叉伪影”,并被证明具有更高的信噪比(Li Z et al.,2021).
对超短记录时间的数据而言,噪声片段的选择和处理对成像质量影响很大.在足够长的一段时间内进行时间平均是满足噪声源随机分布要求的关键步骤.由于采集条件的限制或项目进度要求,城市地区的被动源噪声地震采集大多局限于超短的记录周期.由此造成的时间平均不充分,使得来自非平稳噪声源的贡献可能会严重影响叠加的频散测量结果,特别是对于低频段.Cheng等(2019)基于在期望的速度范围内具有高信噪比的输入数据的自动检测技术,给出了一个在tau-p域内实现的噪声地震记录面波频散测量的选择性叠加准则,并将其应用于频率大于1 Hz的高频交通噪声.模拟记录及实际数据算例表明,该判据准则能有效改善频散测量结果,削弱高频段信号失真的影响.如图5所示为对采集自湖南岳阳市境内京广铁路边的噪声地震记录,采用常规叠加方式和新的叠加准则后的面波频散测量结果.从图中可以看出,实施新的选择性叠加准则后,频散测量效果得到了显著的改善,特别是高阶模式波改善效果更为明显.
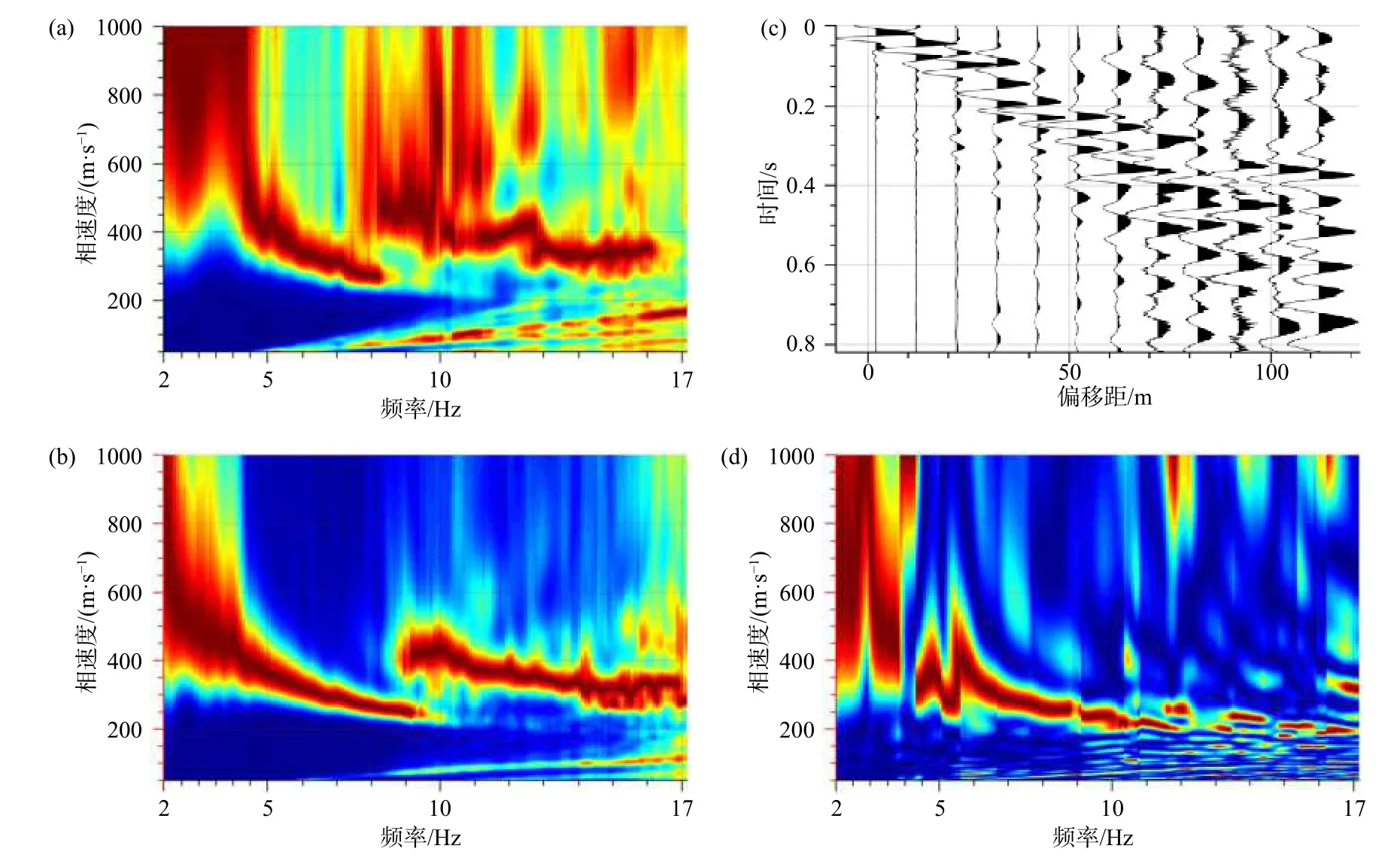
图5 实施选择性叠加判别准则前后效果对比(修改自 Cheng et al.,2019).(a)未实施选择性叠加准则获得频散结果;(b)实施选择性叠加准则后获得的频散结果;(c)同测线的主动源面波记录;(d)同测线主动源记录频散测量结果Fig.5 Comparison of dispersion measurement before and after data selection (modified from Cheng et al.,2019).(a) Dispersion measurement before data selection;(b) Dispersion measurement after data selection;(c) Wavefield of the active surface wave in the x-t domain;(d) Dispersion measurement of the active surface wave
从以交通噪声为主的噪声信号中产生相干信号,需要考虑噪声信号的方位效应,并给出合适的处理方案.为有效提高复杂城市环境噪声信号中提取的面波信号质量,Zhou等(2018)提出了一种基于互相关函数不对称性的环境噪声数据选择方法.将非对称系数定义为随机面波和无序面波的对数能量比来度量相关不对称性,并考虑两种对称函数来建立筛选条件.数值试验结果表明,该方法充分突出了双向同轴震源,消除了离线震源引起的高速异常.城市路面采集的三分量野外数据实例计算结果表明,该方法能有效地抑制随机噪声和假频信号,使面波频散能量趋势更明显,对城市双向交通噪声具有良好的实用性.Pang等(2019)提出了一种基于信噪比的自动数据筛选技术.三个野外实例研究的结果表明,该技术在保留成像质量较好的噪声片段的同时,可以去除非稳态噪声或假频严重干扰的噪声片段,从而显著地改善被动源面波能量的成像效果.因为城镇超短噪声数据往往不满足噪声源是随机平稳过程这一假定,Zhang等(2021)通过实际数据处理试验,提出不必使用谱白化处理超短噪声数据的观点.以上工作均基于2016年由夏江海教授团队开发的MAPS方法(Cheng et al.,2016),该方法目前已成功应用于城镇环境浅地表介质成像(Mi et al.,2022)以及地热(Chen et al.,2021;Guan et al.,2021;Ning et al.,2021)、矿产等资源勘查中(Pan et al.,2016b).MAPS方法的高效率来自于采用的数据采集系统为线型观测系统.但线型采集系统对环境噪声的方位特别敏感,因此测定噪声方位对于MAPS方法而言有时是必须的.Liu等(2020)在线性排列旁侧增加两个检波器,构成拟线性排列,提升了排列的方位覆盖范围,从而可以利用聚束分析方法计算噪声源的分布情况,进而获得了准确可靠的频散测量结果.Liu Y等(2021)在线性排列条件下,计算多道数据间瞬时相位的相干性,用多道相干性对互相关函数进行加权叠加.实测资料显示,该方法压制了来自排列内部的噪声源干扰,显著提升了面波信号的恢复.
从背景噪声记录中提取可靠的高阶面波信息的技术是噪声地震学家长期寻求突破的一项技术,而这项技术在最近取得了重大的进展.陈晓非院士团队近年来开发的频率—贝塞尔方法(Wang et al.,2019),不仅在主动源多道面波频散能量成像上效果良好,且能有效地从背景噪声记录经过干涉处理后获得的虚源记录中提取到清晰可靠的高阶模式面波信号.吴华礼等(2019)将该方法应用于日本关东盆地布设的MeSO-net台网记录的背景噪声数据,从中提取到可靠的多阶模式瑞利波频散曲线,并采用多模式联合反演获得了关东盆地沉积层和基岩层的横波速度结构,经与前人给出的日本综合速度结构模型对比,证明加入高阶模式频散信号参与反演后能有效减少反演的非唯一性,获得更为可靠的反演结果.李雪燕等(2020)对采集自上海市苏州河地区的城市微动信号,采用频率—贝塞尔变换方法提取出可靠的多模式瑞利波频散曲线,反演获得了70 m以浅的横波速度结构,经与钻孔数据对比,验证了反演结果的可靠性.戴文杰等(2021)利用该方法对采集自安徽巢湖滩涂的背景噪声数据进行处理,提取出了高质量的基阶模式和一阶高阶模式瑞利波频散能量,通过拟牛顿法进行频散曲线反演,其结果说明加入高阶模式频散信息后反演所得浅地表横波速度结构更为准确.前述研究均主要针对由垂直分量记录的背景噪声信号的处理,Hu S等(2020)对频率—贝塞尔方法进行了扩展研究,将其推广至适用于多分量噪声数据的面波多阶模式频散信号提取.
综上所述,背景噪声面波成像技术因其对震源的无要求、对施工场地无任何限制等特点,可应用于解决大量的浅地表勘查与监测问题,如地下空间开发利用前期的地下结构勘查和开发后结构稳定性的安全监测(Picozzi et al.,2009)、城市噪声监测与定位、滑坡等地质灾害的监测和预警(Renalier et al.,2010;Mainsant et al.,2012)、活动断裂调查(Brenguier et al.,2008a;Guan et al.,2021;Ning et al.,2021)、地热田勘探(Obermann et al.,2015;Lehujeur et al.,2016,2018;Martins et al.,2019,2020;Cheng et al.,2021b;Zhou et al.,2021)、火山活动监测 与 预 警(Sens-Schönfelder and Wegler,2006;Brenguier et al.,2008b)、工程施工场地土壤工程性质调查与土壤分类、地下水运移的实时监测、土壤液化判别(Nakata and Snider,2011)、地震活动对场地土性质改造研究(Xu and Song,2009;刘志坤和黄金莉,2010)、冻土和冰盖的季节变化过程监测(Meier et al.,2010)等.
4 多分量面波成像
伴随着微电子领域工业技术的发展,地震观测仪器与观测技术已有了长足发展.多分量地震检波器和地震仪的问世,使得地球内部岩石圈结构精细成像、浅地表岩土工程结构精细探测、深部油气探测等领域相继进入了多波多分量地震勘探时代.高精度数字地震仪和检波器的发展,使我们面波勘探中,采集高质量勒夫波信号成为可能,这为多道勒夫波分析技术的问世及在浅地表横波速度成像上的应用提供了保障,也使得近年来包括浅地表领域和壳幔结构成像领域中勒夫波方法的成功应用案例逐年增加(Levshin et al.,2005;Xia et al.,2012;Pan et al.,2016a).而通过多分量面波信号分析,实现瑞利波和勒夫波的联合反演可实现更加精细的浅地表横波速度结构成像(Dal Moro and Ferigo,2011).采用多分量地震观测方式,能以与单分量常规地震勘探相同的勘探成本,获取到更多的面波信息.相比于浅地表面波成像方面,多分量地震观测技术在油气田勘探、地震检测与预报等领域有着更加深入与广泛的应用(Vera et al.,2012;Lu et al.,2017).当然,这也极大地推动了多分量面波信号观测技术的发展与应用.关于多分量面波信号的利用方式,部分学者进行了一定的研究与探讨,取得了部分成果(Dal Moro et al.,2016,2018).整体上来说,多分量面波勘探理论上相对成熟,但应用研究尚处于起步阶段,国内更是鲜有报道(邱新明等,2021).
在本节,我们将对多分量面波勘探的研究现状进行简要总结.着重介绍多分量面波频散特征和椭圆偏振特征,以及多分量面波资料的采集、处理与反演方法.
4.1 多分量面波频散特征及椭圆偏振特征研究
不管是多道面波分析技术(MASW)还是面波谱分析方法(SASW),所分析的瑞利波数据均是针对的Z分量记录,因此传统的面波分析方法未能完整地描述面波在浅地表介质中的传播特征.随着多分量地震观测技术在油气田勘探、地震监测等领域的逐步推广与大规模运用,浅地表横波速度结构成像研究中,也开始进行了一些有益的尝试.由此,我们对浅地表层状介质中面波频散特性及偏振特征的认识更为清晰,建立起的浅地表横波速度剖面也更准确.
多分量记录中R分量和Z分量的面波成分主要为瑞利波,但瑞利波各个模式在R分量和Z分量上的表现特征却不是一致的.理论频散曲线的推导过程中,层状介质中瑞利波振动特征可以通过本征函数求解的本征位移表达,在任意频散点上水平方向和垂直方向的本征位移并不相同,两条曲线间存在明显的差异(Chen,1993).而在实际多分量面波记录中,R分量和Z分量上瑞利波不同模式能量也是分布不均的,这或是造成R分量和Z分量瑞利波频散特征存在差异的原因(Qiu et al.,2019).不同分量上瑞利波频散特征存在的差异,在一定程度上可以使各分量间频散特征实现相互补充,而获得一个更加完备和更加准确的瑞利波频散曲线,这一观点最先在油气勘探资料中得到印证,Ikeda等(2015)利用R分量瑞利波频散记录,补全了Z分量记录中原本缺失的高阶模式频散信息,获得了一个精确的、频带更宽的多模式频散曲线.完备、准确的频散曲线能极大减小模式误判几率,并有效提高反演横波速度的精度和可靠性(Boaga et al.,2013).从前文所模拟的四层数值模型合成瑞利波记录的频散能谱图上可见,不同分量的瑞利波不同模式频散能量在各频段上强弱不一.与本文模拟结果类似,Qiu等(2019)通过一个简单的两层速度递增模型,数值模拟了R分量和Z分量的瑞利波记录,并分别提取了相应的频散能量图.从研究结果看,传统的Z分量记录中,基阶模式瑞利波频散能量在相对低频段占主导,高阶模式能量相对较弱,且随着模式数的增加,能量迅速减弱.而R分量上基阶模式波能量缺失,各高阶模式波能量分别在不同的频段占主导,且各高阶模式低频截止频段附近能量相比于高频更清晰.由此可知,若将Z分量频散能谱结合R分量给出的高阶模式能谱,将有助于获取完备的瑞利波频散曲线.
切向分量(T)记录中面波成分基本以勒夫波为主,不同于瑞利波,勒夫波的频散性质与纵波速度无关(Aki and Richards,1980),因此勒夫波有着和瑞利波不一样的频散特征.研究表明勒夫波的频散具有如下特征(Xia et al.,2012;夏江海等,2015):首先,勒夫波的频散曲线形态更为简单;其次,勒夫波的频散曲线相对于瑞利波存在“模式接吻”现象的可能性较低(对绝大多数模型成立),因此不易出现模式误判;最后,勒夫波频散能量图上各阶模式能量分配较为均匀,且各高阶模式截止频率清晰.根据勒夫波的以上频散特性发展出来的勒夫波多道分析方法(Multichannel Analysis of Love Waves,MALW)(Xia et al.,2012),通过提取并反演勒夫波的频散曲线,获得浅地表横波速度结构.反演过程与瑞利波频散反演过程相似,但不同的是若同样采用最小二乘法反演,勒夫波频散反演对初始模型的依赖程度要低于瑞利波频散反演,且由于反演参数的减少,使得反演过程相对更加稳定.但T分量记录并非任何时候都能获得可靠的勒夫波记录,勒夫波的存在条件与折射SH波的形成条件一致(Luo et al.,2010;Xia et al.,2012),因此在软弱夹层模型中,地表T分量记录中难以获得高频勒夫波,故无法通过勒夫波频散反演方法恢复浅部软弱夹层速度结构.
除前述的频散特征外,面波在层状介质中的另一个特征即其偏振特征,已有的研究均表明层状介质中面波特别是瑞利波的偏振特征异常复杂(Aki and Richards,1980).瑞利波是椭圆极化波,其偏振方向随着深度的不同而不同(Xia et al.,2004).其各阶模式的极化特征却并非一致,前人研究发现实际勘探地震数据中,基阶瑞利波偏振方式为逆时针椭圆,偏振角度约为90°,而第一高阶模式瑞利波则为顺时针偏振,其偏振角度接近0°(Rene et al.,1986).这一特征,同样在被动源面波观测实验中也得到了印证(Ma et al.,2016).基于不同模式面波在偏振特征上的差异,可以设计偏振滤波器来实现面波的基阶模式波和各高阶模式波的波场分离工作(Gribler et al.,2016),类似的思想在油气地震资料处理中,早已成功运用于分离面波与反射波信号(Lu et al.,2010;Galiana-Merino et al.,2011).勒夫波的极化特征与瑞利波完全不同,因此实际地震信号中可基于此特征实现勒夫波和瑞利波信号的分离(Meza-Fajardo et al.,2015).以上分离方式针对天然地震及油气地震勘探中的低频面波成分(10 Hz以下)是有效的,而现有的研究表明椭圆偏振的特点不完全适用于高频段瑞利波(De Nil,2005;Dal Moro et al.,2017,2018).层状介质中各阶模式瑞利波的偏振椭圆旋转方向和椭圆率均是频率的函数,因此高频段瑞利波很难根据椭圆偏振特征差异实现分离(Boaga et al.,2013;Qiu et al.,2019),此时常规的做法是在频率—相速度域里,采用高分辨率线性拉东变换及其反变换的方法,实现多模式瑞利波场的分离(Luo et al.,2008,2009).
关于瑞利波偏振椭圆率的计算,Ikeda和Matsuoka(2013)给出了多模式情况的理论计算公式.由此人们认识到与频散曲线类似,瑞利波椭圆率同样也是频率的多值函数,不同模式的瑞利波的极化椭圆率存在明显的差异(Qiu et al.,2019).而这种差异与介质横波速度结构密切相关(Boaga et al.,2013;Knapmeyer-Endrun et al.,2017).近年来在天然地震及浅地表高频面波勘探上,均有较好应用效果的基于瑞利波水平分量和垂直分量频谱比的H/V谱比法,其本质即为瑞利波椭圆极化的频散特征,与常规的相速度和群速度频散特征类似,H/V谱比大小与介质泊松比有关(张立和刘争平,2013).García-Jerez等(2019)将H/V谱比值和频散曲线联合反演方法用于壳幔结构成像,得到了一个相对更加准确的地壳和上地幔速度结构.相比于常规的相速度或群速度频散曲线,瑞利波椭圆率在浅层结构探测上更加敏感(Lin et al.,2012).Mi等(2019)成功从多道面波记录中提取出瑞利波H/V谱比曲线,其研究结果表明H/V谱比的峰值频率和槽值频率对介质的纵横波波速比和界面深度非常敏感,因此有望利用该特征和频散曲线的联合实现准确反演介质速度及分界面深度(袁艺等,2016;Li G L et al.,2019),这对岩土工程上准确估计基岩面深度等工作具有重要意义(Dal Moro and Keller,2013;Yu and Liu,2015;Gouveia et al.,2016;张若晗等,2020).但截止目前,关于瑞利波椭圆率的研究和应用多基于基阶模式波展开,高阶模式瑞利波的椭圆率频散特征研究还处于理论阶段,其实用化是未来需要突破的方向之一.
传统多分量面波数据分析主要针对的是矢量地震波场中的平动信息,地震波在地下介质中传播的过程本质上是质点振动过程的传播,介质质点的振动方式除了平动外,还包含了旋转和变形两种方式.三维空间中,可根据旋转轴的方向将旋转分量分为三种情况,一般记为Rx,Ry和Rz.它们与三个平动分量(R、Z、T)一起构成了三维矢量波场的六个自由度的矢量观测数据(Li and Van Der Baan,2017),由此才能完整描述波场的传播特征(Lee et al.,2009).目前多分量面波研究主要基于平动分量开展,旋转分量面波频散特性的相关研究才刚起步(Lee et al.,2007,2009).研究表明,旋转分量面波的频散特征与平动分量存在差异(Sun et al.,2018),相比而言旋转分量上面波的高阶模式频散信息更完整,受噪声影响更小.天然地震观测上,通常利用单台地震仪的旋转分量计算获得旋转速率,利用平动分量计算获得加速度信息,综合二者即可获得面波的完整相速度信息(Igel et al.,2005;Lin et al.,2011),以及实现面波的模式识别与分离(Li et al.,2017).X和Y方向的旋转分量以面波为主,可根据这两个分量数据正演面波场,并用于对常规平动分量的面波去噪(Edme et al.,2014).另外,综合旋转分量和平动分量的六分量矢量地震数据,包含了地震波场的所有信息,通过多重信号分类等算法能获得六分量的偏振信息,提升了奇异值分解算法中协方差矩阵的秩,能有效分离时域上重合的波场,而这是仅对单台站地震数据采用平动三分量偏振分析的方法所无法实现的(Sollberger et al.,2017).
4.2 多分量面波资料的采集、处理与反演研究
瑞利波频散曲线形态复杂,存在“模式接吻”现象,在模式识别上有一定难度.勒夫波频散曲线形态简单,较少“模式接吻”现象,易于模式判别(Xia et al.,2012).但也因其频散曲线形态过于简单,其对地下结构精细刻画的能力不如瑞利波(Dal Moro et al.,2015).相同波长的瑞利波和勒夫波在深度上的敏感性不同(Yin et al.,2014),这也就造成即使是在同一地层结构上勒夫波和瑞利波频散特征的不同,故联合进行瑞利波和勒夫波的频散反演有助于获得精确的浅地表横波速度模型,特别是速度各向异性性质的获取.这样的联合反演研究在天然地震和背景噪声面波成像研究中最先成功应用(Levshin et al.,2005).如前所述,平动分量中R分量和Z分量上的瑞利波频散信息具有一定的互补性,T分量上记录的主要为勒夫波信息,因此采用三分量检波器(3C-Geophone)进行面波勘探的野外数据采集工作,可同时获得瑞利波和勒夫波信息,不增加额外的工作量,是浅地表横波速度结构精细勘探工作野外数据采集的最佳方案.
浅地表常规面波勘探中,瑞利波的激发一般采用人工锤击的方式,勒夫波的激发一般采用横向击板法.与多分量地震记录类似,按照震源激发方向与测线方向的相对关系,可将震源分为垂向力源(Sz)、径向力源(Sr)、切向力源(St)三类.其中垂向力源垂直地表向下,径向力源方向与测线方向一致,切向力源方向与测线方向垂直.多分量地震勘探中,常用的震源为多分量震源,这类震源能同时在各个方向上激发地震波,如3C Galperin震源,目前已在多分量面波勘探数据采集中成功运用(Husler et al.,2018;Pan et al.,2018a).与传统多道面波方法采用垂向震源和垂直分量检波器仅采集单分量瑞利波(Z分量)、用横向击板法和水平检波器仅采集单分量勒夫波(T分量)的方式不同,将三分量震源和三分量检波器相结合进行面波数据采集工作,可以得到共计9个分量的地震记录,其中5个分量上包含了面波信息(Foti et al.,2014;Pan et al.,2018a;邱新明等,2021),各分量情况详细见表2.综合分析各分量上面波的频散特征,并进行频散曲线的联合反演,可获得更为精细和准确的浅地表横波速度结构(Morton et al.,2017).
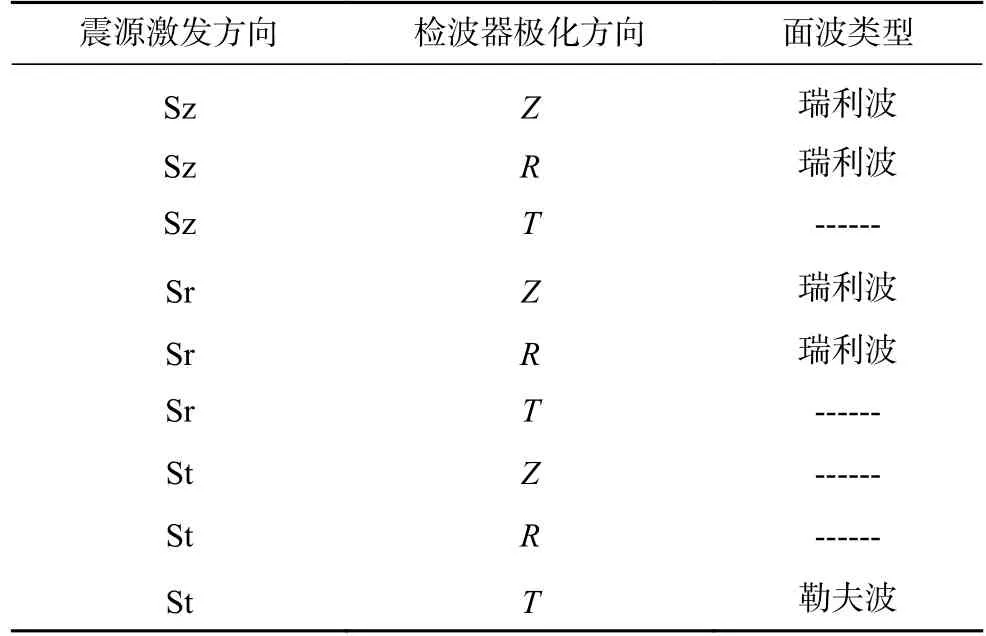
表2 3C震源与3C检波器联合激发与接收的多分量地震数据中面波类型Table 2 Surface waves types stimulated by 3C sources and acqusited by 3C receivers
在多分量面波信号的频散特征提取上,为获得最佳的结果,不少学者从不同的角度进行了众多尝试,取得了一定的进展.基于R分量和Z分量面波频散上的互补性,Dal Moro和Ferigo(2011)提出对分别提取的两个分量的频散曲线进行组合,可获得一个相对更为完备的频散曲线用于后续的反演.这种方式在一定程度上提高了瑞利波频散曲线的拾取精度,并扩展了能拾取的有效频段范围.但这样的方式,并不太适合横向非均匀模型.对于存在强干扰的情况,由于模式识别的困难,反而容易使拾取的频散曲线结果不正确.为了减少类似的人为因素的影响,Pan等(2018)认为将各分量瑞利波频散能谱进行叠加,能有效提高瑞利波频散能谱的精度.但这样的叠加要求叠前各分量所包含的频散信息是一致的,否则难以达到预期的叠加效果,因此这种叠加方法并不适用于各分量频散信息存在较大差异的情况.鉴于R分量与Z分量瑞利波频散能谱在一定频段上具有互补性的特点,Xu和Mikesell(2017)探讨了利用R分量瑞利波频散曲线来提高传统Z分量记录瑞利波频散曲线提取精度的可行性.而Qiu等(2019)另辟蹊径,将R分量和Z分量组合为复矢量,再采用高分辨率拉东变换算法(Luo et al,2008)提取该复矢量数据的频散能量谱.复矢量频散能量提取方法,在频散能量提取上能一定程度上削弱噪声干扰,避免模式误判,获得相对可靠和更完备的频散曲线.目前的研究仅表明在同震源情况下的平动分量上R分量和Z分量的瑞利波频散能谱具有一定互补性,而对3C震源与3C检波器联合激发和采集的9分量地震记录,并未明确该特征,因此该方法是否适合同时处理其他分量的数据,尚待深入研究.
多分量面波频散曲线的联合反演,能有效提高反演结果的精度与可靠性(Mi et al.,2020).虽然部分分量的频散能谱存在一定的互补性,但直接利用这种互补性,仅能一定程度上对反演结果的改善有所帮助.为充分利用各分量面波的频散信息,Dal Moro等(2015)分别针对垂向震源激发的平动R分量和Z分量以及切向震源(St)激发的T分量记录,构造了3个目标函数,采用Pareto优势准则优化求解,用于多分量面波频散曲线联合反演.这种新的多分量面波频散曲线联合反演的思路,为有效利用多分量面波的完备频散信息,实现浅地表横波速度结构精细刻画指明了道路.除此之外,袁艺等(2016)尝试了基于自然邻域算法的瑞利波频散曲线和垂直—水平谱比曲线的联合反演;Li G L等(2019)采用蒙特卡洛反演方法进行了同样的研究.Pan等(2021)从全波形反演方面提出了另一种新的解决方案,他们构建了一个三维随机目标函数,并成功实现了三维9分量面波数据的波形反演,数值模拟结果及实际9分量数据结果,均表明该方法有着良好地刻画浅地表横波速度结构的能力.
5 其他进展
5.1 高铁地震学
与人类活动相关的地震背景噪声所处的频段相应来说要更高,通常在1 Hz以上频段,这类型噪声通常表现出明显的周期性日变化(Bonnefoy-Claudet et al.,2006),如列车运行时产生的震动信号等,均具有如此特点.以往对列车振动的研究集中在其对地震台站监测的干扰,以及对铁路附近建筑物的破坏方面,目的是更好地理解列车振动的产生和短程传播机制,解决铁道附近建筑物的安全问题,很少将列车振动视为一种震源用于探测地下结构的研究.关于铁路列车运行时产生的地震动信号的研究从2001年就已开始(Ditzel et al.,2001),且近些年来随着高速铁路建设里程与运行车次的逐年递增,国内外类似的研究越来越多,这些研究包括基于动车响应积分表示来计算动车位移(Ditzel et al.,2001)、多轮轨结构的相互作用对高频轨道振动记录的影响(Wu and Thompson,2001)、路基和铁路路堤振动响应的测试方案,及数值预测模拟模型和相应的有效地面振动补偿措施(Kaynia et al.,2000)、高速列车高速通过铁轨时的自由振动和轨道响应(Degrande and Schillemans,2001;和振兴和翟婉明,2007)、列车振动信号用于浅层结构成像研究初探(陈棋福等,2004;李丽等,2004)、列车振动中等距谱线的显著特征及其产生原因(Fuchs and Bokelmann,2018)、列车振动产生的面波特征分析(翟培合等,2008)、高铁地震信号与列车运行速度和观测位置之间的关系(徐善辉等,2017)等.所谓的高铁地震信号指的是列车运行时车轮与铁轨之间发生挤压、碰撞和摩擦等产生的震动,在地下介质中以地震波的形式传播出去而被观测检波器所接收到的这部分震动信号.高铁地震波信号中蕴含着列车、铁轨、路基的基本信息,能够作为动态监测高铁运行状态的新工具,同时早期的研究也让人们发现高铁地震波监测在浅地表地下结构成像上的巨大潜力.
针对该类噪声的地震干涉法应用实例相对较少.据我们文献调研所知,Matsuoka 等(2006)和Shiraishi等(2006)分别首次尝试针对车辆运动产生的噪声利用地震干涉法实现了浅地表地下结构成像.Halliday等(2008)同样从车辆噪声记录中恢复出面波记录.Miyazawa等(2008)从井中观测到的来自井顶周围的机械设备振动引起的噪声记录中,成功恢复出垂直传播的P波和S波记录.Nakata 等(2011)从铁路和公路的噪声记录中,成功恢复出包括折射波和反射波的横波记录以及勒夫波记录.Behm和Snieder(2013)以及Behm等(2014)也分别从高速公路边记录的高频地震背景噪声记录中提取到清晰的面波场.另外,与之类似的,油气勘探过程中利用钻孔掘进时产生的随机噪声实现地下结构成像的案例,也是相当成功和引人注目的(Rector and Marion,1991;Poletto and Miranda,2004).
Quiros等(2016)于2014年5月利用布设于新墨西哥州贝伦附近伯灵顿北圣达菲铁路(BNSF)繁忙路段的100个道间距为25 m的垂直分量检波器,以250 Hz的采样率记录了连续120小时的铁路噪声信号,成功恢复了体波反射及面波信号.Draganov等(2006)及Forghani 和 Snieder(2010)的研究均明确指出了震源分布在地震干涉测量中的重要性.理想情况下,对于使用干涉测量法的近垂直反射成像,源的最佳分布位置在接收阵列的下方(Draganov et al.,2006;Ruigrok et al.,2011),而与之相反,列车源被限制在地表,因此其大部分能量在我们的接收排列中是沿着水平方向传播的,这对于恢复在水平方向衰减较慢的面波信息极为有利.Zhan等(2010)及Poli等(2011)分别基于长达6个月和1年的长时间地震背景噪声观测记录,获得了Moho面广角反射剖面,而Quiros等(2016)的研究未能恢复到深层反射记录,其部分原因应与观测记录周期较短有关.但Ruigrok等(2011)根据在埃及东北部阿布哈拉迪格盆地上空收集的大约40小时的地震背景噪声数据,恢复出来自Moho面的反射信息.当然,他们将其成功归因于浅地表噪声源距离足够远,以至于由于地壳和地幔的反射信号能以近垂直的方式入射到接收阵列上.因此,Quiros等(2016)认为希望通过铁路噪声实现深反射信号成像需要更大的偏移距及更长的记录时间.而相比较而言,其中面波信号却恢复得非常成功,可见高铁信号是一种非常好的面波能量来源,通过频散曲线反演,具有实现地下结构精细探测的巨大潜力.
此外,不管是对壳幔尺度(Bensen et al.,2007)还是区域尺度(Lin et al.,2013a)而言,相比于常规意义的微震干涉,由列车噪声所恢复的面波信号在高频段(1~14 Hz)更显著,前者频段通常在0.05~2 Hz范围.如图6所示为Quiros等(2016)所恢复的面波信号的一个范例.图6b所示频散能量图中清楚地显示成功恢复出了面波的基阶和一阶高阶模式能量.采用0~8 Hz频段内未发生“模式接吻”的基阶模式波反演得到的1D横波速度结构(图6c).因为面波反演的横波速度结构只反应了地下很浅的一部分结构信息(通常小于200 m,或0.2 s的双程旅行时间),故他们恢复的面波剖面未能和其所恢复的体波反射剖面完全对应,但却是对体波反射剖面不能很好地成像浅地表部分的一个最好的补充.且从虚拟炮集记录得到的纵波速度信息(约2 km/s)与面波频散反演的横波速度信息(1 km/s)是高度一致的.这一研究结果与Nakata等(2011)同样利用高速公路和列车噪声成像的成果高度一致.与传统的微震干涉结果相比,轨道交通噪声的互相关虚拟炮集在更高的频率上表现出较强的频散面波能量.且还能在一定程度上恢复部分潜在的体波(P)信息,用于实现地下结构的反射/折射波成像,虽然利用这类噪声互相关产生的反射剖面仅能达到1 km左右的深度,但原则上说可以通过叠加技术或更有利的观测系统(如大孔径)来获得更大的勘探深度和信号保真度.
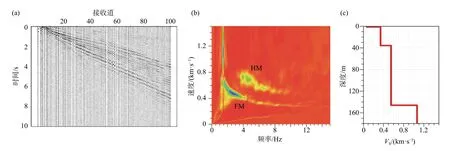
图6 (a)由铁路列车噪声信号所恢复的虚震源面波炮集;(b)从图(a)所示的虚震源记录中提取的含基阶模式和高阶模式的面波频散能量图;(c)反演图(b)中0~8 Hz基阶模式频散曲线获得的1D横波速度模型(修改自Quiros et al.,2016)Fig.6 (a) Virtual-shot gather with station 5 as the source;(b) Dispersion curve for the virtual-shot gather at receiver 5,with the fundamental mode (FM) and a higher mode (HM) labeled;(c) 1D shear wave velocity model obtained from the inversion in the frequency range 0~8 Hz of the dispersion curve from the fundamental mode (modified from Quiros et al.,2016)
我国高铁的发展虽然比发达国家晚了近40年,但在党和国家的领导下,经过几代人的持续奋斗,实现了高铁里程和技术上从无到有、从追赶到并跑、再到领跑的历史性变革(陆东福,2021).两万五千多千米的高铁纵横延展在祖国大地上,这是极为震撼的,但在地球物理研究人员的眼里,行进中的高铁同时又是一种全新的震源类型,其确定长度和荷载及近匀速运动使其具有可重复震源特征.其特有的宽频带分立谱特征,为高铁附近浅地表结构和物性高精度探测提供了条件.同时,纵横交错的高速铁路分布为大陆浅层高质量成像及地震预测预警研究提供了所需要的均匀分布的震源.鉴于此,由中国科学院地质与地球物理研究所、北京大学、西安交通大学、北京化工大学等高校和研究所的地震学相关研究团队于2018年成立“高铁地震学联合研究组”,开展高铁地震信号相关理论及应用方面的联合研究工作.目前该联合研究组在高铁地震学领域所取得的一系列令人振奋的研究成果,已于2019年分别以专辑的形式发表于《地球物理学报》和《北京大学学报(自然科学版)》上.这极大地推动了这一新学科方向的发展与应用.2021年科技部基础研究司也将该研究方向列入了“变革性技术关键科学问题”的重点专项优先支持方向.后文我们根据该联合研究组所取得的相关成果,介绍我国高铁地震学领域的相关研究成果和发展情况.
为了解高铁地震信号及波场特征,探究其在路桥检测、浅层勘探和深层探测中的应用,作为“高铁地震学联合研究组”主要研究团队之一的北京大学宁杰远教授团队从2018 年开始相应的数据观测和研究工作,分别在广东深圳和河北保定地区开展了多期观测任务.其中在河北省容城县附近的京广高铁沿线,利用由 200多个短周期仪器和 22个甚宽频带仪器组成的观测台阵,进行前后两期共一个多月的高铁地震观测,获得了近 50 万条高铁地震记录(温景充等,2019a).基于这些实测高铁地震观测记录,该团队从理论和方法等方面展开了一系列的研究,取得了丰硕的成果.这些成果涵盖了移动线源Green函数计算方法研究(曹健和陈景波,2019)、高铁地震信号的属性提取及聚类分析(蒋一然等,2019a;刘磊等,2019)、干涉成像方法初探(鲍铁钊等,2019;张唤兰等,2019)、信号分立谱特征及其与列车车厢长度和运行速度之间的关系(王晓凯等,2019a,2019b,2019c)、高铁振动激发纵波和横波的震源子波时间函数表达式(张固澜等,2019)、利用高铁地震信号的全波形反演建模及属性变化监测(胡光辉等,2019)、基于双台法和旋转法提取高铁地震信号中的面波频散信息(温景充等,2021)、高铁地震信号的时频谱特征分析(包乾宗等,2019)、高铁激发的远场波场模拟研究(温景充等,2019b)、高铁波场的等效震源时间函数反演研究(温景充和宁杰远,2019)、高铁地震信号的4D时频分析方法(蒋一然等,2019b)等.
综上研究成果,将高铁地震学方法与噪声地震学方法相结合,利用铁路和公路等方向性噪声源,进行面波格林函数恢复、并用于浅地表横波速度成像的方法,在水文、环境、工程等浅地表结构勘查上极具潜力,能以相对较低的勘探成本实现较大范围上的浅层地下结构成像.
5.2 分布式光纤声波传感技术(DAS)
高频多道面波方法因利用的是高频段(2 Hz以上)面波(Xia et al.,1999),数据采集时在时间和空间上的采样率要求较高,因此大区域开展高密度高频面波观测面临着诸如仪器布设与安全等一系列问题,采集成本太高致使方法的大规模应用受到了限制.而近年来,随着光纤传感技术的发展,一种新的地震观测技术让上述问题得以解决.当地震动在地下介质中传播时会引起介质质点发生位移而产生形变,埋设于地下的通讯光纤同样会因此产生一定的形变,这样的形变会使得光纤介质内部光信号的传播受到一定的影响.分布式光纤声波传感(distributed acoustic sensing,DAS)技术通过对光纤中传播的光信号调制解调,探测激光脉冲在光纤内部散射产生的瑞利后向散射信号的相位变化,实现光纤轴向应变的测量.光纤的每一小段可以等效为一个单分量应变仪(Benioff,1935),用于探测地震波场引起的应变.该技术目前已经被成功应用到地震勘探领域(Mestayer et al.,2011;Hartog et al.,2013;张丽娜等,2020).研究表明,基于单个解调仪,并采用多个双向放大器,能够以0.25 m的道间距实现几千到几十千米范围内的地震动信号观测,这样的方式极大地降低了观测成本(Parker et al.,2014).另外,实验室测试结果表明方法的测量精度可达到纳米级应变,其频段完全覆盖常规地震勘探从0.01 Hz至49.5 kHz的频段(Parker et al.,2014).DAS技术从油气勘探地震领域获得成功应用(Mestayer et al.,2011)后不久,便被推广应用到天然地震学(Lindsey et al.,2017;Willis et al.,2017)、浅地表结构成像(Dou et al.,2017;Zeng et al.,2017)、物性变化监测(Mateeva et al.,2017)等领域.
浅地表结构面波成像领域,Lancelle(2016)基于美国威斯康星大学麦迪逊分校研究组在美国加州Garner Valley强地面观测站布设的762 m光缆采集的主动源地震信号,根据多道面波方法得到由扫频震源产生的2~10 Hz的面波频散曲线,并反演获得了100 m以浅的横波速度剖面.同样,Song等(2019)也做了类似的观测实验,利用分布式声波传感技术获得主动源面波频散信息,并成功用于浅地表横波速度成像.与之同步开展的是在浅地表横波速度成像上的热点研究技术之一的被动源面波方法的数据观测实验,基于DAS技术,Zeng等(2017)利用观测到的连续噪声记录成功实现了背景噪声面波成像工作,并将所提取的频散曲线结果与加速度计和主动源面波结果及前人研究结果对比,对观测技术及相应数据处理方法的可行性进行了验证.
有关分布式光纤声波传感技术在地震学、勘探地震、浅地表地下结构成像、岩石圈和地球内部结构成像、地震监测等领域的应用情况,张丽娜等(2020)进行了较为详细的调研和分析.虽然,目前国内的相关研究工作尚处于起步阶段,但借鉴国外已有的成功经验,国内的相关研究工作进展极为迅速.与观测技术配套的仪器设备也相继被研发并投入使用,取得了可喜的成绩(Yu et al.,2016;Chen et al.,2019).中国科学院精密测量科学与技术创新研究院曾祥方研究员团队于2018年7月在白家疃北京国家地球观象台,采用国产DAS设备开展了相关实验.他们采用落锤作为主动震源,利用普通通信光缆作为传感器开展了基于光纤声波传感技术的地震波场高密度观测试验,利用多道面波分析方法提取了可靠的瑞利面波相速度频散曲线,并反演获得了光缆下方浅层30 m以浅的二维S波速度剖面(宋政宏等,2020).同时,该团队还利用480 m埋地光缆记录了13小时的背景噪声记录,通过噪声互相关方法得到相应的虚震源面波记录,同样采用多道面波分析方法获得了被动源面波信号的频散曲线,反演后获得了相应的研究区内二维横波速度剖面(林融冰等,2020).通过将主被动源分别提取的频散曲线提取结果及最终的反演结果进行对比,显示出分布式光纤声波传感器获得的观测记录具有较高的精度以及可靠性,同时检验了国产DAS观测设备的应用效果与观测精度(林融冰等,2020;宋政宏等,2020).Song等(2021a)给出了云南宾川县城市光缆下方的横波速度结构.与其他传统面波信号采集方式一样,DAS方法开展面波成像工作,也同样面临着因仅利用单分量记录所带来的瑞利波和勒夫波分离困难的问题.为此,Song等(2021b)发展了一种频散谱反演的方法,较好地克服了这一问题.
与陆地浅地表结构成像研究工作相比,由于海洋环境中固定地震台站(OBS)太过稀缺,以至于海底浅地表结构成像工作受到了极大地限制,一直以来进展缓慢.但随着DAS技术的提出,这一工作也迎来了新的发展.Cheng等(2021a)基于加利福尼亚州蒙特利湾近海20 km光缆上记录的环境噪声DAS记录,利用干涉测量技术从中成功提取到Scholte波的频散信息,反演成像了海底浅表沉积物的2D高分辨率横波速度图像,清晰刻画出了蒙特利湾浅海断裂带和古河道沉积构造.这一研究成果为海洋浅地表结构成像及海底通信光缆在地球物理上的应用指明了方向.
分布式光纤声波传感技术(DAS)因光纤材料廉价且分布广泛、观测便捷和具备海量数据传输能力等,在高密度和超高密度地震勘探数据采集上具有显著优势,特别是对在光纤网络分布密集的城镇区域开展高密度高精度浅地表结构成像工作具有广阔的应用前景.该观测技术目前已被科技部列入2021年度“变革性技术关键科学问题”重点研发专项,并已正式立项开展深入研究.
6 展望
面波成像技术发展至今,不管是主动源面波成像还是背景噪声面波成像技术在正反演理论、数据采集、处理与解释方法和配套软件开发等方面的发展已相对成熟.综上所述浅地表面波成像技术近年的研究进展情况,我们认为以下几个方面,依然是未来浅地表面波成像技术值得深入关注的研究方向:
(1)非完全弹性介质中的面波频散特性、衰减特性及其对勘探精度的影响研究.目前几乎所有的成熟方法与处理解释软件都是基于介质的完全弹性假设前提实现的,但完全弹性介质假设的理论对复杂的浅地表介质并不完全适用.而基于目前波动理论研究的成果,将浅地表面波成像技术的理论基础从弹性介质转变至黏弹性介质或孔弹性介质等,并不存在太大的困难.但关于黏弹性介质和孔弹性介质中的面波频散特性及面波在此类介质中的衰减等,对浅地表速度结构成像精度的影响尚缺系统性研究.如果需对介质中的衰减系数或品质因子进行反演,所采集的数据,除记录的相位信息外,振幅信息需要有足够的精度用于研究在介质中的吸收衰减过程.而浅地表介质的复杂性,又不可避免地会造成波的散射,这对数据采集技术和信号分析技术均提出了更苛刻的要求.另外,反演参数的增加,对反演技术来说也是一种挑战,其稳定性和反演精度等均易受到影响.以上原因,造成了实际资料面波成像应用中考虑吸收衰减因素的反演要远远落后于其理论研究.主动源面波勘探中虽已有部分成功的案例,但离其大规模运用还需继续深入研究.而地震背景噪声面波成像中考虑衰减的反演,目前主要集中在大尺度的地球内部结构研究,在高频背景噪声面波成像中考虑面波的衰减情况的研究尚较少见.另外,从背景噪声面波互相关函数的表达上,对于衰减介质而言该函数高度依赖于噪声源的分布,对背景噪声干涉的衰减成像还存在着较大争议.
(2)多分量面波频散特征及应用研究.如前所述,面波各分量在时间域与频率域等均存在一定的差异性与互补性,相对于传统的单分量反演而言,多分量信息可为反演过程提供更多的约束信息,使反演过程更合理、更稳定.多波多分量面波勘探方法在未来应成为浅地表面波成像技术的主流方法.多分量面波频散特征的深入研究,有助于寻求正确的模式识别方式和避免面波模式误判的问题,有利于更好地利用多模式面波进行联合反演,提高反演精度、增大反演深度、降低重建模型的不确定度.伴随着背景噪声面波成像技术的发展,多分量噪声观测与处理技术同样得到了长足的发展,除常规的利用噪声记录互相关提取瑞利波信息外,由多分量地震台站的切向分量中同样可以提取到有效的勒夫波信息,这使得利用背景噪声面波成像技术研究地球内部结构的速度各向异性情况成为可能,也为浅地表介质横波速度结构的高精度探测技术提供了突破的方向.另外,多分量台站所记录的面波旋转分量的频散特征及相应的频散曲线高精度提取技术也是值得深入研究的方向.
(3)复杂介质模型中的面波传播特性及面波干涉理论.背景噪声面波成像技术通过互相关方法恢复重建两点间的面波格林函数,这一理论与其前期发展出的微动空间自相关技术、统计声学技术,和后期发展出的地震干涉方法在本质上是相通的.前期的面波成像技术研究,特别是大尺度情况下,一般仅考虑单分量且仅提取基阶模式面波信息,这可基于一些简单的物理模型和假设前提依据标量波动干涉理论即可正确解释.而对于浅地表介质成像而言,所利用的一般是高频面波信息,由于面波的多模式多分量特性,仅采用简单的标量波动干涉理论,已不足以正确解释所有的噪声现象,因此有必要深入研究多模式面波的干涉理论,特别是复杂模型下的多模式面波干涉.这也是在考虑多模态面波反演和介质衰减性条件下,从背景噪声记录中提取多模式面波格林函数及正确的模式分离方法研究的关键.
(4)高效的三维面波波形反演方法及基于散射的三维面波反演方法.面波波形反演方法为浅地表横波速度结构的高精度成像提供了极为有效的实现手段,但受限于波场正演速度的限制,目前多数的实际资料应用都集中于二维剖面资料的成像上,虽已有部分真正意义上的三维面波波形反演的成功案例,但离大规模的三维面波波形反演方法的实际应用还有较大差距.如基于傅里叶神经算子的人工智能偏微分快速求解算法(Li Z Y et al.,2021)等的运用,或是突破现有三维面波波形反演局限性的有力工具.除此之外,根据面波的传播特性,面波波形反演工作的全面开展还需解决如下几方面的关键技术问题.一是震源子波的选择或影响消除,虽然该方面目前已有部分解决策略,但均存在不同程度的问题,因此震源子波的正确估计问题,依然是面波波形反演值得深入研究的问题.二是浅地表介质的黏弹性、孔弹性特征问题.浅地表介质往往具有黏弹性、孔弹性的特征,地震波在此类介质中衰减明显,特别是高频信息损失严重.基于弹性波波动方程的常规波形反演工作,不足以精细刻画浅地表介质速度结构.因此,黏弹性介质和孔弹性介质中面波波形反演的目标函数形式、品质因子估计方法等是有待深入研究的.三是浅地表三维复杂介质中的面波场高精度模拟.面波相比于体波有着低速和短波长的特征,因此数值模拟研究时,为精细表征浅地表介质中面波传播特征,往往需要对模型进行更加精细的网格剖分.高精度和稳定的三维复杂介质中面波场正演模拟技术是面波波形反演工作需要进一步深入研究的关键问题.
在地震背景噪声面波成像技术中,面波层析成像技术目前是获得浅地表三维横波速度结构的主要方法,但该三维成像方法是基于简单射线理论的,并未考虑实际三维介质中可能存在的散射体对面波的散射效应.若基于波动理论,开展真正的高精度三维面波成像工作,需要深入研究面波的散射理论,而不仅仅只限于对一些简单模型的理论和试验研究.
(5)随着数据采集技术的提高,快速处理海量数据是我们面临的一个挑战.机器深度学习不仅是迎接这一挑战的有效方法,而且还具有降低反演多解性的潜力.Dai等(2021)提出了一种深度学习模型(DCNet)来快速地提取频率—速度域中的多阶面波频散曲线.基于数据驱动通过大量真实和模拟的数据对模型进行训练,得到的DCNet模型提取的频散曲线精度,可以满足地质工程勘探快速提取大量面波频散曲线的要求.Hu J等(2020)和Luo等(2022)利用机器深度学习反演面波频散曲线快速获得横波速度构造.他们的研究显示利用机器深度学习反演面波频散曲线过程稳定,同时有可能降低反演的多解性.我们可以期待更多有关地球物理大数据的研究成果.
致谢
感谢特约主编及两位评审专家提出的修改完善建议,感谢编辑部的大力支持.
