地震学衰减层析成像进展

戴启立，闪 昊，孟 昆，包雪阳,2,3*

1 南方科技大学 地球与空间科学系，深圳 518055

2 南方海洋与工程广东省实验室（广州），广州 511458

3 广东省地球物理高精度成像技术重点实验室（南方科技大学），深圳 518055

0 引言

地震波的波速和衰减是描述地球介质物理属性的重要参数.仅根据纵横波速度模型推断地下介质的物理属性分布存在多解性.介质的流变性质、熔融以及挥发分含量对波速与衰减的影响并不相同.因此，在发展和完善地震波速度模型的同时，通过地震学衰减成像建立精细的三维地震波衰减模型，可减少模型解释的多解性，为准确估计地球内部的岩石组成、温度和流体熔体等重要物理属性分布提供更完善的地震学证据.地震波衰减成像已成为研究地球动力学机制与板块运动过程的重要途经，在震源解析、地震监测与风险灾害评估、油气勘探等领域也有重要意义.

0.1 地震学衰减成像的基本原理

地震波在地球内部传播过程中，地球介质的滞弹性（包括固体的黏弹性和含孔隙性、以及孔隙流体和熔体的黏性）将波传播的机械能转为内能，造成地震波能量不可逆耗散的现象，称为地震波衰减（Knopoff,1964）.为评价地震波衰减的强弱，引入品质因子Q以定量描述波在一个振动周期内能量衰减的大小：

式中E代表波的初始机械能，ΔE代表波振荡一个周期后损失的机械能，ω为角频率.Q值越大，振幅衰减越弱，反之亦然.当Q≫1时，设地震波的初始振幅为A0，由式（1）可推出波随时间变化的振幅为：

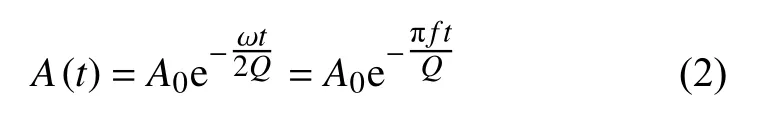
式中 ω和f分别为角频率和频率.通过提取地震波振幅信息即可根据式（2）测量品质因子Q.基于地震波射线理论，将式（2）改写为沿地震波传播路径的线积分：

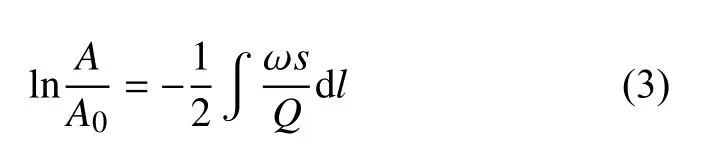
式中s和Q分别为线元 dl处的地震波慢度和品质因子.经典地震波衰减成像通常基于式（3）反演地球内部Q值的空间不均匀性.这在数学形式上和医学X射线断层成像（CT）是相同的.在地震学成像中，当考虑非均匀介质导致地震射线发生弯曲时，反演问题为非线性，通常可通过线性化迭代求解，例如利用射线追踪等算法计算每次迭代的核函数.前人在反演中常采用正则化以约束反演的稳定性，具体的求逆算法包括直接求逆、奇异值分解、代数重建和最小二乘QR分解等.

除滞弹性衰减外，震源激发与辐射花样、仪器响应与场地效应、波传播过程中的几何扩散、聚焦散焦、散射等多种因素均可影响地震波振幅的强弱.因此，从地震波振幅中获取准确的衰减信息，需要排除这些因素的干扰.传统上将介质滞弹性造成的地震波振幅减弱称为固有衰减（intrinsic attenuation），而常将波传播过程中因聚焦散焦（对于相对长波长的地震波，Lay and Kanamori,1985;Woodhouse and Wong,1986）和散射（对于相对短波长的地震波，Aki and Chouet,1975;Sato and Fehler,1998）造成的地震波振幅变化统称为散射衰减（scattering attenuation）.散射衰减在完全弹性介质中仍可存在，其本质上并非机械能向内能的转化，而是机械能在时空中的重新分布.在利用地震学衰减模型解释地球介质物理属性时，通常更注重固有衰减的特征.

0.2 地震波衰减的物理机制

当地震波穿过浅层地下介质如沉积层和上地壳等脆性区域时，孔隙和裂纹中的滑动摩擦会产生静态滞后现象，导致地震波能量的滞弹性耗散（Walsh,1966;Jackson and Anderson,1970），这一机制受流体含量、孔隙大小和裂缝密度控制.在活动断层附近，应力频繁的积累和释放将导致部分区域具有高裂缝密度，在海底断层中高裂缝密度区域将促进海水下渗（Kohli et al.,2021），导致地震波衰减增强.而在地球内部高温高压环境下传播的地震波，在剪应力作用下将使存在位错蠕变的矿物（如橄榄石）晶体发生受迫阻尼振动（如，Jackson and Anderson,1970;刘建华等,2004;Farla et al.,2012），或引起矿物晶体边界的滑动摩擦（如，Gribb and Cooper,1998;Jackson and Faul,2010;Jackson et al.,2014），使得地震波的能量发生滞弹性耗散.关于熔体喷射流模式在地震波频段范围内是否是一种独立的固有衰减机制仍存在争议（Mavko and Nur,1975;Hammond and Humphreys,2000a），已有研究指出其可以归结为受温度和压力影响的晶体边界滑动摩擦引起的应力松弛（Carcione et al.,2020）.静态滞后、阻尼振动以及滑动摩擦的本质是应力松弛，应力松弛所导致的应力-应变随时间变化的蠕变关系是产生地震波衰减的原因（Karato and Spetzler,1990）.

近年来逐渐丰富的高温高压岩石实验观测结果，为基于衰减成像模型定量分析深部地球介质的温度和黏度、熔融以及挥发分含量分布等提供了重要的实验数据支撑.通过引入实验室可测量的熔融温度Tm，品质因子Q与温度的关系可被表达为：

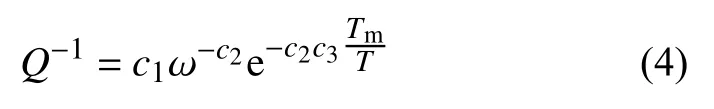
式中 ω为角频率，T为温度，c1、c2和c3为受岩石组分、晶体尺寸和挥发分物质等影响的参数（修改自Sato et al.,1989;Karato,1993）.根据式（4）可通过测量Q值约束地下介质的温度结构（McCarthy et al.,2011;Takei et al.,2011,2014;Priestley and McKenzie,2013;Yamauchi and Takei,2020;Adam et al.,2021）.地幔中的矿物颗粒尺寸也会影响岩石的滞弹性，颗粒增大可能减弱晶体边界滑动，从而降低衰减（Faul and Jackson,2005;Jackson et al.,2014;Dannberg et al.,2017）.上地幔的衰减还被认为与部分熔融有关（Hammond and Humphreys,2000a,2000b;Faul et al.,2004;Kumar et al.,2020;Havlin et al.,2021;Lyakhovsky et al.,2021），微量的熔体存在或是在预熔（premelting）的环境下衰减呈现显著增加的特征（Yamauchi and Takei,2016,2020）.高温高压实验表明填充于名义无水矿物点缺陷内的水也会明显增强衰减，但并不直接影响波速（Karato and Jung,1998;Karato,2003）.关于岩石组分，岩石力学实验发现橄榄石镁指数对衰减的影响远低于其对波速的影响（如，Faul and Jackson,2005）.

0.3 地震波衰减成像的研究意义与研究现状概述

基于地球自由振荡和面波数据建立的全球一维Q值模型（如，Dziewonski and Anderson,1981;Widmer et al.,1991;Durek and Ekström,1996）是认识地球内部介质滞弹性属性的基础.这些模型的主要特征可以总结为：在岩石圈中，S波Q值低于P波Q值；在软流圈中，Q值与波速的变化呈正相关，即高Q值往往对应高波速，反之亦然；在200 km以下的深度范围，Q值随着深度增加而逐渐增高，并在经过地幔转换带后显著增高；下地幔的平均Q值高于上地幔.但是，不同的一维Q值模型之间仍存在不可忽略的差异，在地壳和深部地幔尤为显著，这可能是由于地球内部Q值分布不均匀以及不同研究采用的数据不同所致（Resovsky et al.,2005）.建立精细的三维Q值模型将为解决这些争议以及进一步提高地球内部的认识提供参考依据（Savage et al.,2010）.

近年来三维地震波衰减成像结果为认识全球和区域尺度的壳幔动力学过程发挥了重要作用，如上地幔部分熔融特征和板块运动的驱动力（Debayle et al.,2020）、俯冲带地幔楔的形成机制和过程（Abers et al.,2014;Wei and Wiens,2018,2020;Zhao,2021）、俯冲带大地震的触发机制（Nakajima and Uchida,2018）、洋中脊和热点下方部分熔融的分布特征（Adenis et al.,2017a;Eilon and Abers,2017）、地壳流的空间分布（如，Dai et al.,2020）、地壳中裂隙的存在与闭合状态（Magrini et al.,2021）等.精细的衰减模型有助于从地震波形数据中准确反演震源机制以及监测核爆等（如，Gallegos and Xie,2020）.此外，地震波衰减成像结果也有助于正确解释速度模型.由于波速受地球介质滞弹性影响产生物理频散（Liu et al.,1976;Kanamori and Anderson,1977），即不同频率的地震波传播速度不同，因此在比较不同的速度结构时，需要根据Q值模型将速度模型换算到相同参考频率下进行比较.

尽管Q值模型的建立对于理解地球介质属性、动力学过程与震源机制等研究提供了新的约束，但现今三维Q值建模仍在减少测量误差、提高模型分辨率和减小不确定性上面临着挑战.地震学上的衰减测量一般依据地震波的时间序列振幅或频率振幅谱，但由于地震波振幅普遍受到震源性质和地球介质弹性非均匀性等因素的影响，导致固有衰减的测量和建模相比于波速的测量和反演而言，呈现出精度更低、误差更大的特征.从地震波振幅中获取衰减信息的困难主要体现在由速度结构不均匀导致的聚焦散焦效应等因素的影响不易准确估计、仪器响应记录的不准确性导致记录的振幅信息没有相位信息精准、以及估计震源机制解时引入的测量和计算误差等.面波衰减成像的单台法、双台法等传统方法常忽略了聚焦散焦效应，然而依据面波射线理论（Tromp,1994;Wang and Dahlen,1994;Larson et al.,1998），准确定量估计聚焦散焦效应对面波振幅的影响已被认为是面波衰减成像中不可忽略的步骤（Dalton and Ekström,2006）.体波和区域震相等衰减成像对波形相关的先验或后验信息利用有限，在一定程度上影响到对测量误差和模型不确定度的准确估计.值得指出的是，传统的地震衰减成像的反演架构大都是基于地震波传播的大圆或弯曲射线理论，而近年发展迅速的全波形成像基于有限频理论，在理论上具有一定的先进性.受到计算资源的制约，目前全波形衰减成像仍处于发展阶段且远未普及.

1 面波衰减成像

1.1 面波射线理论中的振幅

从面波振幅中获取衰减信息是建立全球衰减模型的重要方法.基于面波射线（JWKB）理论（Tromp and Dahlen,1992a,1992b;Tromp,1994;Wang and Dahlen,1994;Larson et al.,1998），面波传播的位移场在频率域的表示为（Wang and Dahlen,1994;Larson et al.,1998）：

式中振幅A和 相位ψ 分别为：

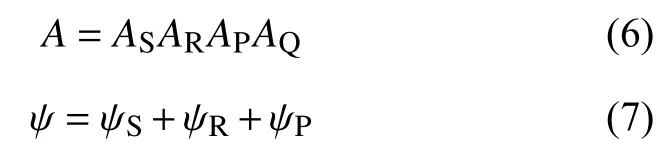
式（6）与式（7）中各项的具体表示为：

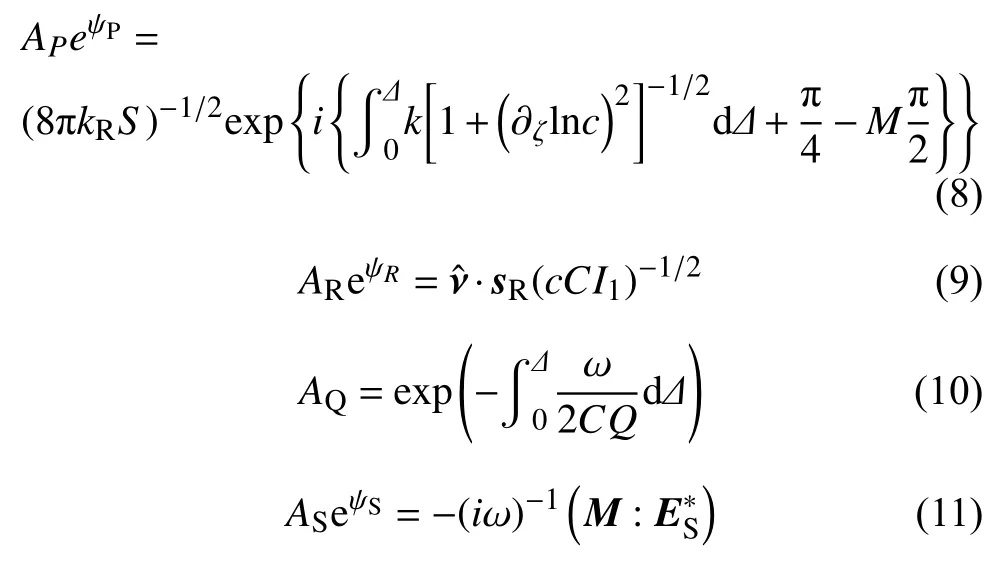
式（8）表示几何扩散和聚焦散焦效应（详见1.2节），AP和 ψP代表该效应对振幅和相位的影响，下同.式（9）表示仪器响应和场地效应，单位向量νˆ 代表仪器极性方向（polarization direction），sR代表面波在台站处的特征向量，(cCI1)-1/2代表场地效应，c和C分别为相速度和群速度，I1为密度和本征函数在深度r上的积分（Tromp and Dahlen,1992b）.场地效应是指由于台站下方存在着波速显著变化的特征，导致台站记录的地震波振幅发生放大或缩小的现象.式（10）表示沿面波传播路径的衰减，Δ为弧度表示的震中距.式（11）表示震源激发和辐射花样，其中M代表地震矩张量，ES代表震源处的应变张量.更多的细节参考Tromp和Dahlen（1992b）与Larson等（1998）.在全球面波衰减成像工作中，往往先根据已解出的震源参数和速度模型计算出理论地震波形，再通过测量实际地震波振幅相对理论地震波振幅的扰动进一步反演Q值模型（详见1.3节）.

1.2 聚焦散焦效应

当地球介质的速度结构存在横向非均匀性时，地震波会发生聚焦和散焦，这种效应主要受垂直于传播方向的相速度梯度影响.聚焦散焦效应导致面波振幅对弹性非均匀体的几何形态、尺度、以及波的传播路径敏感.因此，准确地定量估计聚焦散焦效应在面波衰减成像研究中至关重要（Bukchin et al.,2006;Dalton and Ekström,2006;Dalton et al.,2008）.估计聚焦散焦效应（包含几何扩散）的主要方法包括大圆路径近似法、射线弯曲法和面波射线有限频法（如，Dalton et al.,2013）.

大圆路径近似法假设地震波沿大圆路径传播，此时聚焦散焦效应可近似为（Woodhouse and Wong,1986）：

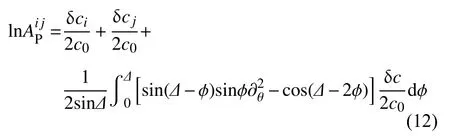
式中i和j分别代表事件和台站，Δ、θ和 ϕ分别为震中距、沿大圆路径的坐标和垂直于大圆路径的坐标（若考虑地震位于北极点，则 θ为余纬度，ϕ为经度），代表面波相速度的扰动.

射线弯曲法是通过求解动力学射线追踪问题得到与聚焦散焦效应有关的振幅信息（Larson et al.,1998）：

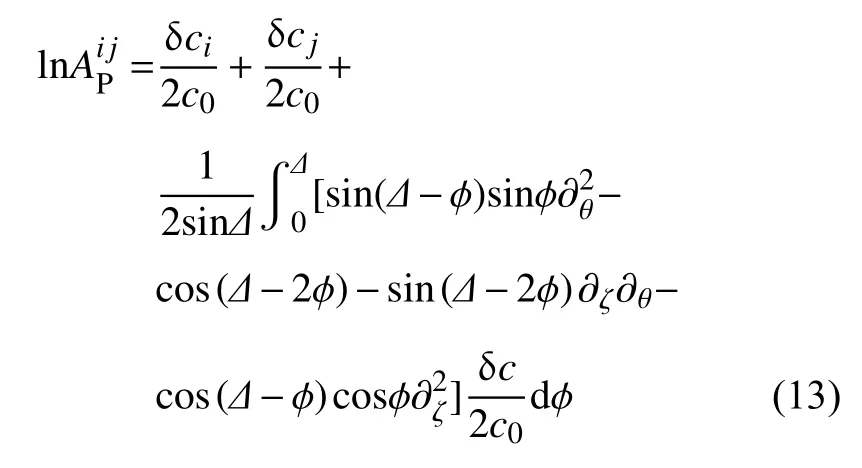
对比式（12）与（13），与大圆路径近似法不同的是，射线弯曲法添加了两项与波矢量方向 ζ有关的项.

对于面波射线有限频法，聚焦散焦效应导致的振幅扰动信息可以由速度扰动在单位体积 Ω上的积分表示：

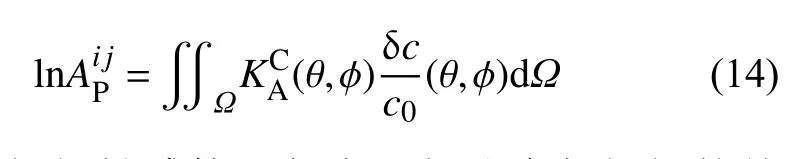
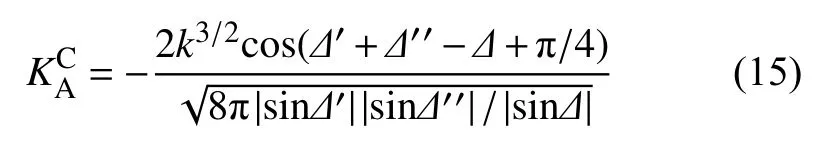
式中k是单位体积内的波数，Δ′、Δ′′和Δ 分别是震源到散射体、散射体到台站以及震源到台站沿大圆路径的弧度.式（15）假设散射体受震源和台站因素的影响一致.

Dalton等（2013）与Bao等（2016b）对比了以上三种计算方法得到的聚焦散焦效应的异同点及其对衰减模型的影响.大圆路径近似法与面波射线有限频法计算的振幅异常呈线性相关，而射线弯曲法与以上两种方法的线性相关程度较低，这说明该方法中射线穿过的路径与另两种方法存在差异.在相对短周期（50 s）的结果中，面波射线有限频法计算的振幅相对较大，该现象在长周期（150 s）的结果中有所减弱.研究还观察到球谐函数的不同角度阶数同样对结果产生影响，面波射线有限频法在不同阶数下均能保持较为一致的结果，而大圆路径近似法和射线弯曲法受速度结构横向非均匀性的影响更大，导致不同阶数的计算结果差异较大.

1.3 全球面波衰减成像

面波衰减导致振幅扰动的球谐函数展开式为：

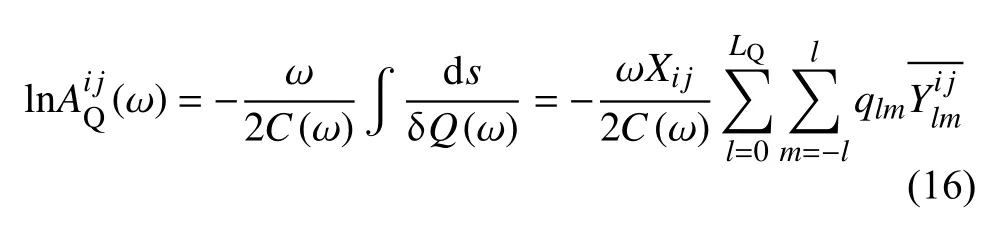
式中C和 δQ分别是面波群速度和品质因子的扰动，l和m分 别是角度阶数和方位角阶数，LQ是最大角度阶数，Xij是震中距，q是与衰减相关的待定系数，是沿着传播路径的球谐函数（Dalton and Ekström,2006）.结合已知的聚焦散焦效应和仪器响应，式（6）可以转化为：

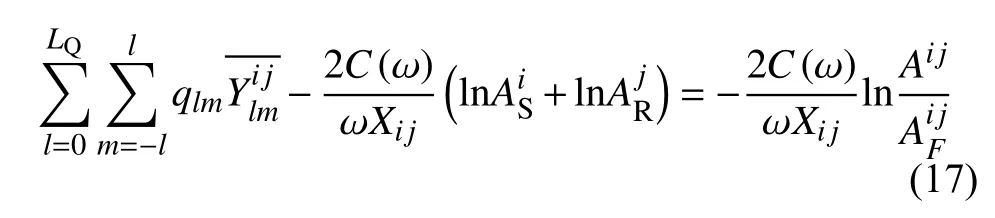
通过式（17）可以反演得到与衰减相关的待定系数qlm，并根据式（16）可以进一步计算出全球面波衰减模型（Dalton et al.,2008）.在求解过程中将场地效应扰动的总和归零以降低解的非唯一性，即令

前人已根据瑞利面波数据构建了不同周期的全球面波衰减模型（Romanowicz,1990,1995;Gung and Romanowicz,2004;Dalton and Ekström,2006;Dalton et al.,2008;Debayle and Ricard,2012;Bao et al.,2016b;Ma et al.,2016;Adenis et al.,2017a）.短周期的模型展示出地壳和上地幔中的Q值分布与板块构造特征之间存在相关性，长周期的模型则展示了地幔过渡带及更深部的衰减结构（如，Dalton and Ekström,2006;Dalton et al.,2008;Bao et al.,2016b）.地壳和上地幔中的低Q值异常主要分布在东太平洋隆起地区、北美洲西部和海底扩张中心（如洋中脊）.尽管大洋下方的Q值整体呈现随洋壳年龄的增加而增加的特征，但在太平洋西部地区一些洋壳较老的区域仍存在显著的低Q值异常，这被认为与热点及其下方的地幔柱有关（Adenis et al.,2017b）.地壳和上地幔中的高Q值异常主要存在于稳定的大陆克拉通内部，例如欧洲北部、澳大利亚西部、北美中北部、非洲和南美洲中东部（Dalton and Ekström,2006;Bao et al.,2016b;Dalton et al.,2017）.在地幔转换带深度下，Dalton等（2008）发现西太平洋的大多数俯冲带Q值相对较高，而低Q值异常主要分布在东南太平洋和非洲东部地区.

受数据覆盖、振幅测量误差、聚焦散焦效应的估计精度等因素的影响（Ringler et al.,2021），与全球波速模型相比（Ekström,2011;Ritsema et al.2011），全球衰减模型的分辨率仍然较低（Adenis et al.,2017a），在软流圈以下不同衰减模型的差异尤为明显（Karaoğlu and Romanowicz,2018b），体现出这些模型在分辨率和不确定性上仍有不足.随着密集台阵技术的发展和日益广泛的应用，区域尺度的面波衰减成像将为提高衰减模型的分辨率提供重要帮助.

1.4 面波亥姆霍兹成像

面波亥姆霍兹成像技术借助密集台阵观测数据，可以减少反演中对正则化参数的依赖，在近年得到快速发展（Lin and Ritzwoller,2011;Lin et al.,2012;Jin and Gaherty,2015;Bao et al.,2016a;Bowden et al.,2017;Hu et al.,2021）.基于横向弱非均匀介质假设，单一频率和振型的二维面波势函数 χ2D近似满足滞弹性介质中的波动方程：

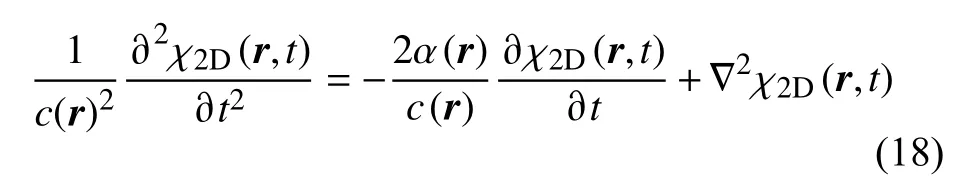
式中c为相速度，r为二维表面上的位置，α为衰减系数，与Q值的关系为 α=ω/2CQ，其中C为群速度.瑞利波的位移场uR可表示为 χ2D与场地效应因子β的积（Lin et al.,2012）：

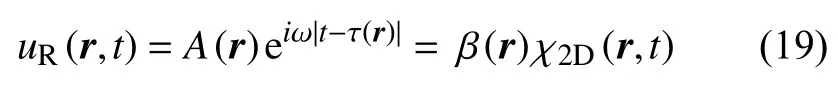
式中A和 τ为 频率 ω下的观测振幅和相位走时.场地效应因子 β的表达式为：

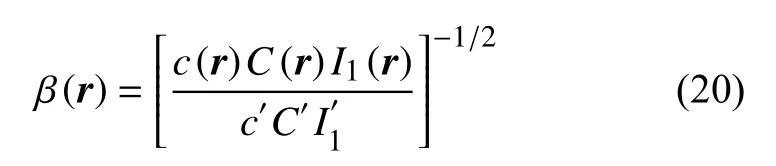
式中c′，C′和代表初始位置（震源）的参数.将式（19）代入式（18），其实部与虚部分别为：

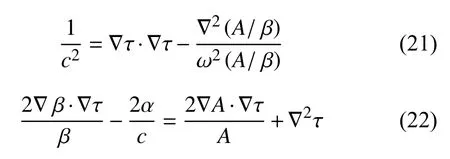
因此，先根据式（21）对面波在密集阵列中的相位和振幅进行二维插值和矢量运算获得相速度分布，再根据式（22）即可计算出衰减系数和场地效应，这一方法在本质上计入了波前愈合等有限频效应.Bao等（2016a）比较了三种求取衰减系数的方法：曲线拟合法、方位角平均法以及预估场地效应法（Eddy and Ekström,2014），证明不同方法得到的衰减系数较为一致，认为得到的衰减模型是可靠的.

Lin等（2012）根据周期为30 s和60 s的瑞利波信号获取了美国的衰减结构，揭示出美国东西部衰减结构存在鲜明差异.其中，地质构造活动更为频繁的西部地区具有显著的低Q值特征，而相对稳定的美国东部克拉通地区则呈现出高Q值的特征.30 s周期的结果对上地幔以及地壳结构更加敏感，如在高熔岩平原（High Lava Plains）、蛇河平原（Snake River Plain）和黄石（Yellowstone）等构造活跃区域衰减最强.60 s周期的结果与全球衰减模型较为一致，在科罗拉多高原和太平洋海岸附近地区呈现出低Q值特征.Bao等（2016a）利用亥姆霍兹成像计算了美国地区更宽频带（25～100 s）的衰减结构，并讨论了聚焦散焦效应对式（22）的影响，结果表明尽管局部区域可能无法准确地估算聚焦散焦效应，不同的方法在主要衰减特征中仍然呈现出较好的一致性.Bowden等（2015,2017）证明通过背景噪声干涉测量的振幅同样可以用于亥姆霍兹成像以计算衰减模型.

尽管亥姆霍兹成像在高分辨率面波相速度、衰减和场地效应建模上已取得了一些成果，但由速度非均匀性引起的聚焦散焦效应[由式（22）中走时场拉普拉斯项 ∇2τ所表示]对这一方法在衰减建模中的精度有很大程度的影响.当聚焦散焦效应对振幅的贡献大于衰减时（如面波传过沉积盆地时，Feng and Ritzwoller,2017），该影响尤为明显.如何提升式（22）的计算精度，减少因测量误差和不均匀插值造成的小尺度异常假象，是亥姆霍兹成像方法在高分辨率衰减成像中仍需解决的问题.

1.5 背景噪声衰减测量和成像

近20年来，利用背景噪声干涉提取经验格林函数的技术快速发展，该技术广泛应用于揭示地下速度结构（如，Shapiro and Campillo,2004;Shapiro et al.,2005;Bensen et al.,2007;Lin et al.,2008）.相较于地震面波信号，背景噪声干涉可以提取相对短周期且高信噪比的面波信号（Cupillard and Capdeville,2010;Rohrbach et al.,2013），从而建立高分辨率的速度模型（如，Gao and Shen,2014;Janiszewski et al.,2019;张智奇等,2020）.

Weaver（2011）指出从背景噪声干涉波形中提取振幅信息研究地震波衰减是可行的，但由于其中的振幅信息受到噪声源分布的影响，通过背景噪声提取衰减信息需要先确定噪声源的分布情况（Cupillard and Capdeville,2010;Tsai,2011;Weaver,2011;Stehly and Boué,2017）.Zhang和Yang（2013）提出根据噪声互相关尾波的互相关可以导出更为对称的经验格林函数，有助于提取更可靠的面波衰减信息.Weemstra等（2014,2015）认为常见的背景噪声数据处理技术（如谱白化、时间域归一化等）可能对振幅信息产生影响.为解决该问题，Boschi等（2019）根据互易定理提出了一种新的归一化准则，并通过数值模拟证明该方法在宽频带下（尤其是相对高频）仍然可以准确量化面波衰减（Magrini and Boschi,2021）.此外，Weaver和Yoritomo（2018）提出了时间域重加权（temporal reweighting）方法来解决常规技术导致的振幅信息不准确问题，该方法在实际应用中可以提取更可靠的振幅信息（Li et al.,2020）.Zhou等（2020）提出了非同步时间域扁平化（asynchronous temporal flattening）方法，该方法不需要所有台站在同一时间都记录数据，为建立更大面积的研究区提供了可能.

目前已有研究通过从背景噪声中提取的瑞利面波振幅与到时信息建立了局部及区域尺度的高分辨率衰减模型（如，Prieto et al.,2009;Lawrence and Prieto,2011;Lawrence et al.,2013;Bowden et al.,2015,2017;Liu et al.,2015;Toyokuni et al.,2021）.背景噪声和地震面波在相同周期下的结果有着较好的一致性，以美国地区周期为30～40 s结果为例（Bowden et al.,2017），盆岭省（Basin and Range）地区以及落基山脉的南部均呈现出低Q值的特征，而高Q值异常主要分布在美国大陆中部与东部.相较于使用远震面波构建的衰减模型，利用背景噪声成像可以获取更高频的信号以揭示地壳浅部以及沉积层的衰减特征（Bowden et al.,2015,2017;Allmark et al.,2018;Magrini and Boschi,2021;Magrini et al.,2021）.高频的衰减结构往往与地表的地质构造存在较强的关联性，如俄克拉何马州奥拉科根（Oklahoma Aulacogen）地区、北美中大陆裂谷（midcontinental rift）和格兰德河裂谷（Rio Grande rift）均呈现显著的高Q值异常（Bowden et al.,2017;Magrini et al.,2021）.

1.6 自由振荡

除通过面波振幅提取衰减信息，还可通过分析自由振荡中不同振型谐振峰值求取Q值（Kanamori and Anderson,1977;Roult and Clévédé,2000）.衰减不仅减弱自由振荡的振幅，还会增宽不同频率频谱的谱峰（栾威等，2021）.利用自由振荡，可以通过对比与修正理论地震图与观测地震波的谱峰差异测量每个振型的Q值，获取地幔和地核的衰减信息（如，Dziewonski and Gilbert,1971;Widmer et al.,1991;Talavera-Soza and Deuss,2020,2021）.

尽管通过面波振幅和自由振荡的方法计算全球Q值模型在理论上具有一致性，但前人有结果显示，在相同频率下根据面波振幅计算的Q值比自由振荡计算的结果高15%～20%（Dziewonski and Anderson,1981;Widmer et al.,1991;Durek and Ekström,1996）.Durek和Ekström（1997）认为噪声的存在可能会导致自由振荡的结果偏低，但Roult和Clévédé（2000）通过计算基阶和高阶振型以及加入噪声的影响，认为自由振荡的结果更加准确.

1.7 面波衰减成像对地球结构的新认识

通过结合全球和区域的速度和衰减模型以及岩石物理实验结果，一些研究对地幔中的温度结构、熔体或水含量进行了定量估计（Dalton et al.,2009;Ruan and Zhou,2010;Ruan et al.,2018;Ma et al.,2020）.

在海底下方150～200 km深度处，温度的横向变化范围大约在150 ℃～200 ℃以内；通过对晶粒大小的约束（d=1 cm），海底下方200 km的温度大约在1 370 ℃～1 550 ℃之间（Dalton et al.,2009）.大陆地区的温度结构相较于海洋地区更为复杂，地幔捕虏体的证据表明克拉通地区在100 km深度下的温度大约为900 ℃～1 000 ℃，150 km深度处的温度大约为1 100 ℃～1 200℃（Rudnick et al.,1998）.然而在岩石物理实验中，基于橄榄石的速度、衰减与温度间的关系，大陆地区150 km深度处的温度是小于1 000 ℃的（Dalton et al.,2009）.这可能是由于大陆岩石圈内岩石组分或含水量变化范围较大引起.尽管目前对大陆岩石圈温度结构还存在争议，但在相同深度范围下（如150～250 km），一般认可大陆地区的温度是低于海洋地区的，这被认为与岩石圈软流圈边界的深度分布有关（Dalton et al.,2017）.

热点、弧后盆地以及一些强构造活动地区（如青藏高原）下方100 km的熔体含量可能在0.3%以上，随着深度的增加，熔体含量整体呈现下降趋势（Debayle et al.,2020）.洋中脊地区的熔体含量在40～80 km深度处可达到1%以上（Yang et al.,2007;Ruan et al.,2018），但在200 km深度处下降至0.3%～0.7%（Debayle et al.,2020）.年轻海洋岩石圈的熔体含量相对较高，但古老海洋岩石圈下方的熔体含量较低，通常在0.1%以下（Debayle et al.,2020）.板块运动速度与熔体的含量呈正相关，这可能是熔体的存在减少了岩石圈和软流圈间的黏度，促进了解耦作用的产生（Debayle et al.,2020）.

由于水的存在可能使矿物晶体本身的性质发生改变（如与氢元素相关的缺陷），目前基于衰减实验估计地幔中水含量仍然存在争议（Ma et al.,2020）.Aizawa等（2007）基于橄榄石的实验推测在俯冲板片上方和热点下方的地幔中均具有较高的水含量，洋中脊下方100 km深处的水浓度可能在200 ppm以上（Ruan et al.,2018）.近期高温高压实验表明（Liu L et al.,2022），地幔柱的上涌岩石存在含水相，在上升过程中会释放水分，进而形成热点火山.然而也有研究者认为这些区域的高衰减本质上是由于氧化还原反应导致（Cline et al.,2018），结晶水对速度和衰减造成的影响是有限的（Debayle et al.,2020）.

2 体波衰减成像

2.1 体波t＊的测量

体波衰减成像通常基于射线理论并使用参数t*描述地震波在滞弹性介质中的衰减（Morozov,2013），先根据地震波速度记录的振幅谱A(f)拟合t*（Scherbaum,1990），再将t*表 示为Q值在地球内部沿射线路径的积分：

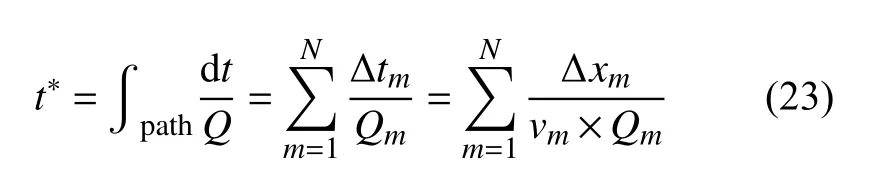
式中 Δtm、vm和Qm分 别代表射线经过第m段 路径Δxm的走时、速度和Q值，即可利用t*和 速度模型反演Q值模型.基于Brune（1970）对震源模型的假设，忽略场地效应和聚焦散焦效应，t*与A(f)的关系可表示为：

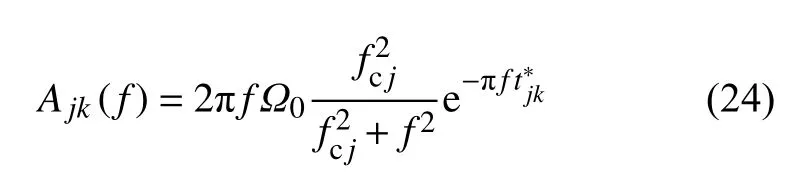
式中j、k、f和fc分别代表事件、台站、频率和拐角频率；Ω0代表低频下平均谱水平值，还被认为包含了几何扩散效应（Eberhart-Phillips,2016）.由于同一个地震事件的拐角频率是唯一的，可通过以下步骤计算（Eberhart-Phillips and Chadwick,2002）：先进行网格搜索寻取对应观测振幅谱Ojk(f)和理论振幅谱Ajk(f)残差最小值的拐角频率为该路径的拐角频率，然后将地震事件j每条路径上计算的拐角频率的均值设为该地震事件的拐角频率fc，再用非线性最小二乘法拟合速度振幅谱求取 Ω0和.虽然式（24）忽略了场地效应的影响，但也有研究认为可通过计算振幅谱的残差等方法拟合场地效应（Stachnik et al.,2004;Wei and Wiens,2018）.

对于近震体波衰减成像，结合当地精细的速度模型与式（23）即可通过线性反演解出衰减模型.对于远震体波衰减成像，常使用谱比法（Teng,1968）或时间域波形匹配法（Bezada,2017）计算Δt*探索研究区下方衰减特征.谱比法是将两个台站的速度谱[公式（24）]进行比较：

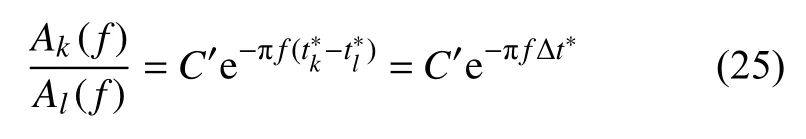
式中Ak(f)和Al(f)分别为两个台站的振幅谱，分别代表这两个速度振幅谱对应的t*，C′是一个代表不同台站差异的常数.通过该方法可以去除震源项和近震源衰减项，从而得到台站下方的 Δt*.与谱比法不同，波形匹配法是在时间域上对 Δt*进行拟合，因此考虑了衰减对相位造成的影响.根据Bezada（2017）提出的方法，公式（25）可改写为：

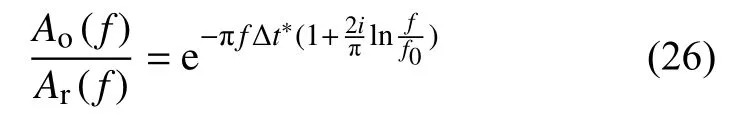
式中Ao(f)和Ar(f)分别为观测波形和参考波形的振幅谱，i为复数的虚部单位，f0是参考频率.时间域波形匹配法的步骤如下：先对同一事件在台阵数据中选取衰减最弱的波形作为参考波形，然后将参考波形通过式（26）对代表不同衰减的 Δt*进行网格搜索，计算波形振幅差的L2范数作为拟合残差，再选取使拟合残差最小的 Δt*作为搜索结果.利用谱比法或时间域波形匹配法拟合得到 Δt*后，即可根据式（23）计算出每个台站下方的Q值扰动.

值得指出的是，Liu等（1976）认为Q值在相对低频（0.001～0.1 Hz）范围内相对为一个常量，而在高频环境下强烈依赖于频率（Sipkin and Jordan,1979）.Lekić等（2009）表示Q值在相对低频范围下仍然存在一定程度的变化，但目前大多数面波衰减研究认为频率对Q值的影响十分有限，往往可以忽略不计.相较于面波而言，体波衰减成像通常使用相对高频的信号，这时Q值的频率依赖性是不可忽略的.在高频范围下，Q值与频率之间的关系可以近似为：

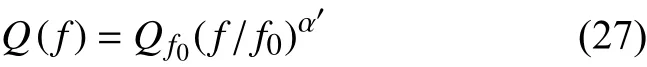
式中f0和分别是参考频率和在参考频率下的Q值，指数 α′与研究区的选择有关.大多数研究表明指数α′的范围大致为0.4～0.6（Boatwright and Seekins,2011;Eberhart-Phillips et al.,2016）.在体波衰减研究中，由于指数 α′与几何扩散存在折衷（Edwards et al.,2008;Eberhart-Phillips et al.,2014），因此如何准确地求取指数α′仍然是亟需解决的问题.

2.2 近震体波衰减成像

近震体波衰减成像的核心是根据衰减参数t*反演二维或三维Q值模型.由于t*代表了整条路径的衰减，反演Q值需先根据已知的速度模型计算射线穿过的路径（如利用射线追踪），再结合速度模型反演衰减模型[式（23）].

近震体波衰减成像为解析板块动力学机制和运动学过程提供了重要参考依据.日本地区的衰减结果显示低Q值区域与火山弧的分布具有良好的一致性（Wang and Zhao,2019;Zhao,2021;Zhao et al.,2021），板片俯冲地区呈现显著的高Q值特征（Abers et al.,2014,2020;Wang and Zhao,2019）.类似地，在南美洲和太平洋西南部的衰减研究中同样观察到俯冲板片的高Q值特征（Eberhart-Phillips et al.,2008;Jang et al.,2019），以及地幔楔与洋中脊地区具有低Q值的特征（Wei and Wiens,2018,2020;Jang et al.,2019）.美国加州地区的三维Q值模型揭示了低Q值可能与液体或熔融物质以及断层破碎带的分布有关（Lin,2014），而高Q值表明该地区可能存在低裂缝密度的火成岩基或低孔隙度的镁铁质岩石（Eberhart-Phillips et al.,2014,2016）.近震体波衰减成像也被应用于探索中国地区岩石圈的形变机制（如，马宏生等,2007;Pei and Chen,2010;孙莲等,2012;李金等,2017）.青藏高原中部地壳低Q值区域与共轭剪切带分布一致（Zhou et al.,2019），南部高Q值的岩石圈可能与俯冲的印度板块有关（Sheehan et al.,2014）.川滇地区的三维体波衰减模型与面波的结果较为一致（陈佳等,2012;Dai et al.,2020），指示了大火成岩省的壳内分布区域（苏有锦等,2006;周龙泉等,2009;Dai et al.,2020）并被用来推测青藏高原地壳流在东南缘的运移过程（Dai et al.,2020）.相比于青藏高原东南缘，在东北缘的衰减研究表明该地区可能并不存在地壳流（Liu and Pei,2021）.台湾地区的衰减研究通过Q值模型预测了台湾中央山脉的温度结构，对其造山过程提供了参考信息（Wang et al.,2010）.

2.3 远震体波衰减成像

远震体波衰减成像主要揭示台站下方地幔中的衰减信息（Bhattacharyya et al.,1996）.为得到高信噪比的波形记录以及减弱震源方向性效应，常选取震源深度在200 km以下的中强地震事件.谱比法已被广泛运用在研究岩石圈到地核的衰减结构中（Hwang et al.,2009,2011;Ichinose et al.,2014），为揭示俯冲带、热点、地幔不连续面的分布情况提供了参考依据（Allen et al.,1999;Eilon and Abers,2017;Farrell et al.,2017;Shrivastava et al.,2021;Soto Castaneda et al.,2021）.最近的一些研究利用时间域波形匹配法获得了欧洲与美国部分区域的远震体波衰减模型（Bezada,2017;Zhu et al.,2021），该方法被认为可以减弱散射和聚焦散焦效应对波形造成的影响.Bezada和Smale（2019）指出澳大利亚地区衰减结构的非均匀性由岩石圈地幔厚度或黏度的横向变化产生.Byrnes等（2019）获取了阿巴拉契亚山脉中部的远震衰减结构，推断该山脉下方可能缺失地幔岩石圈.Byrnes和Bazada（2020）根据美国南加州索尔顿海槽的衰减结构推测该地区早期洋壳的形成是由于大量地幔物质上涌导致.低Q值区域与火山活动的空间位置有较好的一致性，在中亚造山带、华北克拉通地区以及大兴安岭等地区的火山下方广泛分布低Q值异常（刘翰林和吴庆举,2021;Liu H et al.,2022）.Deng等（2021）利用远震体波衰减研究了华南地区岩石圈—软流圈系统的非均匀性，发现四川盆地岩石圈具有较厚和较强的岩石圈根，岩石圈厚度从四川盆地到华夏块体逐渐变薄.

2.4 地核体波衰减

基于自由振荡和体波的观测数据，液态外核的Qκ值被认为是趋于无穷的（Romanowicz and Mitchell,2008）.地球内核的衰减结构可以根据PKIKP和PKiKP震相的振幅比获取：一些研究利用谱比法计算两个震相的观测 Δt*，根据一维Q值模型（如IASP91）计算理论 Δt*，再通过拟合 Δt*反演Q值扰动（如，Ivan et al.,2006）；另一些研究通过正演不同Q值模型的理论波形，计算时间域下PKIKP和PKiKP的振幅比，并拟合观测震相的振幅比，从而推断内核的Q值模型（如，Wen and Niu,2002）.大多数体波研究表明，P波Q值在内核顶部相对较低，并且Q值随着深度增加而增加（如，Song and Helmberger,1993;Souriau and Roudil,1995;Cormier et al.,1998;Tseng et al.,2001），说明在内核浅部的介质黏度可能相对较高.然而，也有研究认为Q值在内核浅部几百千米范围内并不随深度而变化（如，Niazi and Johnson,1992;Bhattacharyya et al.,1993）.Wen和Niu（2002）发现东西半球内核的衰减结构并不均匀，这可能预示着内核内部存在热对流（Monnereau et al.,2010），Q值较低的东半球的熔融程度和温度相对较高，而西半球的高Q值意味着温度相对较低.此外，核幔边界在东西半球热通量存在差异也可能导致内核的衰减结构不均匀（Aubert et al.,2008）.Qin等（2019）、秦加岭等（2020）发现内核顶部衰减结构存在区域性变化，并认为内核的衰减存在各向异性的特征，推测是内核晶体定向排列的方式不同所致.

3 区域震相和尾波衰减成像

区域震相常被用于测量地壳和上地幔顶部的衰减结构，常见的区域震相包括Pn、Sn、Lg等，基于区域震相的振幅信息可利用单台法、双台法、逆双台法等估计其衰减结构（如，Chun et al.,1987;Xie and Mitchell,1990;Mitchell,1995;周连庆等,2008）.Pn和Sn波是主要在地幔顶部传播的高频地震波，被用于估计上地幔顶部的衰减结构（如，Yassminh et al.,2020），但其结果的可靠性受噪声和几何扩散的影响较大.T波是在海洋中传播的导波，其在大陆边缘产生的转换波已被用于约束地壳的衰减结构（Zhou et al.,2021）.Lg波主要在大陆地壳内传播，其信号往往是区域震相中最为显著的.Lg波的衰减被认为可以反应地壳中S波的衰减特征（如，Mitchell,1995），相关的衰减成像在大陆地壳区域已取得了不少结果（如，Romanowicz and Mitchell,2008;Bao et al.,2011a,2011b,2012;Zhao et al.,2013;Zhao and Mousavi,2018;赵连锋等,2018;Chen et al.,2021）.Lg尾波在短周期主要来源于S波在地壳内的散射，其振幅对聚焦散焦效应敏感度较低，可反映地壳内的平均衰减分布（如，Xie and Mitchell,1990;Mitchell et al.,2008;Romanowicz and Mitchell,2008）.最近的一项研究发现大地震产生的长周期尾波的振幅衰减受到深部地幔乃至地核的衰减性质影响，因此可有助于对全球一维Q值模型的改进（Jiang et al.,2021）.

4 全波形衰减成像

基于射线理论的衰减层析成像需要考虑非固有衰减因素对地震波振幅的贡献，如地球介质三维弹性非均匀性引起的聚焦散焦效应、场地效应和散射等.然而，受到射线理论中无限频假设的影响，这些效应难以通过射线理论精确计算.Ruan和Zhou（2012）提出固有衰减引起的滞弹性频散也可以导致聚焦散焦效应，暗示聚焦散焦效应的影响实际很难单独通过速度模型获取.此外，在实际测量地震波振幅过程中也很难精确提取特定震相的振幅信息（Bickel and Natarajan,1985），包括体波信号的时窗选取以及高阶面波对基阶面波信号的干扰等问题.

近年多项研究证明，基于三维参考模型的全波形成像考虑了三维非均匀地球介质对波场传播的精确影响，具有多参数自洽、精度和分辨率高的优点.在过去的十年间，得益于高性能计算机的飞速发展，全波形成像正逐渐成为反演多参数、高精度和高分辨率地球模型的重要方法.对于衰减建模，全波形成像利用地震波的全波形数据，不需单独计算聚焦散焦效应和场地效应对振幅的影响，计算敏感核时也不需确定所测量的地震波的具体震相，因此与传统衰减成像方法相比在理论上具有优势.

全波形成像通过求解非均匀介质波动方程，利用伴随成像（Tromp et al.,2005）或散射积分（Zhao et al.,2005）等方法计算全波形敏感核进而反演波速和密度等参数.全波形衰减成像的正问题基于广义麦克斯韦（Maxwell）体或齐纳（Zener）体波动方程，目前可利用谱元法或有限差分法，通过高性能计算实现三维波场正演模拟（如，Komatitsch and Tromp,2002;Moczo and Kristek,2005;Petersson and Sjögreen,2012;Wang et al.,2019），而反演问题则仍面临一些挑战.一是由于Q值最初是被转换为应力应变松弛时间存在于波动方程中的，当近似认为Q值与频率无关时很难通过反演直接估计松弛时间，不同参考频率下松弛时间的相关性也可能导致反演多解（Yang et al.,2020）.Fichtner和van Driel（2014）提出了一种Q值以显式参数存在于波动方程中的方法.Yang等（2020）也提出了一种新的反演框架用以同时反演速度与衰减模型.二是波速和Q值等参数在反演中的折衷问题.波形差异目标函数（如，Zhu et al.,2013）可能导致某个物理参数的误差对其它物理参数造成影响（Pan and Wang,2020）.例如过度地减小速度模型误差可能会增大Q值模型误差（Kamei and Pratt,2013;Fabien-Ouellet et al.,2017），而过度压制衰减的影响也会导致速度模型的不准确（Trinh et al.,2019），因此需要选取合适的目标函数以压制折衷问 题（Karaoğlu and Romanowicz,2018a;Pan and Wang,2020）.基于振幅的目标函数（如包络差异法）强调了衰减对速度的影响，被认为可以提供更可靠的Q值模型（Karaoğlu and Romanowicz,2018a,2018b）.

全波形成像技术的发展为精确创建地震波速度和衰减的多参数地球模型提供了条件（Li et al.,2017）.Zhu等（2013,2015）同时反演了欧洲大陆和北大西洋的上地幔速度与衰减模型，低Q值主要分布在洋底扩张中心和俯冲带的上方.该地区板块俯冲的深度达到了地幔转换带，并在地幔转换带中呈现出低Q值，这可能意味着板块俯冲携带了大量的水进入地球内部（Zhu et al.,2013）.与区域尺度的全波形衰减成像类似，全球尺度的全波形衰减模型在分辨率和精度上较传统面波衰减模型有所提升（Karaoğlu and Romanowicz,2018a,2018b）.模型显示250 km深度以上的高Q值主要分布在克拉通、大部分稳定的大陆和古老的洋壳地区，低Q值主要沿洋中脊和弧后地区分布（Karaoğlu and Romanowicz,2018b）；而在250 km深度以下大多数克拉通地区下方的高Q值逐渐消失，西南太平洋和东非地区可以观察到显著的低Q值（Karaoğlu and Romanowicz,2018b）.全波形反演也被尝试用于约束深部地幔的衰减结构（Borgeaud and Deschamps,2021）.

5 结论和展望

地震波衰减层析成像在精确建立地球模型、合理解释地球内部的物理属性、准确估计震源机制、提高地震勘探的精度等方面发挥着重要作用.在过去的十余年内，衰减层析成像研究取得了显著进展，其发展主要得益于以下因素：地震波传播理论对提高衰减信息提取精度的探索、层析成像反演方法上的开拓创新、以及海量地震观测数据的积累和高效计算资源的进步.但是，相比于地震波速层析成像在全球和区域不同尺度下均已取得的丰硕成果（如，Shapiro and Campillo,2004;Tape et al.,2007;Laske et al.,2013），衰减层析成像仍存在振幅数据误差较大、模型分辨率较低且不确定性较高等问题，这些问题是相关研究中需着重解决的难点.作为参考，笔者在此列举了地震学衰减成像理论和应用中一些正在开拓和发展的方向.

迄今大部分地震衰减层析成像都基于传统的线性最小二乘反演，此类方法需选取适当的平滑和阻尼因子以压制反演的多解性和不稳定性，但也可能导致模型的不确定性被严重低估（Resovsky et al.,2005）.在一些衰减成像研究中，对模型不确定性的定量评估几乎被忽略，这可能导致Q值模型被过度分析和解释.因此，基于数据的误差水平定量化估计模型的分辨率和方差，对判断Q值模型中异常特征的可信度起到关键性作用（Chen and Xie,2017;Ringler et al.,2021）.非线性贝叶斯—蒙特卡洛反演方法将观测数据不确定性作为独立待求解参数进行反演（Malinverno and Briggs,2004;Bodin et al.,2012a,2012b;Eilon et al.,2018），进而可以直接定量估计模型参数的不确定性（Byrnes et al.,2019;刘翰林和吴庆举,2021;Zhu et al.,2021）.随着反演算法的不断进步和计算资源的快速提升（如，Byrnes et al.,2019;Hu and Zheng,2020;蒋星达等,2022），贝叶斯反演方法在地震衰减成像中正逐渐展示其出色的效力和前景.

地球物理多参数模型联合解释已成为研究地球内部结构常用手段.速度与衰减结构的联合解释将为定量评价岩石圈和软流圈的温度结构、组成成分和熔体流体含量提供重要约束条件（如，Roth et al.,2000;Yang et al.,2007;Dalton et al.,2009;Martínez et al.,2010;Debayle et al.,2020）.与基于不同反演模型的多参数联合解释相比，多参数联合建模是相对更直接的研究策略.借助全波形成像技术在理论上的优势，重力与全波形联合反演已被用于同时提高速度模型与密度模型的精度和分辨率（Bao et al.,2021），在此基础上加入波形振幅信息进行衰减成像，可为研究地球内部的温度和流变结构提供新的约束.借助高性能计算的发展以及正反演技术的不断革新（如，Dutta and Schuster,2016;Leng et al.,2019;Wang et al.,2019;Romanowicz et al.,2020），全波形联合反演正成为揭示地球内部多尺度圈层结构的有力工具.

良好的数据覆盖是提升层析成像精度的主要途径之一.近年来，ChinArray和USArray等更多临时地震台网的布设，在区域尺度的层析成像中发挥了重要作用，显著改善了中国和北美地区的壳幔结构成像精度.未来需借助这些新数据，开拓新方法，以提高衰减成像的精度和三维分辨率，并拓展模型的覆盖深度.目前通过几十米或百米尺度间隔的地震台网研究地下小尺度结构和高频信息已取得显著成果（如，Wang et al.,2017;Gkogkas et al.,2021），但研究视角仍主要集中在基于体波和背景噪声的波速成像，衰减成像的成果相对不足（Meng et al.,2021）.随着密集台阵在地震学观测中的逐渐普及，衰减成像的视野也将有望向约束地壳内中小尺度异常的方向推进.观察大地震发生前后地下介质的速度和衰减变化情况正成为研究断层破裂趋势和流体渗透情况的重要途径（Nakajima and Uchida,2018;Wu et al.,2020;Lin and Shearer,2021;Guo and Thurber,2022），而高密度临时台阵为地下介质的时变观测提供了良好的基础.未来，在基于短周期地震仪台阵、分布式光纤阵列等新观测技术的地下结构研究中，加入高频的时变地震波衰减信息，可以为精确揭示地下介质多尺度时空分布提供重要约束.尽管现今在海洋和极地的地震波观测资料还有所欠缺，但随着洋底宽频带地震仪、海底光缆监测系统、以及更多极端环境下的新地震观测领域的开辟，地震学衰减层析成像必将在更广阔的研究领域中得到发展和应用.

致谢

感谢《地震学成像：方法与应用》专刊特约主编姚华建教授、特约副主编赵连锋研究员以及期刊编辑部等约稿.感谢梁晓峰和两位匿名审稿人的建设性的修改建议.感谢清华大学王念博士的宝贵意见.