考虑畸变影响的薄壁箱梁横向内力修正系数研究

2022-07-12何嘉祥张元海黄洪猛

铁道学报 2022年6期

何嘉祥，张元海，黄洪猛

(兰州交通大学土木工程学院, 甘肃兰州 730070)

现代桥梁设计中常用壁厚较薄、腹板间距和截面挖空率较大的箱梁。在竖向偏心荷载作用下，箱梁产生较大的横向内力,因此，设计过程中箱梁的横向配筋问题显得非常重要。箱梁设计中,工程设计人员往往更关注纵向内力分析而轻视横向内力分析，导致箱梁在投入使用后可能出现纵向开裂，严重影响桥梁的安全性和耐久性[1]。因此，开展箱梁横向内力分析很有必要。国内外研究人员对薄壁箱梁横向内力分析已有较多研究。文献[2-4]在双对称箱梁横向内力传统框架分析基础上，提出了带悬臂板的梯形箱梁横向内力计算方法。方志等[5]利用空间有限元软件对单室箱梁在轮压局部荷载作用下的横向内力进行了参数分析，提出了计算变截面箱梁横向内力有效分布宽度经验公式，分析了变截面箱梁横向受力分布规律。程翔云[6]采用有限条法计算箱梁横向弯矩并得到了顶板沿横向的弯矩包络图。汪洋生等[7]基于框架分析原理研究了箱梁横向内力，进行了参数影响分析，但计算得出的底板横向弯矩精度稍差。曾超等[8]在箱梁框架分析基础上提出了横向内力计算机分析方法。Kurian等[9-11]在对纯闭口混凝土箱梁进行三维有限元分析基础上，对比框架分析法提出横向内力的修正方法。钟新谷等[12]基于最小势能原理推导了箱梁横向框架效应单元刚度矩阵以及等效节点荷载。此外，文献[13-17]还研究了波形钢腹板组合箱梁的横向内力。

本文在刚性支承框架分析法基础上考虑箱梁畸变影响，推导单室薄壁箱梁的横向内力计算公式，采用“半框架模型”计算横向变位以提高横向内力计算精度，并研究横向内力修正系数以便工程应用。

1 横向内力修正系数及框架剪力差

工程中应用的箱梁属于空间薄壳结构，在偏心竖向分布荷载作用下，为分析箱梁的横向内力，往往沿梁长截取单位长度箱梁梁段，并在腹板下虚设支承，按刚性支承框架计算横向内力，但应考虑偏载下畸变效应引起的横向内力，对刚性支承框架内力进行修正。引入横向内力修正系数λ，其定义为

(1)

式中：m为考虑畸变效应后求得的实际横向内力(弯矩)；mR为仅由刚性支承框架求得的横向内力(弯矩)，可采用结构力学方法或杆系结构有限元方法求解。本文着重研究m的合理计算方法。

当箱梁沿桥跨纵向作用竖向偏心分布荷载时，可在箱梁底板两角点处虚设沿桥跨纵向连续分布的竖向刚性支承，在单侧腹板上下两角点处虚设沿桥跨纵向连续分布的水平刚性支承。通过对截取的单位长度梁段相应的横向框架进行分析，可得到上述4个角点处的反力。然而，由于上述刚性支承实际并不存在，需撤除这些刚性支承，即对箱梁在上述4个角点处施加与刚性支承反力大小相等且方向相反的力。这些反向施加的竖向反力可进一步分解为竖向对称荷载和反对称荷载，其中对称荷载作用下产生的横向弯矩可忽略不计。本文主要研究箱梁在竖向反对称荷载及水平反向荷载作用下的横向内力。

图1为截取的单位长度箱梁梁段框架尺寸及框架各杆所受荷载简图，其中，t′u、t′b、t′w分别表示框架上、下水平杆件及斜杆所受的扭转剪力差荷载，即截取的单位长度箱梁梁段在前后两个横截面处顶板、底板及腹板上扭转剪力流合力，撇号代表纵向坐标的导数。同样，T′u、T′b、T′w分别为相应的畸变剪力差荷载。框架除受上述剪力差荷载外，还有作用在相应角点位置处的竖向反对称荷载qv及水平反向荷载qs。

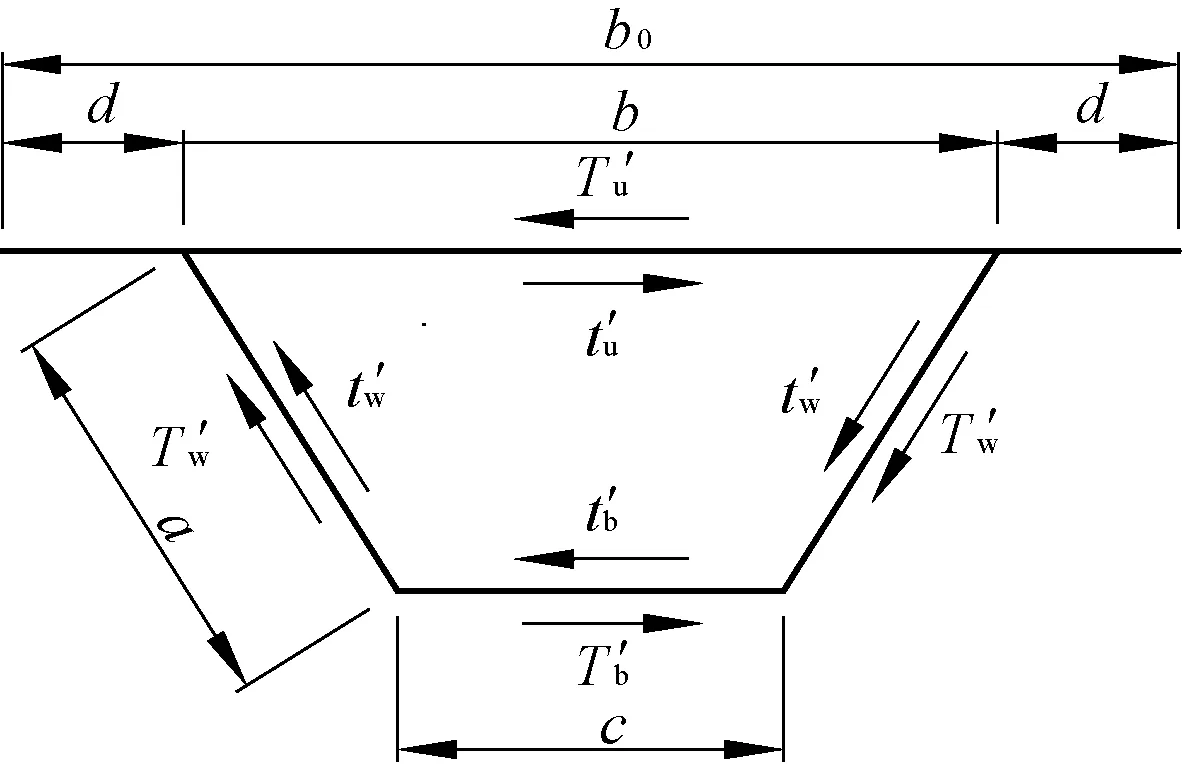
图1 框架尺寸及剪力差荷载

由腹板和底板交点处的扭转剪力流相等可知

(2)

根据箱梁在反对称荷载作用下的畸变分析理论可知，横截面上各板件畸变翘曲正应力及其对应的弯矩如图2所示。图2中，在角点A和D处的畸变翘曲正应力分别用σA和σD表示，上、下翼缘板及腹板的畸变翘曲应力在自身平面内的弯矩分别用Mu、Mb及Mw表示，它们都可通过σA表达。根据箱梁横截面上翘曲正应力不合成绕竖向对称轴的弯矩的平衡条件，可得畸变翘曲系数β为

图2 畸变翘曲正应力及板件弯矩

(3)

式中：β=σD/σA；α1=b0/b为上翼缘板全宽与顶板宽度之比；tu、tb、tw分别为箱梁上、下翼缘板及腹板厚度。

根据箱梁各板件弯矩与剪力之间的关系，畸变剪力差为

(4)

(5)

(6)

对比式(4)～式(6)可得，各畸变剪力差荷载之间的关系为

(7)

(8)

值得注意的是，在式(7)中，只有当α1=1，β=1，b=c，tu=tb时，即在双对称截面情况下，上、下翼缘板的畸变剪力差大小相等。对一般截面，箱梁上、下翼缘板的畸变剪力差并不相等。

2 框架变形分析及协调关系

如图3所示，框架在反对称荷载作用下，上、下杆的反弯点位于其中点处，剪力分别用Qu和Qb表达；腹杆处的反弯点将腹杆分成上下两段，其中上段腹杆长度为a/(1+ηm)，下段腹杆长度为aηm/(1+ηm)，ηm为仅取决于箱梁横截面尺寸的系数，腹杆反弯点处剪力为Qw。根据框架在各个角点处的弯矩平衡，可得

图3 框架剪力

(9)

(10)

对比式(9)与式(10)可知

(11)

因为箱梁框架结构具有左右对称性，其反弯点必位于顶板与底板的中点处，本文建立如图4所示的无侧移“半框架模型”。为求得对应于箱梁畸变的框架变形，在图4角点A处施加竖向力P，由竖向力平衡条件可得

图4 “半框架模型”简图

(12)

在小变形情况下，上述框架变形如图5所示，转角γ1和γ2可表示为

图5 框架变形

(13)

(14)

为了求解相对转角γ1和γ2，需求出框架的相对竖向位移ΔAy和ΔDy，按结构力学中的力法原理先求出框架内剪力，并作出荷载作用时的框架弯矩图，然后在A点作用竖向单位荷载并作出弯矩图，最后用结构力学方法求得用Qw表达的ΔAy和ΔDy为

(15)

式中：E为弹性模量；Iw为腹杆的截面惯性矩，Iw=tw3/[12(1-μ2)]；η1为与箱梁横截面尺寸有关的系数。

图6所示为箱梁横截面的畸变变形简图，畸变角与各板面内位移之间的关系为

图6 箱梁畸变变形简图

(16)

箱梁截面的畸变位移与各板件位移之间的关系为

(17)

式中：Jw=twa3/12；Ju=tub03/12；Jb=tbc3/12；α为取决于箱梁荷载形式和支承条件的系数。

由于框架取自箱梁，按框架所求的变形应该与箱梁畸变变形保持协调，对比图5和图6可知，变形协调关系为

γu+γw=γ1

(18)

γb+γw=γ2

(19)

联立式(13)～式(14)、式(16)～式(19)，并代入式(15)经整理可得框架腹板内剪力和畸变剪力差关系式为

(20)

3 框架内外力平衡关系

如图7所示，由内外力在水平方向和竖向的平衡及力矩的平衡关系，可建立如下平衡方程

图7 内外力的平衡

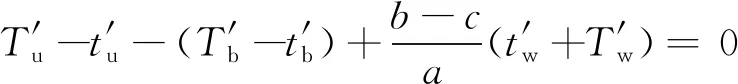
(21)

(22)

(23)

至此已建立了求解横向内力所需的全部方程，通过联立求解式(2)、式(7)、式(8)、式(10)、式(11)、式(20)～式(23)，求出框架剪力Qu、Qb、Qw后，即可求得考虑畸变影响的横向弯矩，再叠加刚性支承框架横向弯矩，即得最终的横向弯矩。

4 数值算例分析

4.1 理论验证与对比

以文献[3]中有机玻璃试验梁模型为例，梁的计算跨径为1.20 m，弹性模量为2 800 MPa，泊松比为0.37；竖向偏心均布荷载为1 kN/m，荷载作用点到顶板中心距离为60 mm。截面尺寸如图8所示。

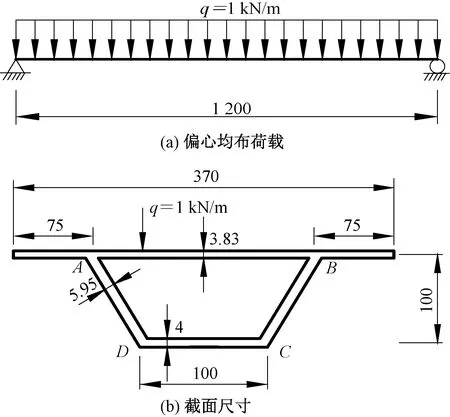
图8 荷载及箱梁横截面(单位: mm)

通过本文解析法和Ansys中Shell63单元计算跨中截面处顶板角点A和B以及底板角点C和D的横向弯矩(框架内侧受拉为正)，对比结果见表1。

表1 跨中截面角点横向弯矩对比

由表1可知，两种方法计算的角点横向弯矩与Ansys有限元计算值吻合良好。通过分析，C、D点的误差降到了3.3%和4.2%，相比文献[3]的计算方法，本文方法使点C、D的误差有所减小，点A的误差虽然略微增大，但其他角点的误差相对减小。这说明本文“半框架模型”横向内力计算方法能降低箱梁底板角点横向弯矩的误差。

表2为按本文方法和文献[3]方法计算跨中截面横向弯矩的相关截面特性参数。由表2可知，按两种方法求得的惯性矩和畸变翘曲系数相同，但η1和ηm值不同，这是由于取不同的框架模型而产生不同框架位移造成的。

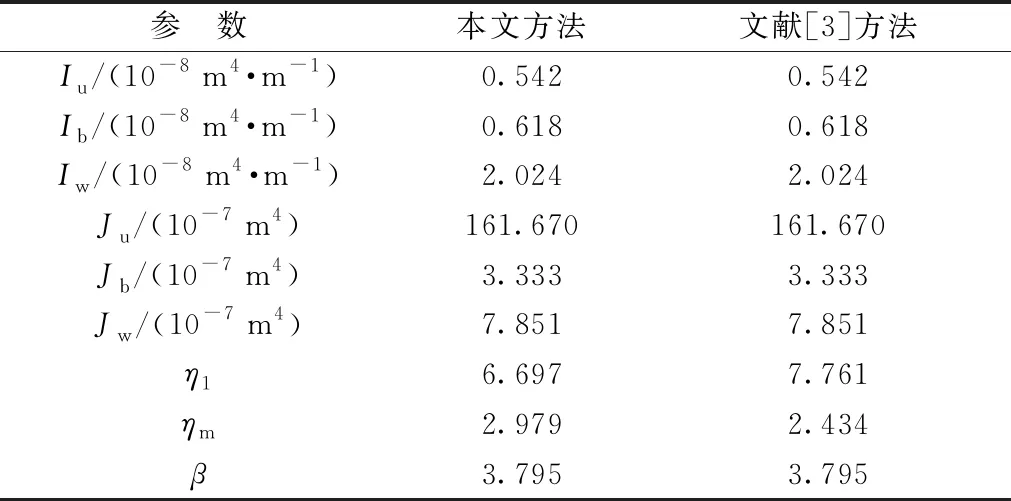
表2 截面特性参数

以跨径30 m单室混凝土简支箱梁为例[13]，梁上作用沿桥跨纵向的均布竖向偏心荷载为10 kN/m，偏心距为1 m。箱梁采用C50混凝土，弹性模量为34.5 GPa，泊松比为0.2，简化后的横截面尺寸如图9所示。

图9 箱梁横截面尺寸(单位: m)

分别用本文方法、刚性支承框架分析法及有限元Ansys 中Shell63单元计算跨中截面单宽横向弯矩，将三种方法所得结果绘于图10(框架内侧受拉为正)。

图10 跨中截面横向弯矩(单位：kN·m/m)

对比图10所示结果可知，本文改进方法计算跨中截面横向弯矩与Ansys计算值吻合良好，而按刚性支承框架分析法计算跨中截面底板处横向弯矩与本文改进方法计算得出的横向弯矩有较大偏差，甚至出现正负号的改变。由此说明，在竖向偏心荷载作用下计算跨中截面处横向弯矩时不能忽略由畸变产生的横向弯矩。

4.2 参数分析

为研究箱梁在偏心荷载作用位置变化时对跨中截面横向弯矩的影响，以图9中30 m简支箱梁截面为研究对象，在保持其截面尺寸不变的情况下，改变外荷载q的偏心距d，d的取值范围以0.5 m为步长从0增至2.5 m。根据对称性，只考虑荷载在左腹板与顶板的角点到顶板中点范围内的移动，暂不考虑荷载在悬臂板上的情况。

顶板上荷载作用点的横向弯矩为MF，由图11可以看出，跨中截面各点处的横向弯矩总体上有MF>MB>MA>MC>MD，顶板与左腹板角点A处横向弯矩值在荷载偏心距为0～0.5m范围内略微增大，而d>0.5m时MA迅速减小。荷载作用点弯矩值MF和角点B的弯矩值MB随着荷载偏心距的增大而逐渐减小，而底板与腹板角点弯矩值MC和MD近似于线性增长。

图11 跨中截面横向弯矩随荷载位置变化曲线

图12反映了跨中截面顶板角点A、B及荷载作用点F处横向弯矩修正系数λ随荷载偏心距d的变化规律。当偏心距d增大时，修正系数λB和λF均呈递增趋势，且λB的变化幅度更为明显，而修正系数λA逐渐减小。荷载偏心趋于很小时，顶板角点与荷载作用点处的横向弯矩修正系数λ趋近于1。

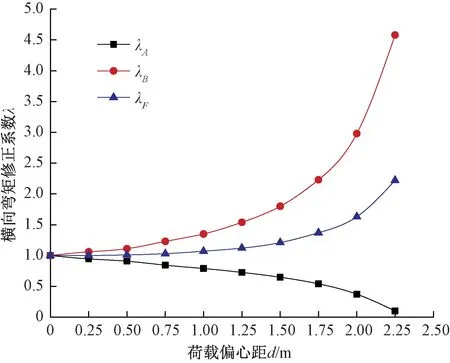
图12 修正系数随荷载偏心距变化曲线

图13反映了当箱室高宽比h/b=0.5时，顶板抗弯刚度和腹板抗弯刚度比(令抗弯刚度比k=Iu/Iw)对箱梁顶板处横向弯矩的影响。由图13可知，MF随着k的增大而增大，相应的MB在k值较小时呈现出平稳增大的趋势。当k>0.5时，MB缓慢减小，MA随着k的增大而迅速减小；当k约为0.25时，顶板两角点处的横向弯矩峰值最小。

图13 跨中截面横向弯矩随抗弯刚度之比k的变化曲线

图14反映了箱梁跨中截面顶板角点A、B及荷载作用点F处横向弯矩修正系数λ随抗弯刚度比k的变化规律。由图14可知，修正系数λA和λB的变化规律相反，随着k的增大，λA逐渐减小，而修正系数λB逐渐增大。此外，荷载作用点处的修正系数λF趋于稳定，约为1.06，即抗弯刚度比k的变化对荷载作用点处的修正系数影响较小。