桁架对列车气动特性的影响及其内部风场分析

郭薇薇，蔡保硕，张慧彬

(北京交通大学 土木建筑工程学院， 北京 100044)

近年来，为了适应现代社会对交通运输系统发展的需要，大跨度公铁两用斜拉桥得到了日益广泛的应用。由于桁架结构能较好地满足高速铁路和高速公路对结构刚度的要求，且具有透风性好、便于布置双层桥面等特点，成为公铁两用桥梁的首选主梁结构体系。例如，我国的天兴洲长江大桥、郑新黄河大桥、铜陵长江大桥和沪通长江大桥等，均采用了双层桥面布置的钢桁梁结构。

在强侧风作用下，当列车运行在桥梁上，车辆处于桥梁的气动绕流之中。桥梁的外形会影响列车的气动特性，而桥梁断面的气动特性也会随着列车行进发生改变[1]。已有不少学者针对车桥系统的气动特性问题，分别从试验和数值出发开展了一系列相关研究工作[1-12]。当气流通过桁架断面，不仅会在断面上、下两侧发生绕流，还有部分气流会直接穿过断面，这会影响运行其中的列车的三分力系数。文献[1-3]通过风洞试验，分别对横风作用下钢桁梁桥上的列车三分力系数进行了测试，其中王铭等[3]又进一步研究了列车进出桁架结构对列车三分力系数的影响。姚志勇等[4]通过数值模拟，对桁架内部车辆的三分力系数进行了分析，发现桁架腹杆的规则布置对车体会产生周期性的波动荷载。此外，还有少量文献通过风洞试验考察了桁架内部平均风速或随长度或随高度方向的变化规律[3,10]。这些研究可为本文提供理论和实验参考，但是系统完整地研究桁架结构对列车气动特性的具体影响及桁架内部风速场的空间分布还鲜见报道。

本文以新建的某公铁两用长江大桥为工程背景，首先采用风洞试验对比列车在桁架主桥和箱梁引桥上的三分力系数，然后根据总风压相等原则，对桁架内部等效风速及侧风折算系数的空间分布进行数值模拟，为综合评价列车在桁梁内部穿行时的气动特性以及合理确定车桥系统风荷载奠定基础。

1 试验模型及方案

试验在北京交通大学风洞实验室高速试验段中进行，该试验段尺寸为15 m(长)×3 m(宽)×2 m(高)。试验来流为均匀流，湍流度小于0.5%，风速为8～10 m/s，试验攻角α在-6°～6°之间变化。

某新建公铁两用长江大桥主桥采用跨度(140+462+1 092+462+140) m钢桁梁斜拉桥，南引桥采用70×48 m预应力混凝土简支箱梁桥。为了研究桁架结构对桥上列车气动特性的影响，分别制作了列车-桁梁和列车-箱梁两种缩尺节段模型，见图1。

图1 试验模型

综合考虑列车和桥梁的几何尺寸、风洞试验段的截面尺寸以及对阻塞率的要求，本文采用的模型几何缩尺比为1∶80。列车-桁梁模型的阻塞率为4.95%，列车-箱梁模型的阻塞率为1.21%。桁梁、箱梁的模型宽度与有效试验区高度的比值分别为0.219、0.076 5，两种模型长度与宽度的比值分别为5.99、16.99，符合JTG/T 3360-01—2018《公路桥梁抗风设计规范》[13]的要求。

桥梁模型采用不锈钢支架作为骨架，外壳采用ABS板材料制作。桥梁断面示意见图2。如图2所示，桁梁模型长为2 625 mm，宽为438 mm，高为223 mm，包含了15个桁架节间，考虑了挡砟墙和上层桥面下的U肋、横联等细部结构；箱梁模型长为2 600 mm，宽为153 mm，高为50 mm。

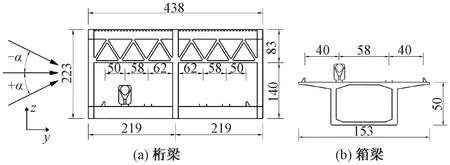
图2 桥梁断面示意(单位：mm)

列车模型以直达25 T列车为原型，采用1节车头+4节车厢共5节车辆编组的形式，见图3。列车模型采用ABS板材料制作，忽略门把手、车钩、转向架等细部结构，外形上与实物保持一致，以尽可能真实地模拟实际气流的绕流。本试验采用压力积分法计算作用在列车上的气动力。综合考虑测量结果的准确性、车辆模型的截面尺寸、模型内部的走线等情况，在头车和车厢1～3沿列车长度方向等间距布置3个测压面，间距为80 mm。每个测压面上布置了18个风压测点，共216个风压测点。

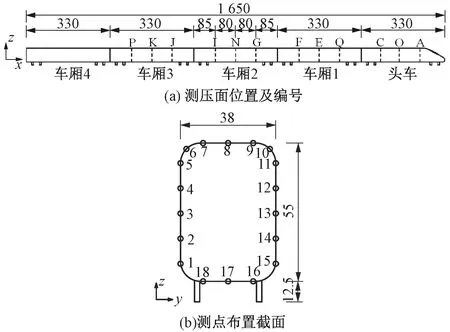
图3 列车模型及测压点布置(单位：mm)

桥梁模型的两端各通过一个5分力杆式测力天平与α攻角转盘相连，并通过电机驱动转盘来精确控制来流风与试验模型的夹角。通过螺栓将车辆模型固定在桥面，采用美国PSI公司的电子压力扫描阀测试车辆表面的风压。压力采集设备为4个ESP-64HD微型压力扫描模块，可实现256个点的高速同步测压。采样时长是80 s，采样频率为312.5 Hz。

2 试验数据处理及结果分析

2.1 数据处理方式

本次试验中，车辆模型和桥梁模型相接触。通过静力测试得到车桥系统整体的三分力，同时通过表面压强测试换算得到车辆的三分力，最后通过力的合成定理计算得到作用在桥梁上的三分力[8,14]。

在静力测试中，测力天平可以测出模型在横桥向y和竖桥向z的力及绕纵桥向x、横桥向y、竖桥向z三个坐标轴方向的力矩。风轴坐标系下的静力三分力系数可定义为

(1)

式中：CD(α)、CL(α)、CM(α)分别为风攻角为α时的阻力系数、升力系数和力矩系数；FD(α)、FL(α)、M(α)分别为风轴坐标系下的阻力、升力和力矩；ρ为空气密度，ρ=1.225 kg/m3；U为来流风速；h、w、l分别为节段模型的高度、宽度和长度。

将式(1)中的FD(α)和升力FL(α)分别换成体轴坐标系下的阻力FH(α)和升力FV(α)，即可得到体轴坐标系下的阻力系数CH(α)和升力系数CV(α)。两种坐标系下的力矩系数CM(α)相同。

在压强测试中，使用高灵敏度硅压阻传感器和气动连接器测量车辆的表面风压。作用在第i个测压点上的阻力、升力和力矩可以表示为压力和表面积的乘积[14]，即

(2)

式中：pi为第i个测压点测得的压强；dsi为相邻测压点之间的距离；di为第i测压点沿压强方向距车体形心的垂直距离；θi为第i个测压点压强方向与来流风的夹角。

2.2 不同梁型的三分力系数对比

箱梁和桁梁的静力三分力系数随风攻角的变化曲线见图4。由图4可知，当风攻角在-6°～6°范围内变化时，桁梁的阻力系数和力矩系数均显著低于箱梁。当风攻角为0°时，桁梁的阻力系数和力矩系数约为箱梁的42%、15%。当风攻角在-6°～4°范围内，桁梁的升力系数也低于箱梁，零攻角时桁梁的升力系数约为箱梁的11%，但当风攻角增至6°时，桁梁的升力系数较箱梁大50%。

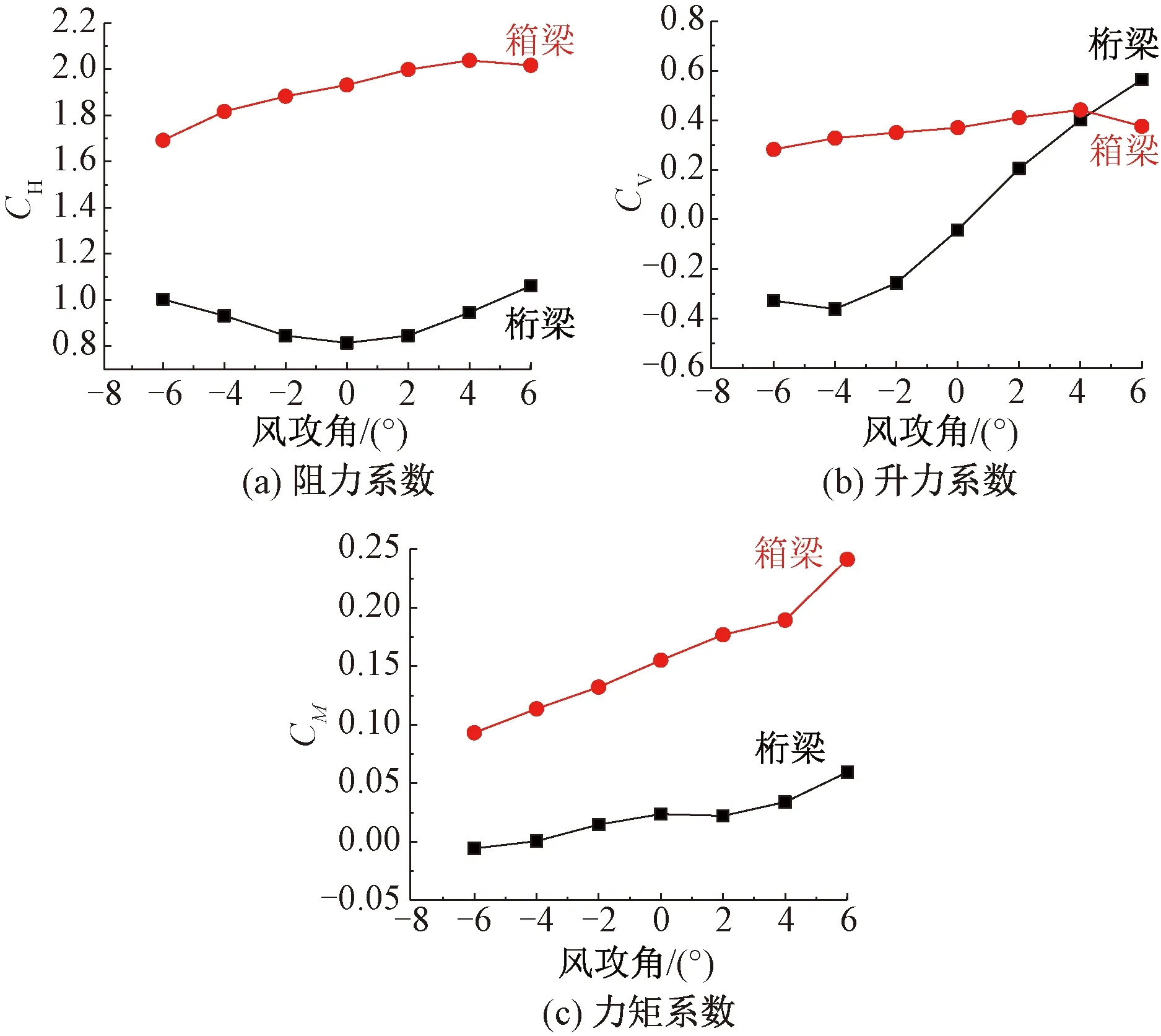
图4 两种梁型的三分力系数对比

2.3 车辆在不同梁型上的三分力系数对比

以车厢2为例，各测压面上的风压分布结果见图5，图5中测压面及测压点编号见图3。由图5可知，列车在桁梁上的表面风压较低，但由于车厢顶部受到桁架的遮挡，出现了一个波动较大的负压。车辆在桁梁和箱梁上的最大风压值分别为65.55、93.60 Pa。

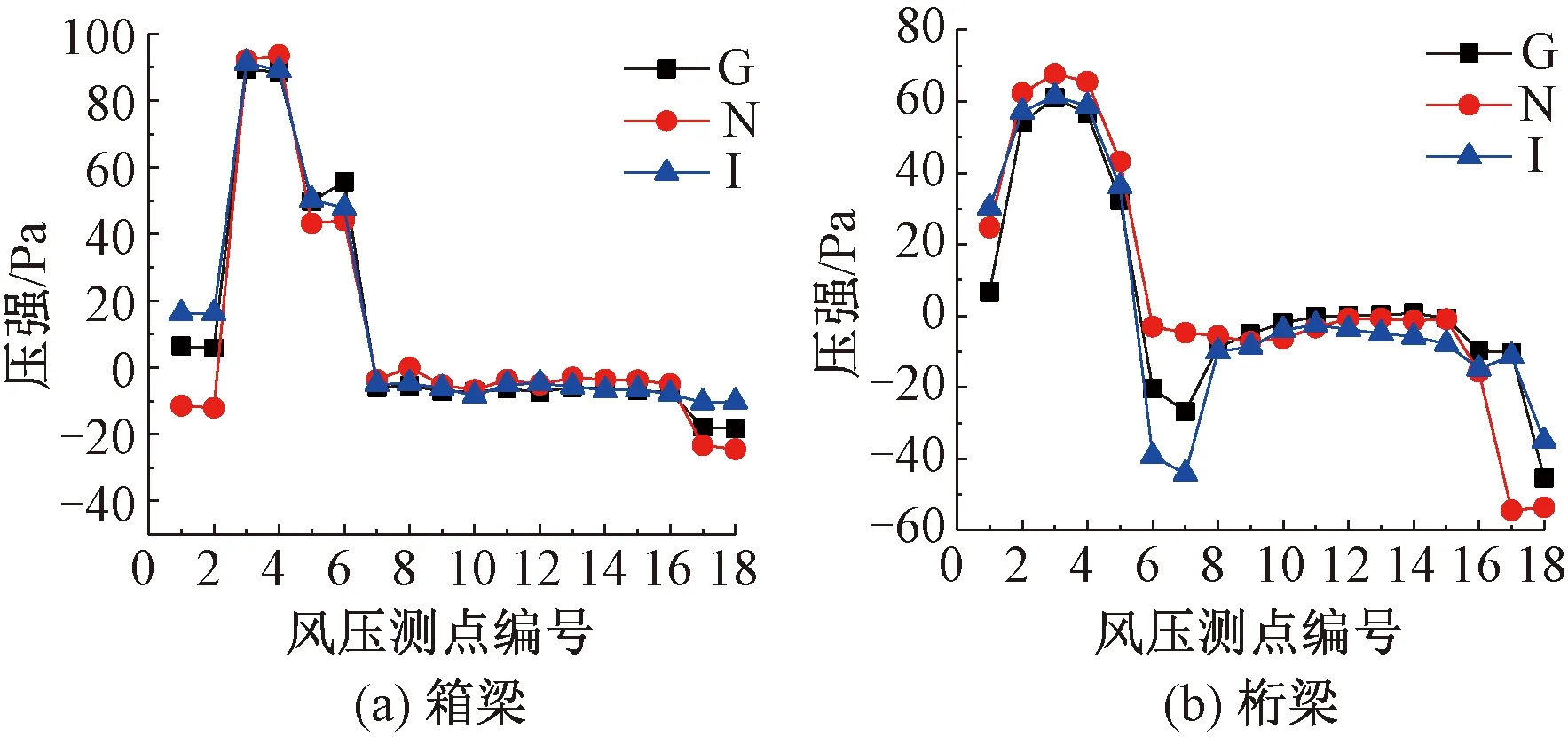
图5 列车的表面风压对比

当来流风速为9 m/s，风攻角为零时，列车在两种梁上的三分力系数见表1。由表1可知，列车在桁梁上的三分力系数显著低于其在箱梁上的结果。其中，力矩系数由于方向相反差异最大，约为150%；阻力和升力系数也分别相差34%和83%。

表1 列车的三分力系数对比

箱梁和桁梁上车辆的三分力系数随风攻角的变化曲线见图6。由图6可以知，当风攻角在-6°～6°范围内变化时，车辆在桁梁上的升力系数均低于其在箱梁上的结果。正攻角时车辆在桁梁上的力矩系数也低于其在箱梁上的结果，但负攻角时前者高于后者。当风攻角在-6°～4°范围内变化时，车辆在桁梁上的阻力系数低于其在箱梁上的结果，但当风攻角增至6°时，前者略高于后者。

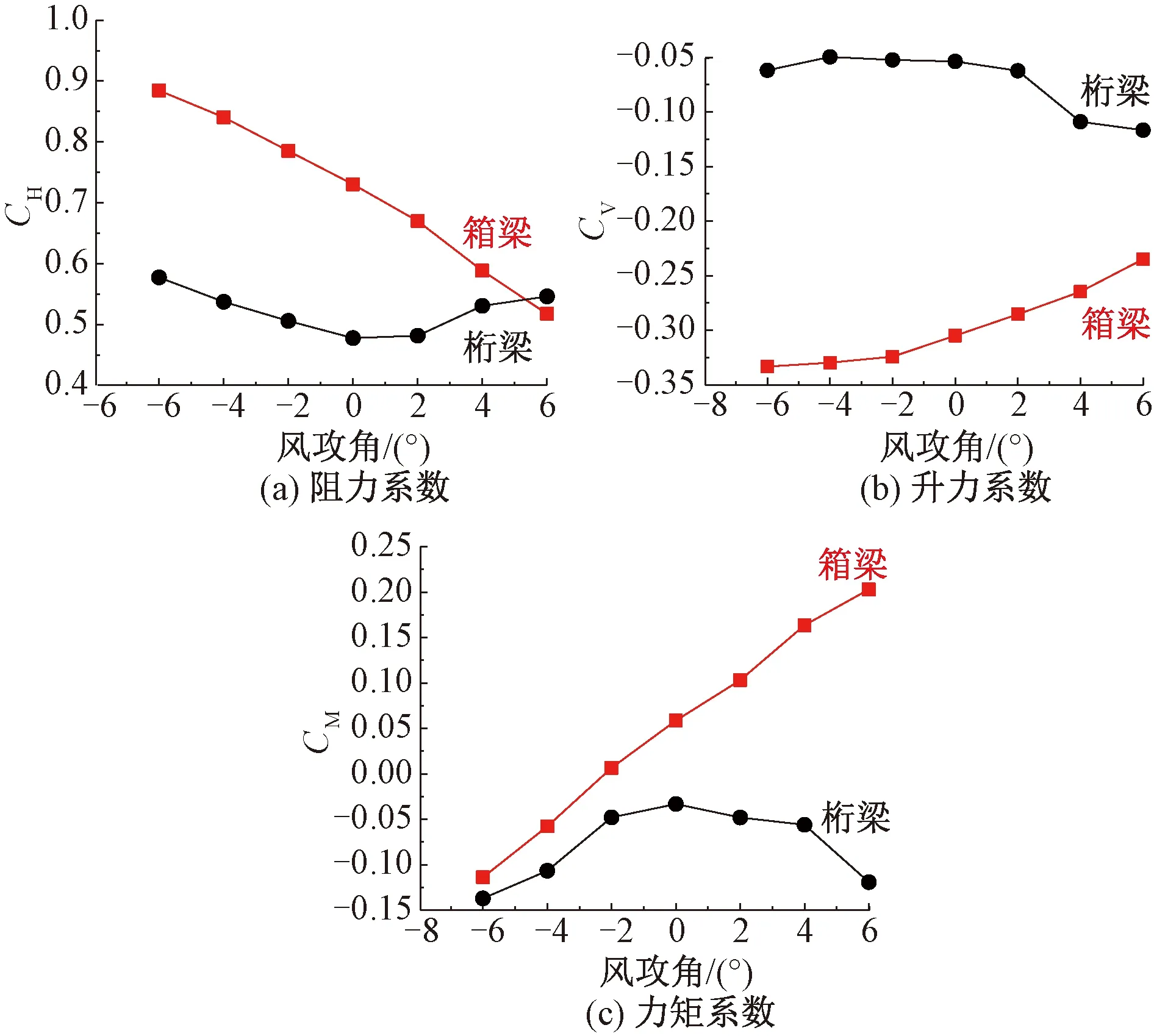
图6 列车的三分力系数对比

2.4 列车头车及中间车的三分力系数对比

当列车位于桁梁上，头车和中间车(车厢1)各测压面的风压分布见图7。由图7可知，由于气流绕流效应，头车较中间车的迎风侧表面风压略高。头车和中间车的最大风压值分别为67.31、65.47 Pa。

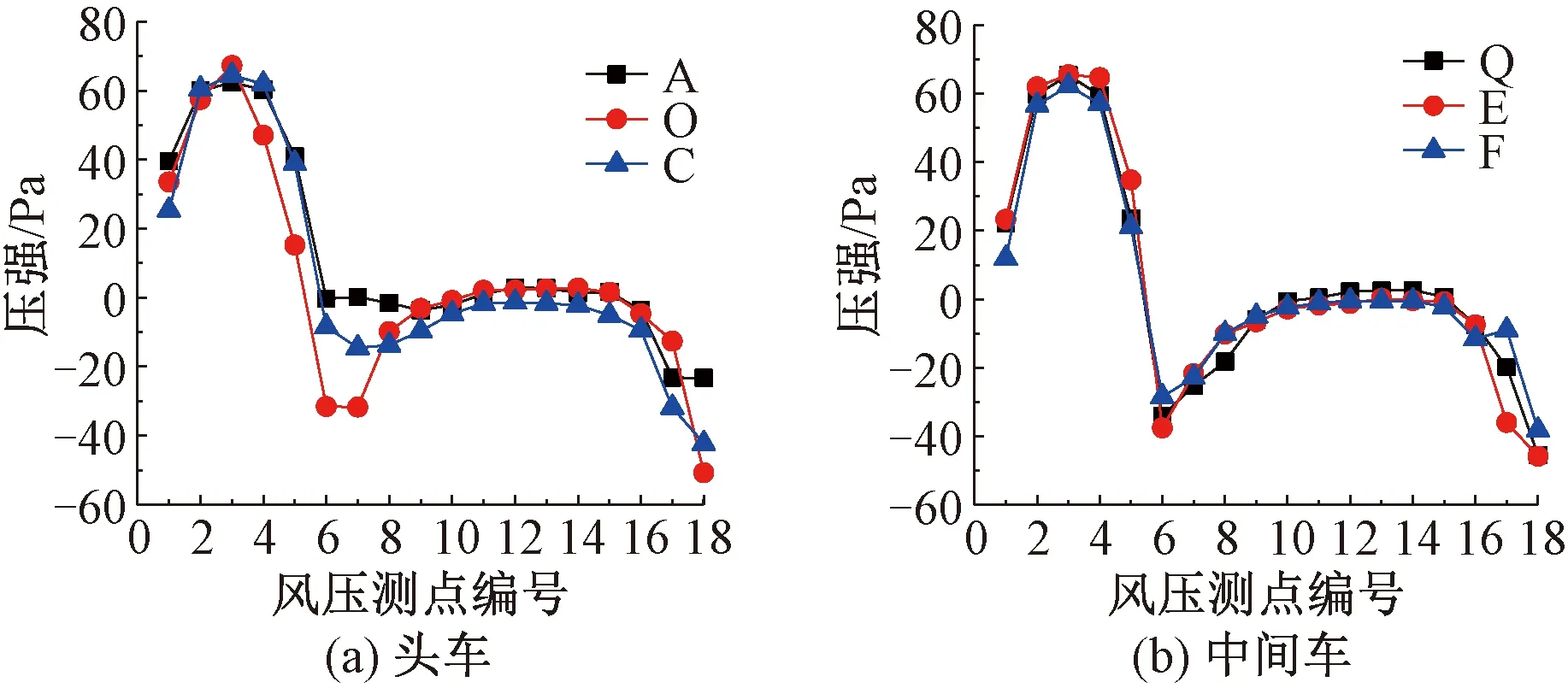
图7 头车和中间车的表面风压

零攻角时头车和中间车的三分力系数见表2。由表2可知，头车的结果较大，阻力、升力和力矩系数分别比中间车高4%、300%和33%。这一结论与文献[15]的结论相似。

表2 头车和中间车的三分力系数

头车和中间车的三分力系数随风攻角的变化曲线见图8。由图8可知，当风攻角在-6°～6°范围内变化时，头车的阻力系数和力矩系数均高于中间车；当风攻角在-6°～4°范围内，头车的升力系数也高于中间车，但当风攻角增至6°时，中间车的升力系数略高于头车。

图8 头车和中间车三分力系数

3 桁架结构内部风环境数值分析

3.1 数值模型的建立

为了研究桁架内部风场，采用大型流体仿真软件Fluent分别建立了直达25 T列车-桁梁系统模型和单独桁梁模型。模型比例与风洞试验保持一致，几何模型缩尺比均采用1∶80。综合考虑计算精度和效率，选取计算域长度为10 000 mm，高度为5 000 mm，宽度为1 260 mm，如图9所示。设定来流面入口为速度入口，试验来流为9 m/s的均匀流；出口面为压力出口；流体域上、下及两侧面设置为对称边界，桁梁表面设置为无滑移壁面边界。

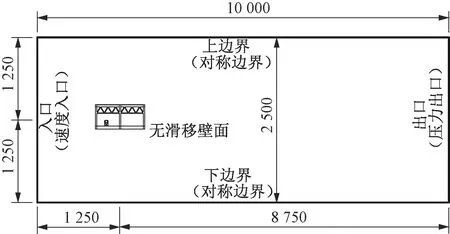
图9 计算域及边界条件(单位：mm)

如图10所示，对流体域采用混合网格划分，其中桁梁附近区域采用非结构化网格，最小网格尺寸为3 mm；远离桁梁的区域由于流体受到的湍流扰动相对较小，采用结构化网格划分，网格尺寸相对较大。列车-桁梁模型和单独桁梁模型的网格数量分别为434万和398万，两种模型的网格歪斜角均小于0.95，网格最大纵横比均小于5∶1，计算时采用RNGk-ε湍流模型，使用SIMPLE算法，压强采用标准空间离散，力矩、湍流强度及湍流耗散率采用二阶迎风差分模式离散。

图10 模型网格划分

3.2 与风洞试验结果的比较

为验证所建立的数值模型的精度，选取零攻角时桁梁和车厢2的三分力系数与风洞试验结果进行对比，见表3。由表3可知，数值模拟与风洞实验得到的阻力系数十分接近，列车和桥梁的阻力系数误差仅为7%和6%。但升力系数和力矩系数由于桁架内部风场十分复杂且本身较小，差别较大。

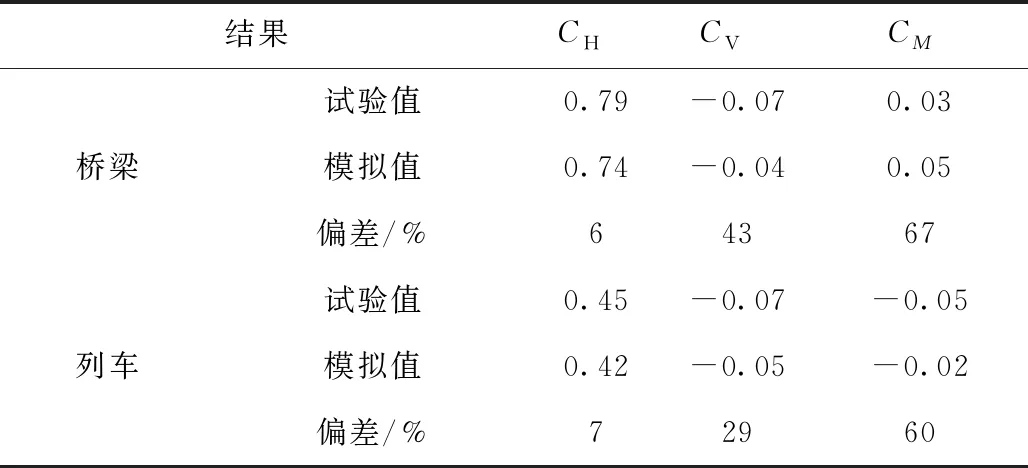
表3 风洞试验和数值模拟结果对比

3.3 等效风速及侧风折算系数

为了衡量桥面侧向风速的大小，基于总风压相等的原则，庞佳斌等[16]、夏锦林等[17]提出了二维等效风速的计算公式为

(3)

式中：Ueff为等效风速；Heq为等效风速计算高度；z为距桥面的高度；U(z)为高度z处的侧风风速。

由于桁架结构杆件多，空间布置复杂，无法以某个截面的气动特性来代替桁梁整体的气动特性，在引入等效风速时，需对式(3)进行修正。修正后桁梁断面的等效风速Ueff计算公式为

(4)

式中：Seq为等效风速所需积分的面积；U(s)为积分面积上的风速；n为积分面的个数。

为研究桁架结构的遮风效应，引入另一个无量纲参数——侧风折算系数η，它可表示为等效风速Ueff与来流风速U的比值，即

(5)

3.4 等效风速计算点布置方案

当来流风速为9 m/s时沿桥梁长度方向的风速分布图见图11。由图11可知，桁架内部风场由于杆件的规则布置而具有周期性的分布，这与文献[4]得到的结论相似。

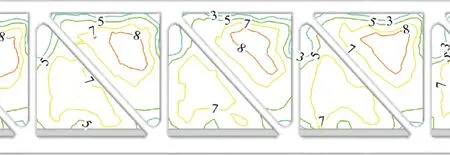
图11 风速等值线图(单位：m/s)

根据桁架内部风场的周期性分布特性，选取一个桁架节间对其进行细化分析。如图12所示，节间长为190 mm，宽为438 mm，高为223 mm。由于在不同位置处来流风所受到的结构遮挡不同，即使是均匀流经过桁架，风速分布也会有较大差异。为了更好地研究结构风场效应，将该节间沿长度方向等间距划分了7个横断面，间距为30 mm，见图12(a)。每个横断面在两个挡砟墙范围之内共布置了540个等效风速计算点，相邻计算点沿桥梁宽度方向相距10 mm，高度方向相距12.5 mm，见图12(b)。总计在该节间内部布置了3 780个等效风速计算点，通过分块积分来获得节间内部的等效风速。

图12 等效风速计算点布置图(单位：mm)

3.5 各车道的等效风速分布

桁架下层桥面车道1～车道4的等效风速随高度的变化曲线见图13，为了表示方便，竖坐标轴采用距桥面的相对高度z/h，h为桁梁的高度。由图13可知，迎风侧两个车道(车道1、2)上方的等效风速较大；在各车道上方0.15h～0.45h高度处的等效风速较大，在6.31 m/s以上；最大等效风速发生车道1上方0.25h附近，约为7.11 m/s。这一高度与车体形心高度较为吻合，值得引起注意。

图13 各车道的等效风速

为进一步分析横风流经桁架结构后的三维分布情况，将等效风速沿桥梁横向y、竖向z、纵向x三个坐标轴方向进行分解，可分别得到横桥向(ueff)、竖向(weff)和顺桥向(veff)三个等效风速分量，见图14。

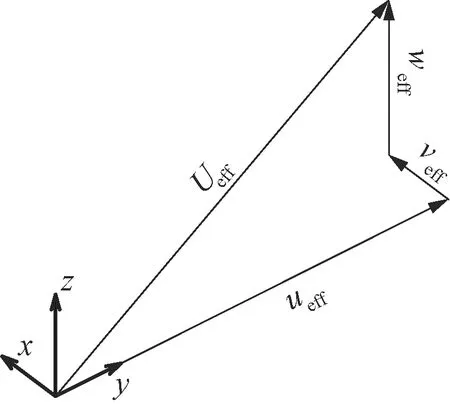
图14 等效风速分解示意

各车道分解后的等效风速分量随高度的变化曲线见图15。由图15可知，横桥向等效风速数值较大，而顺桥向等效风速和竖向等效风速的数值较小，三个方向风速分量占总风速的比重分别为98.7%、5.9%、14.8%。随着高度的增大，横桥向等效风速呈先增大后减小的趋势，而顺桥向和竖向等效风速的变化较为紊乱。

四条车道的侧风折算系数的最大值、均值和方差见表4。由表4可知，从车道1～车道3，最大侧风折算系数逐渐递减，但到车道4略有反弹。车道2的侧风折算系数方差最小，说明此处等效风速波动最小。

3.6 桁架横断面等效风速分布

当来流风速为9 m/s时，桁梁某一横断面的等效风速等值线图见图16。该断面左半部为迎风侧，右半部为背风侧。由图16可知，断面上的等效风速明显低于来流风速，迎风侧和背风侧的平均风速分别为5.49、5.34 m/s，约为来流的61%和59%。图16中Ⅰ和Ⅱ分别为迎风侧和背风侧等效风速较高的两个区域，最大风速分别为7.22、6.95 m/s。

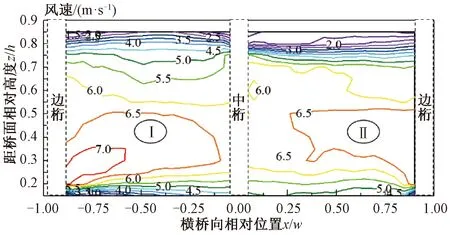
图16 横断面等效风速等值线图

该横断面受桁架杆件的遮挡效应可用侧风折算系数来衡量。侧风折算系数随高度、桥宽分布的曲线见图17，w为桁梁宽度。由图17可知，最大侧风折算系数发生在迎风侧坐标(-0.63w，0.25h)处，最大侧风折算系数达到0.80，也即此时结构对来流风的遮挡在20%以上。

图17 横桥向侧风折算系数

3.7 桁架纵断面等效风速分布

当来流风速为9 m/s时，一个桁架节间的等效风速等值线图见图18。由图18可知，在桁架的上、下弦杆及竖杆附近区域，迎风面的等效风速高于背风面；但在靠近斜杆附近区域，背风面的等效风速高于迎风面。迎风面和背风面的平均风速分别为5.52、5.43 m/s，约为来流的61%和60%。在被斜腹杆分成的两个直角三角形区域的形心附近(Ⅲ、Ⅳ、Ⅴ和Ⅵ)等效风速较高，各区域的最大风速分别为7.77、7.76、7.67、8.29 m/s。

图18 桁架节间等效风速等值线图

迎风面和背风面不同高度处的侧风折算系数的最大值、均值和方差见表5。由表5可知，迎风面和背风面最大侧风折算系数分别为0.86和0.92；距桁架下层桥面越高，方差越大，表明风速波动越剧烈；相同高度处背风面比迎风面的风速波动大，这可能是由于受到了中桁的阻碍和挤压所形成。

表5 桁架节间侧风折算系数统计值

4 结论

通过风洞试验和数值模拟，研究了列车-桁梁、列车-箱梁系统的气动特性以及桁架结构内部风速场的空间分布特征，得到如下结论：

(1)在小攻角下，桁梁的阻力、升力及力矩系数明显低于箱梁。零攻角时，桁梁的阻力、升力及力矩系数分别较箱梁减小了58%、89%、85%。

(2)列车在桁梁上的表面风压最大值较其在箱梁上低30%，但由于车厢顶部受到桁架的遮挡，出现了一个波动较大的负压。零攻角时，列车在桁梁上的阻力、升力、力矩系数约为其在箱梁上的66%、17%、50%。

(3)由于气流绕流效应，头车较中间车的迎风侧表面风压略高。零攻角下，头车的阻力、升力和力矩系数分别比中间车高4%、300%和33%。

(4)车道上的等效风速分布规律：横风流经桁架结构出现了三维分布，其中横向风速分量ueff所占比重最大，约为总风速的98%以上；迎风侧两个车道(车道1、2)上方的等效风速较大；车道1～车道3的风速呈递减趋势，但到车道4略有反弹；车道2的风速波动最小；在各车道上方0.15～0.45倍梁高处的风速较大，最大风速发生在车道1上方0.25倍梁高附近，该高度接近车体形心高度，值得引起注意。

(5)从桁架横、纵断面的等效风速分布可以看出，桁架结构内部的平均风速显著低于来流风速，平均侧风折算系数不超过0.61，表明桁架结构对来流风的遮挡平均在40%左右。但在被斜腹杆分割而成的两个直角三角形区域的形心附近出现了高风速，最大侧风折算系数达到了0.92。

(6)数值结果表明，对桁架结构内部风速场及车桥系统风荷载进行计算模拟时，不能简单采用不变的平均风理论，而需综合考虑桁架的遮风效应、构件对气流的阻碍、挤压效应以及横风通过桁架的空间分布规律等合理确定。