真双极柔性直流系统单极接地故障熄弧时刻识别策略

2022-07-12宁家兴和敬涵梁晨光罗易萍陈可傲

电力系统自动化 2022年13期

宁家兴，和敬涵，李猛，梁晨光，罗易萍，陈可傲

（北京交通大学电气工程学院，北京市 100044）

0 引言

柔性直流输电作为新一代直流输电技术，潮流控制灵活，不易发生换相失败，在世界范围内被广泛关注［1］。柔性直流输电网一般采用架空线路进行功率传输，而架空线路易受到环境因素影响发生故障，且多为瞬时性故障［2-4］。自动重合闸可在瞬时性故障后快速恢复潮流［5-6］，提升柔性直流输电的可靠性。然而，自动重合闸缺乏故障状态判别环节，当重合于永久性故障时，会对整个系统造成不必要的二次冲击，尤其是柔性直流系统阻尼低、故障电流上升速度快以及电力电子器件过流能力弱，对二次冲击的承受能力更差［7-9］。因此，在断路器重合前对故障性质进行判别，实现自适应重合闸就显得尤为重要。

根据是否需要依赖外界注入信号，可以将现有直流自适应重合闸的研究分为主动注入式和被动识别式两大类［10-14］。文献［10］通过向故障极线路注入电压信号，利用行波折反射和低压判据区分故障类型；文献［11］通过向系统注入特定频率的交流信号，提取线路上电气量响应作为故障特征量来实现永久性故障判别；文献［12］利用两极线路间的耦合特性，通过向健全极线路注入特征信号，检测故障极是否存在耦合信号来辨别故障状态。上述主动注入式方法需要考虑注入的信号是否会影响系统的正常运行，且只适用于特定的拓扑结构，需要改变换流器原有的控制，实现起来有一定难度。对于被动识别式方法，文献［13］分析了故障消失后的故障极残压特性，通过对阈值进行整定来识别故障性质，但该方法缺乏对故障消失前残压特性的分析，故障消失前的残压可能会影响判据的可靠性；文献［14］通过检测正负极电压之差是否为零来识别永久性故障，但该方法仅适用于双极短路故障。

上述方法普遍只注重于故障性质判别，而忽视了对瞬时性故障熄弧时刻的进一步识别，采用固定的重合闸时间。若瞬时性故障熄弧时间较慢，可能会由于没有充分地去游离，导致断路器合闸失败，降低系统可靠性［15］；而对于熄弧较快的瞬时性故障，固定的合闸延时会导致系统不必要的非全极运行，不利于快速恢复供电。因此，重合闸的自适应不仅应体现故障性质自适应，还应包含合闸时间自适应。要实现合闸时间的自适应，就需要对瞬时性故障熄弧时刻进行识别。文献［16］针对双极短路故障提出一种基于线路残压主频率的熄弧时刻识别策略，但该策略需在频域中实现，计算复杂度高，且无法应用于发生概率较高的单极接地故障。文献［17］提出利用熄弧前后过渡电阻差异识别电弧性故障并确认熄弧时刻，但该方法只针对交流系统，应用于直流系统的有效性还有待进一步验证。相比于交流系统，直流系统中断路器重合于故障未熄弧状态对系统造成的危害更大［18］。因此，亟须对直流系统瞬时性故障熄弧时刻识别方法展开深入研究。

本文以真双极柔性直流输电系统为研究对象，利用PSCAD/EMTDC 仿真软件搭建一、二次电弧动态模型，实现故障电弧熄弧过程的模拟。通过对瞬时性故障熄弧前、后故障极端电压暂态、稳态特性进行理论分析，揭示故障极端电压在熄弧前后特征差异的机理。进一步，利用积分比算法提取该差异，提出了一种适用于真双极柔性直流系统发生单极接地瞬时性故障时的熄弧时刻识别策略。

1 故障电气量特性分析

1.1 故障阶段划分

借鉴交流系统经验，直流系统发生单极接地瞬时性故障后故障极端电压可以根据不同时间节点划分为几个阶段，如图1 所示。

图1 故障阶段划分Fig.1 Fault stage division

图1 中，t0至t3时刻分别表示故障发生、断路器断开、电弧熄灭、断路器合闸。故障发生前，D0为系统正常运行阶段；在故障发生到断路器断开之间，维持电弧燃烧的能量主要由电源侧供给，称D1为一次电弧阶段；在断路器断开后到电弧熄灭前，电源能量被切除，维持电弧燃烧的能量主要由健全极的耦合作用来提供，称D2为二次电弧阶段；当电弧熄灭、接地点消失之后，在健全极的耦合作用下，故障极端电压开始出现恢复，称D3为恢复电压阶段；D4为断路器合闸后的正常运行阶段。

1.2 故障电弧特性

要实现熄弧时刻的可靠识别，首先要对故障电弧的特性进行准确模拟，长间隙空气电弧模型（包括一次电弧模型和二次电弧模型）能够较为准确地模拟出故障电弧的非线性特性及自熄特性［19-20］，下面分别对一、二次电弧的动态特性进行分析，为后续建模仿真提供理论基础。

1.2.1 一次电弧动态特性

一次电弧阶段为故障发生到断路器断开之间的阶段，该阶段维持电弧燃烧的能量主要由电源侧供给，使得故障点流过较大的短路电流，一次电弧燃烧稳定，长度变化不大。一系列研究表明，一次电弧的动态特性可以大致由式（1）表示［19］：

式中：Rpri为一次电弧电阻；gp为一次电弧电导；Lp为一次电弧长度，Lp=400 cm；Ip为一次电弧的电流峰值，Ip=14 kA；比例系数α=2.85×10-5；ip为一次电弧电流；Vp为一次电弧单位长度稳态电弧电压梯度，通常电流在1.4～24 kA 范围内Vp=15 V/cm。

1.2.2 二次电弧动态特性

断路器断开后到电弧熄灭前为二次电弧阶段，二次电弧的动态特性远比一次电弧复杂，由于电源侧能量已经随着断路器断开而切除，依靠健全极耦合产生的电弧电流比一次电弧电流要小很多。且在二次电弧期间，电弧长度有明显的拉长。二次电弧动态特性可由式（2）模拟［20］。

式中：Rsec为二次电弧电阻；gs为二次电弧电导；is为二次电弧电流绝对值；Is为二次电弧的电流峰值，Is=35 A；比例系数β=2.57×10-3；tr为二次电弧持续时间；Ls为二次电弧长度，低风速（0～1 m/s）环境下可通过式（3）求得。

式中：L0为二次电弧初始长度，即一次电弧长度。

与一次电弧不同，二次电弧会经历“燃烧—熄灭—重燃—熄灭”的复杂反复过程，直到电弧电流为0 且二次电弧的实际电压幅值始终小于重燃电压，二次电弧才彻底熄灭，重燃电压Vr的经验公式为：

式中：Te为电弧出现到电弧熄弧间的时间（包括电弧临时熄灭与永久熄灭）；h（tr-Te）为延迟单元阶跃函数，其作用是用来控制重燃电压计算生效的时段。仿真时Te和tr-Te的计算利用PSCAD/EMTDC 环境中的Fortran 语言编写自定义脚本实现。

由于一、二次电弧存在的时间段不同，因此在建模时需要控制一次电弧电阻和二次电弧电阻的输出时段，最终输出的电弧电阻可通过下式表示：

式中：Rarcall为最终输出的电弧电阻；Rext为熄弧电阻，可取足够大的阻值1050Ω 来模拟电弧支路消失（开路）；t0为故障发生时刻；t1为断路器断开时刻；txj为第j次二次电弧熄灭时刻；tyj为第j次二次电弧重燃时刻，j=1，2，3，…。

1.3 故障极端电压特性

通过对二次电弧阶段（熄弧前）和恢复电压阶段（熄弧后）的电气量特性差异进行分析可知，故障极端电压在故障熄弧前后存在明显差异且方便获取，故本文选取故障极端电压作为特征电气量。

1.3.1 熄弧前故障极端电压

真双极柔性直流输电线路发生单极接地故障，故障极端电压由测量端至故障点间的电压降和故障点电压组成。断路器断开后，测量端至故障点的电压降其实就是健全极负荷电流通过极间互感在故障极上产生的电磁耦合电压［21］。而对于直流输电线路来说，极间互感作用十分微弱，电磁耦合电压可以忽略不计［13］。因此，故障极端电压主要由故障点电压组成，故障点电压可通过故障支路阻抗乘上流过故障支路的电流求得。由于断路器已经断开，流过故障支路的电流主要由健全极通过极间电容和极对地电容所产生的静电耦合作用提供。与交流输电线路不同的是，直流输电线路极-极和极-地间存在离子流，离子流从物理意义上可以用电导表示［13，22］，因此还应考虑极间电导和极对地电导。故障熄弧前，故障点通过电弧电阻以及过渡电阻接地，故障极端电压等效电路如图2 所示。其中，Cm、C0分别为极间耦合电容和极对地耦合电容，gm、g0分别为极间电导和极对地电导，Rarc为电弧电阻，Rtrst为过渡电阻，um为极间耦合电压，u0为故障极端电压，u1、u2分别为正负极等值电压源。根据基尔霍夫电流、电压定律可得：

图2 故障熄弧前故障极端电压等效电路Fig.2 Equivalent circuit of fault pole voltage before fault arc extinction

式中：Usp为二次电弧阶段初始时刻故障极端电压；τs为二次电弧阶段时间常数。

由式（7）可以看出，二次电弧阶段故障极端电压主要由健全极电压u1所产生的零状态响应分量和二次电弧阶段初始时刻故障极端电压Usp所产生的零输入响应分量组成。其中零状态响应分量可进一步整理为：

式中：uzss为二次电弧阶段故障极端电压零状态响应分量。

以某直流电网工程参数为参考，由于健全极电压u1的数量级为105V，gm的数量级通常小于10-7Ω，Rarc和Rtrst的数量级小于102Ω，因此uzss系数项的数量级通常小于100V，而零输入响应分量系数项的数量级通常为104～105V。因此，零状态响应分量可以忽略不计，二次电弧阶段故障极端电压的变化趋势主要取决于零输入响应，可以认为故障极端电压暂态值近似为：

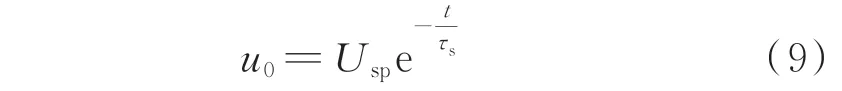
从式（9）可以看出u0的变化趋势为指数衰减，因此熄弧前故障极端电压整体呈现一种指数衰减的趋势。而稳态时，Cm、C0等于0，即τs=0，可推导出故障极端电压的稳态值U0s为：

从式（10）可见，故障极端电压稳态值最终稳定在一个接近于0 的较小值。因此，从上述分析可知，二次电弧阶段故障极端电压逐渐衰减并趋近于0。

1.3.2 熄弧后故障极端电压

故障熄弧后输电线路静电耦合和离子流作用仍然存在，故障支路消失，故障极端电压进入恢复电压阶段。图3 为熄弧后故障极端电压等效电路。

图3 故障熄弧后故障极端电压等效电路Fig.3 Equivalent circuit of fault pole voltage after fault arc extinction

与故障熄弧前的推导过程类似，根据基尔霍夫电流、电压定律可得：

进一步求解得到故障熄弧后故障极端电压为：

式中：Urp为恢复电压阶段初始时刻故障极端电压，可认为Urp=U0s；τr为恢复电压阶段时间常数。

同样地，由式（12）可以看出，恢复电压阶段故障极端电压也是由零状态响应分量和零输入响应分量组成。其中，零状态响应分量可进一步整理为：

式中：uzsr为二次电弧阶段故障极端电压零状态响应分量。

由于g0＞gm，并且数量级上通常是gm的1～102倍［23］，因此uzsr系数项数量级通常为103～105V，而式（12）中Urp=U0s，其数值是一个接近于0 的较小值，因此，零输入响应分量可以忽略不计。恢复电压阶段故障极端电压的变化趋势主要取决于零状态响应，可以认为故障极端电压暂态值近似为：

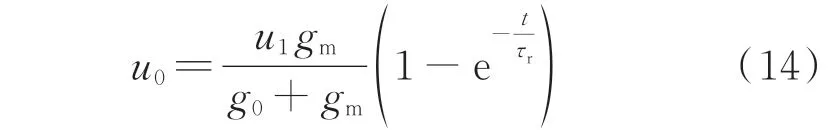
从式（14）可以看出u0的变化趋势为对数上升，因此熄弧后故障极端电压整体呈现一种对数上升的趋势。稳态时，τr=0，可得故障极端电压稳态值为：

由式（15）可知，故障极端电压稳态值最终稳定在数量级为103～105V 的值，并且由于g0＞gm，因此，必定满足U0r＜u1/2。因此，从上述分析可知，恢复电压阶段故障极端电压逐渐上升并稳定在U0r。

2 真双极柔性直流系统熄弧时刻识别策略

由前文分析可知，二次电弧阶段由于故障支路还未消失，故障极端电压逐渐衰减趋近于0。而恢复电压阶段故障支路消失，由于健全极对故障极的耦合作用，使得故障极端电压出现恢复并趋于一个稳定值。基于此，本文提出一种积分比算法，通过获取每相邻两个时间窗信号积分的比值，来提取故障极端电压熄弧前后的差异。

2.1 积分比算法

由于实际输电线路为分布参数，因此断路器断开后故障极端电压不会只呈现理论分析的指数衰减，还会含有振荡分量，使得熄弧前故障极端电压呈现振荡衰减的趋势，为避免振荡对积分比算法识别结果产生影响，选取故障极端电压绝对值信号作为积分比对象。积分比过程如图4 所示。

图4 积分比过程示意图Fig.4 Schematic diagram of integral ratio process

图4 中：TS为移动步长，i为移动次数（i=0，1，2，…），TW为时间窗长，A0和B0分别表示初次检测到的相邻时间窗积分值，K0为初次检测时的积分比，Ai和Bi分别表示移动i次时检测到的相邻时间窗积分值，Ki为移动i次时的积分比。在t1时刻断路器断开后等待2TW时长，tstart时刻开始检测，依次对每2 个相邻时间窗内故障极端电压的绝对值信号uamp进行积分得到Ai和Bi，进一步求得每相邻2 个时间窗积分的比值为：

式中：ti=t1+2TW+iTS。

2.2 熄弧时刻识别流程

熄弧时刻识别流程如附录A 图A1 所示，具体识别方案如下：

1）当发生单极接地故障时，故障极断路器断开后，提取故障极端电压信号u0；

2）计算故障极端电压绝对值信号uamp=|u0|，依次求得uamp在每相邻2 个时间窗内的积分值Ai和Bi；

3）依次求得每相邻2 个时间窗的积分比Ki；

4）为保证检测结果的可靠性，设定阈值Kset，当Ki≥Kset时，说明故障已熄弧，但为避免偶然性，规定若检测到Ki≥Kset在连续Tc时间内恒成立才判断故障已熄弧，假设判断故障已熄弧时刻为tend，则检测到熄弧时刻（首次超过阈值的时刻）tarc=tend-Tc。

2.3 阈值整定原则

1）阈值Kset

检测方案中阈值Kset的设置原则如图5 所示。

图5 阈值整定示意图Fig.5 Schematic diagram of threshold setting

图5中，t2为故障实际熄弧时刻，tarc为积分比K=1的时刻。由1.3 节理论分析可知，故障熄弧前故障极端电压呈现指数衰减趋势，而熄弧后故障极端电压呈现对数上升趋势。因此，从开始检测到故障熄弧时间段（tstart≤t≤t2）内的积分比必定始终满足K＜1，而故障熄弧又经过2 个时间窗之后时间段（t≥t2+2TW）内的积分比必定始终满足K＞1，并且必定存在某时刻tarc∈（t2，t2+2TW），使得积分比K=1。因此，实际熄弧时刻所对应的积分比必定满足K＜1，即当K=1 时故障必定已熄弧，且K=1 时刻与实际熄弧时刻的时间差满足小于2TW。即若将阈值设置为1，能够将熄弧时刻检测误差控制在2 个时间窗之内。这样，在保证了检测可靠性的同时，检测精度也能得到保证。因此，设置阈值Kset=1。

2）循环判断时间Tc

Tc的设置首先需要保证不超过绝缘恢复时间，即首先应满足Tc＜100 ms。另外，考虑到熄弧后故障极端电压上升趋势逐渐变缓，因此图5 中t2+2TW时刻之后的时间里积分比都会小于t2+2TW时的积分比，故在t2＜t＜t2+2TW时间段内积分比结果的可利用度最高，因此设定循环判断时间Tc=2TW。

3）时间窗TW

对图5 分析可知，K=1 的时刻与实际熄弧时刻相差的时间范围为（0，2TW），并且还要考虑循环判断时间2TW和绝缘恢复时间。因此，时间窗TW的选取应满足：

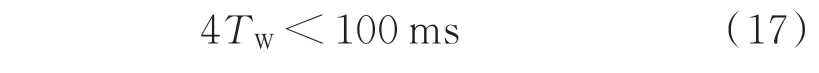
综合考虑，本文设定时间窗TW=20 ms。

4）移动步长TS

本策略中选取TS=250 μs，即每隔250 μs计算1个积分比值，算法采样频率为4 kHz，根据文献［24］可知，张北柔性直流工程保护的采样频率是10 kHz，本文算法对采样频率要求不高，能够满足实际工程需求。

2.4 与重合闸的时间配合

所提熄弧时刻识别策略在故障跳闸后即开始检测，经过40 ms（积分比的2 个相邻时间窗）获得第1 个积分比值。当检测到故障熄弧后，并不能立刻发出合闸指令，因为弧道的绝缘恢复需要一定的时间。对于500 kV 电网，绝缘恢复时间可取100 ms，而这100 ms 中还有40 ms 的循环判断时间［15］。因此，在经过循环判断确定出电弧熄灭后只需再经过60 ms 即可对重合闸发出指令，进行合闸操作。

2.5 成效对比分析

为突出熄弧时刻识别策略对优化重合闸时间的意义，将结合本文所提策略的自适应熄弧时刻重合闸与未结合本文所提策略的自动重合闸进行对比。图6 为不同重合闸策略对比图。

图6 不同重合闸策略对比Fig.6 Comparison of different reclosing strategies

对于常规自动重合闸，在断路器断开后，需要等待300 ms 固定去游离时间才能合闸［9］。而能够自适应熄弧时刻的重合闸，可在断路器断开后实时检测故障是否熄弧，在判断出故障熄弧后，只需再等待60 ms 绝缘恢复完成即可进行合闸操作。相比于常规自动重合闸，结合本文所提熄弧时刻识别算法的重合闸能够在一定程度上优化合闸时间，这对于故障后供电的快速恢复具有重要意义，能够提高柔性直流系统供电的可靠性和经济性。

3 影响因素分析

3.1 燃弧时间

由于实际故障电弧燃烧时间长短不一，而本文所提策略是在断路器断开后经过2 个时间窗开始检测的，因此可能出现检测开始前故障已熄弧的情况，有必要分析燃弧时间长短对所提熄弧时刻识别策略的影响。分析结果如附录A 图A2 所示，K0表示初次检测时的积分比，Km和Kn分别表示时间窗移动m、n次时的积分比。

3.2 过渡电阻

过渡电阻主要影响二次电弧阶段（熄弧前）故障极端电压的特性，由式（7）和式（10）容易看出，过渡电阻越大，时间常数越大，二次电弧阶段故障极端电压衰减越慢，且故障极端电压稳态值越大。过渡电阻影响的是熄弧前故障极端电压衰减的快慢及故障稳态时故障极端电压值的大小，而本文所提积分比判据是基于故障极端电压绝对值信号前后相邻2 个时间窗内积分值大小的比值，判据对于信号的衰减速率及幅值大小具有一定的耐受能力。并且高阻故障下，熄弧前故障极端电压的衰减越平坦，熄弧时刻检测的灵敏度会变高，从而使得熄弧时刻检测误差变小。因此，本文所提策略具备较强的过渡电阻耐受能力。

3.3 故障位置

故障位置仅影响由互感产生的电磁耦合量。对于直流系统而言，极间互感产生的电磁耦合影响较小［13］，因此，故障极端电压与故障位置关系不大，本文所提策略基本不受故障位置的影响。

3.4 噪声

实际工程中，信号在传输过程中会受到噪声干扰。噪声主要体现的是高频特性，而本策略所提积分比算法中的积分能够消除高频信号的影响，在有无噪声干扰的情况下积分值变化不大，因此积分比结果也基本不会变化太大，本文所提策略对噪声具有较好的耐受能力。

3.5 通信误差

通信误差主要影响的是基于双端量的判据，而本文所提策略只需提取单端量信息（故障极单端电压）即可，无需双端量信息的传输。因此，所提策略不会受到通信误差的影响。

3.6 电弧非线性和随机性

电弧在燃烧的过程中存在非线性和随机性，而本文积分比判据是基于熄弧前后故障极端电压先衰减后上升的趋势来实现的，电弧的非线性和随机性并不会改变故障极端电压的整体变化趋势，并且积分比算法的积分环节对信号的非线性和随机性具有一定的耐受能力，小的波动并不会影响最终的判断结果，因此电弧的非线性和随机性不会影响判据可靠性。

4 仿真验证

为验证所提真双极柔性直流系统熄弧时刻识别策略的有效性，利用PSCAD/EMTDC 软件搭建±500 kV 四端真双极柔性直流输电仿真系统，系统结构如附录B 图B1 所示。

4.1 参数设置

以架空线路1 为例，线路长度为200 km，线路模型选用依频模型，线路、杆塔结构、参数及系统主要设备参数参考张北柔性直流工程，分别见附录B 表B1、图B2、表B2。仿真时间设置如下：0 ms 发生故障，3 ms 保护发送跳闸信号，6 ms 断路器断开，实际的熄弧时刻由电弧模型进行模拟。

4.2 电弧模型

根据1.2 节的理论分析并结合文献［19-20］，在PSCAD/EMTDC 中搭建电弧仿真模型，其逻辑原理图如附录B 图B3 所示。逻辑原理图中的Te、tre采用Fortran 语言编写自定义脚本来实现，其他部分采用逻辑控制模块实现。

4.3 仿真结果分析

本文分别对真双极柔性直流输电线路不同故障位置经不同过渡电阻接地等故障情况进行大量仿真，以负极线路故障为例，选取其中2 种故障情景来进行分析，以验证所提熄弧时刻识别策略的有效性。

4.3.1 线路中点经100 Ω 过渡电阻接地

附录C 图C1 为真双极柔性直流输电线路中点经100 Ω 过渡电阻接地电弧特性的仿真结果。从图C1 可以看出，电弧电压呈现明显的“马鞍形”尖峰波特性，电弧电流呈现零休特性。故障电弧永久熄灭的条件为电弧电流为0 且电弧电压始终小于重燃电压。经过14 次临时熄弧后，在t=34.2 ms 后电弧电压便始终低于重燃电压且电弧电流也始终为0，满足永久熄弧条件，电弧永久熄灭，即电弧实际熄弧时刻为t=34.2 ms。本文所建电弧模型能够较好地反映故障电弧的非线性动态特性以及重燃特性，能够根据电弧电压、电流以及重燃电压自适应地模拟出电弧实际熄弧时刻，仿真结果与文献［19-20］中对电弧特性的描述一致，也验证了本文电弧模型的有效性。

附录C 图C2 为线路中点经100 Ω 过渡电阻接地时的熄弧时刻识别结果，从故障极端电压波形图可以看出，故障熄弧前（二次电弧阶段D2）故障极端电压呈现逐渐衰减的趋势并趋近于0，故障熄弧后（恢复电压阶段D3）由于正极线路的耦合，使得故障极端电压呈现恢复现象，再次验证了1.3 节理论分析的正确性。由于本文所提积分比算法利用每2 个相邻时间窗的积分进行计算，因此第1 个积分比值是在断路器断开后经过2 个时间窗（40 ms）时得到的。积分比首次超过阈值的时刻为t=56 ms，40 ms 后（t=96 ms）的积分比为1.435，积分比首次超过阈值后的连续40 ms 内始终大于阈值，可以确定故障已熄弧，并将t=56 ms 输出为检测熄弧时刻，而实际熄弧时刻为t=34.2 ms，误差仅为21.8 ms。

4.3.2 线路末端经300 Ω 过渡电阻接地

真双极柔性直流输电线路末端经300 Ω 过渡电阻接地电弧特性的仿真结果如附录C 图C3 所示。从图C3 同样可以看出，电弧电压与电弧电流能够较好地反映出故障电弧的非线性动态特性，最终在t=33.8 ms 时电弧永久熄灭，即实际熄弧时刻为t=33.8 ms。

附录C 图C4 为熄弧时刻识别结果，二次电弧阶段和恢复电压阶段（熄弧前后）故障极端电压的变化特性同样满足1.3 节理论分析，故障极端电压在t=33.8 ms 故障彻底熄弧后开始逐渐恢复，积分比首次超过阈值的时刻为t=62 ms，40 ms 后积分比为1.369，首次检测到超过阈值后的40 ms 内积分比始终大于阈值，因此，可以判断故障已熄弧，误差仅为28.2 ms。

4.4 普适性分析

为验证所提策略的普适性，分别对不同故障位置经不同过渡电阻接地下的仿真结果进行分析。仿真结果见附录C 表C1，其中Karc表示首次超过阈值时的积分比，Kend表示检测结束时的积分比。从表C1 可以看出，当线路发生瞬时性故障时，故障极端电压绝对值信号的积分比均满足首次超过阈值后连续40 ms 内Ki≥Kset，且结束检测时积分比值较大，不易造成误判。

4.5 噪声影响

实际柔性直流工程中的干扰信号主要包括电磁干扰和量测误差等，通常向采样数据中叠加高斯白噪声来模拟上述干扰的特征［25］。向故障极端电压中添加30 dB 白噪声［24-26］，以负极线路首端经100 Ω过渡电阻接地为例，验证噪声对所提策略的影响。附录C 图C5 和图C6 分别为电弧特性和熄弧时刻仿真结果。

从附录C 图C5 中可见，故障电弧实际熄弧时刻为t=38 ms。由图C6可知，检测到的熄弧时刻为t=70 ms，与实际熄弧时刻相比，误差为32 ms。为进一步确保所提策略的可靠性，后续将利用硬件在环试验来验证量测环节误差等因素对本文策略的影响。