采用改进积分反演法的四旋翼无人机容错控制

刘艳君 牛丽平

1(新乡学院计算机与信息工程学院 河南 新乡 453003) 2(河南师范大学计算机与信息工程学院 河南 新乡 453007)

Dynamic factor

0 引 言

由于四旋翼无人机(Four-rotor UAV)具有体积小、操控灵活和可悬停等优点，非常适用于复杂地形环境中的作业，已在军事侦察、农业监测、民用航拍及编队表演等领域发挥着越来越重要的作用[1-3]。四旋翼UAV主要依靠四个旋翼来提供动力，是一个多变量、欠驱动的旋翼式飞行系统[4]，对飞行控制系统的依赖性极高[5]。由于各旋翼执行器没有备份，当发生机械故障或者电气故障时，旋翼的执行器极易发生故障，此时需要飞行控制系统稳定跟踪指令信号，即实现UAV飞行容错控制[6-8]。

旋翼UAV的容错控制问题已经成为了学者们研究的热点。文献[9]针对四旋翼UAV的执行器故障问题，提出了一种鲁棒控制与故障估计器相结合的容错控制方法，实现了包容外部扰动和加性故障的UAV姿态跟踪。文献[10]针对四旋翼UAV的执行器故障问题，提出了一种基于STW的控制策略，并设计了高阶滑模观测器来估计故障程度，实现了包容执行器故障的稳定飞行。但是这类设计过程较为复杂，且需满足较为严格的假定条件。文献[11]针对UAV的执行器故障问题，提出了一种基于小波变换和等价空间的故障检测方法，将故障检测问题归结为小波基函数选取和等价空间向量的优化问题，以实现对执行器故障的检测与估计，并保持UAV稳定飞行。文献[12]针对三旋翼UAV建立了四元数倾转式动力学模型，设计了基于自适应观测器鲁棒容错控制器，实现了对发生故障时的无人机稳定控制。针对四旋翼UAV的执行器故障和干扰问题，本文在控制律设计中引入误差积分和动态因子，提出一种改进的积分反演容错控制方法，大幅提高了系统的动态性能和稳态性能。

1 四旋翼UAV建模及故障模型

1.1 四旋翼UAV动力学建模

四旋翼UAV有四个输入升力和六个运动方向的自由度，是多变量、欠驱动和强耦合的系统[13]。四旋翼UAV的结构示意图如图1所示。其中，旋翼1和旋翼3顺时针旋转，旋翼2和旋翼4逆时针旋转。

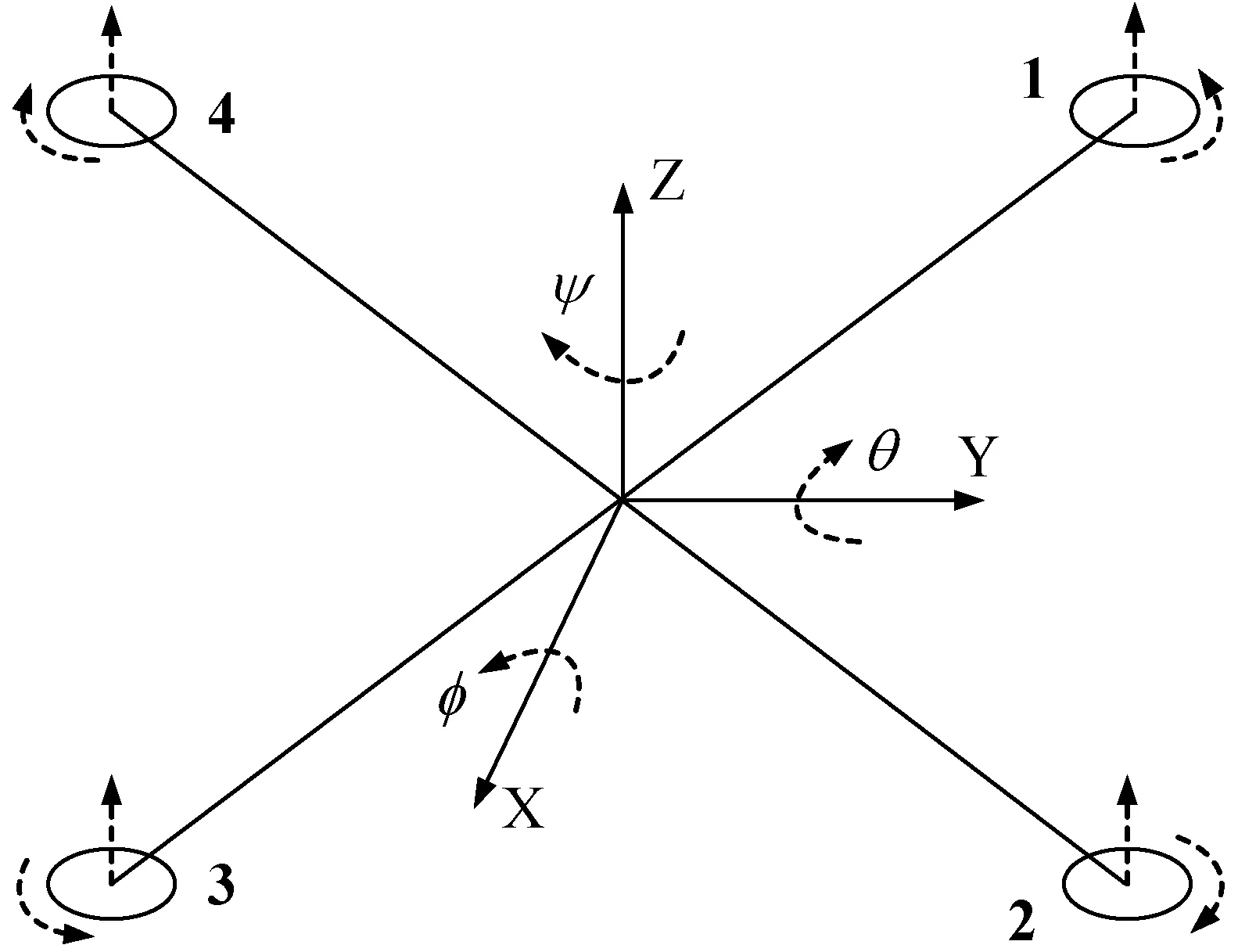
图1 四旋翼UAV结构

四旋翼UAV有三个机体轴，除可升降外，绕轴转动还可分别产生滚转、俯仰和偏航运动，四旋翼UAV模型[14]可以由以下方程描述：

(1)

(2)

(3)

(4)

式中：Ω1、Ω2、Ω3和Ω4分别为旋翼转速；KL和KN分别为升力系数和反扭矩系数；Jx、Jy和Jz分别为四旋翼UAV绕机体轴的转动惯量；Kx、Ky和Kz分别为机体轴方向的阻力系数；m和g分别为四旋翼UAV质量和重力加速度。

1.2 四旋翼UAV故障模型

四旋翼UAV是通过四个舵机带动四个旋翼转动来提供升力的，升力的大小与旋翼的转速相关。由于舵机长时间、高频率地转动，容易引起各部件的老化，会直接导致舵机执行器的效率下降，即发生失效故障。当UAV执行器发生失效故障时，舵机执行器不能带动旋翼按照需要的转速转动，这会严重影响整个UAV控制系统的稳定性和可靠性，威胁飞行安全。执行器失效故障主要表现为带动四个旋翼的转动效率下降，因此执行器失效故障可以描述为：

(5)

式中：F=diag(λ1,λ2,λ3,λ4)为执行器的失效故障系数矩阵，其中λ1,λ2,λ3,λ4∈(0,1]分别为四个舵机执行器的失效故障系数，用来反映舵机执行器带动旋翼转动的效率，λi=1(i=1,2,3,4)表示执行器未发生失效故障，λi∈(0,1)(i=1,2,3,4)表示执行器发生一定程度的失效故障。同时，考虑高度、滚转、俯仰和偏航四个回路的干扰项dh,dφ,dθ,dψ，则四旋翼UAV故障模型可描述为：

(6)

式(6)包含执行器失效故障及干扰项，本文针对此故障模型进行改进积分反演容错控制律设计。

2 改进的积分反演容错控制律设计

反演控制是针对非线性系统的控制方法，基本思想为：先将整个系统分解成多个子系统，再针对每一个子系统进行控制律设计，通过一系列子系统的虚拟信号以递归的方式得到控制信号，递归的每一步只需要处理一个相对简单的误差系统，可以较灵活地选择控制信号[15]。

传统反演法虽然能够实现对UAV非线性系统的稳定控制，但是当存在干扰和执行器失效故障的时候，传统反演法不具备抗干扰和容错能力，无法实现对指令信号的稳定准确跟踪。为了改善传统反演法的稳态性能和容错性能，将跟踪误差的积分引入到反演控制律的设计中，实现包容干扰和执行器失效故障的UAV容错控制[16-17]。积分反演容错控制律虽然能够实现包容干扰和执行器失效故障的UAV容错控制，但是控制律中的控制系数决定了UAV系统的响应时间和稳定时间等动态性能。为了改善积分反演法的动态性能，针对控制系数进行动态设计，使积分反演容错控制律能够快速包容干扰和执行器故障，迅速消除跟踪误差，稳定准确跟踪指令信号。

本文分别针对四旋翼UAV的高度回路、滚转回路、俯仰回路和偏航回路设计了改进积分反演容错控制律，通过在传统反演法中引入跟踪误差的积分项来改善UAV系统的稳态性能和容错性能，通过在积分反演法中引入动态控制因子来改善UAV系统的动态性能，最终实现包容干扰和执行器故障的UAV容错控制。容错控制系统结构如图2所示。

图2 容错控制系统结构

2.1 高度回路控制律设计

由式(6)可得高度回路故障方程为：

(7)

针对式(7)进行高度回路的积分反演容错控制律设计。

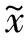
(8)

(9)

考虑如下Lyapunov函数：

(10)

式中：a1>0。对式(10)求导可得：

(11)

根据反演法的设计思路，将虚拟控制指令信号x2d设计为：

(12)

式中：c1>0。进一步可以得到：

(13)

由Lyapunov稳定性定理可以得到，控制系统渐进稳定。

(14)

则可以得到：

(15)

(16)

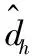
(17)

考虑如下Lyapunov函数：

(18)

式中：a2>0。对式(18)求导，并将式(7)和式(15)代入可得：

(19)

则设计积分反演容错控制律为：

(20)

式中：c2>0。进一步可以得到：

(21)

由Lyapunov稳定性定理可以得到，高度回路渐进稳定，可以稳定跟踪高度指令信号。

步骤3式(20)中的控制系数决定了UAV高度回路的响应时间和稳定时间等动态性能，为了进一步改善高度控制系统的动态性能，提高系统对执行器故障的容错性能，对式(20)中的系数进行动态设计。

将式(12)代入式(14)可得：

(22)

将式(22)代入式(20)可得：

(23)

(24)

(25)

(26)

(27)

式中：γ>2。则高度回路的改进反演容错控制律可以设计为：

(28)

2.2 滚转回路控制律设计

滚转回路控制律设计过程与高度回路类似，直接给出控制律如下：

(29)

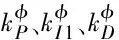
2.3 俯仰回路控制律设计

俯仰回路控制律设计过程与高度回路类似，直接给出控制律如下：

(30)

2.4 偏航回路控制律设计

偏航回路控制律设计过程与高度回路类似，直接给出控制律如式(31)所示。

(31)

针对四旋翼UAV的高度回路、滚转回路、俯仰回路和偏航回路设计了改进积分反演容错控制律，在控制律中引入了动态因子，改善控制系统的动态性能和稳态性能，实现包容执行器故障和干扰的容错控制。

3 仿真实验与结果分析

为了验证本文方法的优越性，对本文所设计的改进积分反演容错控制方法进行MATLAB/Simulink仿真，并分别与文献[15]中的反演控制律、文献[16]中的积分反演控制律得到的响应曲线进行对比。四旋翼UAV的模型参数如表1所示。

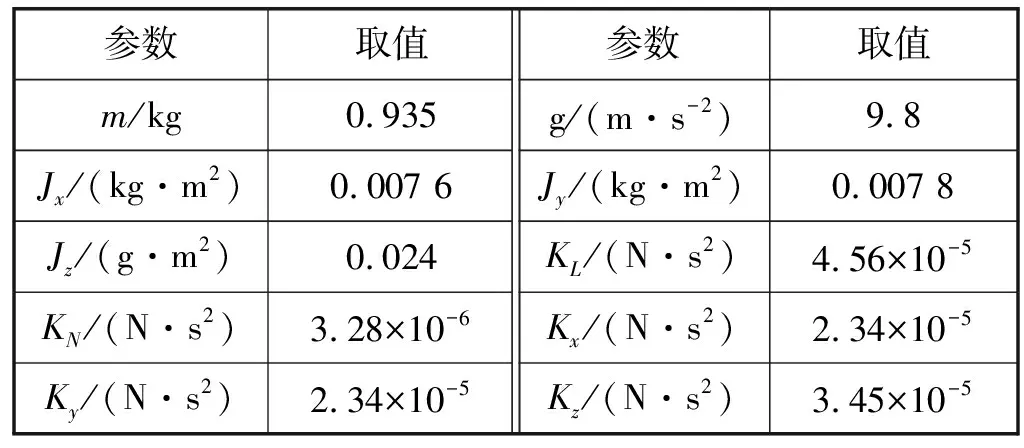
表1 四旋翼UAV模型参数

整个仿真时间为30 s，设定四旋翼UAV的初始状态为：h=0 m,φ=0°,θ=0°,ψ=0°。状态指令信号为：hd=3 m，φd=5°，θd=8°，ψd=10°。设定干扰dh=sin(0.5t)，dφ=cos(0.2t)+tan(0.3t)，dθ=0.8t，dψ=0.3t2。设定执行器故障为：t=5 s时，旋翼执行器1发生λ1=0.65的失效故障；t=10 s时，旋翼执行器2发生λ2=0.7的失效故障；t=15 s时，旋翼执行器3发生λ3=0.6的失效故障；t=20 s时，旋翼执行器4发生λ4=0.75的失效故障。不同的控制律在高度回路得到的仿真结果如图3所示。其中：实线为指令信号；长短虚线为文献[15]的响应曲线；短虚线为文献[16]的响应曲线；长虚线为本文方法控制律的响应曲线。

图3 高度回路仿真结果

可以看出：在文献[15]中一般反演控制律作用下，UAV在7 s时才能大致跟踪指令信号，并且当故障发生时，跟踪曲线会在指令信号附近剧烈振荡，振荡频率和振荡幅度都比较大，同时随着四个旋翼执行器失效故障的依次发生，跟踪曲线的振荡幅度也在逐渐增大。可以看出，一般反演控制律的稳态性能和动态性能都比较差，对执行器故障没有容错能力；在文献[16]中积分反演控制律的作用下，UAV在4 s时能够稳定跟踪指令信号，当故障发生时，跟踪曲线会发生-0.6 m～0.6 m的小幅振荡，并且在2 s后能够重新稳定跟踪指令信号。与文献[15]一般反演控制律相比，体现出此方法具有较好的动态性能和稳态性能，同时对执行器故障具有容错能力，突出了在一般反演法中引入误差积分项对于UAV容错控制的改善作用；在本文所设计的改进积分反演容错控制律的作用下，UAV在2 s时能够稳定跟踪指令信号，当故障发生时，跟踪曲线会发生-0.3 m～0.3 m的小幅振荡，并且在1 s内能够重新稳定跟踪指令信号，与文献[15]的一般反演控制律和文献[16]的积分反演控制律相比，体现出本文方法具有非常好的动态性能和稳态性能，同时对执行器故障具有良好的容错能力，说明了在积分反演法中引入动态因子对于UAV容错控制具有很好的改善作用。

同理，得到滚转回路、俯仰回路和偏航回路的仿真结果如图4、图5和图6所示。其中：实线为指令信号；长短虚线为文献[15]的响应曲线；短虚线为文献[16]的响应曲线；长虚线为本文方法控制律的响应曲线。

图4 滚转回路仿真结果

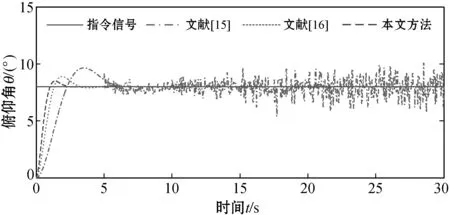
图5 俯仰回路仿真结果

图6 偏航回路仿真结果

通过对滚转回路、俯仰回路和偏航回路的仿真，进一步验证了本文所设计的改进积分反演容错控制律具有较好的动态性能、稳态性能和容错性能，能够快速、准确跟踪指令信号，从而验证了误差积分项和动态因子对于UAV容错控制系统具有较好的改善作用。

4 结 语

由于四旋翼UAV的执行器属于易损的机械部件，在高频的转动和复杂的环境下容易引起老化，当执行器发生故障时会对飞行器的安全稳定飞行造成严重的影响。通过对四旋翼UAV动力学模型进行分析，将其分解成高度、滚转、俯仰和偏航四个回路，在反演容错控制的基础上加入了误差积分和动态因子进行了改进，并将其应用在四个回路的控制律的设计中，有效改善了控制系统的动态性能和稳态性能。最后，在MATLAB/Simulink环境下进行了仿真和对比实验，验证了本文方法可以有效降低系统的稳态误差，提高容错性能，较其他文献的控制方法具有更快速的响应和更准确的跟踪精度，在发生执行器故障和干扰时能够保障四旋翼UAV的安全稳定飞行。