广义(2+1)维Boussinesq方程的初值扰动lump解和怪波解及动力学局域激发模式

康晓蓉 鲜大权 鲜骊珠

(1.西南科技大学数理学院 四川绵阳 621010；2.成都理工大学中英合作办学 成都 610059)

非线性现象在等离子体物理、固体物理、流体力学及化学动力学等科学和工程领域广泛存在，寻求这类非线性方程的精确解是理解这些复杂非线性物理现象的重要科学途径。Boussinesq方程是Boussinesq于1871年导出的非线性浅水波模型[1]，可以用于描绘浅水波、等离子体、非线性晶格等众多物理现象，模拟浅水非线性波相互作用、波流相互作用等[2-3]。随着这类模型应用的日益增加，相关研究不断深入，有了各种改进的Boussinesq方程，其中广义Boussinesq方程是重力波在地球表面传播的数学模型，是模拟波浪在海岸和海洋地区传播的有效科学工具。

本文研究如下形式的广义(2+1)维Boussinesq 方程[4]：

utt+α(u2)xx+βuxxxx+γuxx-uyy=0

(1)

其中：u=u(x,y,t)；α,β和γ均是任意实数。当α,β和γ取不同的值时,方程(1)可化为(1+1)维的Boussinesq方程和Benjamin-Ono方程[5-6]以及(2+1)维的Benjamin-Ono方程和Boussinesq方程[7-8]。

方程(1)的已有研究成果包括高阶呼吸波和lump解[4]、呼吸波解和一阶怪波解[9-10]、当α=3β或α=γ=-1,β=-3时的一阶lump解[11]、复怪波解[12]等。作为一个高维非线性数学物理模型，其动力学内涵是很丰富的，可用研究方法很多[13-15]。本文应用初值扰动双线性法研究该模型的lump解和怪波解的初值扰动行为。首先寻求方程的初值扰动双线性方程，再通过函数拟设法求解初值扰动双线性方程得到方程(1)的初值扰动lump解和扰动怪波解，最后应用计算机数值图像技术分析方程lump解的初值扰动行为局域激发模式。

1 方程(1)的初值扰动双线性结构

依据Painleve分析思想[16],选择方程(1)的初值扰动变换如下：

(2)

其中u0是方程(1)的初始常数解。

将式(2)代入方程(1),方程(1)化为如下带初值u0扰动的Hirota双线性形式[17-18]：

(3)

(4)

2 方程(1)的初值扰动lump解

为得到方程(1)的初值扰动lump解，取拟设函数φ为如下形式[19]：

(5)

其中，k0,ai,bi,ci,di(i=1,2)是待定参数，aibici≠0。将式(5)代入方程(3)并取积分常数B=0,可得关于待定参数的非线性超定代数方程组：

(6)

上述方程组有解：

(7)

u1=u0+

(8)

3 方程(1)的初值扰动怪波解

为得到方程(1)的初值扰动怪波解，对函数φ取如下拟设[20]：

φ2=a1t+b1x+c1y+d1+k1eη+k2e-η

(9)

其中：η=a2t+b2x+c2y+d2；ki,ai,bi,ci,di(i=1,2)为待定实数。将式(9)代入方程(3),取积分常数B及各次幂enη的系数为0,得到待定参数满足的非线性超定代数方程组：

(10)

上述方程组的解为：

(11)

令d1=d2=0,将式(11)代入式(9)，有:

(12)

其中η=a2t+b2x+θy。

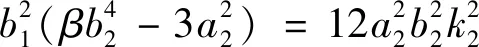
(13)

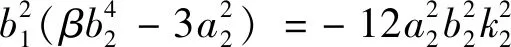
(14)

将式(13)和式(14)分别代入式(2),得方程(1)的两个初值扰动怪波解如下：

(15)

(16)

4 方程(1)初值扰动解的局域激发模式

本节作出方程(1)的初值扰动lump解u1在以下6种参数环境下的局域激发模式(见图1-图6，左为三维波面结构，右为等高线)。

(1)当a1=1,b1=1,d1=1,β=3,α=1,u0=-2,y=x时，记u1=u1a，u1a的局域激发模式如图1所示。

图1 u1a 的局域激发模式Fig.1 Local excitation mode of u1a

(2)当a1=1,b1=1,d1=1，β=3,α=-1,u0=2,y=x时，记u1=u1b，u1b的局域激发模式如图2所示。

图2 u1b 的局域激发模式Fig.2 Local excitation mode of u1b

(3)当a1=1,b1=1,d1=1,β=3，α=1,u0=-2,y=t时，记u1=u1c，u1c的局域激发模式如图3所示。

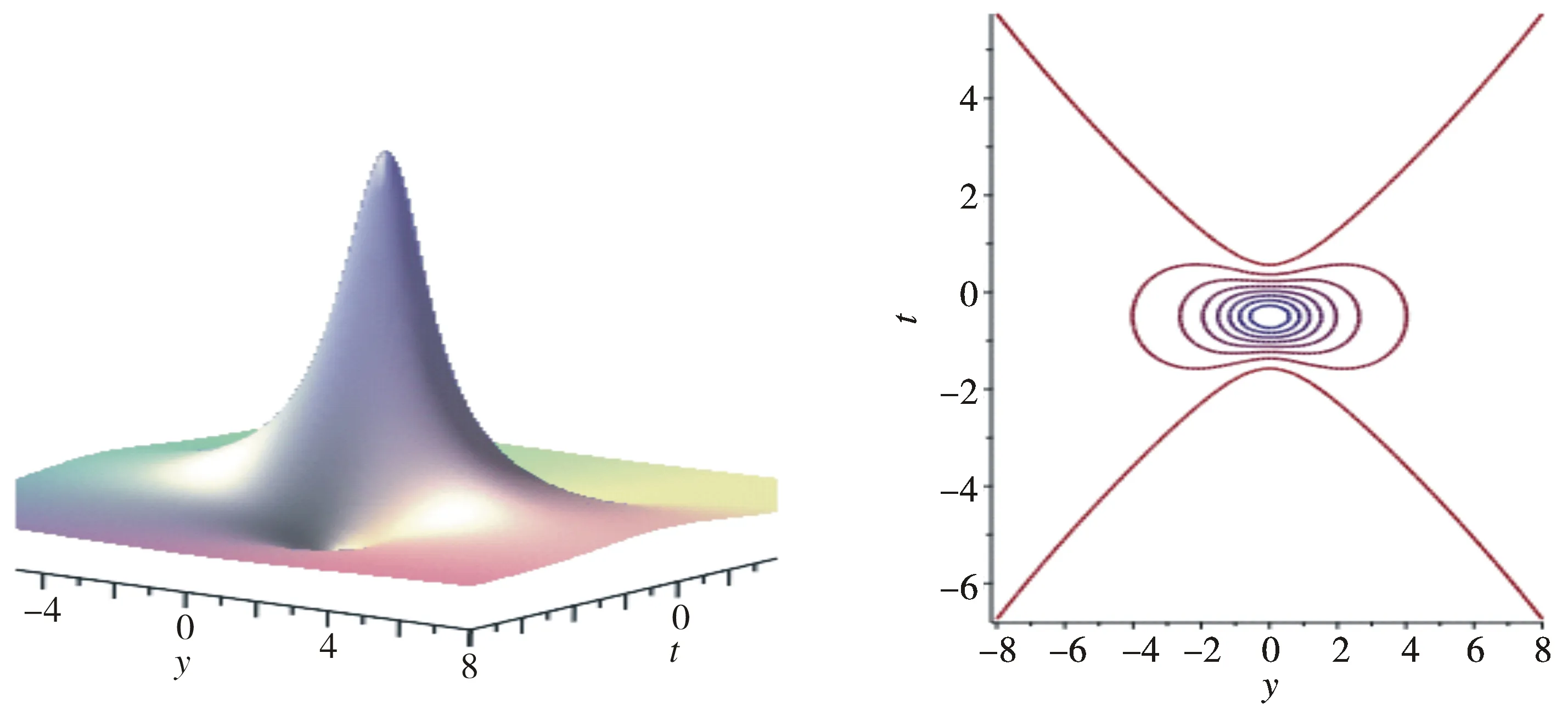
图3 u1c 的局域激发模式Fig.3 Local excitation mode of u1c

(4)当a1=1,b1=1,d1=1,β=3，α=-1,u0=2,y=t时，记u1=u1d，u1d的局域激发模式如图4所示。

图4 u1d 的局域激发模式Fig.4 Local excitation mode of u1d

(5)当a1=1,b1=1,d1=1,β=3，α=1,u0=-2,x=t时，记u1=u1e，u1e的局域激发模式如图5所示。

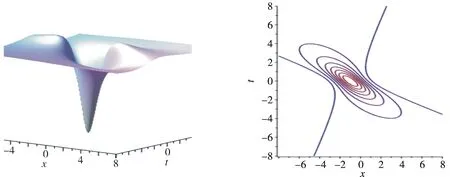
图5 u1e 的局域激发模式Fig.5 Local excitation mode of u1e

(6) 当a1=1,b1=1,d1=1，β=3,α=-1,u0=2,x=t时，记u1=u1f，u1f的局域激发模式如图6所示。

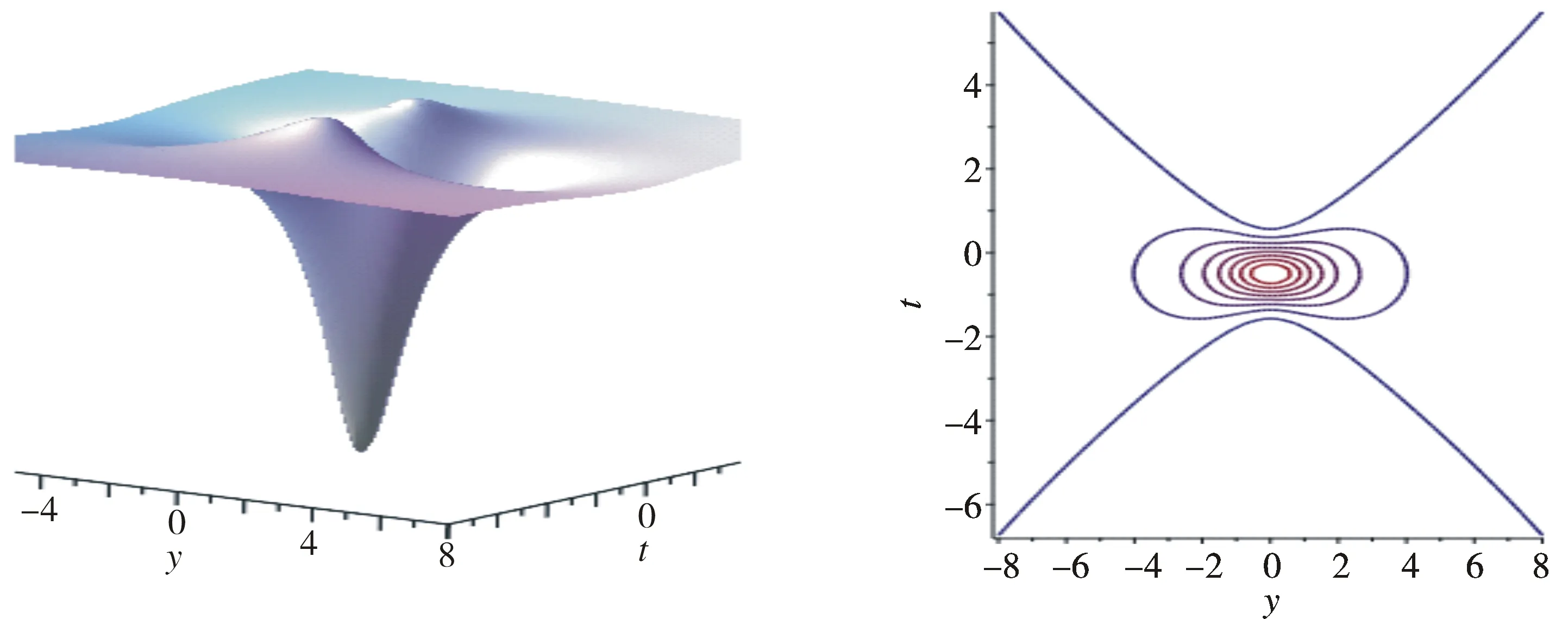
图6 u1f 的局域激发模式Fig.6 Local excitation mode of u1f

5 结论

利用双线性方法和拟设函数法研究广义(2+1)维 Boussinesq方程，通过初值扰动双线性法获得方程的初值扰动双线性结构方程，应用拟设函数法得到了方程的初值扰动lump解和怪波解及其初值扰动的分岔点，给出了初值扰动lump解在6种参数环境下的局域激发模式。本文所用研究方法和所得的解析结果丰富了Boussinesq方程的可积意义和动力学内涵。