一类高维波动方程和热传导方程Cauchy问题的简易解法
2022-07-12蒋思杨陕西师范大学数学与统计学院陕西西安710119
◎乔 雨 匡 超 蒋思杨(陕西师范大学数学与统计学院,陕西 西安 710119)
1 引 言
偏微分方程起初源于对物理与几何问题的研究,用来描述诸如振动弦与流体等物体的机械行为.现今在诸多数学分支,例如调和分析、泛函分析、微分几何与指标定理等领域,偏微分方程都被广泛地研究和应用.在本科阶段的课程中,偏微分方程主要是学习波动方程、热传导方程与位势方程的求解方法.其中波动方程和热传导方程,通常用Poisson公式和Poisson积分进行求解,但计算较为复杂.叠加原理在微分方程的求解中起到了非常重要的作用.在常微分方程中,非齐次线性常微分方程的解可以分解为对应的齐次方程的通解和一个特解之和.同样,叠加原理对于(线性)偏微分方程的求解也很重要,在许多非齐次边界条件的问题中也有着广泛的应用.本文旨在探索应用叠加原理简化一类问题求解步骤的方法,可以在教学过程中加深学生对叠加原理的认识与理解.
本文首先讨论了在齐次情况下,利用叠加原理与达朗贝尔公式对一类高维波动方程Cauchy问题进行降维的方法.之后根据齐次化原理讨论了非齐次情况下的降维方法.最后讨论利用类似方法对一类热传导方程的Cauchy问题进行求解.
2 齐次高维波动方程的Cauchy问题
对于齐次高维波动方程的Cauchy问题:
(2.1)
我们考虑在什么条件下可将上述方程拆解为如下三个一维方程:
(t>0,(x,y,z)∈R3)
(2.2)
(t>0,(x,y,z)∈R3)
(2.3)
(t>0,(x,y,z)∈R3)
(2.4)
这样拆解的优点是方程(2.2)~(2.4)是一维方程.而我们已经知道一维波动方程可采用达朗贝尔公式进行求解.
引理1(达朗贝尔公式) 一维齐次波动方程:
的解为:
对于二维以上的情况,下述定理给出了一个充分条件,使得方程(2.1)的求解可转化为方程(2.2)~(2.4)的求解.
定理1 (叠加原理)若齐次高维波动方程(2.1)满足下述条件:
(1)叠加关系:φ(x,y,z)=φ1(x,y,z)+φ2(x,y,z)+φ3(x,y,z),ψ(x,y,z)=ψ1(x,y,z)+ψ2(x,y,z)+ψ3(x,y,z).
(2)线性关系:φ1(x,y,z),ψ1(x,y,z)关于y,z线性;φ2(x,y,z),ψ2(x,y,z)关于x,z线性;φ3(x,y,z),ψ3(x,y,z)关于x,y线性.
则方程(2.1)的解为方程(2.2)~(2.4)的解之和.
证明:只需验证u(x,y,z,t)=u1(x,y,z,t)+u2(x,y,z,t)+u3(x,y,z,t)是方程(2.4)的解即可.对于初值条件显然满足;对于方程来说:utt=u1tt+u2tt+u3tt,且φ1(x,y,z),ψ1(x,y,z)关于y,z是线性的,根据引理1,则u1(x,y,z,t)关于y,z是线性的;同理可得φ2(x,y,z),ψ2(x,y,z)关于x,z是线性的,则u2(x,y,z,t)关于x,z是线性的;φ3(x,y,z),ψ3(x,y,z)关于x,y是线性的,则u3(x,y,z,t)关于x,y是线性的.故uxx=u1xx,uyy=u2yy,uzz=u3zz,utt=u1tt+u2tt+u3tt=a2(u1xx+u2yy+u3zz),所以utt=a2(uxx+uyy+uzz),即方程(2.4)的解为u(x,y,z,t)=u1(x,y,z,t)+u2(x,y,z,t)+u3(x,y,z,t).证毕.
例1求解下面波动方程的Cauchy问题:
解:由定理1,得方程的解等于下列三个方程解之和:
利用引理1可得这三个方程的解分别为
u1=x3+3a2xt2,u2=z(x2+a2t2),u3=0,
从而原方程的解u=u1+u2+u3,即u(x,y,z,t)=x3+x2z+a2t2z+3a2t2x.
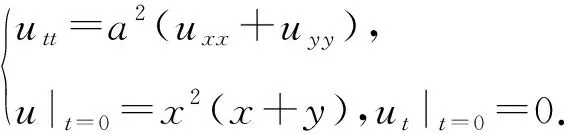

3 非齐次高维波动方程的Cauchy问题
对于非齐次的情况,我们首先根据齐次化原理给出一维非齐次波动方程的求解公式.
引理2 对于一维非齐次波动方程:
利用齐次化原理可得方程的解为
因此,对于非齐次高维波动方程的Cauchy问题
由定理1与引理2,我们可以将上述方程拆解为一维齐次方程与非齐次波动方程,从而由叠加原理求出该方程的解.下面给出几个具体例子.
例3求解下面非齐次方程的Cauchy问题:
解:该方程的解等于下列方程的解之和:
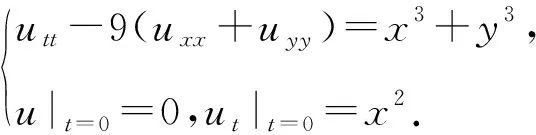
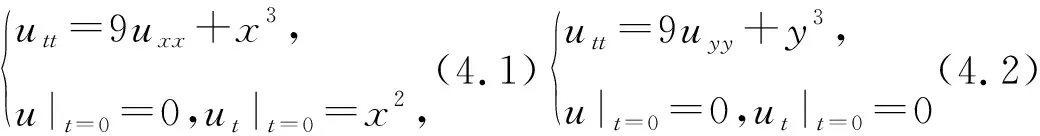
4 高维热传导方程的Cauchy问题
一维热传导方程的Cauchy问题可采用傅里叶变换得到求解公式.对于二维或更高维数的情形,尽管可利用高维傅里叶变换得出相应的求解公式,但是计算量较大.在下面的讨论中,我们将对一类具有特定条件的高维热传导方程的Cauchy问题,利用叠加原理将其拆分为一维情形进行求解.
引理3 一维热传导齐次方程:
的解为
类似于波动方程的情况,我们对热传导方程给出如下解的“乘积原理”.
定理2 对于二维热传导齐次方程:
若函数φ满足拆分条件φ(x,y)=φ1(x)φ2(y)(即φ1(x),φ2(y)分别与y,x无关),那么此Cauchy问题的解为u(x,y,t)=u1(x,t)u2(y,t),其中u1(x,t),u2(y,t)分别为如下两个方程的解:

所以u(x,y,t)=u1(x,t)u2(y,t)是定理2中方程的解.

解:根据定理2,该方程的解等于以下两个方程的解之积:

u1(x,t)=sinxe-t,u2(y,t)=sinye-t,
所以u(x,y,t)=sinxsinye-2t.
对于高维非齐次热传导方程的Cauchy问题,可利用齐次化原理转化为高维齐次热传导方程的Cauchy问题,若满足定理2的条件,则可转化为低维方程进行求解,这里不做过多阐述.
