一道解三角形综合题的解法探究
2022-07-12云南师范大学云南昆明650500
◎朱 琦(云南师范大学,云南 昆明 650500)
解三角形是高考的考点之一,近几年在题型上增加了结构不良试题,这在一定程度上增加了试题的开放性和难度.在解决解三角形问题的过程中,正弦定理和余弦定理是最常用的两个定理,它们将三角形的边、角有机地结合起来,实现了“边”和“角”的互化,从而为解三角形提供了强有力的支持.在新课标的指导下,人教A版新教材对正弦定理、余弦定理进行了调整,其中最突出的变化就是编排顺序,旧教材中将解三角形作为单独一章,而新教材中将正弦定理和余弦定理放在了平面向量这一章,作为平面向量的应用出现.这一改变突出了向量在解决几何问题上的简洁性和价值.在日常的训练中,与向量结合的解三角形问题也慢慢出现在学生的视野中,求解这类问题对于大多数学生来说都是难点.但进行深入探索之后也开发出了多种解法,下面笔者以一道解三角形的综合题为例,从多个角度探究其解法,以拓宽学生的思维.
试题呈现
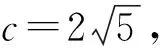
分析:该题是一道解三角形的综合题,考查了向量的运算、正余弦定理、三角形的面积等多个知识点,涉及转化与化归、数形结合等数学思想与方法.题干所给条件大多是隐性的,需要做进一步转化才能得出初步结论,因此对大多数学生来说,解题是困难的.在得到初步结论之后,最重要的是要能够画出相应图形,借助数形结合找到问题解决的突破口.而在解决解三角形问题时,最常用的方法是几何法和向量法,下面笔者从这两种方法切入,多角度地探究问题的解法.
解法探究
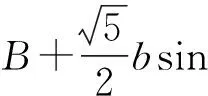
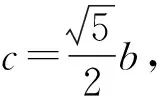
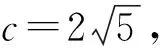

所以点O为△ABC的重心.
角度1:等面积法
分别取BC,AC,AB边的中点D,E,F,连接AD,BE,CF交于点O,如图1.
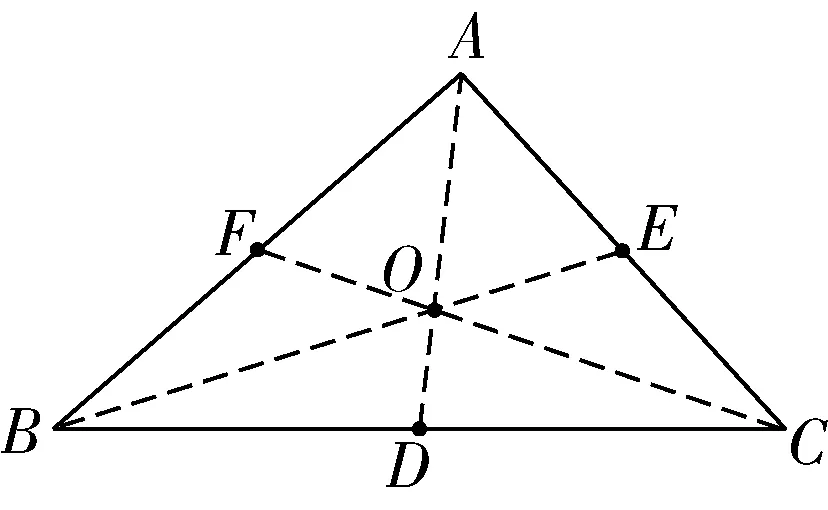
图1
由图1可以看出,因为点D为BC边的中点,所以S△ADB=S△ADC,即

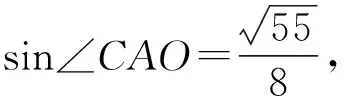


评析:等面积法是解决几何问题的一种很重要的方法,它以几何图形的面积公式为基础,建立起几何元素间的数量关系.利用等面积法解决数学问题,往往能达到事半功倍、出奇制胜的效果,上述解答过程就很好地说明了这一点.
角度2:利用正弦定理

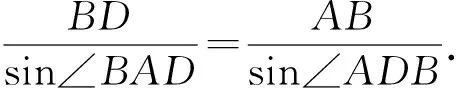


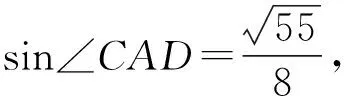


评析:通过多次应用正弦定理建立起三角形边角之间的数量关系,不失为一种巧妙的解法.值得注意的是,在解三角形问题中,要善于利用互补的两个角正弦值相等、余弦值互为相反数这一等量关系.
角度3:利用余弦定理
如图1所示,在△ABC中,∠ADB和∠ADC互补,
所以cos∠ADB=-cos∠ADC,即
化简得AD2+CD2=18,(1)


化简得
AD2-CD2+16=3AD,(2)
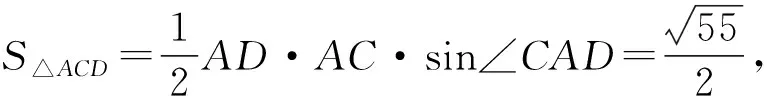

评析:上述解法利用互补的两个角余弦值互为相反数这一结论,建立起了AD和CD之间的等量关系.但是,仅仅只有这个关系还不能解答此题,还需要建立其他的等量关系,可以通过再次使用余弦定理,最终构建起方程组.
角度4:借助辅助线
在几何问题中,添加辅助线是问题解答的关键和难点,它可以将条件中隐含的图形性质体现出来,使得问题迎刃而解,下面是该题两种添加辅助线的方式.
(1)过点B作AC的平行线l,过点C作AB的平行线m,直线l和m交于点G,由此构造出平行四边形ABGC,如图2.
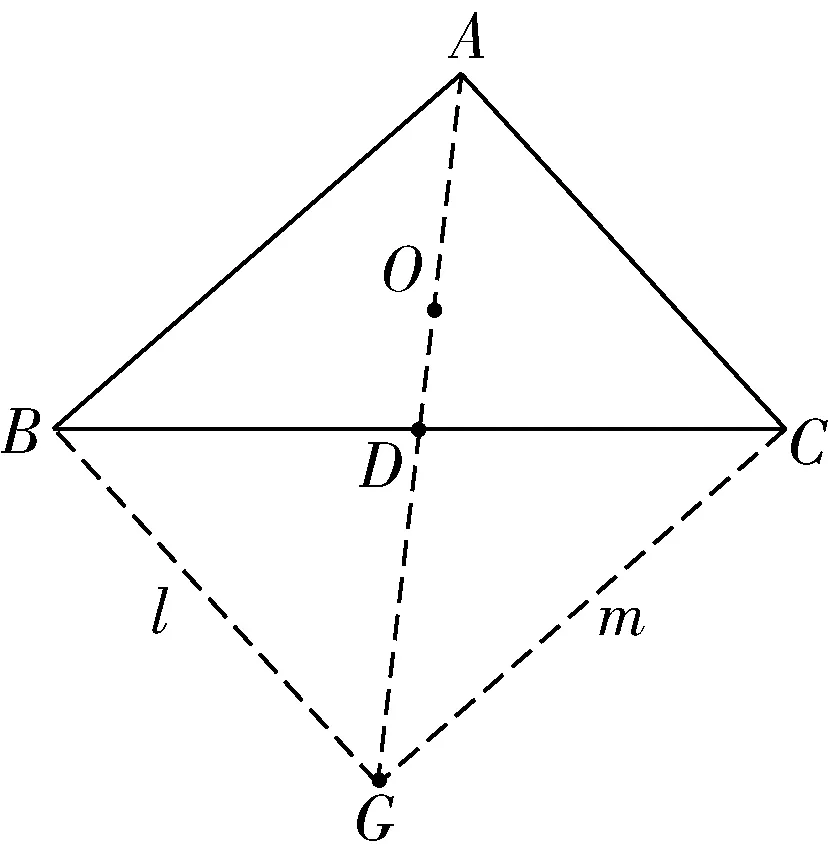
图2
因为四边形ABGC为平行四边形,
所以BG=AC=4,∠AGB=∠CAG.
在△AGB中,由余弦定理得



(2)过点O作OK∥AB,交AC于点K,如图3.

图3
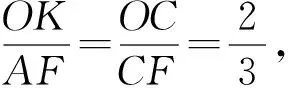
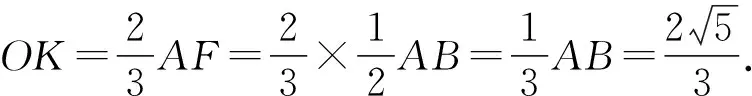
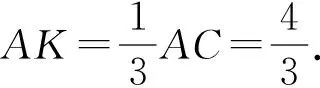
在△AOK中,由余弦定理得


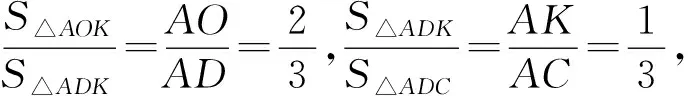


评析:第一种解法巧妙地运用了平行四边形的性质,将已知条件转移到同一个三角形中,从而便于使用正、余弦定理.第二种方法多依靠初中平面几何知识,通过构建相似三角形得出线段之间的数量关系.对比两种解法,解法1更为便捷和巧妙,解法2相对复杂.在几何问题中,辅助线的作用在于帮助学生快速解答问题,但是几何方法灵活多变,如何构建恰当的辅助线是一大难点,学生往往不能理解添加辅助线的本质目的,只能凭借记忆模仿或盲目尝试,因此,在很大程度上,问题的解决全凭运气.在日常教学中,师生共同归纳总结常见的几何模型,深刻理解模型的关键条件,有助于学生遇到类似问题时产生联想,从而有目的地添加辅助线,构建恰当的解题模型.
角度5:向量法
如图1所示,点D是BC边上的中点,

又因为点O是△ABC的重心,
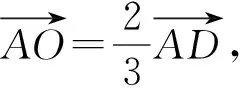

化简得
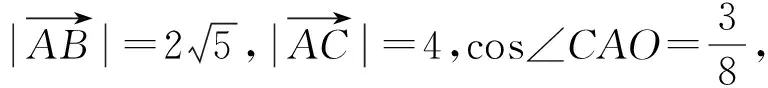
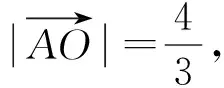
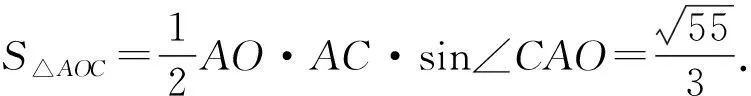
因为点O是△ABC的重心,
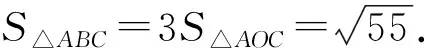
评析:向量既是代数研究对象,也是几何研究对象,是沟通代数和几何的桥梁.利用向量法解决几何问题可以把原来思辨的过程转化为较为简单的运算过程,降低了思考的难度,可以让学生感受到向量在解决某些平面几何问题中的优势.
教学反思
“一题多解”作为变式教学的一种,不仅在完善学生知识结构、发散思维等方面起着至关重要的作用,而且能够实现思维的分层教学,满足不同层次学生的需求.“一题多解”教学意味着课堂开放性强,这在一定程度上对教师的专业素养提出了挑战,下面针对“一题多解”教学提出三点策略.
1.精选解法,注重解法之间的联系
在“一题多解”教学中,解法不是越多越好,也不是越简洁越好,而是要有价值,有助于学生后续学习.这意味着教师首先要将问题研究透彻,精选解法,事先设计好教学环节,让课堂教学在问题的引导下有序进行,而不是将问题一味地丢给学生,让学生自主探索.其次是要注意解法之间的联系.目前很多教师存在罗列解法的习惯,过分追求解法的数量,忽视了解法之间的联系,导致学生对解法的本质认识不够深刻.
2.因材施教,给学生提供平等的数学学习机会
高中数学课标指出:人人都能获得良好的数学教育,不同的人在数学上得到不同的发展,这表明学生之间存在差异性,教师在教学时要看到这种差异并有针对性地进行教学.
在“一题多解”教学中,解法有易有难,有的学生可能只理解其中一种,而有的学生可能理解所有解法,但无论如何,学生总能找到最适合自己的那一种,这样一来便兼顾了不同层次学生的需求.因此,教师可以利用这种差异给不同学生创造数学学习机会.对于数学学困生,教师可以给其提供更多的课堂提问和板演的机会;对于数学学优生,教师要发挥好引导作用,鼓励他们从多个角度解决问题.
3.注重过程,培养学生的数学核心素养
美国数学教育家波利亚曾指出:解题的价值不是答案的本身,而在于弄清“是怎样想到这个解法的”“是什么促使你这样想、这样做的”,这表明了解题的目的不在于答案,而在于将知识和问题联系起来思考、分析、探索的数学思维过程.在传统教学过程中,学生的思维习惯于定向,而“一题多解”则是让学生克服定式思维,培养思维灵活性的有效途径.
因此,教师在日常教学中,要留意典型数学问题,适时开展“一题多解”训练,让学生亲自体验、感受、思考,在这个过程中对数学知识进行再创造,这样一来学生不仅巩固了数学知识,而且在思维上得到了训练,有效促进了学生数学核心素养的培养和提升.
