关于数学教师教育专业课程教学模式的思考
——以“中学数学解题”为例
2022-07-12陈少林衡阳师范学院湖南衡阳421002
◎陈少林 张 芸 陈 芳(衡阳师范学院,湖南 衡阳 421002)
1 引 言
教育部在《关于实施卓越教师培养计划2.0的意见》中指出:要在2035年之前培养和造就数以十万计的骨干教师、数以十万计的卓越教师、数以万计的教育家型教师.全国很多师范本科院校都是此卓越计划的参与者,作为师范本科院校的数学教师,我们将专注于中学数学卓越教师的培养.众所周知,培养一名卓越的中学数学教师是一个复杂的系统工程,而师范本科院校就是这个复杂系统工程的总设计师.成为一名卓越的中学数学教师,首先要有高尚的师德;其次要有高超的解决数学问题的能力和精湛的现代化教学艺术,最后还要具备一定深度的且与中学数学教学活动相关的教育学和心理学知识等.著名数学家P.R.Halmos认为:问题是数学的心脏,解决数学问题是数学家存在的理由.著名数学家G.Polya也曾指出:善于解题是掌握数学的标志.因此,要想培养出卓越的中学数学教师,除了高尚的师德,最重要的就是要解决如何培养数学类师范专业本科生的数学思维和高超的数学解题能力的问题.从教育学的角度来讲,要培养什么样的人才,课程是重要的实现途径之一.课程不仅是教育的桥梁,也是教学的灵魂.因此,我们要对教育进行改革,就必须对课程教学进行改革.类似于“中学数学解题”等实践类课程是高等师范院校数学教师教育课程体系中必不可少的一部分.本文主要讨论“中学数学解题”课程的教学改革问题.
2 教学模式的探究
数学类师范专业本科生和中学生的知识水平、理解能力、认知结构和接受新知识的能力都存在很大的差异,而且两者的培养目标也是不同的,因此教学方法应该也有很大的差异.虽然2001年教育部就印发了《普通高中研究性学习实施指南(试行)》,但是目前全国大多数中学数学教学模式仍然以教师讲授为主.要想在普通高中数学教学中普遍开展研究性学习,师资是关键.要培养具备这样素质的高中数学教师,高等师范院校有着义不容辞的责任.我们将以“中学数学解题”为载体,培养数学类师范专业本科生指导学生进行研究性学习的能力.下面本文将以“中学数学解题”为例,探讨如何在数学类师范专业本科生中开展研究性学习.
2.1 选择适当的问题进行深度解题教学
为了寻找合适的问题,教师应考虑如下几个方面的内容.首先,教师应该对授课对象的知识储备和认知水平有一定的了解.数学类师范专业本科生一般在大三第二学期才开设类似“中学数学解题”这样的课程,此时,他们几乎已学完了数学专业必修基础课程,大部分同学已具备了一定的数学专业素养.其次,教师要尽可能选择既具有中学数学背景,又与大学某个(或某些)数学课程的内容相联系的问题,那样更能提高学生进行研究性学习的兴趣.再次,教师选择的问题要有代表性且难度要适中.如果太难将不易激发学生的积极性,反之,如果太容易将没有任何挑战性,且研究性学习也将失去意义.一旦选定合适的问题之后,我们建议提前布置任务给学生,并允许他们查找相关资料以及组队研究.最后,教师应该至少从如下3个维度对学生进行引导.

表1 解题维度表
2.2 以2001年的一道全国理科数学高考题作为深度解题案例
问题1 已知m,n是正整数,且m

表2 要完成的任务
为了完成上述任务,我们将班级同学分成3人一组来进行探究(时间为30分钟).无论完成好坏,每组都必须汇报探究成果.对于问题1,从反馈的情况来看,大部分组都想到了利用函数的单调性进行证明,也有部分组想到了利用二项式定理展开来证明,还有极少数组想到了利用几何平均值不等式来证明.具体情况如下.
证明方法(一):
由二项式定理得:

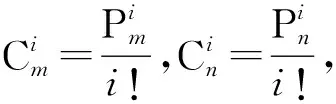
所以

因此
即(1+m)n>(1+n)m.问题1证毕.
也有个别组提出可以用几何平均值不等式去做.具体如下.
证明方法(二):
由几何平均值不等式得:
=(m+1)n.
而1+n≠1,且n>m,因此取不到等号.
于是有(1+m)n>(1+n)m,
所以,命题成立.
证明方法(三):


所以f′(x)<0.
即f(x)是单调递减的.
因此
以上三种证明方法相比较,第一种和第三种证明方法比较常规,然而第一种证明方法计算难度比较大;相比之下,第二种证明方法比较简洁,且用到的知识点很简单.虽然没有哪一组的同学能够同时想到这三种方法,但是他们通过反馈与交流都学会了这三种方法.遗憾的是,同学们对于问题1的其他任务完成得都不尽人意,因此我们有必要对此进行引导.
受问题1的证明方法(三)的启发,我们若将问题1中的整数改成有理数,则可得到如下结论.
2.3 命题1
设m,n∈N+且m≤n,则有
教师向同学们继续提问:能否用几何平均值不等式证明此命题?
很多同学能很快给出如下证明.
证明:只需证明右边,因为右边的证明完全类似.
由几何平均值不等式得:

2.4 命题2
设x1≤x2∈Q+,其中Q+表示正有理数集.则有
(1+x2)x1≤(1+x1)x2.
证明:存在m∈N+,使得mx1,mx2∈N+.
则原命题等价于
(1+x2)mx1≤(1+x1)mx2.
由几何平均值不等式得:
=(1+x1)mx2.
因此(1+x2)x1≤(1+x1)x2且当x1=x2时取等号.
特别要指出的是,我们利用有理数的稠密性可将命题2改写成如下形式.
2.5 命题3
设x1≤x2∈R+,则有
(1+x2)x1≤(1+x1)x2,其中R+表示正实数.
为了进一步巩固解题成果,我们下一步将继续讨论.笔者按照循序渐进的原则,设计了如下问题并要求学生对照表3进行深度解题.

表3 要完成的任务
2.6 案 例
问题2 设xk和yk都是正实数(k=1,…,n).证明:
同学们普遍觉得问题2要比问题1难,而且明显感到将问题1的证明方法直接迁移过来不是很实用.特别要指出的是:几乎所有组的同学都认为问题1的证明方法(三)对问题2已失效.但是稍加提示之后,很多同学很快就将问题1的证明方法(一)和(二)迁移过来.
提示:将乘积展开,再考虑用几何平均不等式.
有了这个提示之后,很多同学很快给出了证明方法(一).证明方法(一):

①
由几何平均值不等式得:
因此
将此不等式代入①式即可得要证明的结论.
提示:先将问题2中要证明的不等式的右边除以左边,然后再考虑可否利用几何平均值不等式来证明.
有了这个提示之后,大部分组的同学很快给出了如下证明.
证明方法(二):
原证命题等价于
由几何平均值不等式得:

因此
问题2证毕.
以上整个教学过程始终是以学生为中心,教师通过这样的协同探究过程激发学生解题的“元认知”,从而引领学生学习深度解题.这个分组探究的学习过程不仅激发了学生的解题兴趣,还拓展了学生的解题视野以及知识面.学生不仅学会了解题,还学会了如何深度解题.为了巩固学习成果,我们给每个小组布置布置了如下作业.
(1)按照问题1的任务模式,给出如下命题的证明:
设aij>0(i=1,…,n;j=1,…,k).则有
(2)要求每个同学对解题过程和解题方法进行回顾和再认识,将以上解题成果拓展的过程“精致化”,并建立相应的模型.
(3)以组为单位,自选主题(建议以历年的中、高考题为例),开展类似的深度解题活动并记录下来.每个人都必须分别标注自己在本次深度解题活动中的贡献并上交.(这是在该课程过程中给学生记平时分的主要依据.)
2.7 作业反馈
对上述案例进行分析,我们的主要目的不是让未来的中学数学教师学会解这种类型的题目,而是培养他们这种深度解题意识和习惯.他们一旦养成了深度解题习惯,受益的不仅是他们自己,还有他们将来要教的学生.对于教师来说,这样的深度解题教学模式尝试一次并不难,但要长期坚持下去却极具挑战性.因为这样的教学模式对教师提出了极高的要求,它不仅需要教师熟读教材,还需要教师具有广博的知识以及高超的深度解题能力.另外,这还需要教师对每一次课的内容的广度与深度进行精心设计.除此之外,教师需要在“中学数学解题”课程的教学过程中始终坚持以学生为中心,通过激发学生的“元认知”和提升学生的交流与协同意识来调动学生进行深度解题的积极性.

表4 作业反馈表
3 结 语
“中学数学解题”作为数学类师范专业本科生的一门重要的专业实践课,它有着自身的特点.教师通过这门课程的教学,加深学生对数学专业知识的理解并拓展学生的知识面,以及提高学生分析和解决数学问题的能力.为了实现此目标,教师需要在严格遵循“以学生为主体,教师为主导”的教学理念的前提下,选择恰当的教学模式.对于“中学数学解题”这门课程的教学,我们极力推荐基于研究性学习的深度解题教学模式.
