关于Cauchy收敛原理的几何解释在教学中的应用

◎姚卫红(上海交通大学数学科学学院，上海 200240)

一、内容介绍

关于微积分(高等数学)的教学，有很多经典的理论，例如实数的完备性六大定理，其中，确界存在定理、单调有界必有极限、区间套定理、聚点存在定理的几何意义非常明显.教师在教学中可以配合几何解释，加深同学们的印象.我认为比较有难度的是Cauchy收敛原理，它是六大定理中唯一一个充分必要的结论，对学生未来的学习意义重大.非数学专业的教学不见得要给出证明，但是可以讲一讲当初柯西是怎么想到的(这对培养和启发同学们的数学兴趣很有意义)，有什么划时代的意义，当初数学家的灵感来自哪里.一般来说，灵感是受到了几何意义的启发.所以，用几何的方法解释和证明定理的结论非常重要.我们知道，收敛的数列一定有界，有界不见得收敛.但是，有界而不收敛的数列一定不止一个聚点，换句话说，一定至少存在两个不同的聚点.这种情况肯定不是柯西列.

二、基本知识

定义1 设S为数轴上的点集，ξ为定点 (它可以属于S，也可以不属S)．ξ的任何邻域内都含有S中无穷多个点，则称ξ为点集S的一个聚点．

聚点概念的另两个等价定义如下：

定义1’ 对于点集S，若点ξ的任何ε邻域内都含有S中异于ξ的点，即U0(ξ;ε)∩S≠Φ，则称ξ为S的一个聚点．

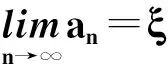
下面我们介绍魏尔斯特拉斯(Weierstrass)聚点定理．

定理 实轴上的任一有界无限点集S至少有一个聚点．

推论1 (致密性定理)有界数列必含有收敛子列．

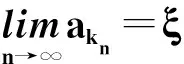
说明：若{an}中有无限多个相等的项，即存在完全相同的项组成的子序列，设为{akn}，则点a=akn也是数列{an}的聚点.

推论2 有界数列收敛当且仅当仅有一个聚点.

证明：因为数列收敛的充要条件是其任何子列都收敛到相同的值，而这个值一定是数学的聚点，所以，有界数列收敛当且仅当仅有一个聚点.

Cauchy收敛准则 —— 数列收敛的充要条件:

1.回顾基本列概念( 基本列亦称为Cauchy列)

基本列: 设{an}是一个数列，若对任意给定的ε>0，有一正整数N，当m,n>N时，有|an-am|<ε成立，则称{an}为基本列.

2.Cauchy收敛原理

定理 数列{an}收敛⟺{an}是Cauchy列.

一般来说，Cauchy收敛原理的证明是利用了致密性定理，为了方便读者阅读，我们这里给出教科书上数列的柯西收敛准则的证明(见下面的证明1).

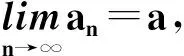
先证有界性，取ε=1，则∃N,n,m>N⟹|an-am|<1.特别地，n>N时,|an-aN+1|<1⟹|an|<|aN+1|+1.

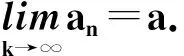
以上是国内外课本上的传统证明方法.在下面的证明2中，我们将采用几何解释法来证明数列的柯西收敛原理的充分性.我们的基本思路就是，根据推论2，有界数列收敛当且仅当仅有一个聚点.那么我们采用反证法，证明柯西列不可能有两个聚点，也就相当于证明了数列的柯西收敛原理的充分性.这样的证明方法几何特征比较明显，学生容易理解和接受，而且为未来学习上极限和下极限做好了铺垫(最大聚点就是上极限，最小聚点就是下极限).

证明2 (反证法)假设柯西列{an}不收敛，因为柯西列是有界数列，所以，{an}至少有两个不相同的聚点，设为A，B，不妨设A>B， 设{akn}及{aln}是数列{an}中两个不同的子列，分别以A，B为极限：

同理，∃N2∈N+，当n>N2时，

因此，当n>max{N1,N2} 时， 有

(1)

但因为{an}是柯西列，故∃N3∈N+，当n>N3时，有

(2)

结合(1)(2)，当n>max{N1,N2,N3}时， 有

矛盾.

下面我们给出以上这个证明的几何解释，有了这个几何解释，有两个聚点的数列一定不是柯西列便一目了然：

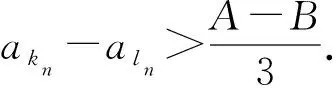
从上图可以看出，有两个聚点的数学列不可能是柯西列.

说明：

a.Cauchy收敛准则从理论上完全解决了数列极限的存在性问题.

b.Cauchy列也称为Cauchy条件，它反映这样的事实：原则上，收敛数列各项的值愈到后面，彼此愈接近，以至于充分后面的任何两项之差的绝对值可以小于预先给定的任意小正数.或者，形象地说，收敛数列的各项越到后面越是“挤”在一起，所以，直观上讲，有两个聚点的数列根本就不可能是Cauchy列.这就是我们本篇论文的主要思路.

c.Cauchy准则把ε-N定义中an与a的之差换成an与am之差.其好处在于我们无须知道数列收敛到什么(事实上也不见得事先就能够知道)，只要根据数列本身的特征就可以鉴别其敛散性.

3.Cauchy收敛准则的思想，可以用来理解Riemann的定积分的定义

众所周知，在教学中，定积分的定义(Riemann的定积分的定义)理解的难度相当大，它是数学分析和高等数学当中最难懂的定义.但是我们借鉴Cauchy收敛准则的思想，可以大大地弱化理解的难度.

我们首先来回顾一下Riemann的定积分的定义(见下面的定义1、定义2和定义3)

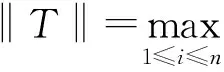
注：①由于Δχi≤‖T‖，i=1，2，…，n，因此‖T‖可用来反映[a，b]被分割的细密程度.

注：显然积分和既与分割T有关，又与所选取的点集{ξi}有关，有了上述两个定义，我们便可简洁地写出定积分的定义.

(3)

其中f称为被积函数，χ为积分变量，[a,b]为积分区间，a，b分别称为这个定积分的下限和上限.

以上定义1～定义3是定积分抽象概念的完整叙述.下面是与定积分概念的有关的几点补充注释.

表达定积分的极限形式：

(4)

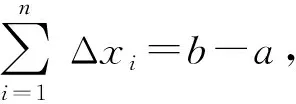
(5)

总之，理解这个问题的关键点在于把[a,b]的分割T看作限制函数f的自变量取值范围的量，类似于一致收敛定义中的δ，而不要将它看作一个变量.这样再来看黎曼的定积分的定义，就与一致连续的定义没有本质差异了.所以，定积分的定义也可以陈述为：

(3’)

其中f称为被积函数，x为积分变量，[a,b]为积分区间，a,b分别称为这个定积分的下限和上限.

这样叙述Riemann的定积分的定义，理解的难度大大降低.