浅议指向初中数学问题解决能力的教学设计——从一节数学课的磨课说起
2022-07-11高八民西藏山南市乃东区中学
高八民 西藏山南市乃东区中学
义务教育数学课程标准(2011版)》课程总目标中明确提出,通过义务教育阶段的数学学习,学生应能“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系,运用数学的思维方式进行思考,增强发现和提出问题的能力、分析和解决问题的能力”。这一基本理念在我区2021年初中学业水平考试规定中的命题要求中也做了明确规定:“考试命题要引导教师积极探索基于情境、问题导向、深度思维、高度参与的教育教学模式”。这就要求数学课堂教学在进行教学设计时不能仅仅考虑学生对知识本身的学习和理解,更要考虑到数学知识与现实情境和实际问题的联系,把指向问题解决能力培养的数学抽象、数学推理、数学建模等重要的核心素养融入到具体的教学设计中来,从现实问题中抽象出数学问题,用数学的方法予以解决,从而促进数学应用意识和创新意识的培养。
近期有幸观摩了一节“角平分线的性质应用之巧解面积问题”的数学公开课,系参加区域性优质课教学比赛的一次数学磨课,后来又得知授课教师在比赛中获得了一等奖的好成绩。当然,之所以选择这一课例作为载体进行深入分析的最主要原因是这堂课从教学导入、集体研学、应用启学和挑战拓学等教学环节均能够充分地体现授课教师关于数学课堂教学中问题解决能力培养的思路和设计。接下来文章将从问题解决的视角对这节课的教学设计进行分析探讨。
一、关注数学问题解决能力培养的教学导入
培养学生数学实际问题解决能力首先要让学生能够从生活中发现问题、提出问题,进而才可能达到分析和解决问题的目的,因此如何在教学导入的环节中,通过生活中的一件事或者一个具体的现实情境把问题引出来,从而让学生把这一问题抽象为数学问题,并能够联系已有知识做出初步解决问题的判断是关键。在这一点上有一个非智力因素也要引起重视,就是学生对实际问题的兴趣,数学活动如果一开始不能够激发学生的兴趣和注意力,就很难调动学生主动探索的积极性,引发学生对于数学问题的思考。
课例中(图1),教师从绝大多数学生熟悉的动画片熊大熊二的趣事入手,阐述故事情节“熊大熊二家门口,有一大片呈三角形状的森林,树林里长满了果子,熊大说‘熊二,俺们要在河边找一个点,使得从俺们家到达这点所在的直线可以平分果园面积,俺俩一人一半’”,引出实际问题“熊二:熊大,你说的俺不懂,谁能帮帮我呀?”这一设计主要表达的设计意图和理念是:一方面通过学生感兴趣的动画人物间的对话故事引出三角形平分面积的问题;另一方面通过这一问题让学生回忆起已学过的“中线分三角形面积”这一知识点并产生对于这一原理的初步理解,当然在老师的引导下,还可以归纳出一个结论:同高三角形的面积之比等于底边之比。从问题解决能力培养的角度来看,这一环节设计之巧妙在于能够通过动画角色的对话以故事的形式融入接近现实生活的实际问题来引发学生思考,更重要的是这一问题导入简化了把实际问题抽象为数学问题的难度,使得学生容易实现数学抽象,即“用数学的眼光观察现实世界”。

图1
二、体现数学问题解决能力培养的活动探究
从数学学科的发展过程来看,数学每前进一步都离不开严密的逻辑推理,数学的学习就是要重点培养逻辑推理,课程标准也明确指出“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等过程”,因此,在培养学生解决问题能力的数学教学过程中设置活动探究环节必不可少。课例中第二个教学环节“集体研学”最初的设计是“在△ABC 中,P 为BC上任意一点,探究△ABP与△ACP的面积之比(用线段比表示)”和“在△ABC中,AP平分∠BAC与BC交于点P,探究△ABP 与△ACP 的面积之比”两个问题,具体活动组织是学生独立思考两分钟后写出解答过程并进行同桌二人对学交流,教师巡视并邀请小老师上台讲解。在磨课后老师们更多地建议设计成“在△ABC 中,AP 平分∠BAC 与BC 交于点P,探究△ABP 与△ACP的面积之比(用线段比表示)”、“还可以怎么样表示?”和“在△ABC 中,P 为BC 上任意一点,探究△ABP与△ACP的面积之比”三个问题,活动组织不变。
通过前后两个设计的对比,第一种设计意图是在导入环节得出“同高三角形的面积之比等于底边之比”这一结论的基础之上直接展开应用归纳出普遍性结论,再用来解释对问题二的猜想和解释。这一设计更侧重于从认知心理学出发,通过像操练肌肉一样操练认知从而达到神经元结构的固化,通过高度相似的数学问题和类比简化数学推理,一定程度上使得探究活动更容易成功。第二种设计则主要是考虑到课题的主题是“角平分线的性质应用”,因此在导入环节得出“同高三角形的面积之比等于底边之比”的结论之后,通过问题串让学生拓展思维,主动探索得出面积的不同表达,通过同伴交流体会一题多解的解题思路,同时再由特殊到一般,探究的同时理解特殊条件下得出结论其适用范围具有局限性。这一设计可以让学生更好地经历“猜测-验证-归纳”的活动过程,在激发探究热情、促进合作交流方面也更加符合探究活动所要表达的意义,但从内容上无疑更适合学生基础较好的班级。
三、渗透数学问题解决能力培养的思想方法
学习不是简单的知识存储和输入,更是一个知识加工和输出的过程。在培养问题解决能力的数学教学过程中,必须渗透数学的方法和思想,比如由简单到复杂、由特殊到一般、“猜想、验证、归纳”、类比推理、分类讨论、数学模型等。课例之所以能够在优质课大赛中脱颖而出,笔者认为主要表现在两个方面:第一,教学案例通过由“特殊到一般”这一探究逻辑对中线和角平分线分三角形面积的情况引导学生探究,再推广到一般情况下的普遍规律,启发学生深刻理解角平分线的特殊性以及性质运用的灵活性(见图2)。第二,在“集体研学”环节之后的“挑战升级”和“思维百变”两个知识的深化拓展环节,课例设计了“角平分线分三角形情况下根据面积比求线段长”和“三角形三条角平分线分割三角形情况下,求大三角形面积”两个问题,这两个问题把方程思想、整体思想和转化思想渗透到解决问题之中,用解题的经验告诉学生问题解决往往是多个知识点的整合应用,除了基本知识、基本技能之外,基本的活动经验和基本数学思想也是数学学习所要领会的关键。

图2
四、建构数学问题解决能力培养的知识体系
建构主义学习理论认为,学习是学生主动建构知识的过程,教学应引导学生在原有的知识经验中通过有意义的问题情境主动构建新的知识经验,从而促进学生形成指引问题解决的知识体系和逻辑图式。课例在“反思感悟”环节,从数学知识、数学方法、数学思想三个方面让学生展开反思总结、感悟收获,同时突出角平分线作为研究问题的已知条件的特殊性以及对于问题解决思路拓展的灵活性,在这点上可以说基本上能够引导学生作为学习的主体朝着“用数学的眼光观察”、“用数学的思维思考”和“用数学的语言表达”三个要求迈进。
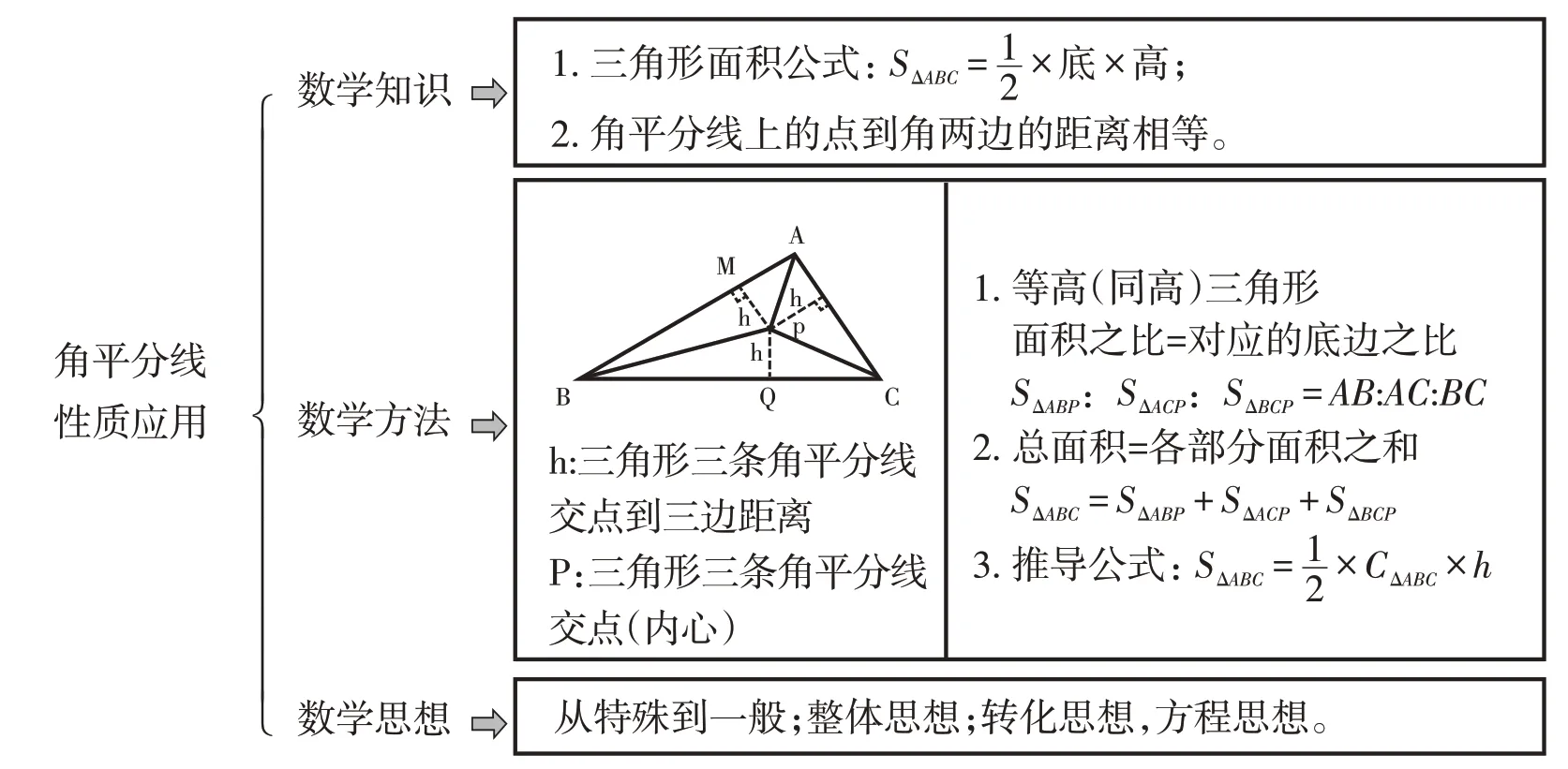
图3
尽管老师们在谈论数学教学的时候,都认可课堂教学是一个动态生成的过程,也认可教学生成是教学预设的必要补充,具有必然性。但也必须承认成功的、高效的数学课堂离不开精心预设,它更应成为动态生成的基础和起点。培育学生数学问题解决能力的教学设计更需要立足学生的学情和兴趣,通过能够激发学生兴趣点和注意力的问题把学生引入数学的探究活动中来,运用数学的方法展开严密的逻辑推理,并总结数学活动的经验和思想,梳理形成自己的数学知识体系,这点上还有待更多地通过观评课活动加以分析和反思。
