曲线线路参数对钢轨横向模态的影响
2022-07-11岳国栋董京王大志王立鼎蔡小勇洪嘉希
岳国栋 董京 王大志 王立鼎 蔡小勇 洪嘉希
1.沈阳建筑大学机械工程学院,沈阳 110168;2.大连理工大学机械工程学院,辽宁大连 116024;3.沈阳铁路信号有限责任公司,沈阳 110025
相较于直线线路,曲线线路承受较大的横向力。横向刚度较低,易造成轨道损伤,影响行车安全。模态是结构振动固有属性,经常用于钢轨健康监测。模态会受轨道参数的影响,因此有必要研究曲线线路参数对模态的影响规律。
国内外学者把曲线线路简化为多种力学模型,开展动力学特性研究。研究人员把钢轨中性层和曲率中心归为一个平面,把钢轨运动分为平面外振动和平面内振动两种形式。杜林林等[1-2]建立了离散点支撑曲线轨道平面内外弯扭耦合的频域解析模型,研究移动荷载速度、轨道半径、内外轨超高等对曲线轨梁垂向、横向、扭转变形动力学响应特性。王开云[3]采用Euler梁模型模拟离散点支承曲线线路,建立了曲线轨道轮轨动态相互作用性能分析模型,研究轨道结构振动对曲线轨道轮轨动态相互作用性能影响。刘卫丰等[4]把钢轨考虑为曲线Timoshenko 梁,建立离散支撑的曲线轨道解析模型,在轨头施加横向固定谐振荷载,研究扣件刚度、扣件阻尼、扣件间距和曲线半径对钢轨位移的动力学影响。雷晓燕等[5]通过建立数学模型,将无缝线路钢轨与轨道板简化为Euler 梁和Timoshenko 梁,仿真分析不同轨道参数对轨道结构高频频带的影响,指出两种梁模型结构计算结果差异主要集中在高频频带范围内,且Timoshenko 梁在高频处的适应性更好。赵江伟等[6]建立不同扣件参数下有限元模型,研究扣件类型和扣件刚度对曲线线路波磨影响,指出扣件刚度在特定范围内改变不影响自激振动对应的频率,且垂向刚度过小会加剧曲线线路波磨。上述研究均侧重在建立模型讨论轨道参数对某阶或某几阶模态的影响规律。大量模态试验显示,由于实际服役线路工况非常复杂,仅仅相隔几十米的两点,特定的某阶模态也有明显不同。仅研究轨道参数对特定阶模态的影响对工程应用的参考价值依然有限。
轨道是一个沿着特定方向延伸的周期性结构。边界条件为离散支撑的扣件、轨枕等结构,作为随机事件影响钢轨模态。由轨道参数改变引起的模态变化,能够反映轨道参数对轨道的影响程度。由于模态间相互独立,频率的变化值构成一组随机序列,依据大数定律,轨道参数对钢轨整体模态变化的影响具有稳定性。基于这种思想,本文通过建立曲线线路钢轨-扣件-轨道板三维有限元模型,分析曲线线路钢轨振动传输特性,研究扣件刚度、曲线半径、扣件间距等轨道参数对钢轨固有频率变化的影响规律。
1 曲线线路力学模型
1.1 有限元模型
采用ABAQUS 软件建立钢轨-扣件-轨道板三维实体模型。钢轨为CHN60轨,长度为20 m。扣件采用弹簧-阻尼器来模拟,建立三向弹簧并约束旋转自由度。钢轨一侧对称约束,一侧自由,如图1(a)所示。在对称约束处施加激励,并细化激励作用处网格,如图1(b)所示。采用正六面体C3D8R单元,钢轨网格种子大小为0.03 m,便于研究最高3 000 Hz 的频率;轨道板网格种子大小为0.05 m,以减少计算量。模型尺寸参照60 kg/m 无缝线路钢轨建立,扣件采用弹簧-阻尼单元模拟,考虑扣件的三向刚度和阻尼。根据文献[7-8]确定扣件垂向、横向及纵向的刚度及阻尼参数,轨道板采用混凝土Ⅲ型轨枕参数。
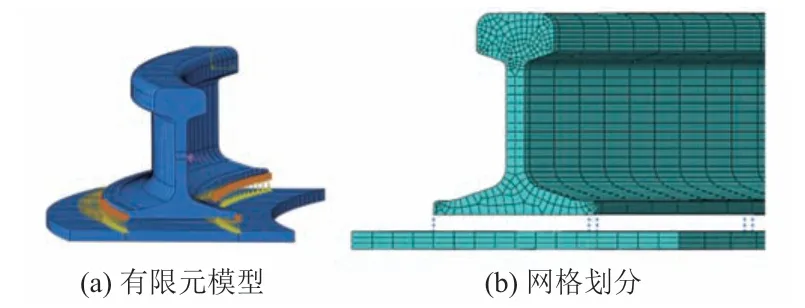
图1 钢轨有限元模型及网格划分
1.2 传输特性分析
振动衰减率是量化钢轨振动传递的重要指标,钢轨的传递特性取决于钢轨振动衰减量。依据欧洲标准 BS EN 15461∶2008+A1∶2010《Railway Applications-Noise Emission-Characterisation of the Dynamic Properties of Track Sections for Pass by Noise Measurements》,钢轨振动衰减率RD的计算式为
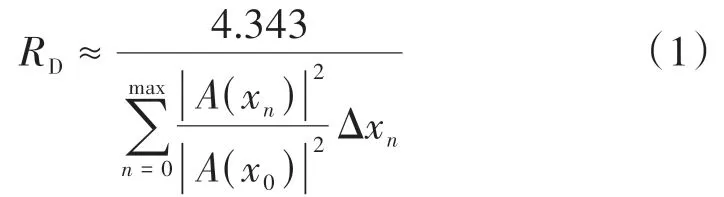
式中:A(xn)为激励点处施加荷载时n点的速度频响函数;A(x0)为激励点处施加荷载时激励点处的速度频响函数;Δxn为n点与激励点的距离。
利用式(1)绘制轨头、轨腰处以及轨底的振动衰减率曲线(图2),结果与文献[9-10]在1 000 Hz 内结论类似。由图2可知:在0 ~ 400 Hz、1 449 ~ 1 683 Hz、2 137 ~2 522 Hz 频带内,钢轨的振动衰减率较高,这是因为部分能量在扣件处被消耗,部分能量通过扣件向地基传播;轨头处的振动衰减率最大,其次为轨腰,轨底处的振动衰减率最小,这是因为轨头处起始振动能量较大,轨腰次之,轨底最小。由于0 ~400 Hz内存在振动衰减,模态会受到地基影响,3 000 Hz以上钢轨模态波长较短,不易识别,故将分析频带设置为500 ~3 000 Hz。
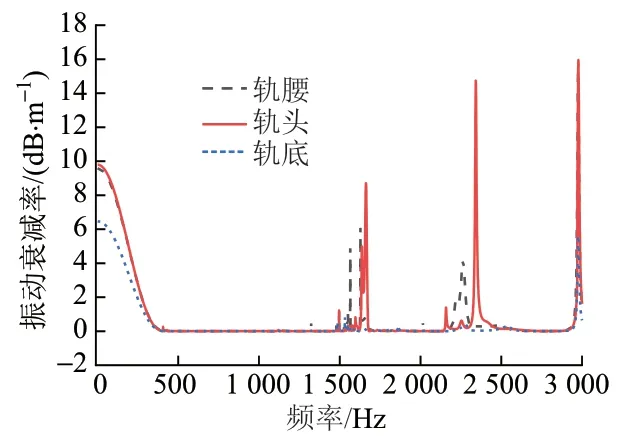
图2 钢轨不同位置振动衰减率
1.3 模型验证
由于激励能量、模态参与度等影响因素的存在,很难激发服役钢轨的全部模态。为获得可激发的模态,在服役钢轨上进行模态试验。在钢轨轨腰处布置3 个加速度传感器,在相邻跨度内选定5 个激励点,逐点多次激励,采集响应点处加速度值。试验现场为有砟无缝线路钢轨,为保证验证结果的准确性,有限元模型亦为无缝线路钢轨,且采用线性弹簧模拟扣件。试验平台如图3所示。
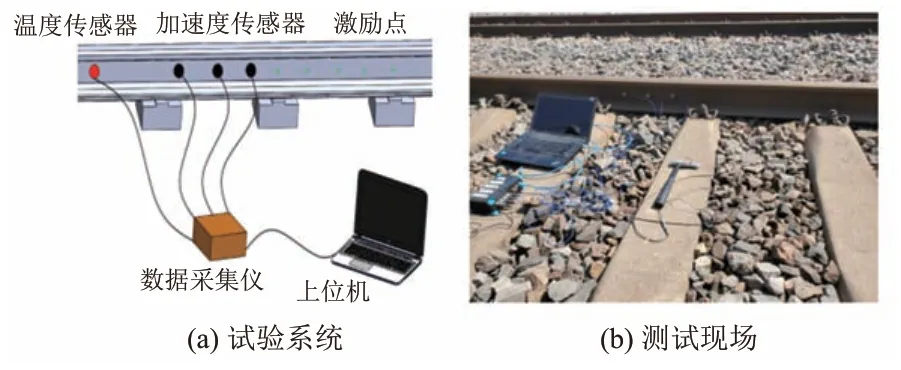
图3 试验平台
对采集的振动数据进行频域分析,求得频响函数,由频响函数提取钢轨的固有频率作为研究对象,共有21 阶频率。如图4 所示,试验频率与仿真模型提取的频率略有差异,最大误差比在3%以内,可认为仿真频率和试验频率具有很好的一致性。
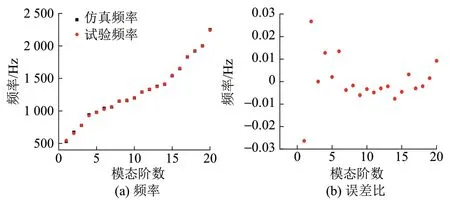
图4 试验频率与仿真频率对比
2 曲线线路振动特性分析
2.1 扣件刚度对振动特性影响分析
对扣件刚度不同的曲线线路进行谐响应分析。曲线线路半径取800 m,扣件间距取0.6 m,扣件刚度分别取5、10、15、20、25 kN/mm,依次编号为工况1—工况5,取工况3 为标准工况。不同扣件刚度下频率-加速度曲线见图5。提取各工况的钢轨固有频率f(ii=1 ~5),与标准工况下的钢轨固有频率作差,计算其频率变化值Δfi=f3-fi,并得出频率变化均值。频率变化值及频率变化均值随频率的变化曲线见图6。
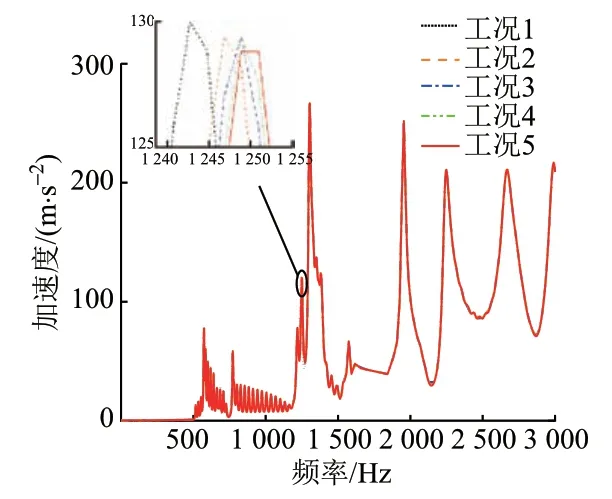
图5 不同扣件刚度下频率-加速度曲线

图6 不同扣件刚度下各阶频率变化值及频率变化均值
由图6(a)可知:当扣件刚度发生改变时,扣件刚度对钢轨各阶固有频率的影响在-4 ~8 Hz;在500 ~700 Hz、930 ~ 1 410 Hz、1 650 ~ 1 670 Hz 频带处各工况频率均存在较大的突变,对500 ~700 Hz 频带影响最为明显;在1 750 ~3 000 Hz 频带内,扣件刚度变化对钢轨的固有频率影响较小。
由图6(b)可知:对于扣件刚度小于标准扣件刚度的工况1、工况2,频率变化均值为正,为0 ~ 6 Hz,且随频率增加而呈下降趋势,分别趋近于1.08、0.22 Hz;对于扣件刚度大于标准扣件刚度的工况4、工况5,频率变化均值为负,为-4 ~0 Hz,且随频率增加而呈上升趋势,分别趋近于-0.25、-0.46 Hz。
以5 阶低频和5 阶高频为例,其各阶频率随扣件刚度的变化曲线见图7。对各曲线进行拟合,可知频率随扣件刚度呈线性变化,线性相关系数均大于0.95。各拟合直线的斜率可认为是每阶频率对扣件刚度的敏感性。
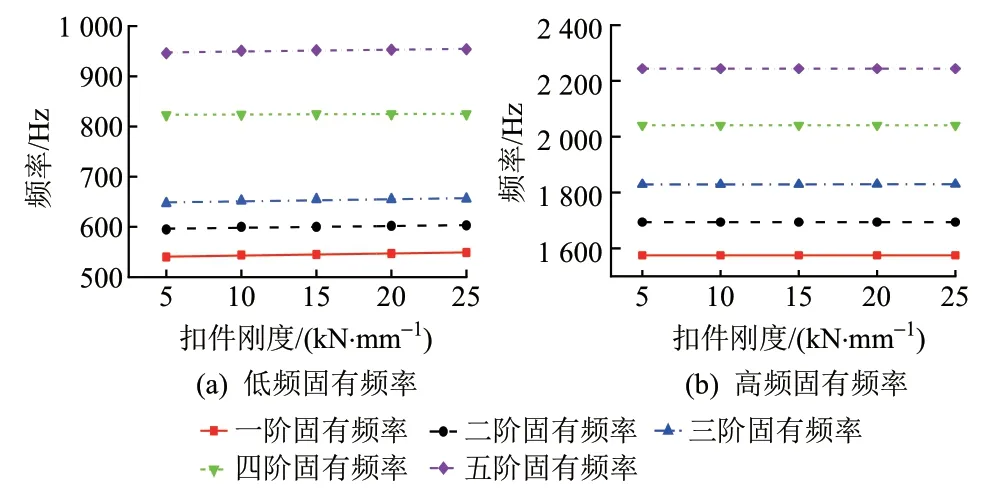
图7 固有频率随扣件刚度的变化曲线
获取所有研究频率对扣件刚度的敏感性,见图8。可知:在500 ~1 000 Hz 频带内,频率对扣件的敏感性较高,在0.5 ~2.1 Hz/(kN/mm);其余频带内的敏感性均较低,其中1 500 ~3 000 Hz频带内频率对扣件的敏感性为0 ~0.5 Hz/(kN/mm)。
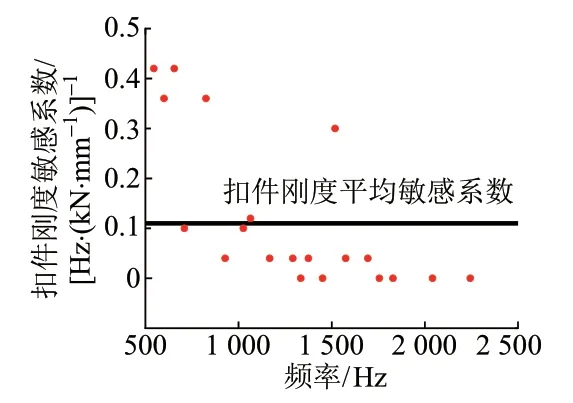
图8 各阶固有频率对扣件刚度的敏感性
2.2 曲线半径对振动特性影响分析
对不同半径的曲线线路进行谐响应分析。扣件刚度取15 kN/mm,扣件间距取0.6 m,曲线半径分别取400、600、800、1 000 m,依次编号为工况6—工况9,取工况8 为标准工况。通过谐响应分析,获取不同工况下的频率加速度曲线,提取各工况的钢轨固有频率fj(j= 6 ~9),与标准工况下的钢轨固有频率f8作差,计算其频率变化值Δfj=f8-fj,并得出频率变化均值。频率变化值及频率变化均值随频率的变化曲线见图9。
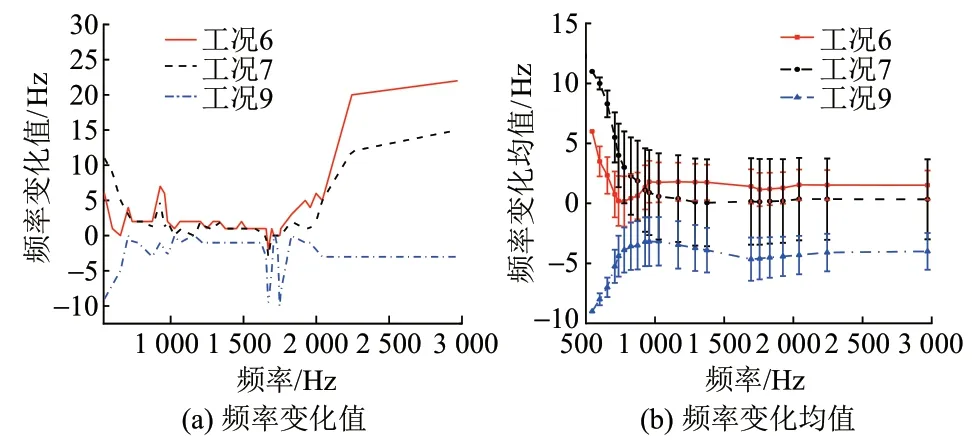
图9 不同曲线半径下各阶频率变化值及变化均值
由图9(a)可知:曲线半径使钢轨固有频率变化值在-9 ~ 12 Hz;在 500 ~ 704 Hz、850 ~ 960 Hz、1 650 ~1 800 Hz频带内,频率有较大突变,在1 650 ~1 800 Hz频带内受曲线半径影响最明显。
由图9(b)可知:对于曲线半径小于标准曲线半径的工况 6、工况7,频率变化均值为正,为 0 ~11 Hz,且随频率增加呈下降趋势,分别趋近于1.50、0.34 Hz;对于曲线半径大于标准曲线半径的工况9,频率变化均值为负,为-9 ~0 Hz,且随频率增加呈上升趋势,趋近于-4 Hz。
以5 阶低频和5 阶高频为例,其各阶频率随曲线半径的变化曲线见图10。对各曲线进行拟合,可知频率随曲线半径呈线性变化,线性相关系数均大于0.95。随着曲线半径增加,每阶频率也随之增加,二者正相关。获取每阶频率对曲线半径的敏感性系数,见图11。可知,除个别频率外,固有频率的曲线半径敏感系数大致相等,约为0.01 Hz/mm。
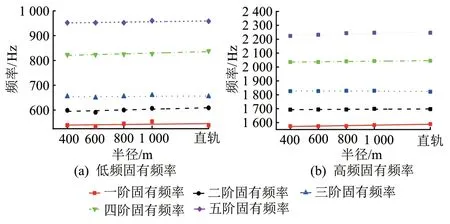
图10 固有频率随曲线半径变化曲线
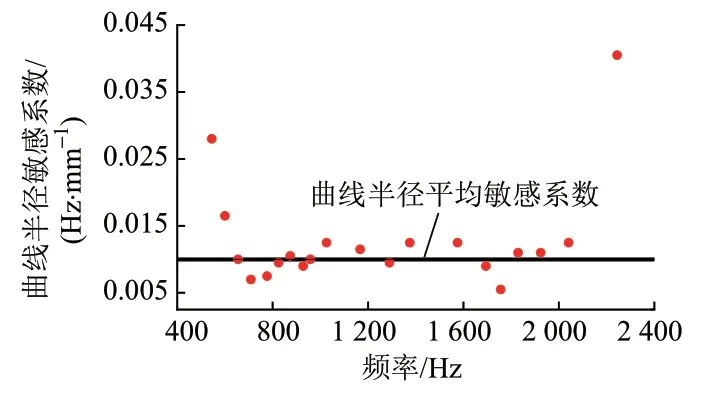
图11 各阶固有频率对曲线半径的敏感性
2.3 扣件间距对振动特性影响分析
对不同扣件间距的曲线线路进行谐响应分析。扣件刚度取15 kN/mm,曲线半径取800 m,扣件间距分别取0.56、0.58、0.60、0.62、0.64 m,依次编号为工况10—工况14,取工况12 为标准工况。通过谐响应分析,得到不同扣件间距下的频率加速度曲线。提取各工况的钢轨固有频率fk(k= 10 ~14),与标准工况下的钢轨固有频率f12作差,计算其频率变化值Δfk=f12-fk,并得出频率变化均值。由于扣件间距对固有频率影响较大,致使匹配成功各阶频率为500 ~2 300 Hz,故仅对上述频带进行分析。频率变化值及频率变化均值随频率的变化曲线见图12。
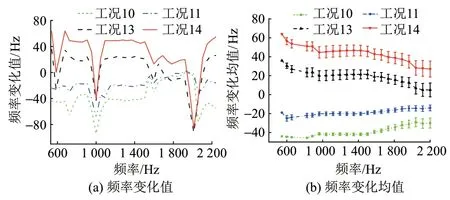
图12 不同扣件间距下各阶频率变化值及变化均值
由图12(a)可知:扣件间距对钢轨各阶固有频率的影响在-90 ~60 Hz;随着扣件间距增加,频率变化值增加。这是因为扣件间距增加,等同于钢轨支撑刚度降低,每阶频率随之降低,与标准工况的差值增大。
由图12(b)可知:扣件间距小于标准扣件间距的工况10、工况11,频率变化均值为负,且随频率增加而呈上升趋势,分别趋近于-30、-14 Hz;扣件间距大于标准扣件间距的工况13、工况14,频率变化均值为正,随频率增加而呈下降趋势,分别趋近于-5、27 Hz。
以5 阶低频和5 阶高频为例,其各阶频率随扣件间距的变化曲线见图13。对各曲线进行拟合,可知频率随扣件间距呈线性变化,线性相关系数均大于0.95。随着扣件间距增加,钢轨支撑刚度降低,每阶频率随之降低。获取每阶频率对扣件间距的敏感性系数,见图14。可知,扣件间距对钢轨频率影响非常明显,敏感性系数约为-1 Hz/mm。
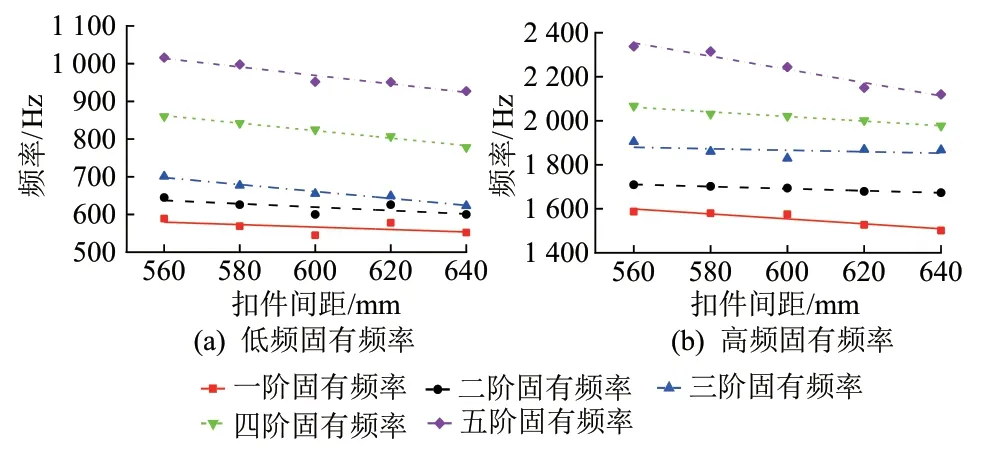
图13 钢轨固有频率随扣件间距变化曲线
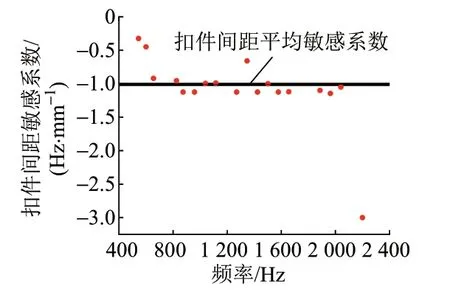
图14 各阶固有频率对扣件间距的敏感性
3 结论
1)扣件刚度对单价固有频率有显著影响的区域主要集中于500 ~ 1 400 Hz 内,变化值在-4 ~ 8 Hz;随着统计阶数增多,多阶频率变化均值趋近于稳定;频率变化均值随扣件刚度增大而增大;单价固有频率随扣件刚度近似线性变化,二者正相关,扣件刚度敏感性系数在0 ~0.5 Hz/(kN/mm)。
2)曲线半径对单价固有频率有显著影响的区域主要集中于500 ~ 1 000 Hz内,变化值在-9 ~ 12 Hz;随着统计阶数的增多,多阶频率变化均值趋近于稳定;频率变化均值随曲线半径增大而增大;单价固有频率随曲线半径近似线性变化,二者正相关,曲线半径敏感性系数约0.01 Hz/mm。
3)扣件间距对单价固有频率有显著影响,变化值在-90 ~60 Hz;随着统计阶数的增多,多阶频率变化的均值趋近于稳定;频率变化均值随扣件间距增大而减少;单价固有频率随曲线半径近似线性变化,二者负相关,扣件间距敏感性系数约-1 Hz/mm。
