基于一题多解 发展科学思维——以第38届物理竞赛预赛第13题为例

吕艳坤 卢 杰 魏 森

（1.东北师范大学教育学部，吉林 长春 130024；2.郑州实验外国语中学，河南 郑州 450052；3.东北师范大学附属中学，吉林 长春 130024）

一题多解是物理教学中常用的教学手段，旨在通过对于方法合理性的判断、对于方法便捷性的对比、对于方法适用性的反思来拓宽解题思路，进而提高学生的科学思维能力.［1］本文以第38届全国中学生物理竞赛预赛第13题为例，探寻指向学生科学思维发展的习题教学策略.

1 原题再现

6个小朋友在操场上玩追逐游戏.开始时，6个小朋友两两间的距离相等，构成一正六边形.然后每个小朋友均以不变的速率v追赶前面的小朋友（即小朋友A追B、B追C、C追D、D追E、E追F、F追A），在此过程中，每个小朋友的运动方向总是指向其前方的小朋友.已知某一时刻t0=0，相邻两个小朋友的距离为l，如图1所示.试问：

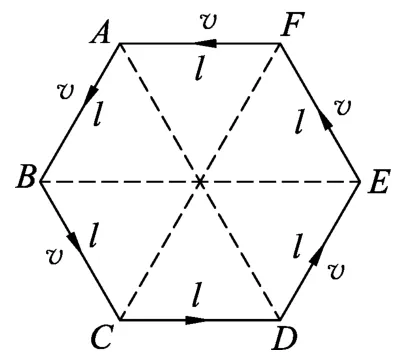
图1

（1）从t0时刻开始，又经过多长时间后面的小朋友可追到前面的小朋友？

（2）从t0时刻开始，直至追上前面的小朋友，每个小朋友又跑了多少路程？

（3）在t0时刻，每个小朋友的加速度大小是多少？

2 试题分析

本题为物理竞赛中典型的曲线追及问题，与之类似的还有猎犬追狐狸（狐狸沿直线，猎犬沿曲线）和猎犬追狼（狼沿圆周，猎犬沿曲线）.其共同点是追及者速度大小不变，速度方向始终指向被追击者且时刻发生在变化，需要从时间和二维空间同时来考虑相遇.

2.1 标准答案解析

由对称性知，每个小朋友运动情况是一样的，以小朋友A为例.

（1）在从小朋友A到小朋友的B连线方向上，小朋友A相对于B的速度分量为

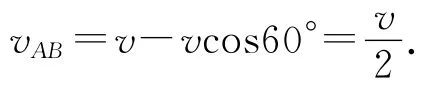
小朋友A追上B的时间为

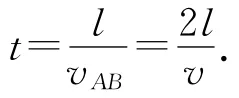
（2）从t0时刻开始，直至追上前面的小朋友，每个小朋友所跑的路程为

s=vt=2l.

如图2所示，设经d t时间小朋友A运动到A′点，小朋友B运动到B′点，小朋友A的速度方向变为从A′点指向B′点，转过的角度为dθ.由余弦定理得

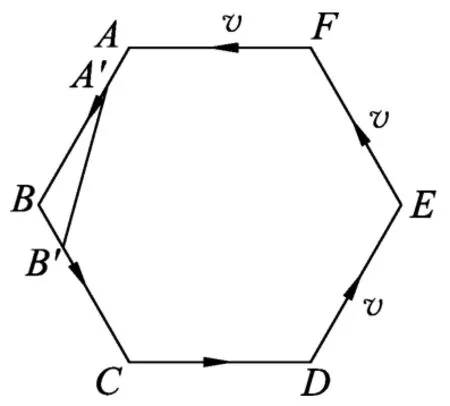
图2

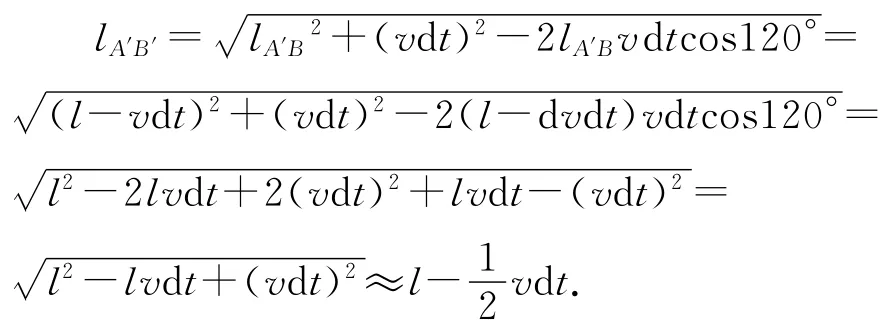
由正弦定理得

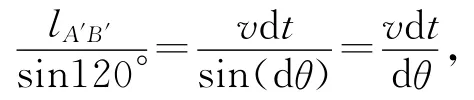
式中dθ为△A′BB′中两边lA′B与lA′B′之间的夹角.

小朋友A运动的角速度为

小朋友A运动的法向加速度为

则小朋友A的加速度大小为

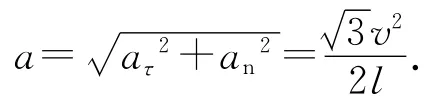
2.2 标准答案评析

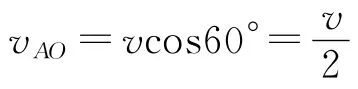
图3

第（2）问，求运动路程.可由s=vt求得，一旦第（1）问追及时间确定，路程也随即求得，因此本文不再赘述.

第（3）问，求加速度大小.标准答案采用的是自然坐标系下分别求小朋友的切向加速度和法向加速度.在法向加速度计算过程中首先采用微元思想构建一个三角形，在三角形中利用余弦定理和正弦定理求得小朋友在初始时刻的角速度，进而得到法向加速度和实际（合）加速度.微元思想是基于宏观事物的普遍性（共性）不仅存在于事物发展的全过程中，而且也包含在微元的特殊性（个性）这一基本属性的基础上，而产生的一种创造性思维方式，往往能起到化曲为直、化难为易、化繁为简的功效.［2］自然坐标系的运用，看似直观，但是实际计算过程较为繁琐，还需要用到正弦定理和余弦定理等数学知识，对学生跨学科能力要求较高.

纵观整个标准答案解析过程，虽然涉及的方法多样，但是存在一定不足：（1）解题方法跳跃较大，缺乏整体的连贯性；（2）方法与方法之间缺乏整合，迁移性有限，易引发学生的思维混乱；（3）总体计算量过大，未体现出物理学科的清晰、简洁之美.

3 多解赏析

为了激发学生学习兴趣，培养学生科学思维，彰显物理逻辑的科学、严谨与连贯，本文采用微积分和极坐标方法，分别从微观和宏观两个角度进行多解赏析.

3.1 微积分方法

设在很短一段时间d t之后，6个小朋友分别到达新的位置，如图4所示，过D′做CD所在线段的垂线D′P，则在△C′D′P 中满足勾股定理

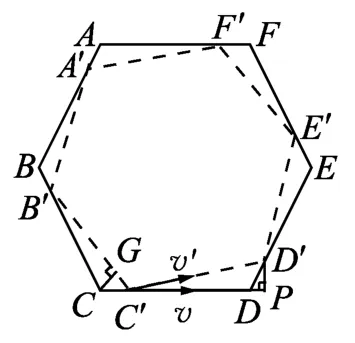
图4

展开后可得

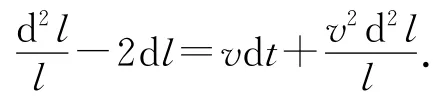
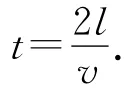
如图4所示，过C点作B′C′边的垂线CG，由于顶角很小，则△B′CG近似为等腰三角形.速度偏转角和位移偏转角相等，速度矢量三角形是一个顶角很小的等腰三角形，则△B′CG和速度矢量三角形相似，易得

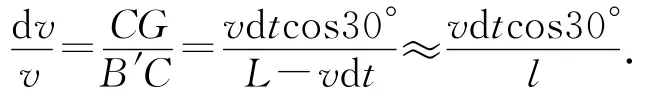
变形可得

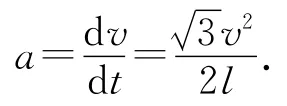
评析：自牛顿和莱布尼兹提出微积分以来，微积分就与物理学的发展密不可分.但是考虑到高中生认知水平和数学基础，高中物理有意避开了使用微积分，物理竞赛对微积分也不作要求.近年来由于竞赛难度的加大，对数学能力要求进一步提高，微积分作为高等数学的基础已成为物理竞赛学习的必备知识.从微积分入手解决竞赛问题，有助于学生从微观层面认识事物变化的本质，从时间与空间融合的双重视角分析事物变化的规律.

3.2 极坐标方法

如图5所示，以中心O为原点建立平面极坐标系，以小朋友E为研究对象，由题意得

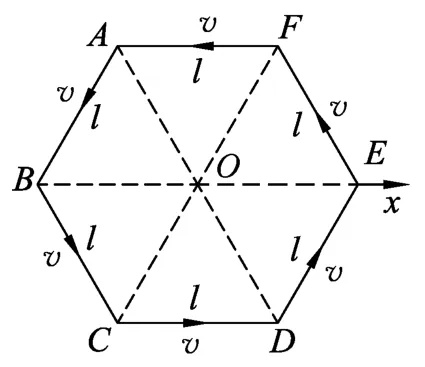
图5

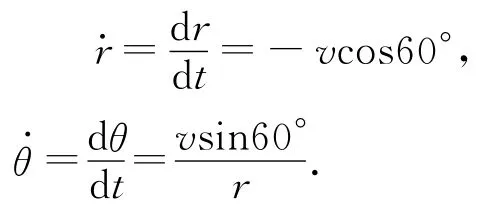
对时间积分可得极径r关于时间的表达式为

根据极坐标加速度公式

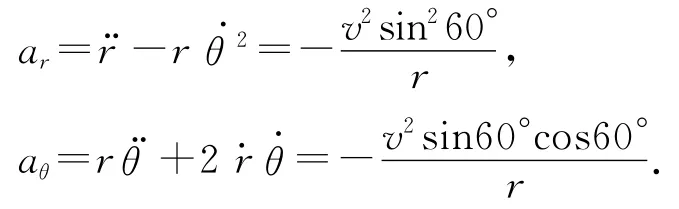
初始时刻，r=l，由a=arer+aθeθ且er⊥eθ可得

评析：笛卡尔坐标系、自然坐标系和平面极坐标系是解决平面物理问题最常见的3种坐标系.对于此类型追击非常规的直线或圆锥曲线运动问题，笛卡尔坐标系会使计算过程变得极为繁琐，不宜采用；自然坐标系在标准答案里已有使用，故不再赘述.平面极坐标系虽然是复赛和决赛考试内容，但是在涉及平面曲线运动过程（尤其是有心运动）时，选取平面内一点为参照原点，在规定极轴后以极径和极角来描述物体的空间位置，将复杂的物理运动过程转化为简洁的数学公式，在对物体进行运动分析时极为方便.［3］3种坐标系的对比分析，有助于学生深化对于坐标系的适用范围和优劣势的理解，对于其后续学习提供基础性支撑.