关于单棒切割磁感线情境中安培力冲量的探讨
2022-07-11王晓辉
王晓辉
(山东省泰安市教育科学研究院,山东 泰安 271000)
冲量是力在时间上的积累,高中阶段恒力或随时间线性变化力的冲量均可直接定量求解,而随时间非线性变化力的冲量往往通过动量定理等方法间接求解.有一种特殊力,即单棒切割磁感线问题中的安培力,它随时间按指数函数非线性变化,但它的冲量却随空间位移均匀变化,由此编制的定量求解题目成为考查学生能力的一类好题,在高考试卷中也身影不断.下面就来探讨这个特殊的冲量和因此造就的特殊运动形式.
1 问题提出
如图1所示,水平放置的光滑U形金属导轨间距L,左端接一个阻值为R的电阻.空间存在竖直向上的匀强磁场,磁感强度大小为B.一质量为m、电阻为r的导体棒,垂直导轨置于导轨平面上,与导轨接触良好,导轨电阻忽略不计,现给导体棒一个水平向右的初速度v0,设t=0时,x=0,v=v0.试讨论:
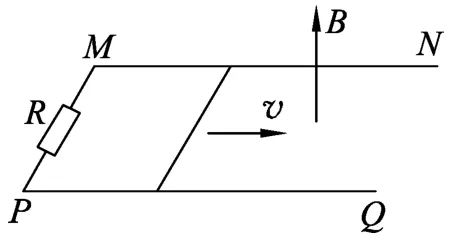
图1 讨论模型
(1)安培力冲量与滑行位移x的关系;
(2)导体棒滑行的速度和滑行的位移x的关系;
(3)导体棒所受安培力与速度的关系;
(4)导体棒所受安培力与位移的关系;
(5)通过导体棒的电荷量与位移的关系.
讨论:由动量定理有

(1)安培力冲量为
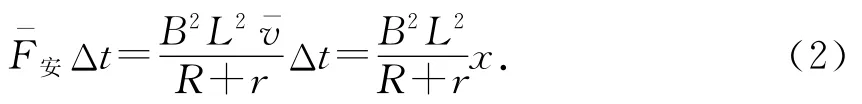
安培力的冲量与滑行位移x呈线性关系.
(2)由(1)、(2)式得

速度与位移呈线性关系,这也是我们常说的“另类匀变速直线运动”关系.
(3)所受的安培力为

棒受安培力与运动速度呈线性关系.
(4)由(3)、(5)式得

棒受安培力与运动位移呈线性关系.
(5)电荷量为

棒中通过的电荷量与棒的运动位移呈线性关系.
我们以安培力冲量与位移成正比以及安培力作用下速度与位移的“另类匀变速直线运动”[2]为核心展开下面题目的探讨.
2 安培力作用下导体棒的运动
2.1 经典模型
例1.如图2所示,已知导体棒的质量为m=5 g,光滑U形导轨水平固定且足够长,其宽为L=0.4 m,左端接有电阻R=1Ω,导轨电阻不计,匀强磁场磁感应强度B=0.5 T.若棒保持与导轨垂直且接触良好,以某一初速度沿平行导轨方向开始运动,经一段时间后停止.测得棒从运动到停止的过程中通过导线的电荷量q=10-2C,棒接入电路部分电阻r=1Ω.试求棒运动的位移x与初速度v0的大小.

图2 安培力阻尼
解析:由(7)式可知
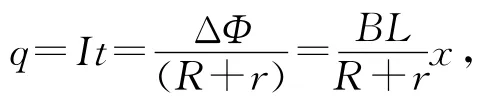
得x=0.1 m.
2.2 分段变式
例2.如图3所示,空间等间距分布着水平方向的条形匀强磁场,竖直方向磁场区域足够长,磁感应强度B=1 T,每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5 m,现有一边长L=0.2 m、质量为m=0.1 kg、电阻R=0.1Ω的正方形线框MNOP以v0=7 m/s的初速从左侧磁场边缘水平进入磁场.求:线框能穿过的完整条形磁场区域的个数n.

图3

2.3 驱动变式
例3.如图4所示,两条相距L的平行金属导轨位于同一水平面内,其左端接一阻值为R的电阻,质量为m的金属杆静置在导轨上,其左侧的矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下.当该磁场区域以速度v0匀速地向右扫过金属杆后,金属杆的速度变为v.金属杆ab的电阻为r,导轨的电阻不计,导轨光滑且足够长,杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:
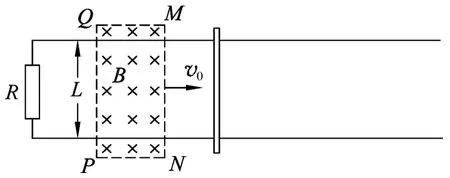
图4
(1)若磁场部分区域扫过金属杆经历的时间为t,那么杆加速运动的距离s是多少?
(2)要使杆获得最大速度,磁场宽度PN应满足的条件是什么?

(2)导体棒最大速度为v0,由(8)式得
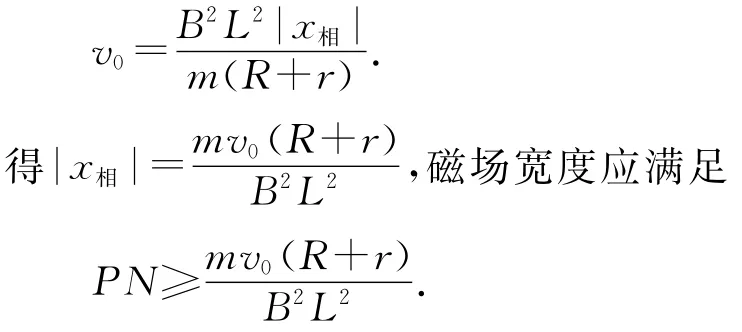
3 恒力牵引背景下导体棒的运动
3.1 经典模型
例4.如图5所示,水平地面上固定一U形光滑导轨,导轨间距为L,导轨电阻均不计,左端接有一阻值为R的定值电阻,质量为m的导体棒垂直导轨放置,整个装置置于磁感应强度为B,方向竖直向下的匀强磁场中.导体棒接入电路部分电阻为r.现给导体棒一水平向右大小为F恒力作用,让其由静止开始运动,已知导体棒运动到稳定速度所用的时间为t,求在此过程中导体棒运动的位移x.

图5

由此看出此运动可以分解为两个分运动:一个是恒力F作用下的匀加速直线运动,即(9)式中的第1项;一个是安培力作用下的“另类匀减速直线运动”,即(9)式中的第2项.由以上各式得
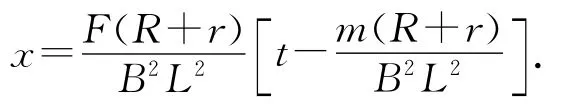
3.2 多过程变式
例5.已知金属棒的质量为m,接入电路部分电阻为r,光滑水平导轨固定且足够长,其宽为L,左端接有电阻R,导轨电阻不计,匀强磁场磁感应强度为B.如图6所示,若棒在水平向左的恒力F作用下,以初速度v0从x=0处沿导轨水平向右运动,运动过程中棒始终与导轨紧密接触且保持垂直,经时间t后又返回x=0处.

图6 往复双程
(1)分析比较导体棒向右运动时间和向左运动时间的长短;
(3)求棒返回x=0处时的速度大小v.
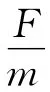


图7
(3)向右过程:
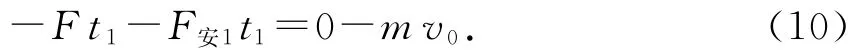
向左过程:

设向右最大位移为xm,则

由(10)、(11)式有F(t1+t2)=mv+mv0,得

4 结语
通过安培力冲量的空间线性特性在不同情境中的应用探讨,形成对其立体、丰富的认知,从而在更为复杂的情境中快速、准确地进行模型识别,实现复杂问题的简单化和程序化.我们还可将探讨融入常见重力、摩擦力、弹簧弹力、与速度或与位移呈线性关系的各种力,做进一步的研究和总结.
