基于变正则化参数仿射投影算法的PMSM参数辨识

汪世平，祝海荣，蔡 慧，邹志杨，马玉龙

(1.南瑞集团有限公司(国网电力科学研究院有限公司)，南京 211106；2.国电南瑞科技股份有限公司，南京 211106；3.中国计量大学 机电工程学院，杭州 310018)

0 引 言

永磁同步电机(以下简称PMSM)凭借其较高的转矩密度和优越的控制性能，在工业要求日趋严苛的环境下，占领的市场份额逐渐扩大。电机控制系统的设计一般都基于电机的机器参数，但PMSM是一个非线性、强耦合、多变量的复杂系统，其参数会随工作环境和工作状态时刻变化[1-2]。不管是精确的电机控制器的设计，还是实时控制算法的设计，都离不开准确的电机参数。如果搭建的电机模型不准确，势必会降低控制器的效率和动态性能，影响电机控制算法的稳定运行。这使得电机参数在线辨识逐渐成为一个研究热点。

目前，电机参数辨识主要有两大类：离线辨识和在线辨识。离线辨识具有局限性，其辨识的电机参数是在特定条件下得到的，不具备实时性。参数在线辨识更能实时地体现电机动态特性，提高电机实时控制算法的有效性和可靠性。参数在线辨识的方法主要包括递推最小二乘法、模型参考自适应法、扩展卡尔曼滤波法和各类智能算法等。递推最小二乘法具有较好的鲁棒性，但是会随着数据量的增多趋于饱和，影响辨识的灵敏性和可靠性[3-5]；模型参考自适应法能通过系统的动态响应来调整自适应率，但在模型参考自适应辨识算法中，自适应机构设计较为复杂，不同工作点下PI增益同步困难[6-7]；扩展卡尔曼滤波法能为非线性系统提供较好的递推估计器，通过最小误差方差估计系统的状态变量，但是它的准确性依赖于系统模型，若系统的模型不准确，则最终得到的结果也会存在偏差；神经网络算法虽然具有较好的鲁棒性，但是计算量较大，计算复杂，会占用较多CPU资源，实际应用中也较少采取此类智能算法[8]。

仿射投影算法(以下简称APA)是一种较有吸引力的回波消除算法。但是在APA中需要矩阵求逆，这个矩阵需要正则化，即在其主对角线的元素上加一个正常数。这个正则化参数非常重要，如果选择不当，APA可能永远不会收敛，特别是在低信噪比条件下[9-11]。针对现有文献中辨识算法计算量大的问题，为了减少辨识过程中的计算量，并保证参数的收敛性，本文采用APA对电机参数进行辨识，并提出了一种变正则化参数的APA，以提高参数辨识的准确性和收敛速度。

1 PMSM参数辨识

1.1 PMSM数学模型

为了方便分析研究，将三相静止坐标系下的数学模型变换到d，q坐标系下，其电流的状态空间表达式如下：

(1)

将其转换为离散状态下的时间模型：

(2)

式中：ud,uq为d，q轴下定子电压；id,iq为d，q轴下定子电流；Rs为定子电阻；Ld,Lq为d，q轴下电感分量，表贴式PMSM中，Ld=Lq=L；ω为电机电角速度;ψf为永磁体磁链；Ts为采样时间。

1.2 变正则化参数仿射投影辨识方法

传统仿射投影算法表达式：

(3)

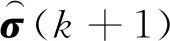
为了提高算法辨识的收敛速度和稳态误差，本文采用了变正则化参数APA。通过随机梯度下降法，寻找参数辨识过程中的正则化参数的最优解，使参数辨识过程能够较为快速且准确，提升辨识算法性能。结合APA的权值更新公式，可以定义代价函数如下：

(4)

式中：e(n+1)为当前的期望输出与辨识算法实际输出之间的偏差；n+1为当前时刻。

正则化参数η的更新方程：

(5)

对代价函数J(n+1)求梯度可得：

μkek(n+1)xk(n+1)xT(n)·

Δk(n+1)e(n)

(6)

式中：

Δk(n+1)=[η(n)+xT(n)x(n)]-1·

(7)

为了消除数据处理过程中不同量纲之间的影响，加快梯度下降求解最优解的速度，对代价函数的梯度进行归一化处理，表达式如下：

(8)

式中：N可以看作是一个符号函数。

为了保证变正则化参数APA的稳定性，一方面需要对梯度算法的学习率参数进行合理的选择；另一方面，由于辨识算法在初始收敛后，可能导致正则化参数向负值跳跃或不断增大，因此，需要设定正则化参数的最小允许值和最大允许值。

假设当正则化参数的值小于输入信号的10 000倍时，认为正则化参数继续减小对参数辨识的收敛速度和稳态误差基本无影响；同理，当正则化参数的值过大时，会严重影响参数辨识的收敛速度，导致参数收敛速度很慢，正则化参数的上限可根据实际情况设定，正则化参数的最小值可定义为如下形式：

(9)

式中：I2为2×2阶单位矩阵。正则化参数的最终表达式如下：

(10)

其中，学习率参数可根据实际的运行状况选择，一般选择较小的参数。为了能够加快收敛，本文采用变学习率参数法。当误差较大时，学习率参数相应放大；当误差较小时，则缩小学习率参数。为了防止收敛过慢，学习率参数Z的最小倍数设定为1，放大倍数根据期望输出与辨识结果的比值确定，表达式：

(11)

式中：odesire为期望输出值；oetimate为辨识结果；ξ为正则因子。该学习率在算法开始时会设定一个初始参数，通过反推法得出正则因子。最终正则化参数的更新表达式：

ηk(n+1)=ηk(n)-Zαsign(N)

(12)

(13)

(14)

(15)

(16)

(17)

由于辨识方程存在欠秩问题[12]，本文的参数辨识主要分为两步进行，即快采样的参数辨识和慢采样的参数辨识，辨识流程如图1所示。具体步骤如下：

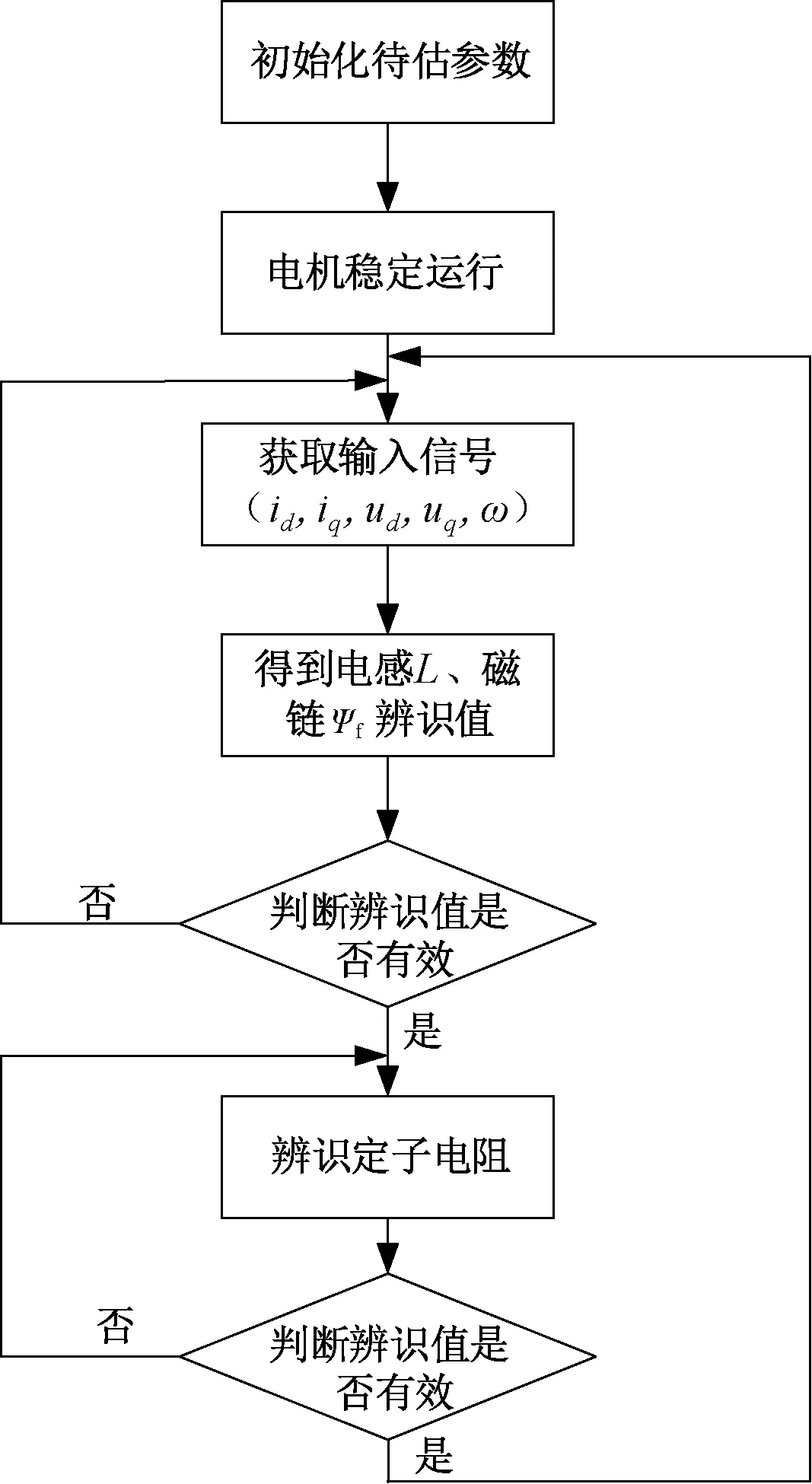
图1 参数辨识流程图

① 当PMSM进入稳态运行时，设置快采样时间Tfast=Tpwm，在此过程中，认为电阻值R是准确且稳定的，将其代入辨识算法中，计算出电机的交轴电感Lq和永磁磁链ψf。

② 判断第一步中辨识的交轴电感和永磁磁链是否有效，若有效，则当其收敛稳定后，将其代入慢采样参数辨识算法中，计算出定子电阻Rs值，设置慢采样时间Tslow=10Tpwm。

2 仿真研究

本文采用id=0的控制方式实现对表贴式PMSM的矢量控制，其矢量控制框图如图2所示。

图2 id =0矢量控制框图

该矢量控制系统是一个双闭环的控制结构，由速度环和电流环串级结构组成。其中，速度环为外环，其作用是敏锐地跟踪上级系统的速度给定，并减小转速波动，使系统工作在稳定状态。电流环作为内环控制器，其输入信号为电流偏差，输出为参考电压，控制电机的转矩。电流内环能够在电机的起动过程中给予允许的最大起动电流，同时抑制外部扰动，加快系统的动态响应，提高系统稳定性。

图3为在MATLAB/Simulink环境中搭建的仿真模型,电机仿真模型内部参数如表1所示。根据参数辨识流程图和系统框架图，搭建基于APA的参数辨识仿真模型，具体模型如图4所示。

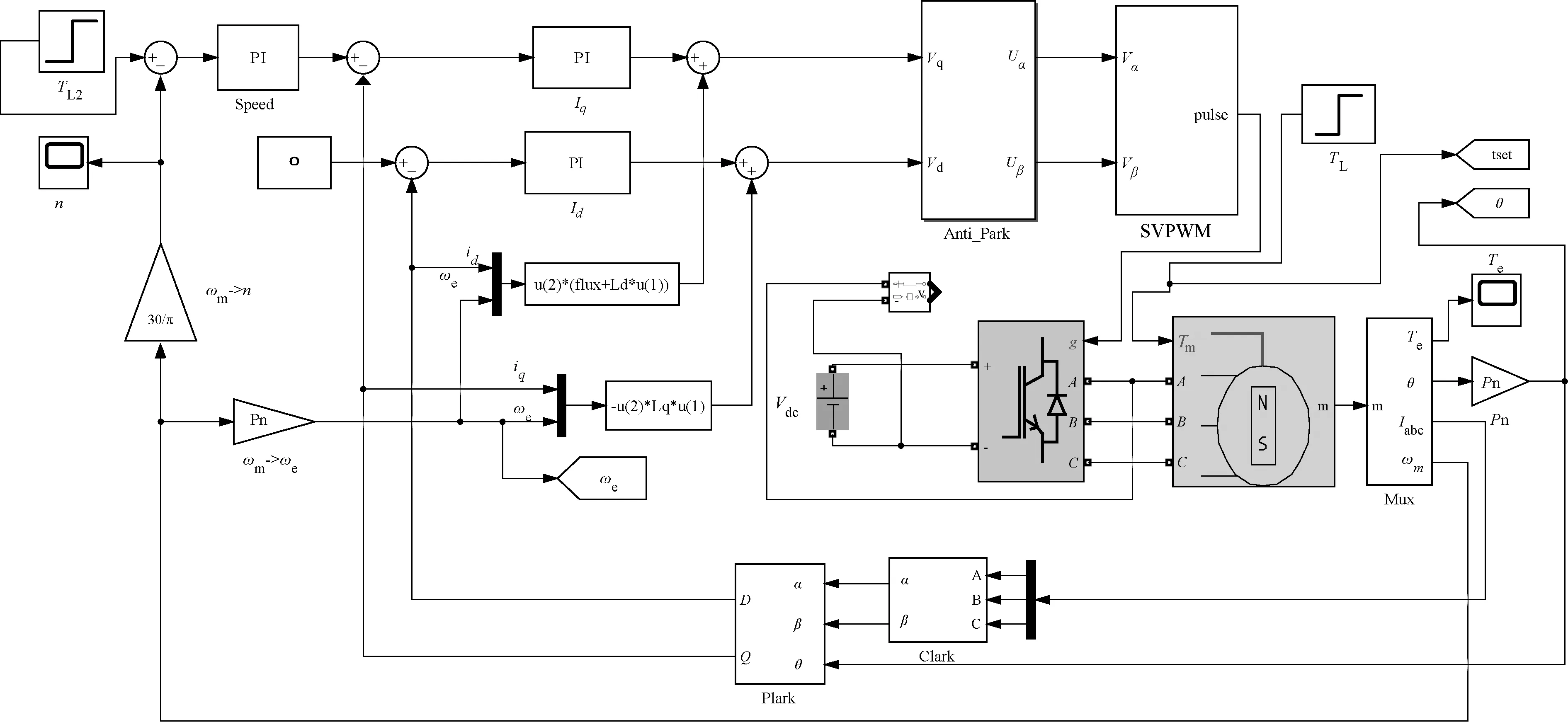
图3 表贴式PMSM矢量控制仿真模型

表1 PMSM内部参数

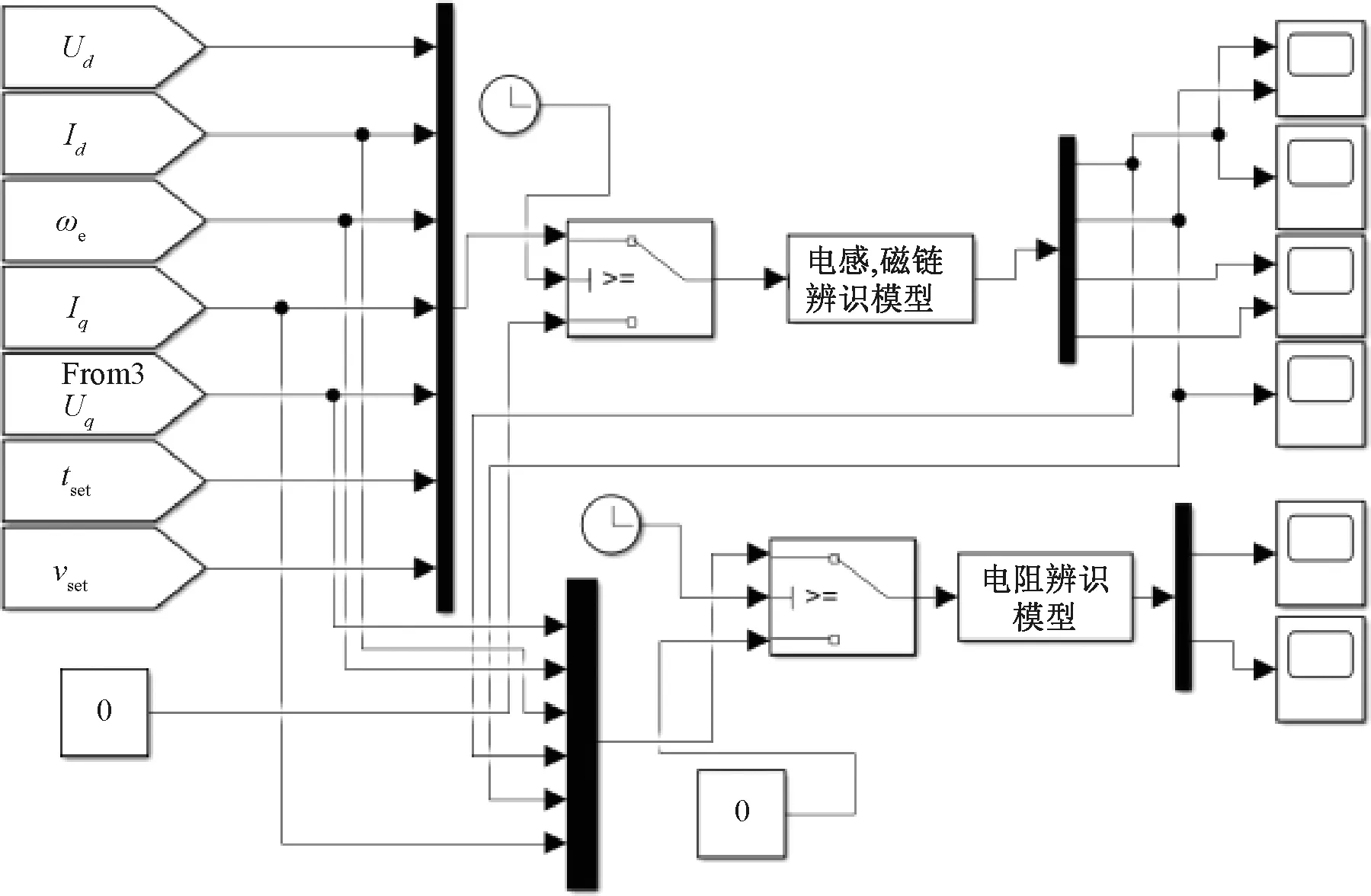
图4 基于APA的参数辨识模型

为了验证本文方法的优点，首先采用传统APA对电机参数进行辨识。设定仿真模型中，电感和磁链辨识算法中的迭代步长μ=[0.1,0;0,0.5]，正则化参数η=[0.1,0;0,0.1]，电阻辨识算法中迭代步长μ=0.1，正则化参数η=0.08。电机在转速800 r/min，负载转矩3 N·m下运行，电感和磁链从0.08 s开始辨识，电阻在电感和磁链辨识结果基本稳定后再进行辨识。辨识结果如图5所示。

图5 传统APA辨识波形

为了验证所提出的参数辨识方法能够在保证收敛速度的同时，降低辨识的稳态误差，取较小的正则化参数值进行对比，设定将电感磁链辨识中的正则化参数η=[0.000 1,0;0,0.000 1]。辨识的稳态波形如图6所示。

图6 传统APA辨识稳态电感磁链波形

图7为基于变正则化参数APA的辨识波形图。仿真条件如下：给定转速为1 000 r/min，t=0时转矩为3 N·m，t=0.3 s时转矩突变至5 N·m，电感磁链辨识算法中，迭代步长μ=[0.1,0;0,0.5]，正则化参数初始值η=[0.1,0;0,0.1]，学习率参数Z=0.01。电阻辨识算法中，μ=0.1，η=0.5，α=0.1。

图7 转矩突变时，基于变正则化参数APA辨识波形

图7中，基于变正则化参数的APA能快速有效地辨识出待估参数，其中电感L的辨识结果为0.011 99 H，辨识误差为0.1%；磁链的辨识结果为0.018 25 Wb，辨识误差为0.1%；电阻R的辨识结果为0.955 Ω，辨识误差为0.3%。图7圈中放大部分的纵坐标尺度与图6相同。对比图7与图5可得，改进的变正则化参数APA收敛速度更快，且收敛后的稳态误差也较小。对比图7和图6可得，改进的参数辨识算法能够有效降低辨识的稳态误差，提高了电感参数的辨识精度。

图7仿真条件下，电感、磁链和电阻辨识算法中的正则化参数变化波形如图8所示。

图8 改进算法中的正则化参数波形

同时，为了验证改进算法在电机转速突变时也能快速地跟踪响应，设置仿真条件为给定初始转速为800 r/min，负载转矩为3 N·m，t=0.3 s时转速突变为1 000 r/min。以电感和磁链为例，仿真波形如图9所示，图9(a)为参数辨识波形，图9(b)为正则化参数变化波形。

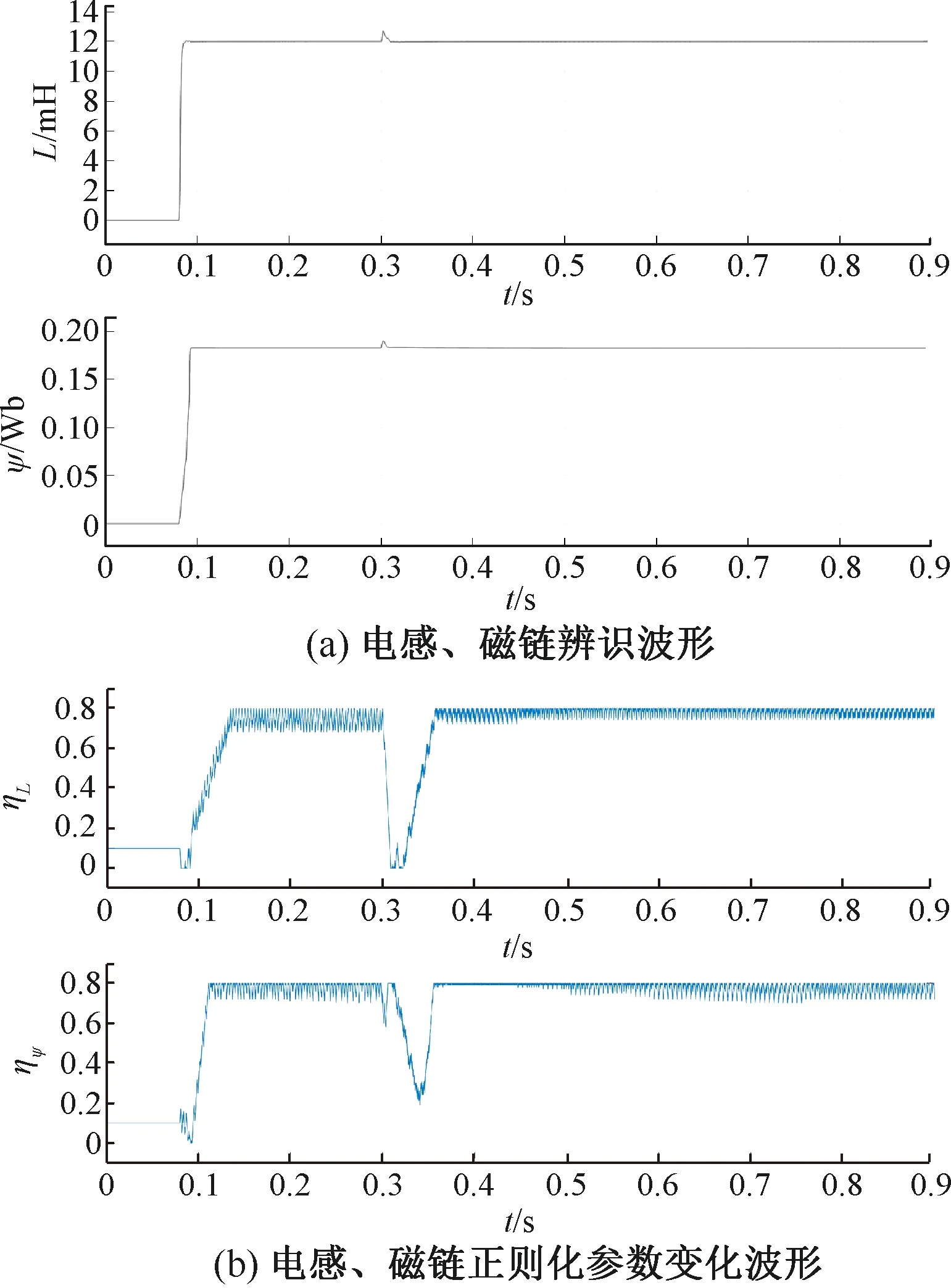
图9 转速突变条件下改进算法的辨识波形

通过图7和图9可以看出，由于本算法的迭代步长可以自适应选取，故基于变正则化参数的APA在转矩、转速突变的情况下，依然能快速有效地辨识出待估参数，有较好的收敛性和可靠性，跟踪性能良好。

3 结 语

实际应用中，PMSM参数辨识算法应当在保证参数收敛性的条件下，尽可能地减少计算量，降低计算复杂度，保证辨识算法拥有较好的鲁棒性。针对此目标，本文采用APA实现电机参数的在线辨识，APA的收敛性逼近递推最小二乘法，计算复杂度低于递推最小二乘法。为了提高辨识算法的收敛速度，提高辨识的精度和鲁棒性，本文采用变正则化参数APA，通过梯度下降法寻求最优的正则化参数。仿真证明，变正则化参数APA能够在保证较快的收敛速度的条件下，降低稳态误差，在转矩和转速突变的条件下，也能较快地跟踪响应，鲁棒性较强。

本文的参数辨识方法，其中学习率参数的自适应还有待改进，今后在本文方法的基础上，仍须进一步完善。