基于RBF神经网络的直驱风力发电系统反推控制

周尔卓，沈艳霞

(江南大学 物联网工程学院， 无锡 214122)

0 引 言

随着科技进步，对能源的需求日渐增大，但大量化石能源的使用对环境造成了破坏。清洁、可再生能源的发展吸引了全世界的目光，中国于2020年9月明确提出“碳达峰、碳中和”战略目标[1]。风能资源丰富、清洁无污染，成为关注的焦点之一[2]，实现风能的最大功率跟踪是有效利用风能的关键。然而风力发电系统高阶、强耦合、高度非线性的特点给其控制器的设计带来很大的挑战。

近年来，国内外学者对风力发电系统发电机侧控制方法的研究已取得了一定的成果[3-4]。其中，反推控制在设计此类不确定性系统控制器时因具有全局稳定性和鲁棒性，显示了独特优势[5]。反推控制的基本思想是将原本较为复杂的非线性系统分解成为低于系统阶次的子系统，并对每个子系统设计合适的李雅普诺夫函数和中间虚拟控制量，直至“后退”到整个系统，从而完成整个控制律的设计[6]。

文献[7]中设计了针对永磁同步电机的反推控制器，但控制器设计建立在系统运行时参数没有明显变化的基础上，没有考虑参数变化对系统性能的影响。文献[8]考虑了未知部分扰动设计基于线性参数可变观测器的反推控制器，但由于线性参数可变观测器是一种线性观测器，需要整定的参数较多且无法从理论上保证系统收敛。文献[9]设计了一种滑模自适应控制器，提高了转速追踪性能和抗干扰能力，但采用了传统的sign符号函数，没有对抖振问题进行有效抑制。

为高效利用风能，本文提出基于径向基函数(以下简称RBF)神经网络的反推控制来实现永磁直驱风力发电系统的最大功率控制。利用反推控制设计永磁直驱风力系统控制器，并借助RBF神经网络的学习和逼近能力对系统未知扰动部分进行观测，解决反推控制系统要求模型信息已知的问题，提高风能利用效率和系统稳定性。

1 永磁直驱风力发电系统模型

1.1 风力机模型

风力发电系统将风力机捕获的风能转化为机械能，从而驱动发电机产生电能。风力机产生的机械功率和气动转矩可以由下式表示：

(1)

(2)

式中：P是风力机机械功率；Tm是风力机气动转矩；ρ是空气密度；S是叶片面积；V是风速；ωr是风轮转速；CP(λ,β)是风能利用系数。CP(λ,β)可利用最小二乘曲线拟合方法表示[10]：

(3)

式中：β为桨距角；λ为叶尖速比。

λ和β关系如下：

(4)

叶尖速比定义如下：

(5)

式中：R是风轮叶片半径。

由式(3)和式(4)可以得到风能利用系数-叶尖速比特性曲线，如图1所示。

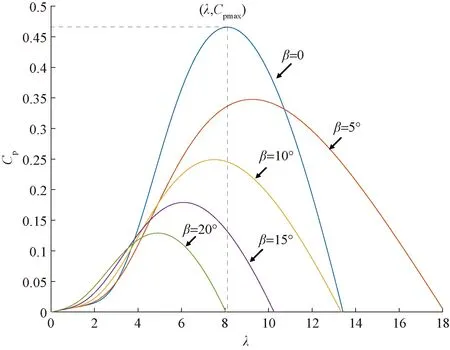
图1 风能利用系数-叶尖速比曲线

由图1可知，当桨距角β变大时，风能利用系数曲线整体随之向下移动。为了保证风能利用系数最优，需要将桨距角β控制在0，即βopt=0可以取得最大的风能利用率CP(λ,β)MAX，且CP(λ,β)MAX对应着一个最优叶尖速λopt。由于直驱永磁同步发电系统中发电机的转子转速ωm与风轮转速一致，即ωm=ωr。在桨距角β确定为0°的情况下，使得系统风力机转速跟踪最优叶尖速比下的转速ωopt以实现最大风能利用率，并有：

(6)

1.2 永磁同步发电机模型

在d-q同步旋转坐标下，建立永磁同步电机的数学模型：

(7)

式中：id、iq分别为发电机d轴和q轴电流分量；Rs为定子电阻；L为发电机等效电感；ud和uq为发电机d轴和q轴电压分量；ψf为永磁体的磁链；p为发电机转子极对数；ωm为发电机转子转速。

(8)

1.3 传动轴模型

本文中研究的是直驱式风力发电机，可以将风力发电系统等效成一个单质量块，如图2所示。

图2 传动链单质量模块模型

系统传动链可以表示：

(9)

式中：J表示连接风机和发电机的转动惯量；B为风机的摩擦系数。

对式(9)整理：

(10)

结合式(8)可得：

(11)

2 控制器设计

定义转速误差e1=ωm-ωopt，控制目标为e1→0。考虑系统中存在的未知扰动部分，结合式(11)可以得到：

(12)

式中：F表示系统总的未知扰动部分。

2.1 RBF神经网络观测器设计

采用反推控制使系统的状态输出跟踪期望轨迹，需要精确的模型信息。但由于系统存在未知扰动部分，需要对未知扰动部分进行估计，消除不确定性对系统的影响。

RBF神经网络因良好的学习逼近能力而受到关注，其具有非线性映射功能，理论上来说可以逼近任意非线性函数[11]。RBF神经网络结构简单，实时性较好，其在线学习的能力可以用在控制器设计中有效解决非线性系统控制问题。图3为RBF神经网络结构示意图。

图3 RBF神经网络结构

其隐藏层采用高斯函数，即：

(13)

式中：V为网络的输入；j为网络隐含层第个节点；h=[hj]T为高斯函数的输出；bj,cj分别为高斯函数的标准偏差和神经元中心坐标。输出层的输出为隐藏层各项线性加权组合：

(14)

本文设计的RBF神经网络观测器中，网络的输入为跟踪误差V=[e1e2]，输出层输出用以逼近非线性部分F：

F=F(x)-δ=WTh-δ

(15)

式中：W为理想权重;δ为逼近误差，且在一定条件下足够小。则非线性函数F的理想估计值可以表示：

(16)

且有：

(17)

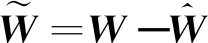
(18)

对于神经网络的标准偏差bj和中心坐标cij,可以用梯度下降法[12]得到:

(19)

cij(k+1)-cij(k)=Δcij(k)+α[cij(k)-cij(k-1)]

(20)

(21)

bj(k+1)-bj(k)=Δbj(k)+α[bj(k)-bj(k-1)]

(22)

2.2 反推控制器设计及分析

构造李雅普诺夫函数：

(23)

对式(23)求导：

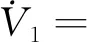
(24)

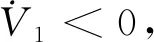
(25)

(26)

η为设置的神经网络学习速率。对上式求导：

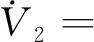
(27)

(28)

(29)

为了实现对d轴和q轴电流的跟踪，定义d轴和q轴电流误差：

(30)

构造如下李雅普诺夫函数：

(31)

对式(31)求导并代入式(7)：

(32)

式中：l1,l2为设计的大于0的常数。为了满足李雅普诺夫稳定性，可以得到d轴和q轴电流环反推控制器设计：

(33)

3 仿真验证

为了验证基于RBF神经网络的反推控制器的性能，基于MATLAB/Simulink进行仿真验证。风力机参数如表1所示，永磁同步发电机参数如表2所示。

表1 风力机参数

RBF神经网络设计中，选取神经网络结构为2-5-1，高斯函数的参数ci选取为[-2， -1， 0， 1， 2],参数bi选取为0.12。自适应参数η选取为120；反推控制器参数k1=50，l1=l2=100。

表2 永磁同步发电机参数

选取如图4的风速曲线验证永磁直驱风力系统在风速变化时系统动态性能。在0～0.2 s内的初始风速为6 m/s，在0.2～0.7 s内风速逐渐爬升至6.5 m/s，在1 s时突变到8 m/s并在2秒时下降到6.5 m/s。

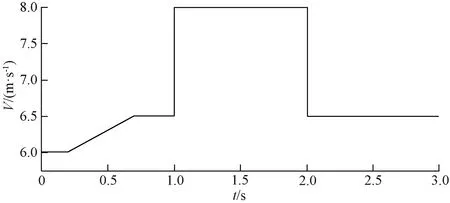
图4 风速曲线

图5为风能利用系数曲线。在风速逐渐爬升和保持不变时，PI控制器和基于RBF神经网络的反推控制器均能使系统风能系数保持在最大风能利用系数0.48。而在1 s和2s风速突变时，PI控制器下系统风能利用系数波动较大，分别跌落6.5%和95%。相比PI控制器，基于RBF神经网络的反推控制器下系统风能利用系数波动较小，在1 s和2 s时，分别跌落6%和16.7%。并且相比PI控制器，基于RBF神经网络的的反推控制器恢复稳定的时间更短。

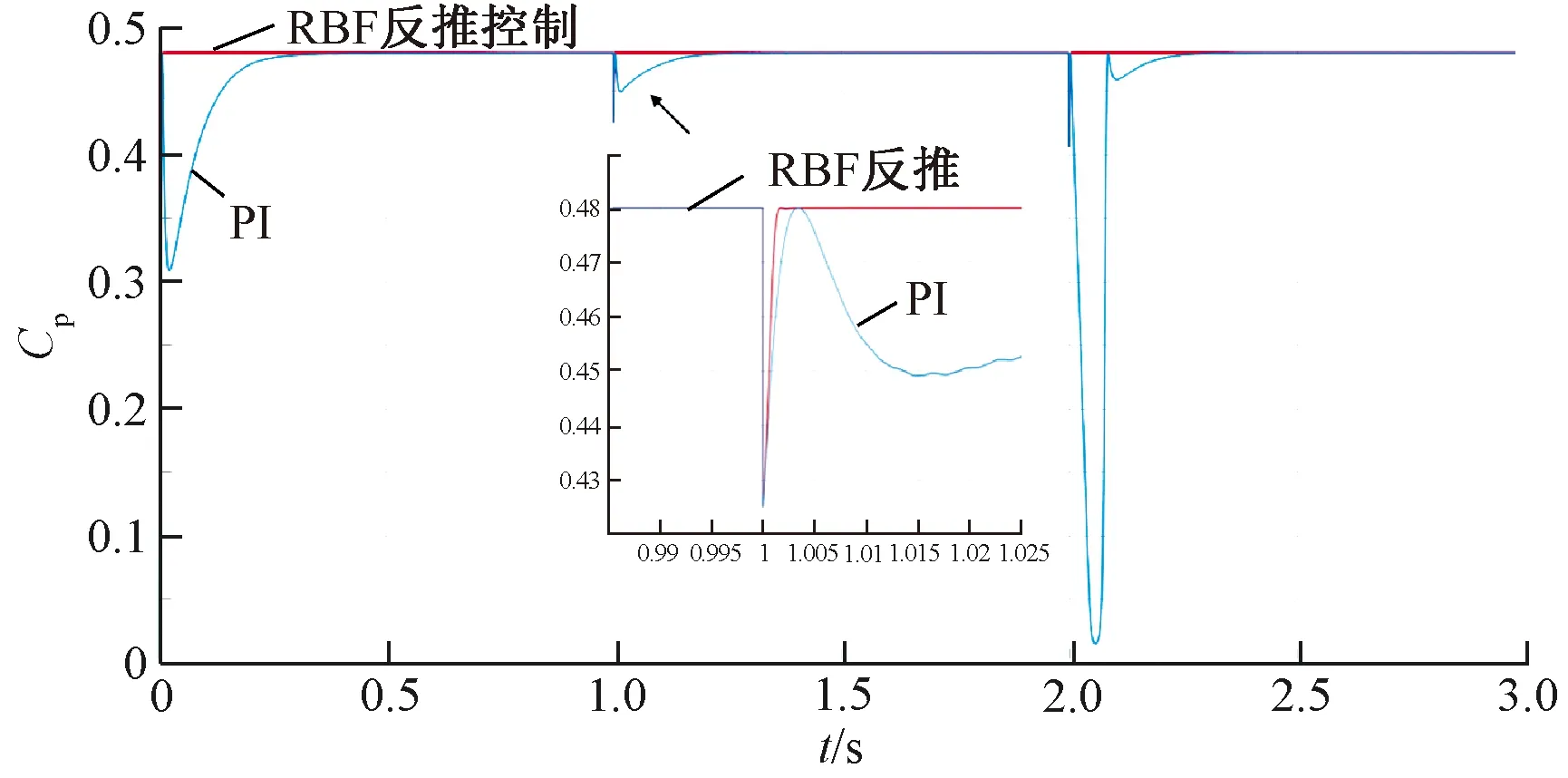
图5 风能利用系数曲线

图6和图7分别为风轮转速曲线和叶尖速比曲线图。在风速逐渐爬升和保持不变时，PI控制器和基于RBF神经网络的反推控制器均能跟踪系统风轮转速理想转速，叶尖速比保持在最优叶尖速比8.1。而当1 s和2 s风速突变时，PI控制器下系统风轮转速和叶尖速比超调较大，且需要0.4 s左右的恢复时间，而基于RBF神经网络的反推控制器下系统的恢复时间只有0.05 s。

图6 风轮转速曲线

图7 叶尖速比曲线

综合图5～图7可以看出，相比传统PI控制器，本文设计的基于RBF神经网络的反推控制器提高了系统的抗干扰能力，能够更好地实现对最大风能的跟踪。

4 结 语

本文对永磁直驱风力发电系统额定风速以下发电机侧控制方法进行了研究。针对永磁直驱风力发电系统的强耦合、高度非线性的特点，利用反推法设计转速环和电流环控制器。通过基于RBF神经网络观测器对系统不确定部分进行观测，解决反推控制需要模型信息已知的问题。仿真结果表明，与传统PI控制器相比，该方法在风速的快速变化时能有效跟踪理想风速，实现对风能最大功率跟踪，提高了风能的利用率。