基于圆感应同步器的低速永磁同步力矩电机控制系统
2022-07-11王林波安群涛
周 力,王林波,王 顺,李 帅,安群涛
(1.中国航发贵州红林航空动力控制科技有限公司,贵阳 550009;2.空军装备部驻贵阳地区第二军事代表室,贵阳 550000;3.哈尔滨工业大学 电气工程与自动化学院,哈尔滨 150001)
0 引 言
低速永磁同步力矩电机(以下简称PMSTM)具有控制性能优异、功率密度大等优点,被广泛应用于直驱系统中[1-4]。为准确获取电机的位置和速度信息,基于光电原理的高分辨率增量或绝对式编码器、正余弦编码器被广泛采用,然而编码器存在环境适应性差的问题[5]。
旋转变压器和感应同步器是基于电磁感应原理的角位移传感器,具有可靠、防辐射能力强等优点,可在恶劣环境场合工作,广泛应用在航空航天等伺服控制系统中[6]。旋转变压器因直径限制,其极对数较少,精度远不及光电式编码器。圆感应同步器与旋转变压器原理相同,不同的是它采用印刷电路工艺,可以大幅增加极对数,从而提高角度测量精度。由于输出绕组匝数少,圆感应同步器的输出电压信号为毫伏级,较低的模拟电压信号容易受到干扰,因此对模拟信号处理电路有较高的要求[7-8]。圆感应同步器可以采用集成旋转变压器数字转换器(RDC)芯片实现角度解调,但RDC位数有限且转速跟踪范围大,导致转速分辨率较低[9-10]。为提高角度和速度解调精度,可采用FPGA进行软件算法解调[11-12]。
本文基于DSP和FPGA设计了采用圆感应同步器作为测角元件的低速PMSTM控制系统,DSP用于完成电机转速和电流双闭环控制,FPGA用于实现圆感应同步器的解调。在圆感应同步器接口电路、输出信号处理电路,采用两级放大来提高信号带宽,经高速ADC采样后在FPGA中进行FIR滤波,再由坐标旋转数字计算反正切算法计算角度,该方案具有算法简单、带宽不受限制的优点,且可以实现较高的解调精度。测试结果验证了本文方案的有效性。
1 永磁同步电机矢量控制
不计高频谐波和非线性,表贴式永磁同步电机在dq坐标系下的数学模型:
(1)
(2)
当忽略摩擦系数B的影响时,电机的机械运动方程:
(3)
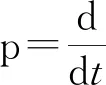
对于表贴式永磁同步电机,采用id=0矢量控制可实现最大转矩电流比运行,系统框图如图1所示。
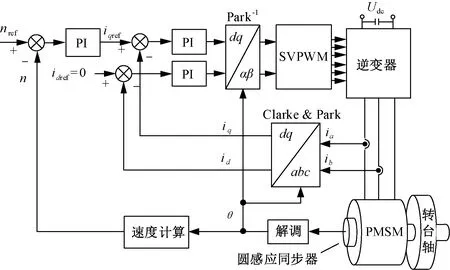
图1 PMSM矢量控制系统框图
2 圆感应同步器的解调
2.1 圆感应同步器
圆感应同步器与旋转变压器原理一样,也是利用交变磁场和互感原理工作的。所不同的是,圆感应同步器的转子和定子绕组均采用印刷电路板,且转子和定子绕组分布是不相同的。圆感应同步器在转子上是连续绕组,导体数目就是圆感应同步器的极数,两相邻导体中心线之间的夹角称为极距;而定子上则是分段绕组,又称为正余弦绕组。正、余弦绕组交错排列,两相之间的距离为(P+1/2)个极距(P为整数),在360°内呈现一个正弦信号及一个余弦信号,构成绝对坐标。
如图2所示,圆感应同步器通常在转子上放置激磁绕组,当通入正弦激磁电压uE=UEsin(ωEt)时,定子两相绕组感生出的电动势如下:
(4)
式中:uA,uB为定子两相绕组感应电动势;UE为转子激磁电压幅值;ωE为激磁电压的角频率。
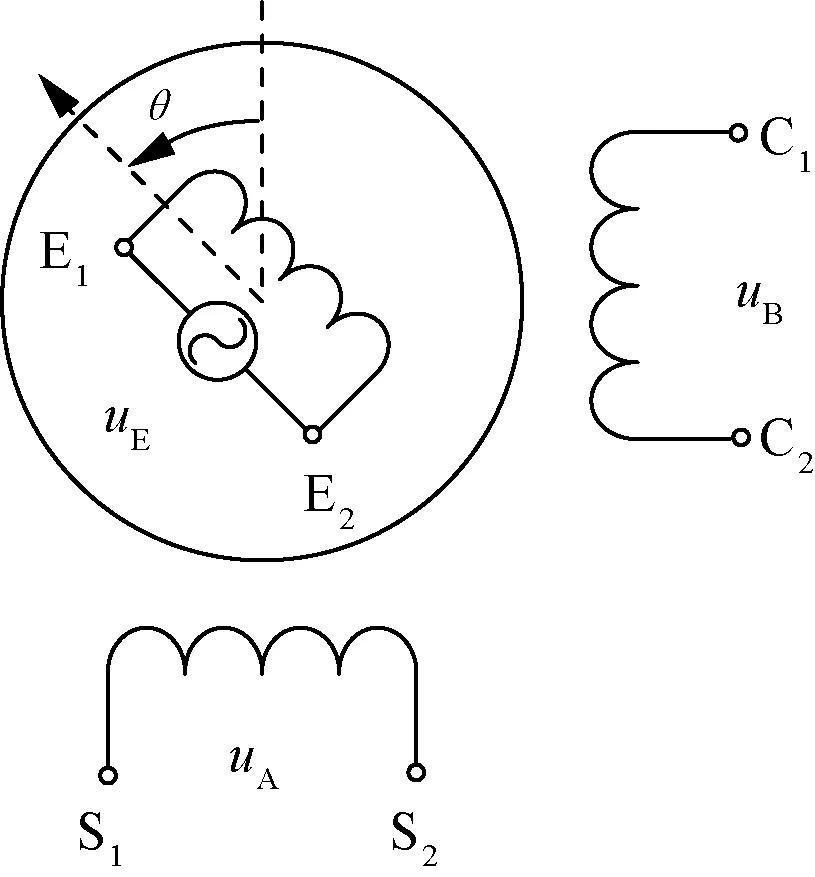
图2 圆感应同步器的绕组关系
2.2 圆感应同步器的解调
采用反正切方式解调圆感应同步器的角度值,整体方案如图3所示。采用高速A/D转换器对圆感应同步器的激磁信号uE和输出信号uA、uB进行过采样,采样频率为激磁频率的2 000倍。采样值送入FPGA经FIR带通滤波器滤除可能存在的直流分量和高频噪声,然后求取反正切得到角度。
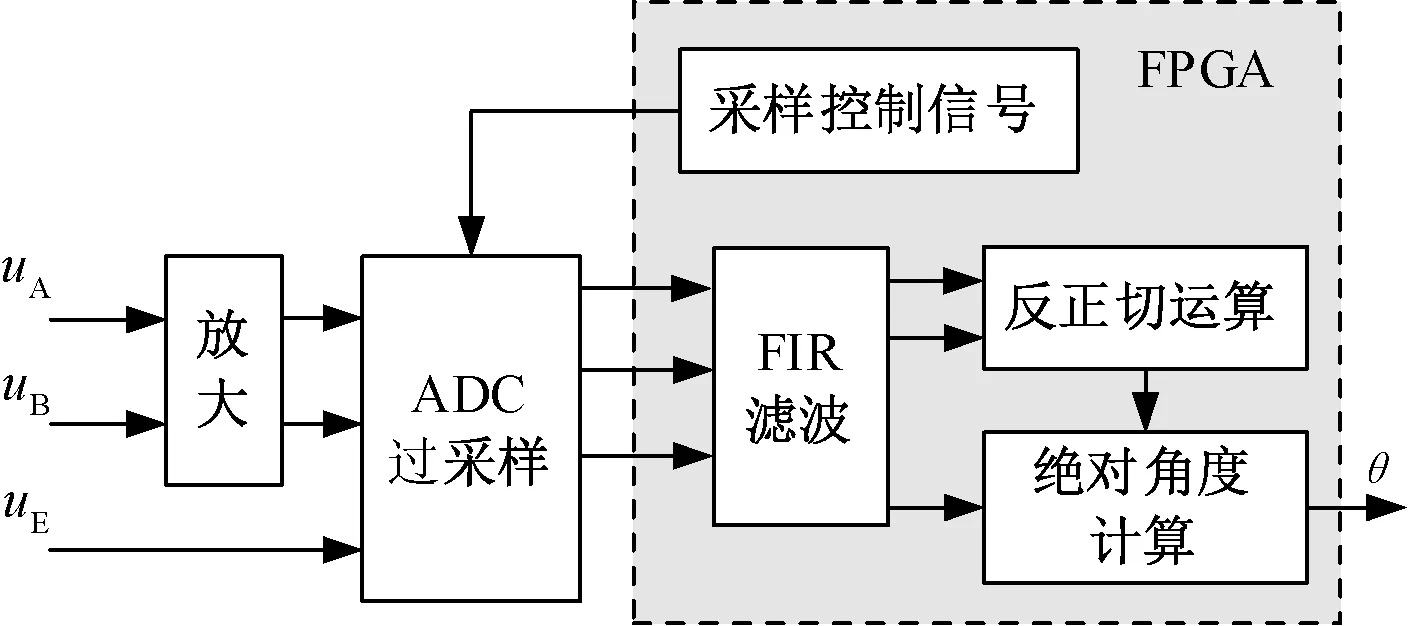
图3 圆感应同步器解调原理框图
反正切求取采用坐标旋转数字计算方法(以下简称CORDIC算法),由Volder J D在1959年提出,基本思想是将复杂函数运算转化为简单的移位和加减运算,把占用资源大的乘法运算转换为加和运算,在计算三角函数、反三角函数、乘法、开方等运算中具有巨大优势。CORDIC算法求反正切的计算原理如图4所示。

图4 CORDIC算法求解反正切的原理图
假设在x,y坐标系中将A点(xA,yA)围绕坐标原点O(0,0)逆时针旋转α角度得到B点(xB,yB),有如下逆时针坐标旋转公式:
(5)
对式(5)提取公因式cosα得:
(6)
以上为A点经一次旋转到达B点的过程,现由任一点的坐标值求取角度值,即求取该点与x轴的夹角θ,同理只需将该点经N次旋转至x轴正半轴上即可。假设第i次旋转的角度为θi,那么由式(6)知,第i次旋转表达式:
(7)
令tanθi=2-i,则第i次旋转角度θi=arctan(2-i)。为使累计旋转角度之和无限接近所求角度,也就是使y无限接近于0,得到CORDIC算法的迭代公式:
(8)
式中:di=±1作为判决因子决定旋转方向,其值取决于前一次迭代后所得yi值的正负。当yi>0时,di=-1,顺时针迭代;反之则di=1,逆时针迭代。
因此,角度累加公式:
(9)
上述角度累加结果即为所求的角度值。CORDIC算法的迭代次数取决于系统需求的精度和信号的采样精度。
3 PMSTM驱动系统设计
3.1 系统的硬件结构
低速PMSTM驱动系统硬件结构如图5所示。逆变器由6只MOSFET分立器件构成,型号为HYG180N10LS1D;主控芯片采用DSP,用于完成矢量控制算法;选用Altera Cyclone IV系列FPGA 中的EP4CE22完成圆感应同步器信号的解调。
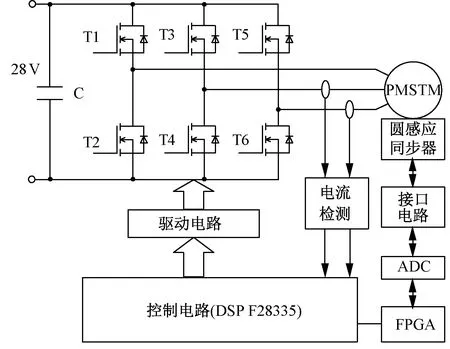
图5 驱动系统硬件结构图
3.2 圆感应同步器信号接口电路设计
本文采用360对极圆感应同步器,其信号接口电路结构如图6所示。由ICL8038产生正弦信号经OPA548放大后作为激磁信号施加到激磁绕组上,激磁信号为10 V(峰峰值) 5 kHz;正余弦绕组输出信号约为4 mV(峰峰值),分别经过由运放AD620和TP2272构成的两级放大电路放大后送入A/D转换器。A/D转换器分别采集激磁信号和正余弦绕组输出信号,将其转换为数字量送入FPGA中进行角度解调运算。
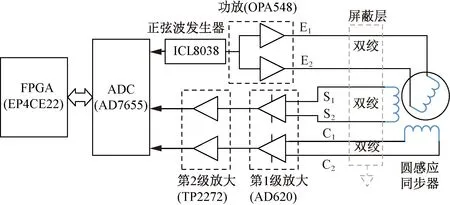
图6 圆感应同步器接口电路
4 实验结果
在设计的低速PMSTM驱动系统样机中对解调算法和系统运行性能进行实验测试。电机参数:额定电压28 V、额定转速30 r/min、额定电流2.4 A、相电阻1.4 Ω、交直轴电感6.2 mH、极对数为15;所用圆感应同步器为360对极,激磁电压有效值为7 V,激磁频率10 kHz;逆变器开关频率为10 kHz。图7给出了圆感应同步器输出经放大后的正余弦包络线信号和解调出的角度。图8为电机低速运行测试结果,图8(a)为斜坡给定的转速响应波形,稳态转速为0.6°/s,电机运行平稳,转速波动在±5%以内;图8(b)为0.006°/s阶跃给定下的响应曲线,经过动态过渡过程后,稳态转速波动在±15%以内。
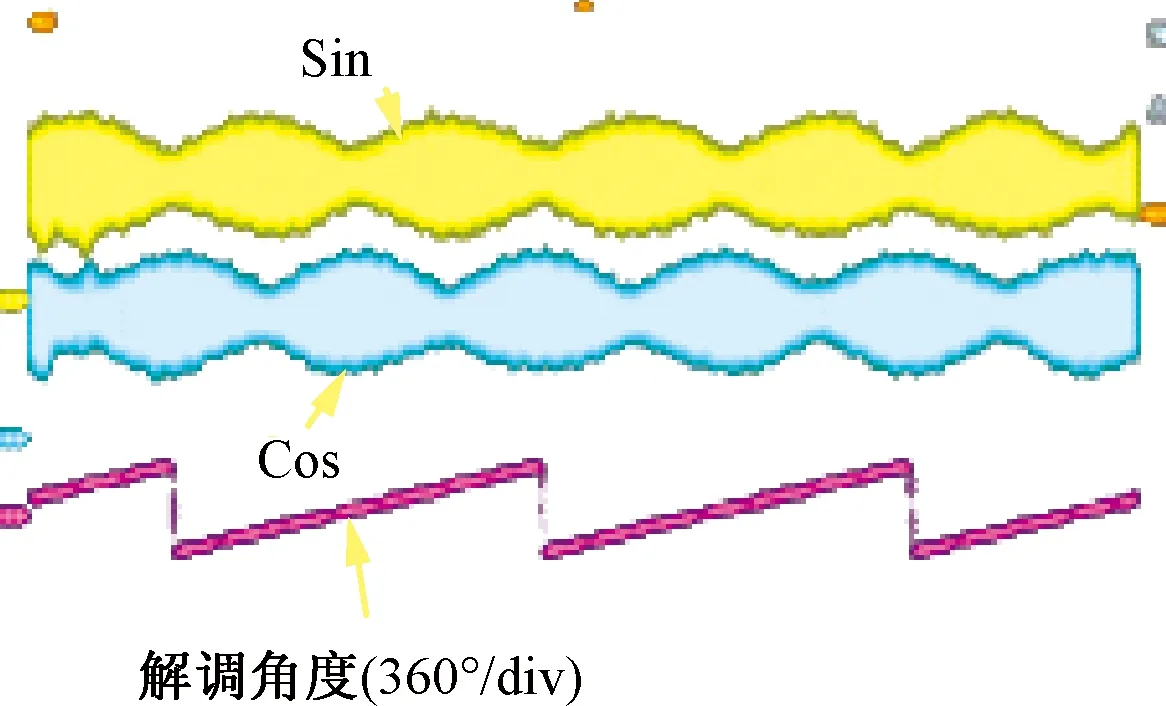
图7 解调测试结果
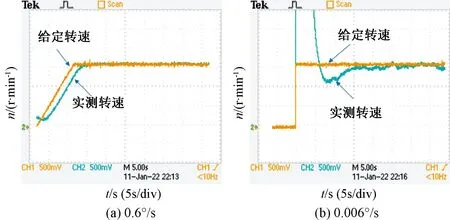
图8 低速运行测试结果
5 结 语
低速PMSTM控制系统中采用圆感应同步器作为测角元件可以获得较高的测量精度,适用于对使用环境要求高的应用场合。本文针对360对极圆感应同步器,设计了接口电路和基于FPGA的解调算法,实现了角度的精密解调。实验测试表明,电机在0.006°/s转速下运行平稳。
