横隔板加劲肋对钢桥面板疲劳细节受力的影响

陈壮壮 吉伯海 姚 悦 袁周致远

(河海大学土木与交通学院 南京 210098)

0 引 言

正交异性钢桥面板凭借其自重轻、承载力强及施工速度快等优点，在大跨度钢结构桥梁中得到了广泛的应用[1-2]．正交异性钢桥面板主要由盖板、纵肋和横隔板组成[3]，在钢箱梁桥的设计中，横隔板上会设置加劲肋以增加横隔板的刚度．由于横向加劲肋与弧形缺口之间的过渡段较短，横隔板在车辆荷载下的变形可能产生变化，会对弧形缺口等构造细节的受力产生影响．

正交异性桥面板的附属构造会对桥面板疲劳细节的应力及变形产生影响．王伟等[4]对正交异性板U肋处设置小隔板和支撑板的构造进行了疲劳试验，研究表明U肋内部设置开孔的小隔板和支撑板可以有效降低弧形缺口、横隔板和U肋焊趾细节的应力．叶枝等[5-6]研究了横隔板间小横肋构造对U肋与横隔板焊缝末端和横隔板弧形缺口两处疲劳细节的疲劳性能的影响，有限元模拟结果表明:小横肋可以有效降低两处细节的应力幅值．Tian[7]通过有限元模拟和疲劳试验相结合研究了正交异性钢箱梁内增设支撑构件的影响，结果表明:增设支撑构件可有效降低易疲劳细节的应力幅值，增加细节的疲劳寿命．Oh 等[8]研究了U肋内隔板构造，结果表明:内隔板可以显著降低疲劳细节的主应力而不会明显增加结构自重，弧形内隔板的应力改善效果比梯形内隔板更加有效．然而，上述研究均将横隔板简化为一个板件，未考虑其单侧设置的加劲肋．王甜等[9]通过实桥测试，监测横隔板两侧，结果显示横隔板两侧应力时程存在差异，即横隔板存在显著的面外变形，设加劲肋一侧的弧形缺口主应力较大，且U肋两侧的弧形缺口面外变形并不一致．因此，在实桥中横隔板单侧加劲肋的设置会导致两侧损伤的差异，需要明确横隔板加劲肋对典型疲劳细节的影响．

文中依托国内某悬索桥建立有限元模型，考虑不同位置的车辆荷载，分析加劲肋构造对横隔板变形的影响，基于细节的最不利荷载位置，对比分析横隔板设加劲肋与不设加劲肋情况下弧形缺口、U肋与横隔板焊缝疲劳细节的的应力和面内外变形，研究加劲肋构造对弧形缺口、U肋与横隔板焊缝细节受力的影响．

1 有限元模型

1.1 几何模型和材料参数

基于ABAQUS建立国内某悬索桥节段模型，记不设加劲肋的为模型Ⅰ，设加劲肋的为模型Ⅱ，见图1．车辆荷载作用引起主梁体系的应力很小，局部应力分析时采用钢桥面板简化模型是合理有效的，所以建立的节段模型仅保留铺装层、顶板、纵肋和横隔板．横桥向包含六道U肋，U肋尺寸为300 mm×280 mm×8 mm，间距600 mm，从左往右依次编号为1#～6#；纵向设有五道横隔板，厚10 mm，间距3 200 mm，依次编号为A～E．模型Ⅱ中横、竖向加劲肋厚度分别为12、10 mm，竖向加劲肋间距1 300 mm．模型整体采用实体建模，单元类型为C3D8R，其中模型Ⅱ的单元数为85 130．铺装层的弹性模量为1 000 MPa，其余部件均为2.06×105MPa，所有部件的材料泊松比均为0.3．边界条件为约束顶板、铺装层四周和U肋两端的三个平动自由度，约束横隔板端部的全部自由度．

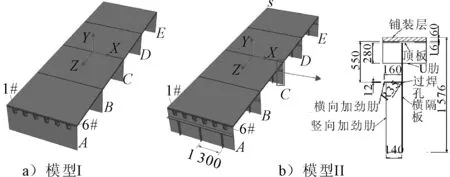
图1 钢桥面板有限元模型(单位：mm)

在全局坐标系原点处建立子模型，尺寸为1 200 mm×400 mm×710 mm，范围为C隔板上方的3#、4#U肋，模型Ⅱ的子模型见图2．

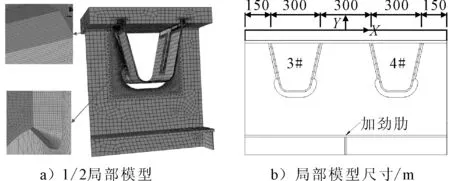
图2 模型Ⅱ子模型

子模型的全局网格尺寸为20 mm，弧形缺口边缘、U肋-横隔板焊缝以及U肋-顶板焊缝全部进行网格细化处理，细化尺寸为1 mm．模型整体采用C3D8R单元，过渡区域用二次四面体单元，子模型共包含430 001个C3D8R单元和299 903个二次四面体单元．子模型边界上导入总模型计算结果中对应节点的全部自由度位移值．

1.2 荷载工况

轮载在纵桥向和横桥向的应力影响范围很小，车轴和轮重间的应力叠加效应可以忽略．故本模型采用单侧双轮加载，车辆荷载采用JTG D64-2015《公路钢结构桥梁设计规范》所规定的疲劳荷载模型Ⅲ，双轮着地面积为600 mm×200 mm，单侧轴重为60 kN．

加载方式分为横向和纵向移动加载．横向加载方式见图3a)，记加载中心到节段模型横向中心轴的距离为ex，初始加载位置为ex=-600 mm(X负半轴)，随后以150 mm为一个加载步向X正向移动，最终当ex=600 mm时停止加载，一共九个工况，分别记为T1～T9．纵向加载方式见图3b)，记加载中心距离节段模型纵向中心轴的距离为ez，初始加载位置为ez=-3 750 mm(Z负半轴)，随后以150 mm为一个加载步向Z正向移动，最终在ez=3 750 mm处停止加载，共51个加载步．

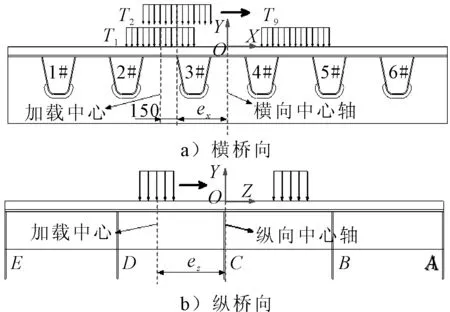
图3 移动荷载工况

1.3 关注节点的选取

弧形缺口边缘由于焊接操作会产生很大的残余拉应力，其与车辆荷载作用下所产生的压应力形成了拉-压循环，在面内外应力的共同作用下容易产生疲劳问题．U肋与横隔板的刚度差使得两者难以协调变形，在U肋与横隔板交接的焊缝处也很容易产生疲劳裂纹．由于模型和载荷的对称性，文中仅分析3#U肋处的疲劳细节，将横隔板两侧表面按Z轴指向分正负侧，关注点的选取见图4.

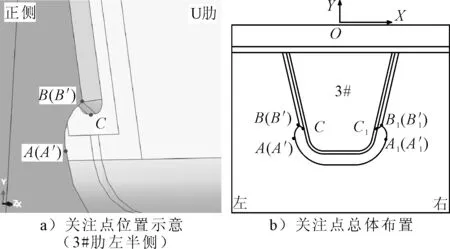
图4 关注点的选取

U肋两侧弧形缺口A和A’、A1和A’1节点，其中A’和A’1位于横隔板的负侧；横隔板-U肋焊缝处的横隔板焊趾，依次编号为B和B’、B1和B’1，其中B’和B’1位于横隔板的负侧；左侧U肋焊趾端部中点记为C，右侧U肋焊趾端部中点记为C1．

2 横隔板的变形影响分析

2.1 模型Ⅱ横隔板变形模式

以模型Ⅱ横、竖向加劲肋交接处D1点为起点，沿横隔板正负两侧表面竖直向上各布置一条路径，以顶板焊趾D3为终点．横隔板两侧的表面应力可视为横隔板面内应力和面外应力的叠加，二者又可以简化为膜应力和弯曲应力．基于T4工况下ez=-750 mm的载荷位置，提取两侧路径上的竖向表面应力，记S+和S-分别表示横隔板正、负侧路径上的表面应力，Sout为面外应力，Sin为面内应力，那么面外应力为：Sout=(S--S+)/2，面内应力可表示为：Sin=(S-+S+)/2．计算得出沿路径的横隔板面外弯曲应力，结果见图5．由图5可知：记应力值为0的节点为D2，则D1至D2段弯曲应力均为正值，D2至D3段弯曲应力均为负值，故D1至D2和D2至D3之间的横隔板弯曲方向相反，横向加劲肋上部的横隔板呈双向弯曲变形，见图6．

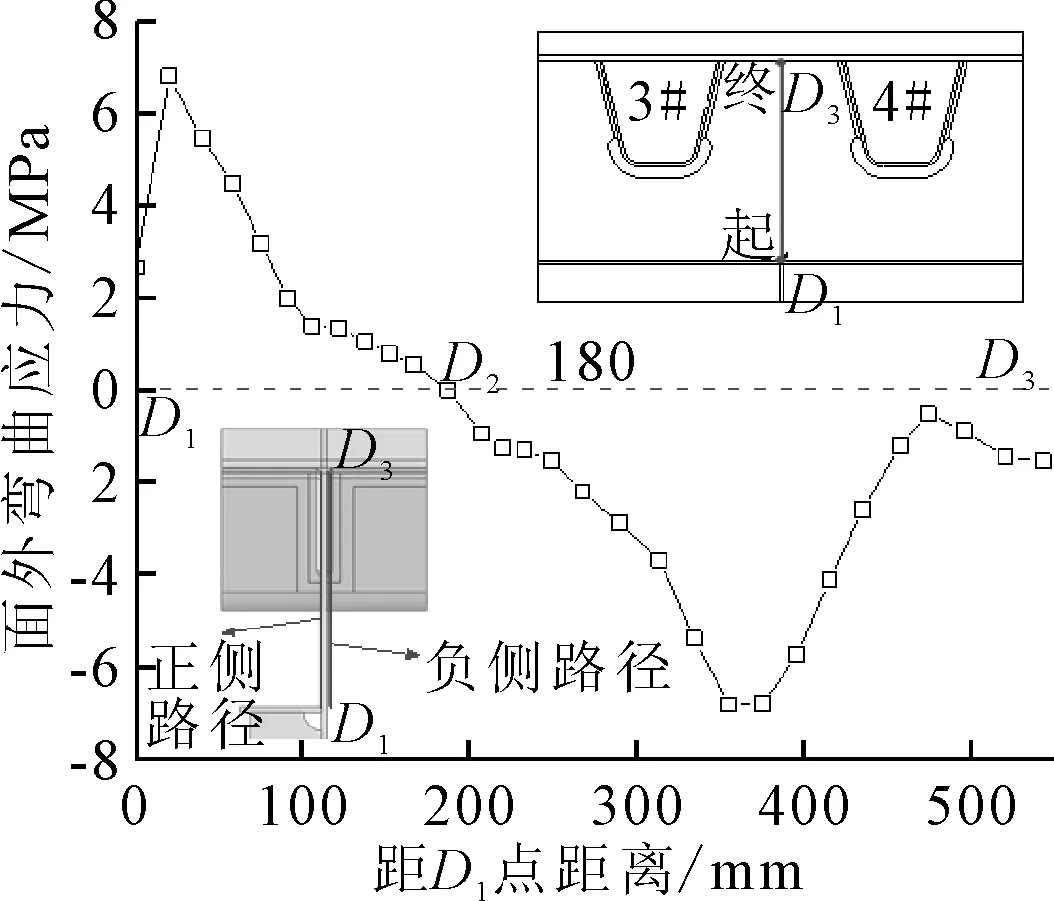
图5 沿路径横隔板面外弯曲应力

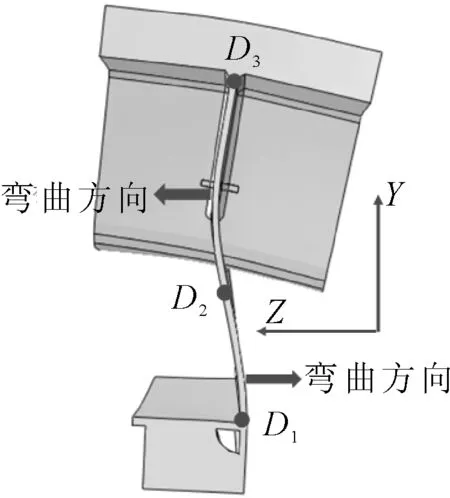
图6 模型Ⅱ横隔板变形

2.2 横隔板面内外变形影响分析

横隔板的总体面内、外变形程度可通过横隔板选定节点间的竖向和纵向位移差值来体现．提取两个模型在T4工况下D1与D2点的竖向和纵向位移变化曲线，分别计算D1与D2点间的竖向和纵向位移差值，结果见图7．由图7可知：模型Ⅱ的D1与D2点竖向位移差值与模型Ⅰ相比变化较小，但是纵向位移差值较模型Ⅰ大幅增加，且呈不对称分布，这是由于加劲肋的存在使得横隔板两侧自由挠曲受到约束造成的．因此，加劲肋的布置对横隔板面内变形影响较小，但会显著增加横隔板的面外变形，这与实桥测试结果一致．

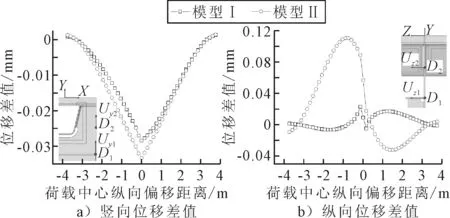
图7 各模型D1与D2之间的位移差值

3 疲劳细节应力与面内外变形影响分析

3.1 弧形缺口应力及面内外变形影响分析

3.1.1最不利荷载位置

提取两个模型3#U肋右侧弧形缺口细节在T1～T7工况下的主应力变化曲线，结果见图8．由图8可知：模型Ⅰ和模型Ⅱ的弧形缺口细节最不利荷载工况均为T4，即横桥向加载中心位于该细节正上方．两个模型的主应力变化曲线均成双峰形态，峰值均在ez=±300 mm处取得．因此，荷载纵向位于ez=±300 mm且横向作用于细节正上方时对两个模型的弧形缺口细节最为不利．

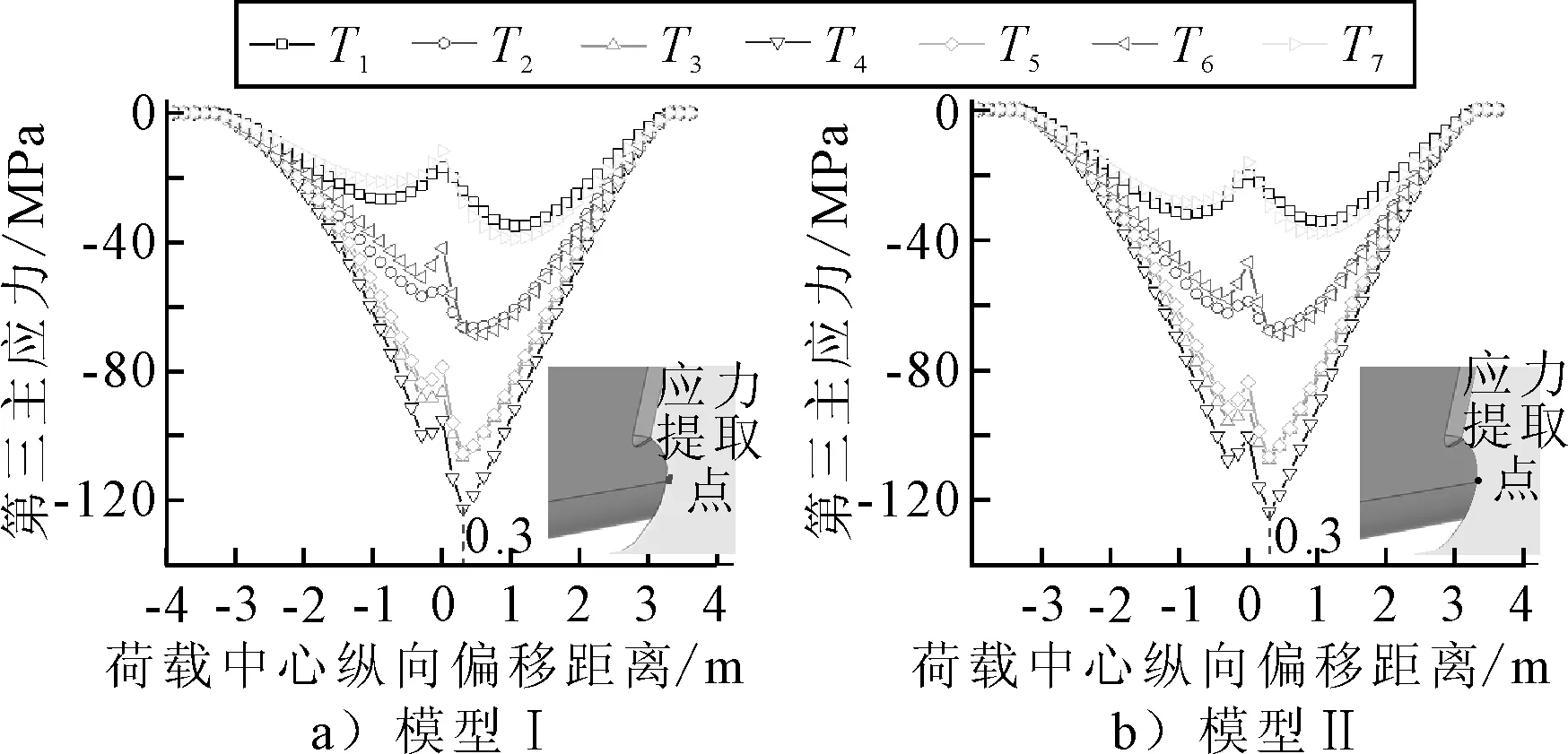
图8 弧形缺口第三主应力随荷载移动变化曲线

3.1.2弧形缺口疲劳节点的位置分析

以两个模型横隔板焊趾B1为起点，沿弧形缺口边缘创建长度为40 mm的路径．当荷载位于T4工况下ez=300 mm时，提取路径上的第三主应力，结果见图9．由图9可知：记距焊趾B1的距离为S，两个模型主应力分布曲线均在S=20 mm处取得最大值，故记距离焊趾20 mm处的节点为疲劳节点A1，其余三处疲劳节点位置与此一致．疲劳节点可以准确反映疲劳细节的受力特征，因此后文的应力和变形分析都是基于疲劳节点展开．

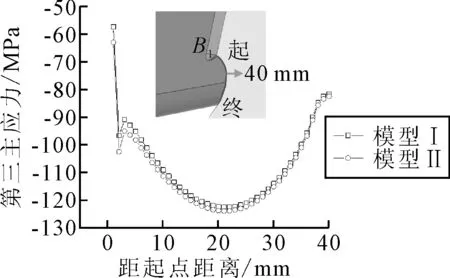
图9 弧形缺口路径第三主应力分布

3.1.3弧形缺口细节主应力影响分析

分别提取两个模型弧形缺口疲劳节点A、A’在T2工况下和A1、A’1在T4工况下的第三主应力变化曲线，结果见图10．由图10可知：两个模型的A、A1点主应力曲线基本一致，而模型Ⅱ的A’、A’1点主应力相较模型Ⅰ有所增加，但增加幅度较小．以右侧节点A’1为例，两个模型均在ez=-300 mm处取得主应力最大值，模型Ⅰ最大值为-125 MPa，模型Ⅱ最大值为-134 MPa，比模型Ⅰ高出9 MPa，仅增加了约7%．因此，横隔板加劲肋对弧形缺口细节的主应力影响较小．

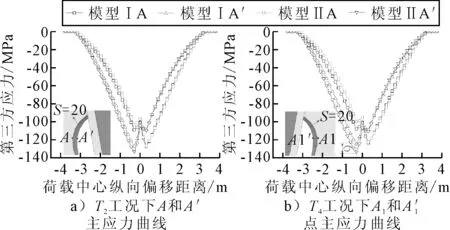
图10 弧形缺口疲劳节点第三主应力变化曲线

3.1.4弧形缺口细节变形影响分析

以两侧弧形缺口疲劳节点切线方向为X轴建立局部坐标系，分别提取两个模型A、A’点在T2工况下和A1、A’1点在T4工况下的切向表面应力SX变化曲线，分别由A和A’表面应力、A1和A’1表面应力计算出左、右两侧弧形缺口细节的面内应力和面外应力，结果见图11．

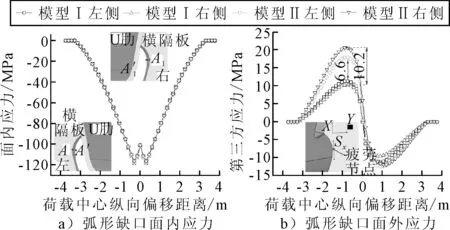
图11 弧形缺口面内外应力变化曲线

由图11可知：模型Ⅱ左、右两侧弧形缺口面内应力与模型Ⅰ基本相同，而面外应力相较模型Ⅰ大幅增加．模型Ⅰ和模型Ⅱ弧形缺口面外应力均在荷载位于ez=-750 mm处达到最大值，对于左侧弧形缺口细节，模型Ⅰ最大面外应力为11.4 MPa，模型Ⅱ最大面外应力为18.0 MPa，模型Ⅱ比模型Ⅰ高出6.6 MPa，增加了约58.6%；对于右侧弧形缺口细节，模型Ⅰ最大面外应力为10.4 MPa，模型Ⅱ最大面外应力为20.6 MPa，模型Ⅱ比模型Ⅰ高出10.2 MPa，几乎是模型Ⅰ的2倍，这同实桥测试结果一致．因此，横隔板加劲肋对弧形缺口细节的面内变形影响较小，但会大幅增加弧形缺口细节的面外变形．面外变形的增加会促进疲劳裂纹的诱发与扩展，故弧形缺口细节尤其是位于竖向加劲肋上方的细节疲劳性能大幅降低．

3.2 横隔板焊趾应力及面内外变形影响分析

3.2.1横隔板焊趾主应力影响分析

提取两个模型横隔板焊趾B1和B’1在T4工况下的第一和第三主应力曲线，结果见图12．由图12a)可知：两个模型的B1点第一主应力均在ez=-1 500 mm处取得最值，分别为24.5和50.2 MPa，模型Ⅱ几乎是模型Ⅰ的两倍．由图12b)可知：两个模型的B’1点第三主应力均在ez=-300 mm处取得最值，分别为-109.9 MPa和-139.7 MPa，模型Ⅱ比模型Ⅰ增加了27.1%．计算两个模型B1和B’1点应力幅值，结果表明模型Ⅱ的B1、B’1点应力幅值较模型Ⅰ分别增加了16.2%和28.1%．

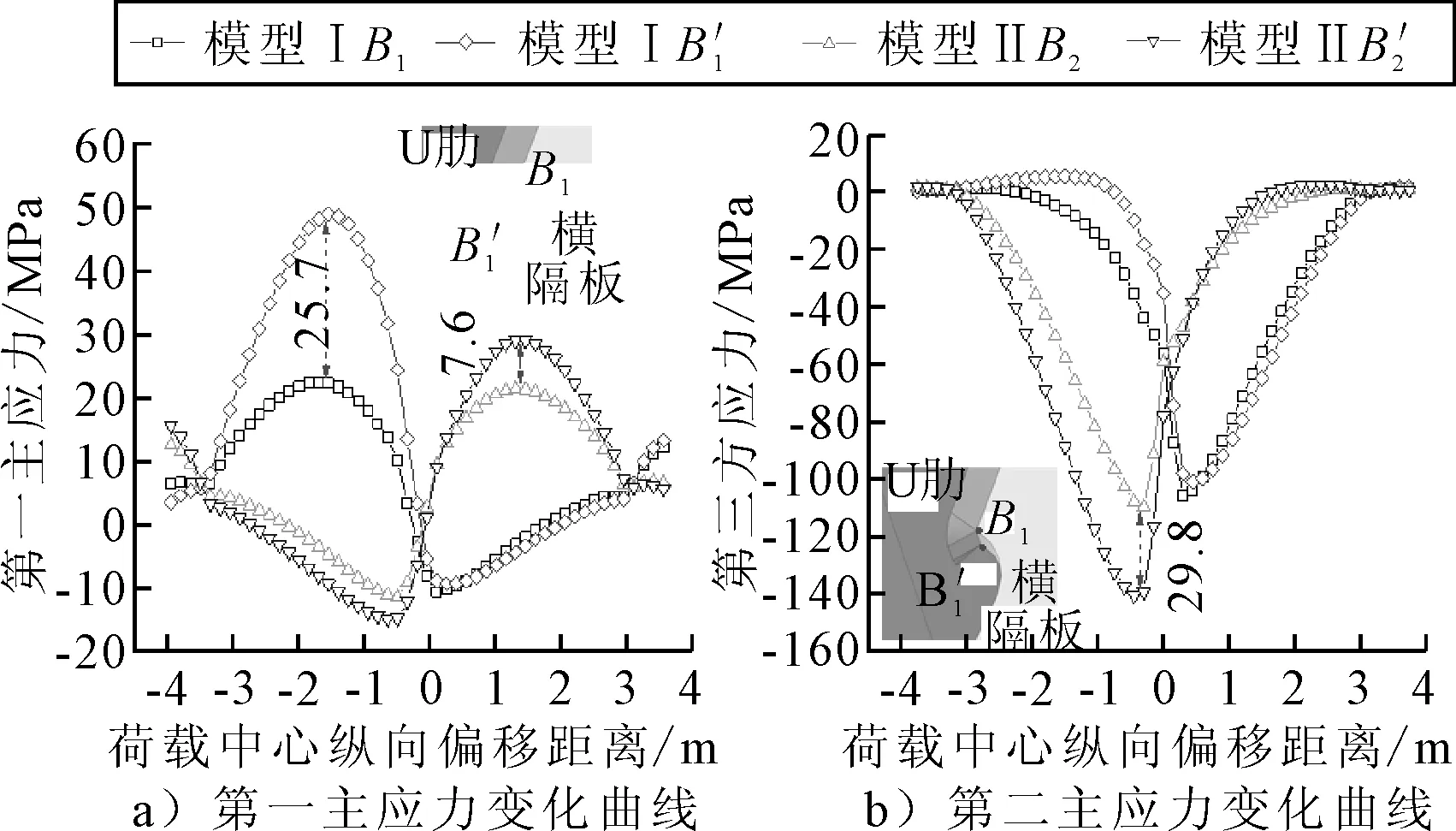
图12 横隔板焊趾主应力变化曲线

3.2.2横隔板焊趾面内外变形影响分析

以横隔板焊趾B和B’、B1和B’1为起点沿焊缝布置2组长为30 mm的路径．当荷载横向位于焊趾细节正上方且ez=300 mm时，提取两组路径上垂直于焊缝方向的表面应力，分别计算出左、右两侧沿焊趾路径的面内外应力分布，结果见图13．由图13可知：模型Ⅱ焊趾面内应力与模型Ⅰ相差较小，而模型Ⅱ焊趾面外应力较模型Ⅰ大幅增加．各焊趾路径面外应力均在距起点1 mm处取得最值，此时模型Ⅱ左侧焊趾面外应力约为模型Ⅰ的1.5倍；右侧焊趾面外应力约为模型Ⅰ的1.8倍，其主要原因是右侧焊趾靠近竖向加劲肋，受到的刚度影响较大．

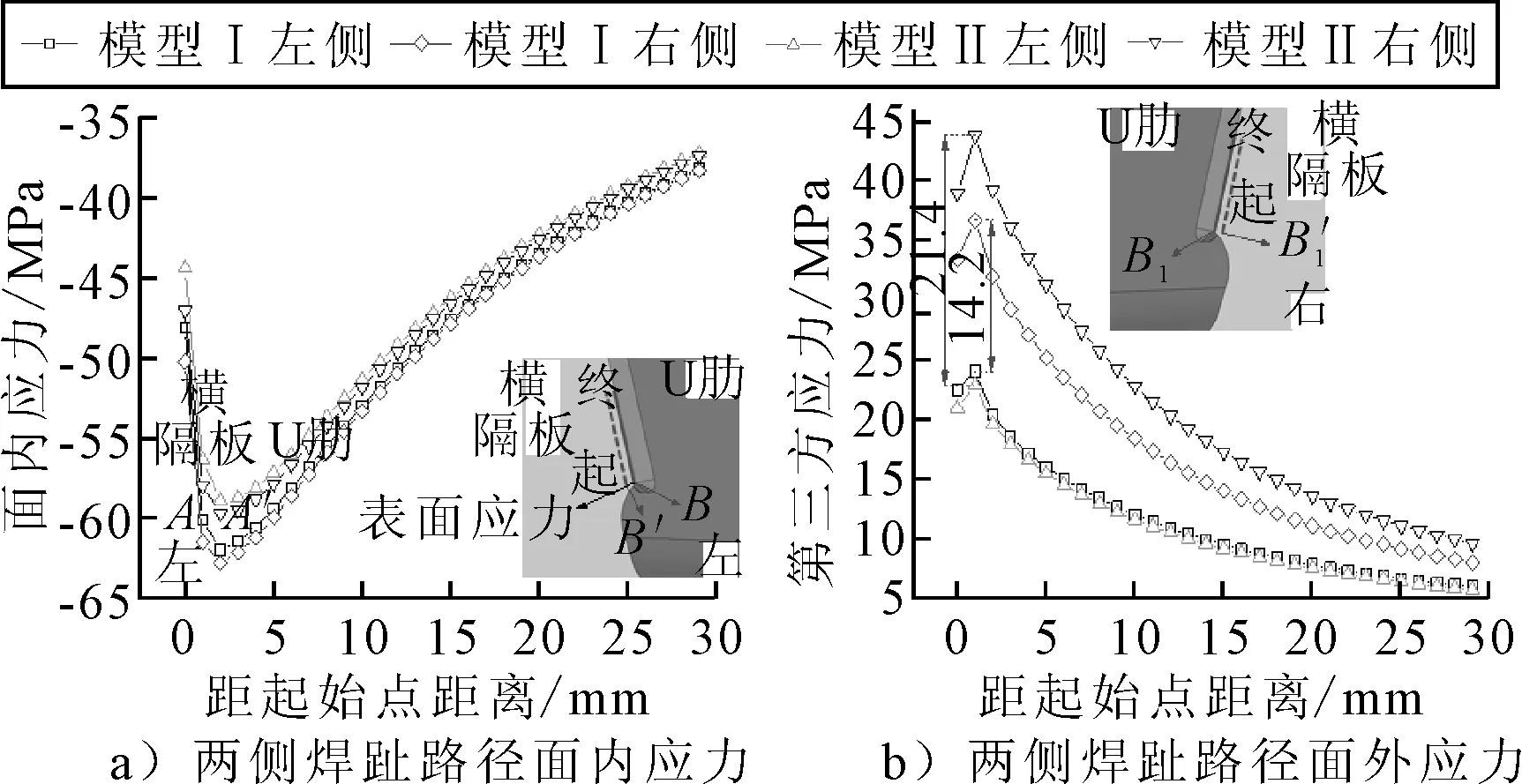
图13 两侧焊趾路径的面内外应力分布

3.3 U肋腹板焊趾应力及面内外变形影响分析

3.3.1最不利荷载分析

提取两个模型右侧U肋焊趾C1点在T1～T6工况下的第一主应力变化曲线，结果见图14．由图14可知：两个模型的C1点最不利荷载工况均为T2，即横向加载中心位于左侧U肋腹板正上方，且曲线均呈双峰对称分布，两个模型均在ez=±300 mm处取得主应力最大值．因此，U肋焊端最不利荷载位置为细节另一侧U肋腹板正上方车道且ez=±300 mm处．

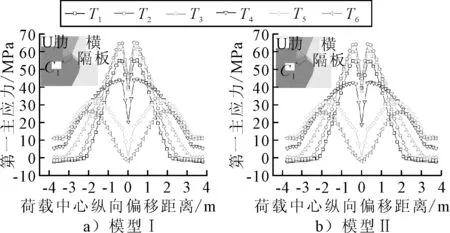
图14 C1点第一主应力变化曲线

3.3.2U肋焊趾表面应力影响分析

以两侧U肋-横隔板焊缝方向为X轴，以U肋-顶板焊缝方向为Y轴，分别建立局部坐标系．U肋焊趾端部水平裂纹的控制应力为腹板竖向外表面应力SX，自焊趾沿焊缝竖向扩展的裂纹控制应力为腹板纵向外表面应力SY．提取C和C1点的SX和SY值，结果表明SY相较SX较小，故竖向表面应力SX起主要控制作用．沿模型两侧U肋焊趾端部布置10 mm长的路径，分别记为外侧路径1、外侧路径2，在U肋腹板内侧表面对应上述外侧路径的位置各布置一条路径，分别记为内侧路径1、内侧路径2．提取外侧路径1、2在最不利荷载位置下的竖向表面应力SX，见图15．由图15可知：模型Ⅰ和模型Ⅱ两侧焊趾路径上的竖向表面应力分布曲线比较接近，说明横隔板加劲肋对U肋焊趾端部的表面应力影响较小．

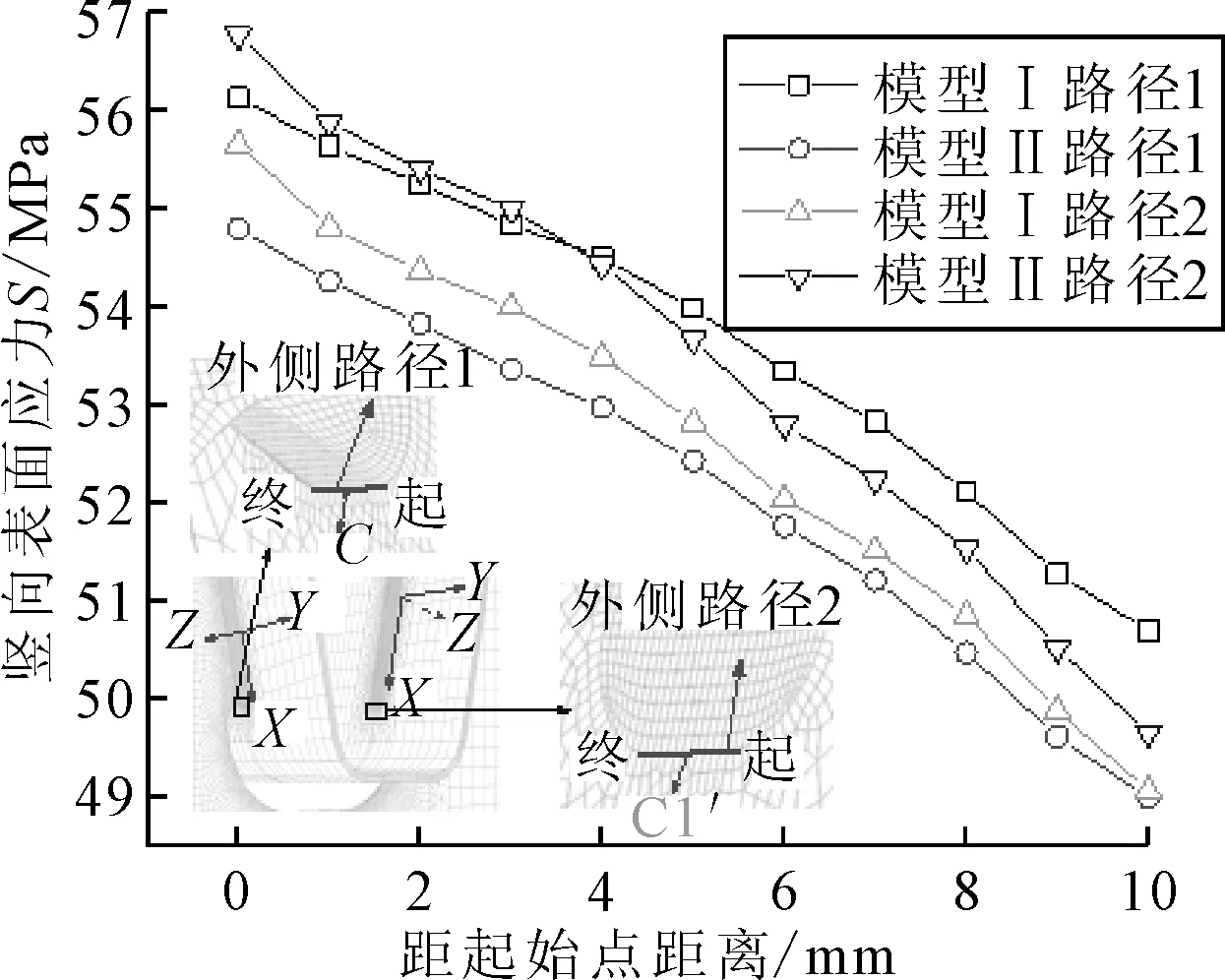
图15 沿外侧路径1和2竖向表面应力分布

3.3.3U肋焊趾变形影响分析

U肋腹板竖向表面应力同样可以视为面内应力和面外应力的叠加．当荷载位于T2工况下ez=300 mm时，提取内、外侧路径1和内、外侧路径2上的竖向表面应力，分别计算出左、右侧U肋焊趾端部的面内外应力分布，结果见图16．由图16可知：模型Ⅰ和模型Ⅱ两侧焊趾端部的面内应力和面外应力分布曲线趋势基本一致，且应力值相差较小．综上，横隔板加劲肋对U肋焊趾端部细节的变形影响较小．

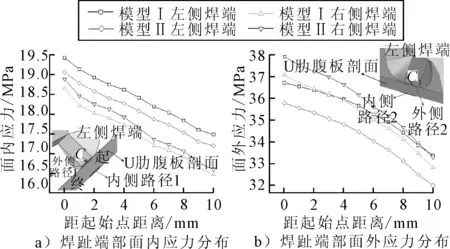
图16 沿焊趾路径面内外应力分布

4 结 论

1) 横隔板加劲肋显著增加了U肋下部横隔板段的面外变形，对其面内变形影响较小；对横隔板弧形缺口和横隔板焊趾细节的受力影响较大，对U肋焊趾细节的受力影响较小．

2) 加劲肋的布置对弧形缺口细节的主应力影响较小，但显著增加了设加劲肋侧横隔板焊趾的主拉应力和另一侧横隔板焊趾的主压应力，两侧横隔板焊趾细节应力幅值均增加，发生疲劳开裂的概率上升，在桥梁检测工作中要给予重视．

3) 位于竖向加劲肋上方的弧形缺口和横隔板焊趾细节的面外变形相较不设加劲肋时大幅增加，促进疲劳裂纹的萌生和扩展，在桥梁维护工作中要对这两个细节的开裂采取及时的补强措施．