爆炸载荷作用下仿玉莲脉络加筋板的动态响应分析
2022-07-11王勇辉
何 强,王勇辉,顾 航
(江苏科技大学 机械工程学院,镇江 212100)
军用舰船作为一种常规水上作战设施,很容易遭受各种武器的爆炸攻击.在爆炸载荷作用下,舰船结构较易发生大变形甚至破坏失效,从而丧失战斗能力.因此,舰船抗爆性能的提升对提高海军军事实力尤为重要.工程上经常采用在板材表面焊接钢筋(加筋板)的方式来确保军用舰船的抗爆性能.加筋板作为船体结构的重要组成部分,其抗爆防护性能是衡量舰船生存能力的重要指标,许多国内外学者通过理论、仿真及试验手段对其爆炸载荷作用下的动力响应进行了大量的研究.文献[1]比较了在矩形载荷、三角形载荷和指数形载荷作用下加筋板上各点的压力、等效应力和位移的变化情况,指出冲击载荷作用的时间越短,仿真破坏的效果越大,加筋板产生的塑性形变也越大;文献[2]对爆炸载荷作用下8种加筋模式金属板的抗爆性能进行了研究.结果表明随着加强筋数量的增加,塑性变形能在总能量中的占比逐渐降低,金属板整体抗爆性能增加.文献[3]研究了水下爆炸冲击作用下船用加筋结构的动态响应特性及其抗爆防护性能,研究发现肋板结构类型是影响加筋板变形响应速度及塑形变形幅值的重要因素;文献[4] 运用Abaqus对爆炸载荷作用下加筋钢板的动力响应进行了研究,确定了加劲板在考虑加劲肋结构影响时的动力响应;文献[5]研究发现在一定的爆炸冲击载荷作用下,加筋板的整体变形随着相对刚度的增大而减小;局部挠度与整体挠度之比则随相对刚度的增加而增大.文献[6]数值模拟了光板、双根加筋板、十字加筋板和双十字加筋板在爆炸载荷作用下的破坏变形情况,并通过试验证明Abaqus软件能较好地模拟真实爆炸情况.
近年来,越来越多的学者以自然界生物结构为原型设计出具有不同的仿生薄壁管,研究发现将生物结构特征引入到薄壁管的设计中可有效提高薄壁管的耐撞性[7-10].受此启发,文中以荷叶为生物原型,在分析荷叶叶脉生物学和力学特性的基础上,将叶脉分枝结构特性引入到传统薄壁圆板中,观察荷茎和叶的宏微观结构,获取主要结构和特征,并通过改变结构参数得到不同的仿荷叶脉络加筋板.进一步通过仿真分析研究其受爆炸冲击载荷作用下的动态学响应特性,以期提高普通圆板的抗爆性能.
1 仿荷叶脉络分枝加筋板结构设计
荷叶为睡莲科植物莲的叶,呈圆形或圆盘形,直径可达1 m左右,叶脉呈放射形网状.
如图1,荷叶叶脉特殊的构造规律造就了它强大的承载能力,实现对载荷的分割传递,使结构受力非常合理,能承受特别强的重力.荷叶叶脉从荷叶中心出发向四周蔓延,呈放射形网状.叶脉可以分主叶脉和次级叶脉,主叶脉粗壮,次级叶脉从主叶脉分叉向荷叶边缘交错倾斜延伸,且次级的断面尺寸向边缘逐渐减小.主叶脉承受了主要的载荷,次级叶脉使得靠近边缘部分的应力分布更加均匀,进一步加强靠近荷叶边缘部分的承载能力.
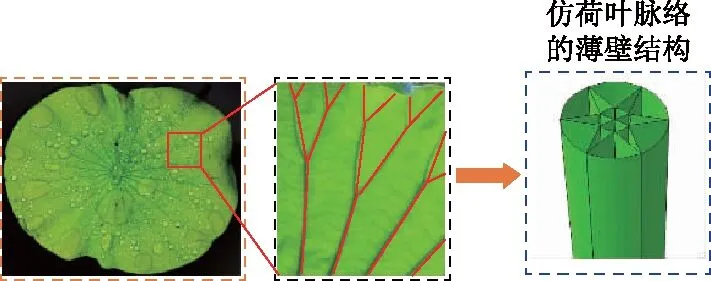
图1 仿荷叶脉络分枝加筋板几何构性
文中仿照荷叶脉络分枝特点,提出一种具有荷叶脉络分枝结构的仿生加筋板,并进一步研究了其受爆炸载荷作用下的力学行为.图2为仿荷叶脉络分布加筋板的几何特征和截面演变,Router和Rinner分别为圆板的半径、加强筋的内圆半径,tb为加强筋分支的厚度,tt为加强筋主干的厚度,N为沿圆周分布的主干数目.各分支在外面板板边缘相交,形成一个交叉点.定义加强筋结构参数γ为Rinner和Router的比值,α为tb和tt的比值,α具体的参数值如表1.规定圆板的半径Router等于500 mm,厚度为25 mm,加强筋的内圆半径随着γ的变化而变化;加强筋内圆的厚度为15 mm,高度为60 mm.
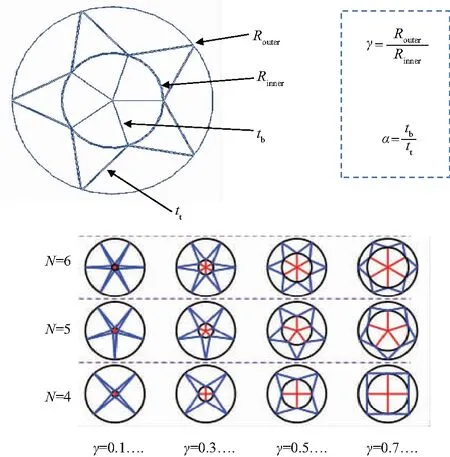
图2 仿荷叶脉络分布加筋板的几何特征和加强筋演变

表1 α具体的参数值
2 数值模型
2.1 仿荷叶脉络分布加筋板的有限元模型
运用显示非线性动力学分析软件Abaqus模拟爆炸冲击载荷作业下仿荷叶脉络加筋板的力学特性,计算模型如图3.爆炸载荷的施加采用Conwep算法,在距离加筋板面板中心上方150 mm处施加5 kg当量的TNT,炸药当量相应的比距离为:
(1)
式中:R为炸药距离中心的距离;W为TNT当量.
建模过程中,仿生加筋板的圆板采用实体单元,加强筋采用壳单元,加筋板边缘采用完全固定约束.
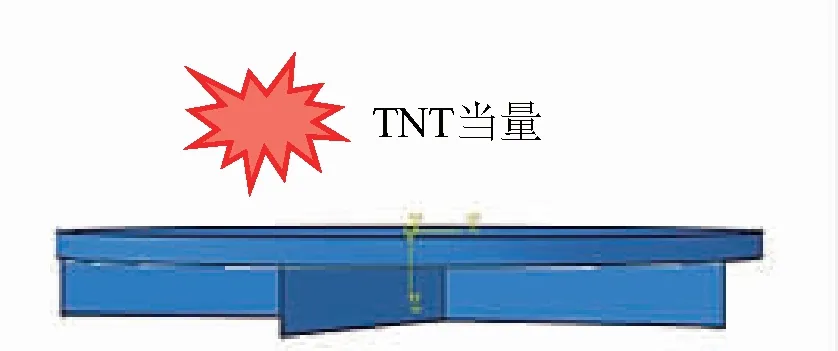
图3 仿荷叶脉络分布加筋板在爆炸载荷作用下的有限元模型
仿荷叶脉络分布加筋板的材料本构采用弹塑性模型进行描述,密度ρ=7 800 kg/m3,弹性模量E=200 GPa,泊松比ν=0.3.应力和应变率硬化采用了Johnson-Cook模型:
(2)
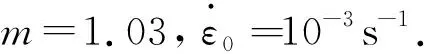
为了研究有限元网格大小对数值结果精确度的影响,列举了5种不同的网格大小进行仿真计算.图4为结构在5种不同网格大小中仿真的挠度-时间曲线,能够看出网格尺寸为10 mm×10 mm和15 mm×15 mm下的挠度-时间曲线比较接近,误差非常小.网格变密会大幅度增加计算成本.因此,综合考虑计算成本和计算效率,将网格尺寸选定为10 mm×10 mm.
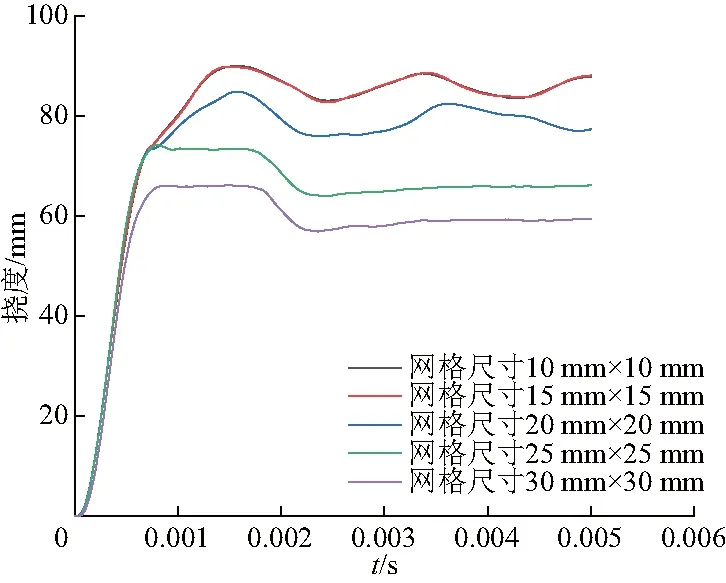
图4 不同网格大小新型结构的挠度-时间曲线
2.2 建模方法验证
为验证该模型的可靠性,采用与参考文献[12]中3 mm板相同的结构参数、截面属性和材料参数,在无限制的爆炸配置下,在与实验一样的爆距处采用Conwep算法施加相同当量的TNT,分别计算了不同TNT当量下的背板挠度.如图5,将有限元模型仿真的结果和实验结果对比,结果发现仿真计算结果与实验结果、仿真变形模式与实验变形模式吻合较好.由此可知,所建立的有限元模型能够准确地模拟结构受爆炸载荷作用下的变形,并在此基础上进一步对不同结构参数仿荷叶脉络加筋板在爆炸载荷下的力学行为进行研究.
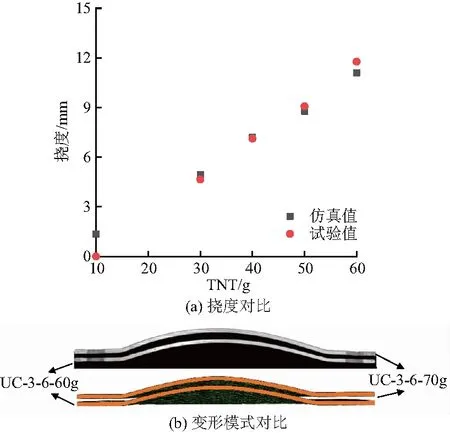
图5 实验结果与仿真结果
3 爆炸载荷下的动力响应分析
3.1 仿生加筋板的变形模式
为了研究仿生加筋板在爆炸载荷作用下的变形模式,选用参数N=4,α=1,γ=0.3的仿生加筋板,并且在150 mm距离施加5 kg当量的TNT.在爆炸过程中,网格会发生很大的变形,甚至会发生畸变,整个系统可能出现较高的沙漏能量;如果沙漏能较高,计算结果是不可靠的,因此有必要对仿生加筋板的能量项进行研究分析.图6是仿生加筋板能量项与时间的曲线图,伪应变能或沙漏刚度是用来控制沙漏变形的能量,AE是伪应变能,IE是总内能,KE是动能,PD是塑性耗散能,SE是储存的应变能.从图中发现炸药爆炸后动能KE迅速增大,随着冲击波的消散,动能逐渐减小;塑性耗散能上升到一个平台后再次上升,从动能曲线可以看出,塑性耗散能的第二次上升发生在仿生加筋板到达最大位移处弹回并向相反方向运动的时刻,所以第二次上升是由于回弹引起的塑性变形.伪应变能(AE)15.34 kJ大约为总内能(IE)262 kJ的5.9%,说明计算结果稳定可靠.
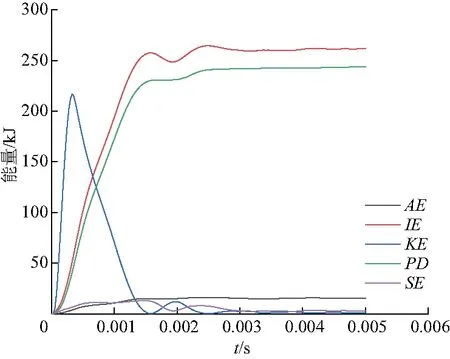
图6 仿生加筋板能量项与时间的曲线图
炸药爆炸后,不同时刻仿生加筋板的变形模式和应力分布云图如图7.

图7 不同时刻仿生加筋板的变形模式和应力分布云图
仿生加筋板的响应过程可以分为3个阶段:冲击前、冲击中、冲击后.冲击前,TNT在源点爆炸,此时并没有与仿生加筋板产生相互作用.冲击中,爆炸冲击波和仿生加筋板的面板产生相互作用,最后冲击波与面板的接触力减小至零.冲击后,爆炸冲击波与面板的接触力为零,但仿生加筋板在惯性作用下继续发生形变.当面板中心挠度达到最大值后,仿生加筋板出现反弹.从应力分布云图可以看出,爆炸冲击波首先作用在仿生加筋板的中心,面板将载荷传递给加强筋的主干,主干再将载荷分散给分支.在爆炸载荷进一步作用下,面板塑性变形区域逐渐扩大,轴线方向上向四周扩展,径向方向上四周侧边受拉力作用向中心运动,最终形成一个沙漏状塑性变形区.5 000 us时,加强筋的主干发生明显的弯曲变形,分支则向图中所示a方向产生轻微的弯曲形变.
3.2 仿生加筋板沿轴方向的挠度分布
为进一步深入地了解仿生加筋板的变形机理,对受拉伸和弯曲作用产生的轴向位移进行研究.如图8,在板面沿着X轴选取5个点,分别命名为A1、A2、A3、A4、A5.其中A1为迎爆面中心点,点A1、A2、A3、A4、A5分别间隔100 mm.从图9(a)可知,A3沿X轴的位移值最大,其余各单元的位移值随着距A1点处距离的增大而增大.A2、A3、A4在炸药爆炸后迅速到达了最大位移,而A5比A2、A3、A4滞后.A4的位移值3.13 mm和A5的位移值3.10 mm相比A3的位移值3.27 mm分别相差4.4%、5.4%,而A2的位移值2.38 mm差值高达27.2%.这是因为点A2刚好处于加强筋的主干上,刚度大不易发生拉伸变形.从图9(b)可知,A1处的挠度值最大,其余各单元的挠度值随着距A1点处距离的增大而减小.A1、A2、A3、A4、A5处的运动速率先增大后减小,随着时间的增大,A5处的运动速率一直较小.
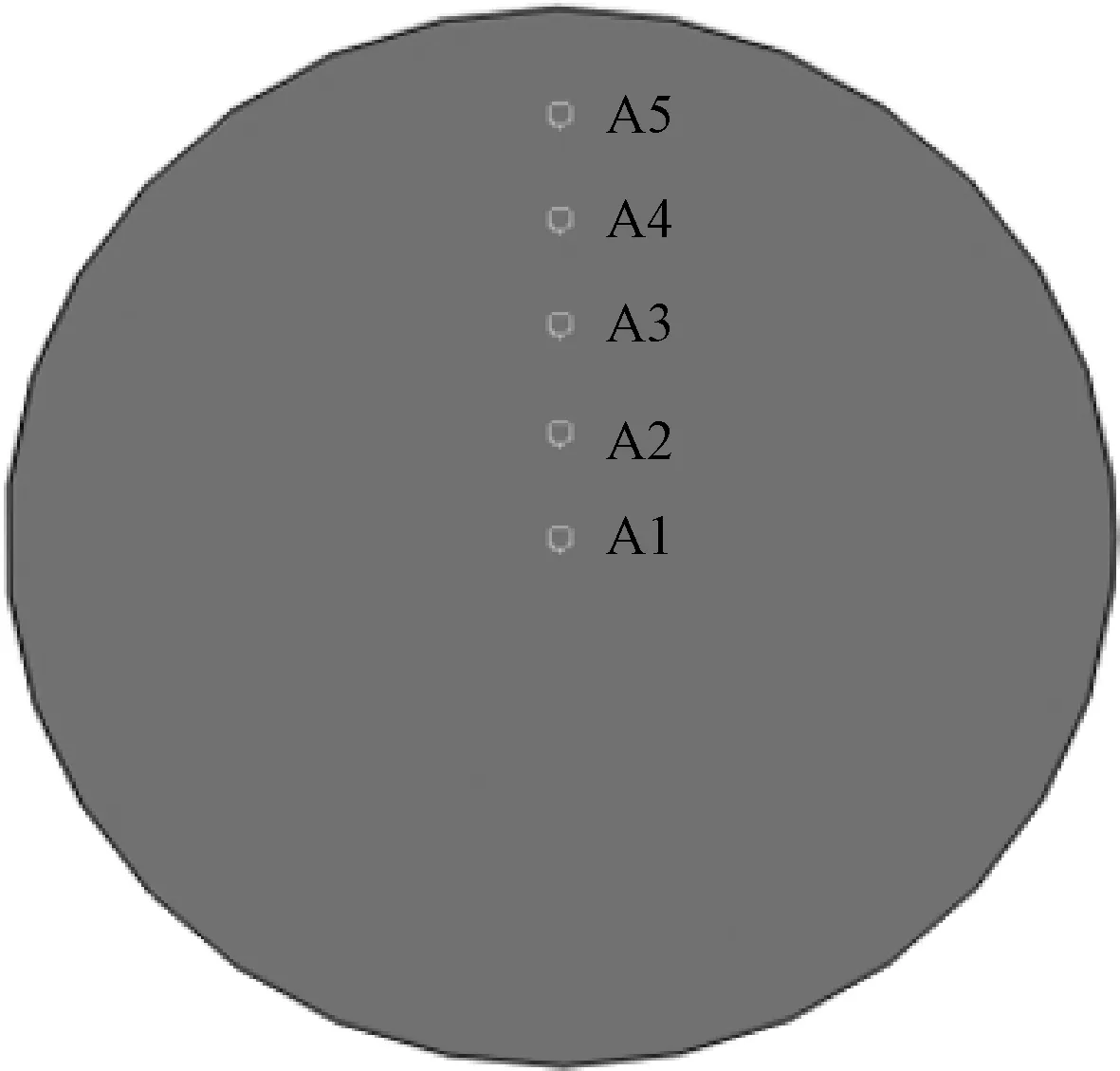
图8 各点位置分布图
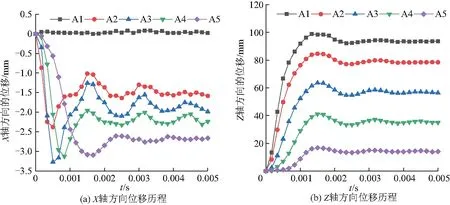
图9 各点沿轴向的位移值
3.3 仿生加筋板与传统加筋板的对比分析
图10是等质量的仿生加筋板和传统加筋板、光板在150 mm距离施加5 kg当量的TNT下的挠度-时间曲线和塑性耗能柱形图.
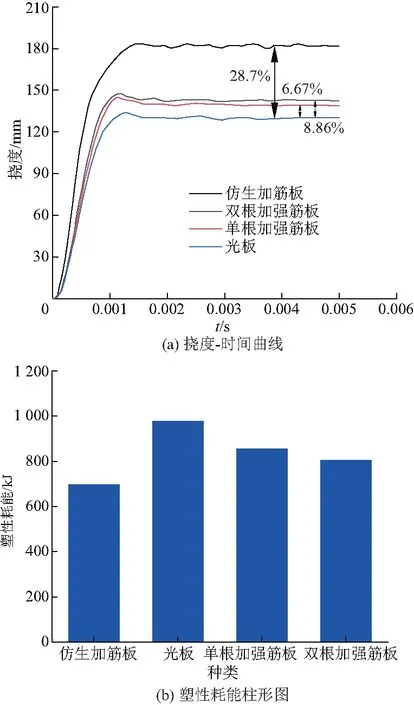
图10 挠度-时间曲线、塑性耗能柱形图
从图10可以看到,挠度值在短时间内快速升高,最后都趋于平稳;仿生加筋板中心点最终挠度比光板、单根加强筋板和双根加强筋板分别减少28.7%、6.67%和8.86%.如塑性耗能柱形图,仿生加筋板的整体塑性耗能745.9 kJ比光板的整体塑性耗能997 kJ减少251.1 kJ,减小约49%,同时也都低于单根加强筋板和双根加强筋板的整体塑性耗能.说明将叶脉分枝结构特性引入到传统薄壁圆板中得到的仿生加筋板比传统加筋板有着更好的抗爆性能.
3.4 比值α、γ对仿生加筋板抗爆性能的影响
图11是在不同主干数目N下,结构参数γ和仿生加筋板中心挠度的关系,图中可以看出,对于所有不同主干数目的仿生加筋板,在分支与主干厚度之比α等于0.5或1时,随着结构参数γ增大,仿生加筋板中心的挠度先减小后增大;在分支与主干厚度之比α等于1.5时,随着结构参数γ增大,仿生加筋板中心的挠度随之增大.对于所有不同主干数目的仿生加筋板,挠度值随比值γ的变化趋势相同,当结构参数γ<0.2时,随着α的增大,挠度值逐渐减小;当γ>0.2时,挠度值随着α的增大而增大.特别的是随着主干数目N的增大,在0.2<γ<0.5时,随着α值的变化,挠度值变化值逐渐增大,总体上差值变化不大.
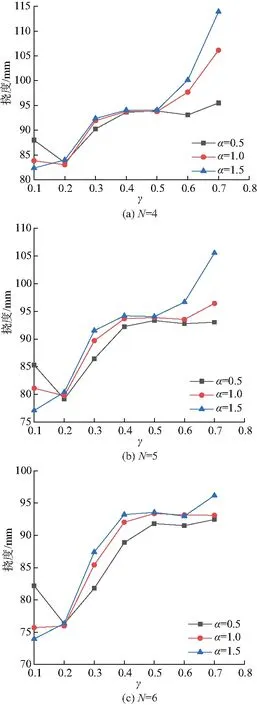
图11 不同结构参数和壁厚比α对加筋板挠度的影响
图12为N=5,α=0.1时,不同比距离下,仿生加筋板结构参数γ对其抗爆性的影响.图中可以看出,在不同的比距离下,结构参数γ都呈现相同的趋势,挠度值先减小后增大,在γ=0.2时,挠度值最小,说明比值α、γ对仿生加筋板的抗爆性能有着重要影响,α等于0.5或1时,γ=0.2的仿生加筋板有着更好的抗爆性; 0.2<γ<0.5时,α对仿生加筋板抗爆性的影响随着主干数目N的增大逐渐减小;特别是主干数目N=4的时候,0.2<γ<0.5时,α对仿生加筋板抗爆性影响较小.
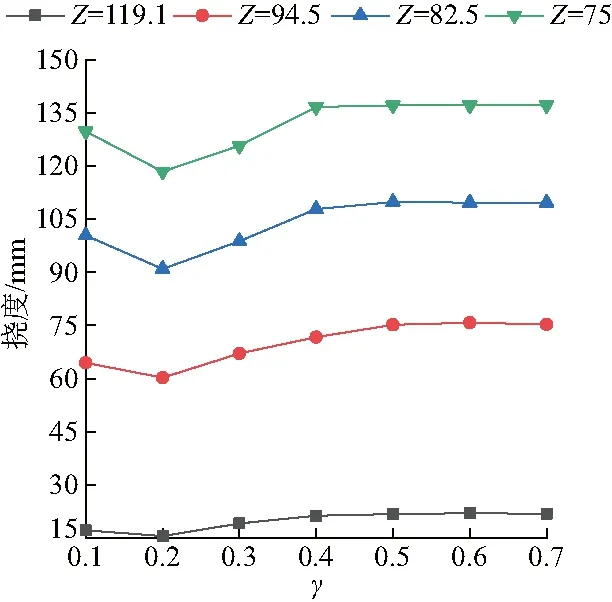
图12 不同比距离下结构参数γ对加筋板挠度的影响
3.5 主干数目N对仿生加筋板抗爆性能的影响
为了研究主干数目N对仿生加筋板抗爆性能的影响,设计了7个案例,每个案例中有3种结构.图13为3种不同主干数目的仿生加筋板挠度值和塑性耗能,结果表明当仿生加筋板的主干数目N改变时,a6和a9的挠度值变化较为显著,随着N的增大呈递减趋势;相对应的塑性耗能随着主干数目N的增大而减小.除a6、a9外的其它案例,当N变化时挠度值的变化不明显,其相对应的塑性耗能变化较为明显,且随着N的增大而减小.
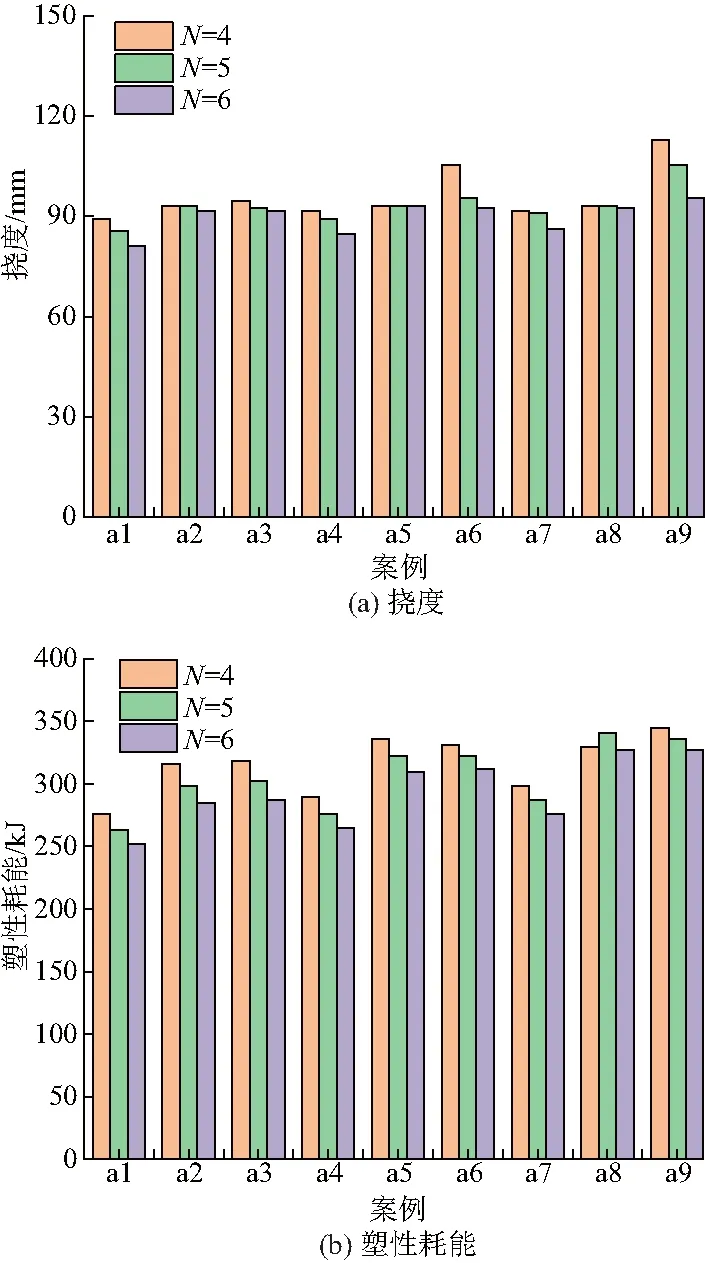
图13 不同主干数目N的仿生加筋板的挠度值和塑性耗能
说明在这些案例中,增加仿生加筋板的主干数目,增强其抗爆性能不明显,但能显著提升它的吸能特性.
3.6 比距离Z对仿生加筋板抗爆性能的影响
为研究比距离Z对仿生加筋板抗爆性能的影响,选用N=6,α=1,γ=0.1的仿生加筋板.在爆距一定的情况下,设计了10种依次减小的比距离,将其对应的挠度-时间曲线进行对比.图14为不同比距离下仿生加筋板的挠度-时间曲线和最终挠度值,从图14(a)中可以看到,仿生加筋板在炸药起爆后20.4 us后开始变形,随后面板到达最大值;位移到达最大值之后,仿生加筋板有小幅度的回弹和振荡;随着比距离的增大,这种回弹的幅度越大.如图14(b),仿生加筋板的最终挠度值随着比距离的增大而减小,挠度值增长率随着比距离的增大而增大,说明通过减小比距离,可以降低面板回弹的幅度;随着比距离的减小,比距离对仿生加筋板抗爆性能的影响越小.
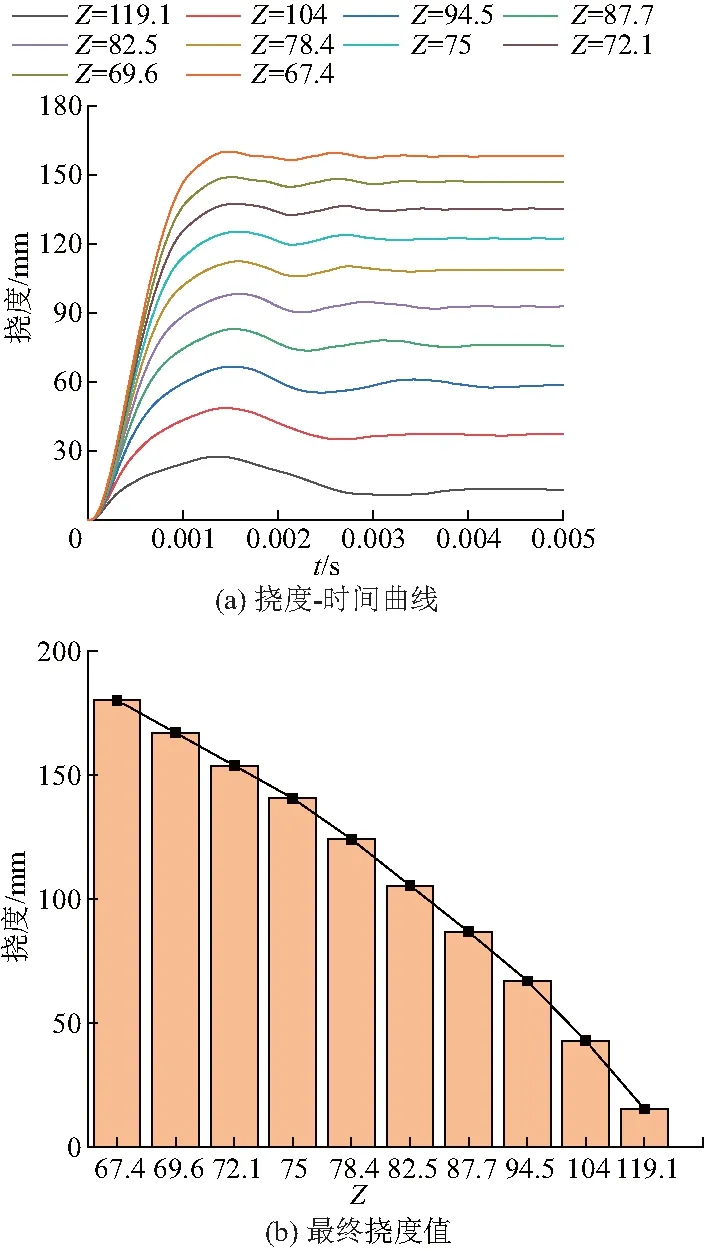
图14 不同比距离下仿生加筋板的挠度-时间曲线和最终挠度值
4 结论
根据荷叶脉络的分布特性,提出一种具有主干分支结构的仿生加筋板.基于非线性动力学软件Abaqus,对爆炸载荷作用下仿生加筋板的动态响应进行研究.研究结果表明:
(1) 将叶脉分枝结构特性引入到传统薄壁圆板中得到的仿生加筋板比传统加筋板有着更好的抗爆性能,其最终挠度比光板、单根加强筋板和双根加强筋版分别减少28.7%、6.67%和8.86%.
(2) 比值α、γ对仿生加筋板的抗爆性能有着重要影响,α等于0.5或1时,γ=0.2的仿生加筋板有着更好的抗爆性;0.2<γ<0.5时,α对仿生加筋板抗爆性的影响随着主干数目N的增大逐渐减小;特别是主干数目N=4的时候,0.2<γ<0.5时,α对仿生加筋板抗爆性影响较小.
(3) 仿生加筋板的主干数目N对其抗爆性能有一定的影响,增加仿生加筋板的主干数目N,可以提升它的吸能特性,但抗爆性能提升不显著.
(4) 比距离Z对仿生加筋板的抗爆性能有着重要影响,通过减小比距离,可以降低面板回弹的幅度;随着比距离的减小,比距离对仿生加筋板抗爆性能的影响越小.
