考虑电压稳定性与分布式电源接入的低压配电网无功优化研究

史可鉴,李胜川,朱义东,张新宇,刘 丹

(1.国网辽宁省电力有限公司 电力科学研究院，沈阳110000 ) (2.辽宁电能发展股份有限公司，沈阳110000)

随着时代的发展，人们对高质量电能的需求越来越大.近年来，传统的发电产能难以满足日益增长的使用需求，同时传统能源发电存在严重的环境污染问题[1].为解决以上问题，世界各国大力发展分布式电源，充分利用可再生能源发电.目前，我国各种类型的分布式电源逐步接入到配电系统中，缓解了能源紧缺问题，但同时分布式电源的高渗透率使得传统配电网运行面临严重的技术挑战[2].

分布式电源具备清洁、投入少等[3]众多优势，是我国智能电网建设的重要部分之一.在配电网中，分布式电源的接入可为配电系统提供供电助力，但同时它也会改变传统配电网的原有结构，从而使配电网中的潮流方向发生改变，进一步增加网络损耗和电压越限的风险，甚至使配电网中出现逆潮流问题[4].无功优化是解决以上问题的重要方法之一.它可以通过调节无功控制设备的工作方式，使系统运行过程达到最优效果，形成最优潮流.

近年来，针对配电网的无功优化问题，国内外学者展开了广泛研究.文献[5]考虑在分布式光伏影响下使得配电网的线损最小和电压偏差最小的多目标无功优化问题，并采用改进的粒子群算法求得了Pareto最优解，得到了一种组合无功控制策略.文献[6]建立的多目标模型综合保证了经济性和安全性，具体体现在以运行成本最小、线损最小以及电压偏差最小为3个目标函数，其求解算法在传统人工蜂群算法基础上加入高斯变异和混沌扰动，最终有效降低了成本和网络损耗.文献[7]考虑了分布式电源的输出功率特性，并采用改进的退火粒子群融合算法作为主要求解手段成功求得该多目标优化数学模型的最优解.文献[8]建立的配电网无功优化模型以有功线损最小辅以电压偏差惩罚函数为目标函数，利用改进遗传算法求解了该模型.现有文献大多建立单目标或多目标的优化模型，而对目标函数中各个评价指标的权重并未进行具体客观地分配，且对电压稳定性的分析较少.在求解方法方面，所用智能算法在求解优化模型的过程中存在着寻优结果不理想的情况.

因此，文中从系统安全性出发，以线损最小和电压质量最高为目标函数建立配电网无功补偿优化模型.目标函数中线损、电压越限和电压稳定性3个指标的权重采用变异系数法确定，该方法可根据相关数据提供针对性的客观权重.同时针对粒子群算法等智能算法[9-10]出现的求解陷入局部最优的情况，提出采用蜻蜓算法[11-12]应对该缺陷，得到全局最优解.所提供的高精度补偿方案，能降低线损、提高节点电压，进而保证电网安全运行.

1 配电网无功优化数学模型

从安全性角度出发，以线损最小和电压质量最高(包括电压偏差最小和电压稳定性最高)最为目标函数，建立了配电网无功优化模型，模型中充分考虑到了分布式电源加入后引起的约束条件变化.

1.1 目标函数

目标函数中考虑的3个指标分别为线损、电压偏差和电压稳定性指标.

(1) 线损：

式中：W为该区域配电网的所有支路合集；gk为支路k的电导，Ui和Uj分别为节点i和j的电压幅值；θij为节点i和j间的电压相角差.

(2) 电压偏差：

(3) 电压稳定性指标：

电压是否稳定影响着配电网能否正常运行，因此采用第一类电压稳定指标[13]作为配电网电压稳定性的评价项.对于从节点i到节点j的支路，该支路的电压稳定指标表示为：

式中：Pj+jQj为流过节点j的负荷；Rij+jXij为支路阻抗.对于整个配电网，定义L=maxLij来表示其稳定性，L值越小，表示配电网稳定性越好.

为了保证配电网地安全运行，以最小化线损、电压偏差以及电压稳定性值作为目标函数，表示为：

minaPloss+bΔU+cL

(1)

式中：a、b、c分别为各指标的权重系数.鉴于文献[5-8]对于权重的考虑过于主观，导致模型对特定应用场景的适应性较差，加之在该问题中，各指标的值具有波动性，文中采用变异系数法来给以上3个指标进行客观赋值[14]，利用现场数据对各指标进行针对性地赋值计算，增加了模型与实际问题的适配度.具体体现为当各指标现有值与目标值差距较大时，说明该指标较难实现目标值，应该赋予较大的权重，反之则应该赋予较小的权重[14].在无功优化问题中变异系数法的应用使得模型参数适配性更高，以达到更好的补偿效果.

n个时间状态下，线损的平均值和标准差为：

变异系数vP为：

电压偏差和电压稳定性指标的变异系数为：

最终，各指标的权重计算为：

式中：a、b、c分别为线损、电压偏差以及电压稳定性指标的权重系数.

1.2 约束条件

调节变压器和放置无功补偿设备(电容器)是当前配电网无功补偿的两种主要方式.文中由于包含了分布式电源，因此无功补偿方式主要由分布式电源的无功出力和添加无功补偿设备组成.在优化模型中，分布式电源的影响具体体现为在潮流计算中引入了分布式电源输出的有功功率和无功功率，进而影响配电网的节点电压及潮流情况.

潮流约束：

(2)

(3)

Pi=PDGi-PDi

(4)

Qi=QDGi-QDi+QCi

(5)

式中：Pi和Qi分别为节点i的注入有功功率和无功功率；PDi和QDi分别为节点i的负荷功率；PDGi和QDGi为节点i处引入分布式电源的有功功率和无功功率.

控制变量:

(6)

(7)

式中：QCi为第i个无功补偿装置的无功出力.

状态变量：

(8)

2 基于蜻蜓算法的模型求解

蜻蜓算法(dragonfly algorithm，DA)是2016年提出的一种新的群体智能优化技术[11]，可分为开发和探索两个基本阶段.在开发阶段，蜻蜓在某个区域内沿着一个方向飞行狩猎；在探索阶段，蜻蜓以静态群的形式在不同区域间飞行[11].总之，所有个体为了生存都应该被食物吸引以及被天敌驱散.

与粒子群算法等其它智能算法相比，蜻蜓算法在优化过程的最终阶段，蜻蜓的邻域面积会不断增加至整个搜索面积，以保证最后收敛到全局最优，提供高精度的最优解.而在配电网无功优化方案的制定上，高精度最优解的提出可以达到更好的优化效果，因此将蜻蜓算法应用在该问题的求解中.

蜻蜓算法对于配电网无功优化模型，即式(1～8)，求解过程如下：

(1) 初始化参数：在约束范围内初始化蜻蜓的位置，即无功补偿量的初始值QC，以及步长向量ΔQC,并计算初始目标函数值，设置最大迭代次数T.

(2) 对种群内每个蜻蜓个体进行分离、对齐、凝聚、捕食以及躲避天敌行为的相关计算，并自适应的调整各项行为的权重系数.

分离是指蜻蜓个体与邻居中其他蜻蜓个体之间保持距离以避免发生静态碰撞.

(9)

式中：QC为当前蜻蜓的位置；QCj为相邻第j个蜻蜓的位置；N为相邻蜻蜓个体的数量.

对齐表示蜻蜓与邻居中其他蜻蜓个体的速度要进行匹配.

(10)

式中：Vj为第j个相邻蜻蜓个体的速度.

凝聚指蜻蜓倾向于邻里蜻蜓的中心.

(11)

式中：QC是当前蜻蜓的位置；QCj为相邻第j个蜻蜓的位置；N为相邻蜻蜓个体的数量.

聚集捕食猎物：

(12)

分散躲避天敌：

(13)

分离、对齐、凝聚、捕食猎物以及躲避天敌综合影响每个蜻蜓个体的位置更新，具体体现在步长向量的变化中.

(3) 更新当前迭代次数的步长向量和位置向量，按约束条件对控制变量QC进行调整，修正越界的状态变量Ui.

步长向量为：

ΔQCt+1=(sSi+aAi+cCi+fFi+eEi)+wΔQCt

式中：t为迭代次数；s、a、c、f、e分别为以上5种行为的权重，其初始值是根据作者意愿随机选取的，且在迭代过程中随最优解的情况发生自适应变化.

蜻蜓个体位置向量的更新根据是否具有邻近解分为两种情况：

① 当存在邻近解时：

QCt+1=QCt+ΔQCt+1

② 当不存在邻近解时，蜻蜓需要使用随机游动在搜索空间中飞行：

QCt+1=QCt+Levy(d)*QCt

式中：t为当前迭代次数；d为位置向量的维数;Levy(d)为Levy(d)飞行方程：

式中：r1、r2为[0,1]中的两个随机数；β为一个常数，一般取1.5.

Γ(x)=(x-1)!

(5) 终止条件判断：若蜻蜓算法达到最大迭代次数T，则执行步骤(6)，若不满足，则回到步骤(2)；

蜻蜓算法流程如图1.

图1 蜻蜓算法流程

3 算例分析

为验证所提模型及算法的有效性，选择如图2的改进后IEEE 33节点系统进行仿真验证.该测试系统具有33个标准节点，在8、25、32节点处引入了分布式电源，并假设分布式电源的有功出力为150 kW，无功出力为0.

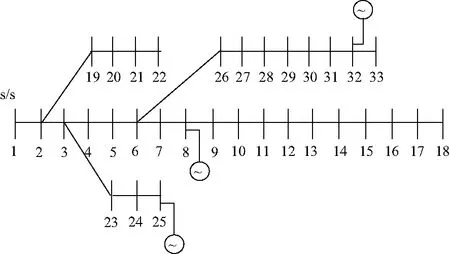
图2 改进的IEEE 33节点配电系统

另外，每个节点均可作为无功补偿点，其中无功补偿设备容量为0.1MVar×33，若在补偿方案中某个节点处补偿容量为0，说明该节点无需进行无功补偿.无功补偿装置为电容器.其中网络总负荷为3 715 kW+j2 300 kVar，额定电压为12.66 kV.目标函数中各指标权重系数a、b、c依次取20、5、1，节点电压Ui的约束范围为0.85～1.05 p.u.，无功补偿量QCi的约束范围为0～0.1 MW.

在Matlab 2014环境下进行仿真测试，得到补偿前后的系统线损和节点电压对比图(图3，4).

图3 DA补偿前后的系统线损对比图

图4 DA补偿前后的节点电压对比图

从图3可以看出，在DA优化算法求解下，对于各个节点，进行无功补偿后，系统线损都有明显的降低.从图4可以看出，节点电压也都得到了显著提高，且满足0.85～1.05 p.u.的约束范围，有效避免了欠电压情况的出现，提高了电压合格率，进而保证了供电质量和安全.

为了充分验证蜻蜓算法在解决上述配电网无功优化问题的有效性，将传统算法粒子群算法(particle swarm optimizationm，PSO)和遗传算法(genetic algorithm，GA)引入作对比分析.其中各算法的迭代次数统一为200.GA的种群数量为20，交叉率为0.01，变异率为0.001；PSO的种群数量为20，加速因子为0.1，惯性权重为0.1.对比结果见表1.

表1 智能算法优化方案对比结果

由表1结果对比可知，相比于传统算法，在降低线损方面，DA的效果比较好；从电压稳定性指标来看，DA的指标值更小，因此说明电压稳定性较好；从目标函数值来看，DA的最优值是最低的，也就是说，综合降低线损和提高电压质量来看，DA的求解的优化方案更具有优势.综上可见，DA在解决配电网无功优化问题中更具优势.

4 结论

从安全性角度出发，以最小化线损、电压偏差和电压稳定性指标值为综合目标，建立了含分布式电源的低压配电网无功优化模型，其中目标函数中各指标的权重系数采用了变异系数法进行客观赋值，提高了模型在特定问题场景中的适应性.采用蜻蜓算法对该无功优化问题进行求解，通过改进的IEEE 33节点系统进行仿真验证，结果表明：所提解决方案可得到全局最优解，在降损节能、提高配电网运行安全性方面有显著效果.