改进HHT 算法在导弹工作模态辨识中的应用*
2022-07-11谢金松薛林高庆丰
谢金松,薛林,高庆丰
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团有限公司 第二研究院,北京 100854)
0 引言
导弹飞行时弹体受到周身分布的复杂激励,会产生弹性振动。横向振动被弹上加表和陀螺仪量测,使回路引入额外输入,严重时会造成导弹失稳,如美国的Lark 和印度ASLV-D2 火箭,因此需对导弹弹性振动进行分析。工程中常通过地面模态试验确定导弹模态,依据模态参数设计凹陷滤波器以抑制振动影响[1-2]。导弹实际飞行工况与地面振动试验环境存在差异:一方面,导弹飞行中噪声源(环境杂波、热噪声等)复杂且激励(气动力与扰流)无法量测;另一方面,导弹弹性频率会随燃料燃烧造成的质量衰减而改变,是典型的时变过程。较之地面振动试验,辨识导弹工作模态更有意义。
利用传统算法辨识导弹工作模态存在缺陷:时域或频域辨识方法都难以对时变模态进行分析;时域辨识对噪声敏感,辨识精度低;频域辨识存在傅里叶变换截断误差,且大都要求激励已知[3]。Hilbert-Huang 变换(HHT)是一种非平稳信号处理技术[4],与传统的数据分析方法相比,HHT 具有分析精度高、自适应性强、物理意义明确、可处理非平稳信号等优势。HHT 存在端点效应和模态混叠2 个固有缺陷,国内外学界为解决此二类问题提出了大量算法。如针对端点效应的镜像延拓方法[5]、ARMA 时间序列线性预测方法[6]、多项式拟合延拓方法[7]、边界波形匹配延拓法[8]等,均可有效抑制端点漂移现象。Huang 等[9]提 出 的 集 合 经 验 模 态 分 解(en⁃semble empirical mode decomposition,EEMD)是抑制模态混叠的经典算法,后人对模态混叠的抑制大都为该算法的改进;Yeh 等[10]提出的互补集合经验模态分解方法(complementary ensemble empirical mode decomposition,CEEMD)有效减少了EEMD 算法中辅助噪声的影响,练继建等[11]将该方法应用到水坝模态识别中;陈永高等[12]参考肖瑛等[13]的思路,认为各阶IMF 的非确定正交性是模态混叠的来源,通过在EEMD 算法中嵌入“解相关算法”和“谱系聚类”方法使各阶IMF 强制正交,对模态混叠加以抑制,并对斜拉桥振动模态进行辨识。
本文提出一种多次自适应加噪的改进HHT 模态辨识方法,以两端自由的变质量欧拉梁作为飞行导弹模型,仿真出飞行状态下的导弹前三阶振动模态,使用改进后的HHT 算法辨识其振动参数。与传统算法相比,改进HHT 方法有效提高了模态筛分精度,更适用于具有时变性的导弹工作模态辨识。
1 HHT 模态辨识方法
HHT 算法包含经验模态分解(empirical mode decomposition,EMD)和希尔伯特变换2 个步骤。经验模态分解是将不同时间尺度的信号分量提取出来,即筛分出振动信号中的各阶固有模态函数(in⁃trinsic mode function,IMF)。EMD 结 束 后,对 各 阶IMF 进行希尔伯特变换,拟合变换后的解析信号即可解算出各阶频率与阻尼比。
利用EMD 筛分振动信号各阶模态的流程如下:
(1)对原始信号x(t)的极大值点和极小值点分别进行3 次样条插值,求出信号上下包络线xmax(t)和xmin(t)。
(2)得到上下包络线xmax(t)和xmin(t)的均值函数m(t) = (xmax(t) +xmin(t))/2。
(3)用原始信号x(t)减去m(t),得到待判别信号h1(t)。
(4)若h1(t)满足IMF 条件,即认为h1(t)为原始信号的一阶IMF,用原始信号减去h1(t)得到的新信号c1(t)作为原始信号,重复以上步骤,直至把所有的IMF 全部找出。
(5)若h1(t)不满足IMF所需条件,用h1(t)作为原始信号重复以上步骤,直至把所有的IMF 全部找出。
Huang 给出的IMF 判定条件为:信号零极点数目相等或差1;信号局部包络线均值为0。此条件使各阶IMF 具有均匀的波动性与对称性,满足各阶振动模态的要求。
筛分完成后,对各阶模态分别进行希尔伯特变换得到其在复域上的解析信号:

式中:P.V.表示柯西主值积分。
各阶模态信号的瞬时幅相函数为
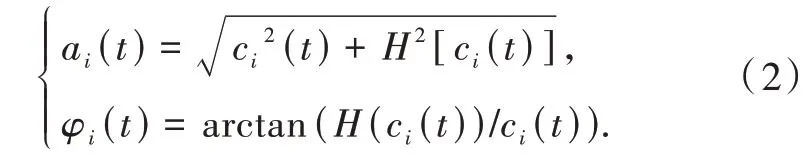
已知单自由度振动表达式为

式中:A为初始振幅;ωdi(t)为第i阶模态有阻尼自振角速度;ωi(t)为该阶模态无阻尼自振角速度;ξi为该阶模态阻尼比。
联立式(2)与式(3),可得各阶振动模态幅相函数的表达式:

利用式(2)求单阶信号的幅相函数后,对幅值函数取对数,得出的曲线斜率即为ξi ωi(t),相位曲线各个时刻的导数为该时刻的有阻尼瞬时频率。二式联立,即可解算出该阶模态的阻尼比ξi与角速度ωi(t)。在导弹飞行过程中,由于质量减小,各阶模态振动频率不断改变,希尔伯特变换提出的瞬时频率的概念可以准确反应模态频率随时间变化的趋势。
2 改进的HHT 模态辨识方法
EMD 存在端点效应和模态混叠2 个缺陷。端点效应是IMF 在信号初末位置的漂移现象,原因为信号的两端点在筛分过程中被视作极点,然而其未必为真实极值,造成极值拟合的包络线在端点处出现漂移。模态混叠现象是EMD 过程难以避免的固有缺陷:由于EMD 算法在数学上无法保证各阶IMF 具有严格正交性,因此筛分出的某阶IMF 中可能包含不同特征尺度的信号。
2.1 极值镜像延拓法抑制端点效应
学界关于端点效应抑制研究已经颇有成果:镜像延拓、极值延拓、数据预测、波形匹配延拓均能有效抑制端点效应。本文通过对信号两端数据的极值点进行镜像延拓消除端点效应的影响。在信号左端,摒弃第一采样点到第一极大值或第一极小值之间的数据,利用第一极大值或极小值作为镜面,对其后5 个极值进行反射,在信号末端做相同处理,构成新的极值信号段。通过极值镜像延拓,可以避免采样初末点参与EMD 过程,消除端点效应。
2.2 集合经验模态分解抑制模态混叠
噪声与高频信号的干扰、各阶模态频率接近都可能造成模态混叠。根据经验,当某模态瞬时频率小于另一模态瞬时频率的2 倍,或者不同阶模态的瞬时角速度与幅度之积不能始终保持Ai ωi≥Aj ωj时便会出现模态混叠现象。
EEMD 算法利用白噪声的零均值性,在原始信号中施加辅助白噪声后再进行EMD,通过多次加噪后加权平均来中和高频噪声和施加噪声的影响,其具体算法流程如图1 所示。
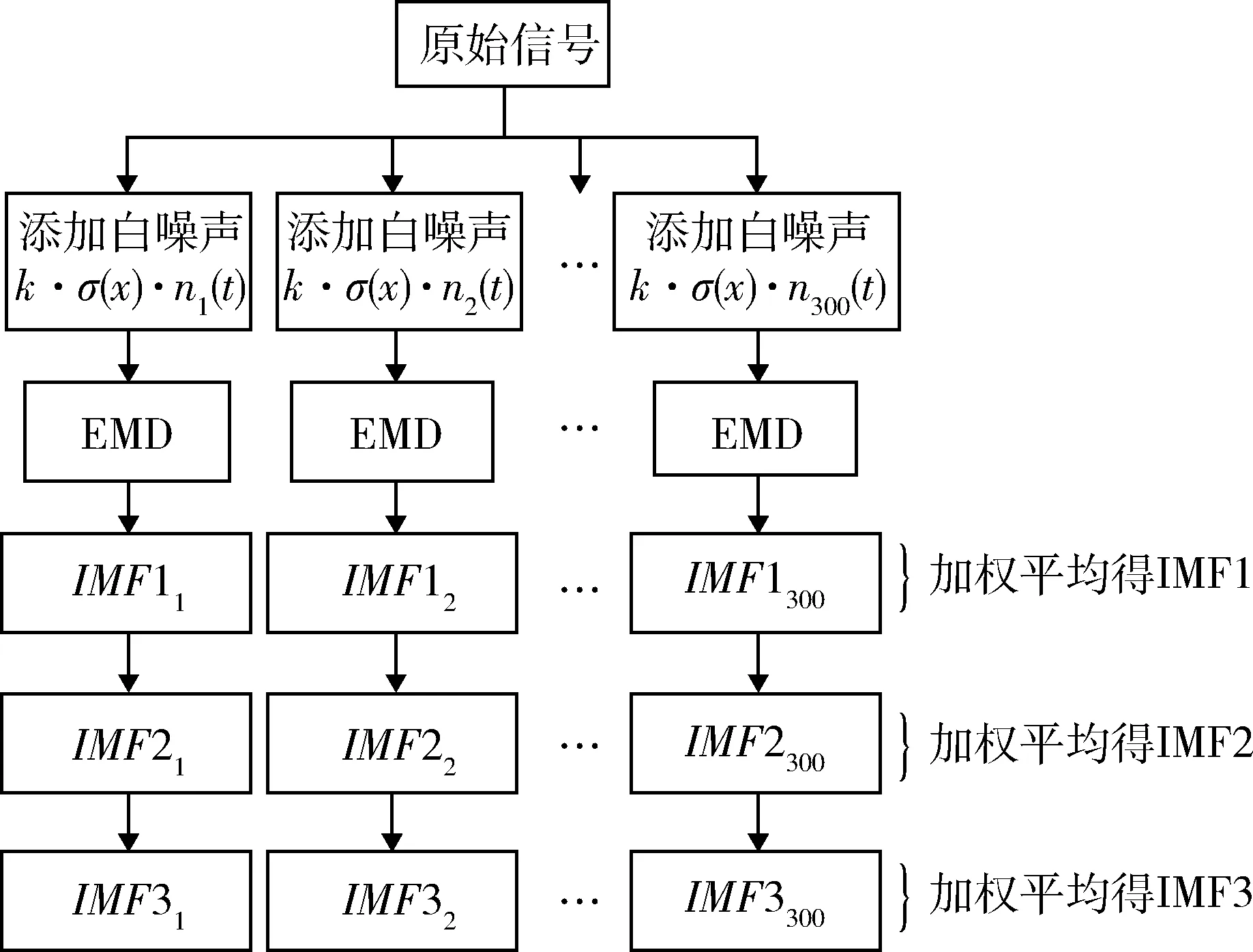
图1 EEMD 算法流程Fig.1 Flowchart of EEMD algorithm
图1 中,ni(t)为辅助白噪声,k为辅助白噪声标准差与原始信号标准差的比值,σ(x)为原始信号标准差。经过实验验证,k取0.2,施加300 次噪声时筛分效果最好,此时辅助噪声对筛分结果的影响小于1%。
2.3 改进的集合经验模态分解方法
通过分析EEMD 分解结果发现,系统对高频IMF 的筛分精度最高,对低频IMF 筛分精度较低;在振动能量较大时段筛分精度较高,在振动能量较小时段筛分精度较低。该现象原因为辅助噪声仅符合高频IMF 功率比特性,且辅助白噪声功率时不变,与逐渐衰减的原始信号功率变化趋势不匹配,故而只对高频高能信号筛分效果好。基于此分析,作者对EEMD 算法提出2 种改进方案:
(1)每次EMD 过程中多次添加辅助噪声:筛分出某阶IMF 后,在残余数据中继续加噪,且该噪声应符合待分解信号的功率比要求。此举可以提高高频高能IMF 之外的各阶IMF 的筛分精度。
(2)为避免随着原始信号衰减,辅助噪声与其功率比逐渐增加,辅助噪声与原始信号应具备相似的功率衰减率。通过实验验证,辅助噪声变为如式(5)形式时筛分效果最好:

式中:|x(1)(t)| 为 归 一化的待分解信 号;k,σ(x),ni(t)与EEMD 算法中取值相同。改进后的算法如图2 所示。

图2 改进的EEMD 算法流程Fig.2 Flowchart of improved EEMD algorithm
3 模态辨识分析
3.1 导弹振动仿真
Euler-Bernoulli 梁两端自由,且忽略其内剪力作用,常用以分析细长体弹性振动问题。本文采用变质量Euler-Bernoulli 梁模拟飞行导弹弹性振动。弹体模型如图3 所示。弹体参数由表1 给出。

表1 导弹弹体参数Table 1 Missile body parameters
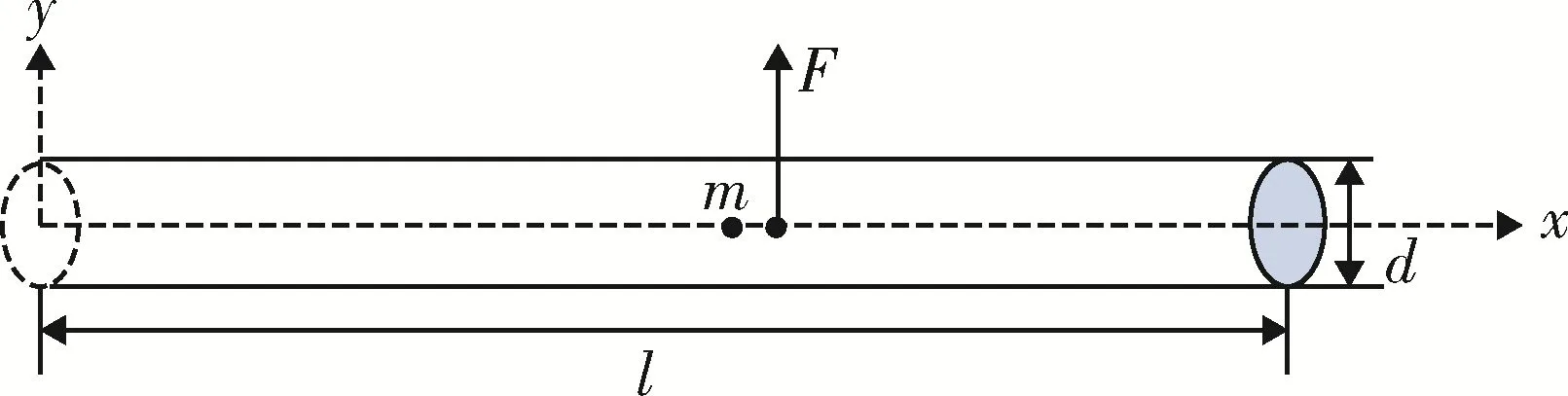
图3 导弹简化欧拉梁模型Fig.3 The missile is simplified to Euler-Bernoulli beam
设导弹前三阶阻尼比ξ1= 0.008 5,ξ2= 0.022 1,ξ3= 0.033 2。在发动机开机的1 s 内,导弹压心位置受到了持续0.3 s 大小1 800 N 的侧向力,由于燃料消耗,导弹体密度以60 kg/m3/s 的速度持续衰减。根据Euler-Bernoulli 梁的固有频率经验公式:

可解得该秒内导弹一阶频率由41.24 Hz 增加至41.96 Hz;二阶频率由114.56 Hz 增加至116.58 Hz;三阶频率由224.54 Hz 增加至228.49 Hz。
已 知Euler-Bernoulli 梁 受 迫振动方 程(7)和Euler-Bernoulli 梁各位置振型方程(8):

联立式(7),(8)可解得各阶模态广义坐标:

根据振型叠加公式可得出弹上加表由于导弹弹性振动测得的相应加速度:
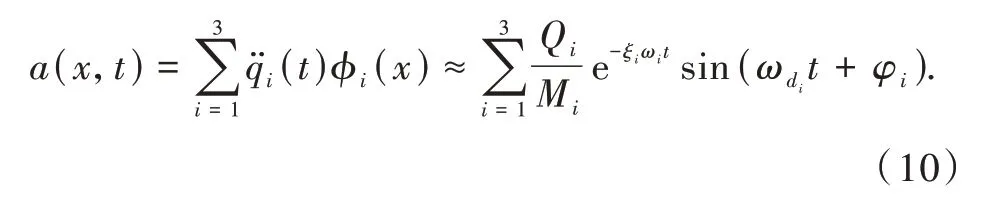
设弹上加表距离弹头距离1 264 mm,量测信号的信噪比为10,该秒内加表量测到的振动信号如图4 所示。

图4 弹上加表量测到的振动信号Fig.4 Vibration signal measured by accelerometer
3.2 各阶模态筛分
利用图4 数据模拟导弹飞行过程中加表量测到的振动信号,截取0.3~0.7 s 内的数据,利用EMD 方法筛分出的各阶IMF 如图5 所示。
由图5 可以看出,EMD 筛分后各阶IMF 左端均出现了端点漂移,各阶IMF在0.35 s前后以及IMF3中0.45 s 前后出现了模态混叠,其原因为各阶IMF 幅值与频率的乘积Ai ωi在这个时间点出现了大小交替。

图5 EMD 算法分解结果Fig.5 Decomposition results of EMD
利用极值镜像延拓方法和EEMD 算法对端点漂移和模态混叠进行抑制,分解结果如图6 所示。
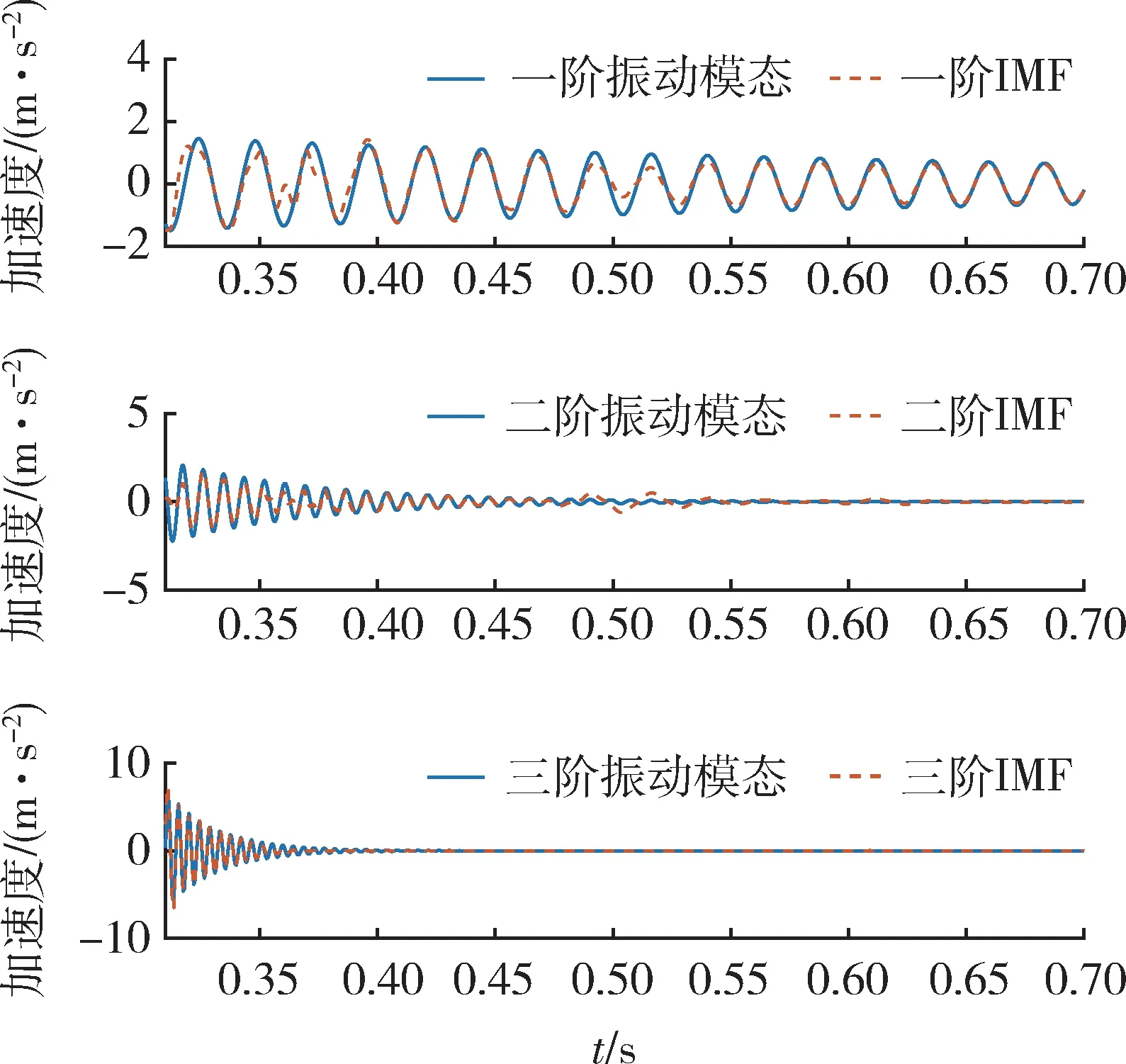
图6 EEMD 算法分解结果Fig.6 Decomposition results of EEMD
由图6 可以看出,极值镜像延拓有效抑制了各阶IMF 左侧的端点效应,EEMD 有效抑制了各阶IMF 中的模态混叠,但IMF2 中0.45 s 之后仍出现了模态混叠。
利用改进后的EEMD 算法进行筛分,分解结果如图7 所示。
由图7 可以看出,对EEMD 进行改进后,IMF2中0.45 s 之后出现的模态混叠也被抑制。

图7 改进EEMD 算法分解结果Fig.7 Decomposition results of improved EEMD
为了定量分析各算法筛分精度,引入参数v作为精度评价指标:
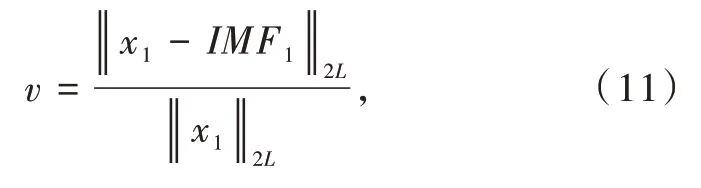
式中:下标2L表示向量的2 范数。
分解精度越高,参数v取值越小。以上3 种算法得出的各阶IMFv值如表2 所示。
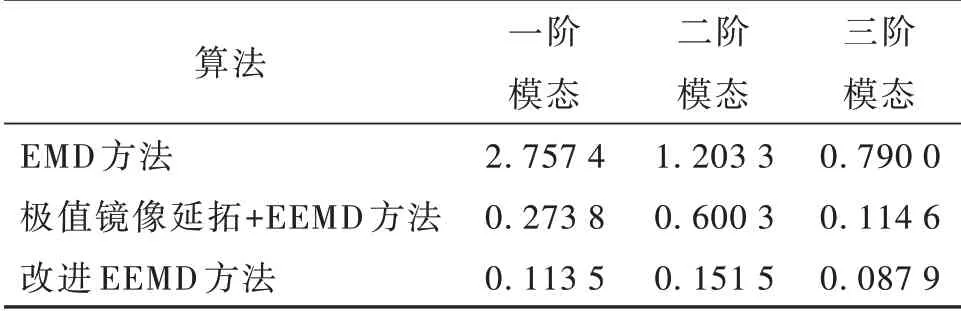
表2 各算法分解精度vTable 2 Decomposition accuracy of each algorithm
结合本节图表仿真结果可知,EMD 几乎无法抑制模态混叠和端点效应,EEMD 虽然提高了辨识精度,但仍无法完全抑制模态混叠,改进后的EEMD 筛分精度最高。
3.3 振动参数辨识
传统工程中常使用峰值对数衰减法进行模态辨识:提取各阶衰减信号的峰值点的对数:
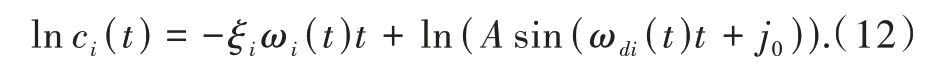
对lnci(t) 进行一阶拟合,求得斜率即为ξi ωi(t),再根据峰值点的时间间隔确定振动角速率ωi(t),从而可以解算出阻尼比ξi。
以IMF1 为例,对其峰值对数拟合结果如图8所示。
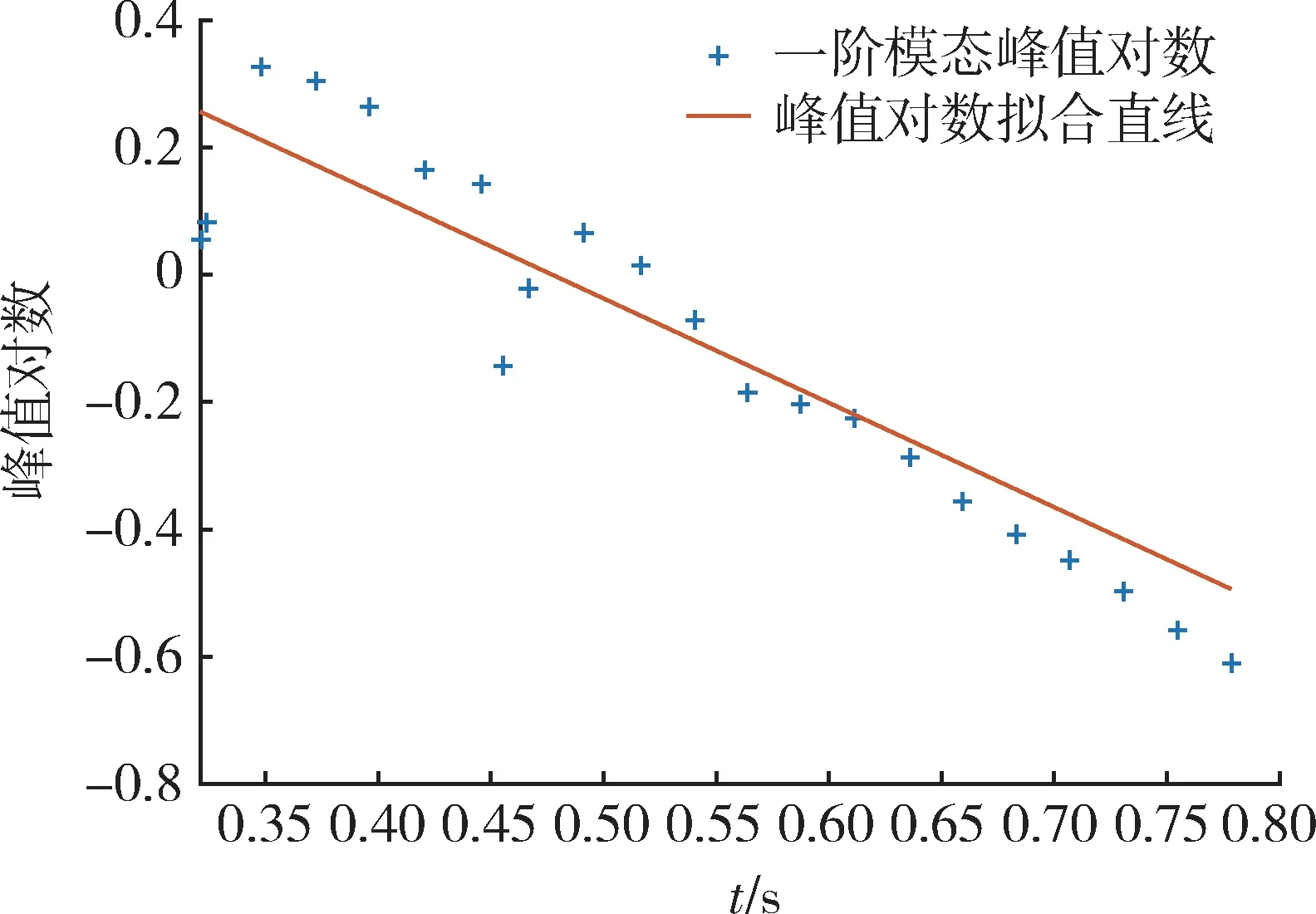
图8 峰值对数衰减法辨识过程Fig.8 Identification process of peak logarithmic attenuation
峰值对数拟合得到的直线斜率ξ1ω1为2.045 8。根据峰值时间差的均值则可得出采样时间内平均周期0.022 5 s,可算出利用该算法辨识出的频率为44.4 Hz,阻尼比为0.007 4。
依据式(4),利用希尔伯特变换得出一阶IMF 幅相函数后,对幅值对数进行拟合,如图9 所示。

图9 一阶IMF 幅值对数变化趋势Fig.9 Variation trend of the logarithm of the first oder IMF amplitude
对相位进行求导,可以得出瞬时频率变化趋势如图10 所示。
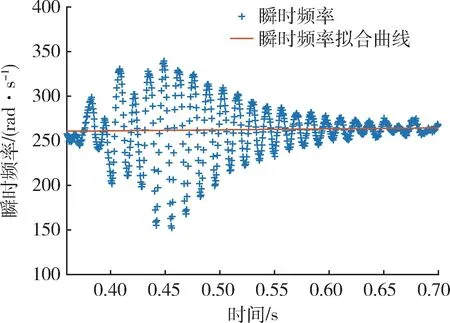
图10 一阶IMF 瞬时频率变化趋势Fig.10 Variation trend of the instantaneous frequency of first oder IMF
对该时段内所有信号幅值对数进行拟合,得到的直线斜率ξ1ω1为2.212 2。由图10 中的拟合直线可以看出,该时段内一阶IMF 瞬时频率有增加的趋势,瞬时频率由260.68 rad/s 增加到了264.51 rad/s,正是这一时段内由于导弹质量衰减造成的频率增加。将瞬时频率均值与ξ1ω1取值进行联立,可得利用该算法辨识出的阻尼比为0.008。
分别利用以上2 种方法对三阶模态参数进行辨识,结果如表3 所示。
希尔伯特辨识用到采样周期内所有数据点,比仅利用的峰值数据的对数衰减法对噪声影响的容错率更高,也避免掉了采样频率不足造成的误差。由于引入瞬时频率的概念,希尔伯特辨识方法可以反应出即导弹的频率的时变性,这是峰值对数衰减法无法做到的。
分析表3 所示结果可知,无论哪种辨识方法,IMF2 与IMF3 的辨识精度不如IMF1,其原因为高频信号频率与采样频率更近,峰值处的采样值与真实极值的偏差更大,且高频信号衰减迅速,衰减至低能后噪声影响增大,故而辨识精度较低。考虑到高频信号衰减迅速且频率高于制导回路带宽,工程中常采用低通滤波方法将其滤去或忽略其影响。
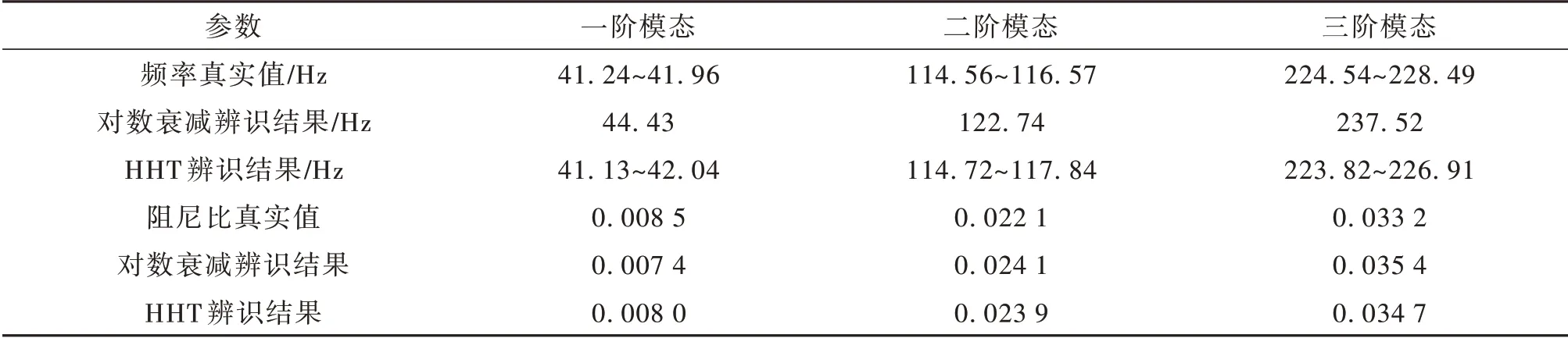
表3 各算法辨识结果Table 3 Identification results of each algorithm
4 结束语
本文对于HHT 方法进行了改进,通过极值镜像延拓方法抑制了模态分解时的端点效应,通过多次施加自适应辅助白噪声的改进EEMD 方法抑制模态混叠,并对导弹振动的仿真信号进行处理,成功辨识出各阶振动频率和阻尼比。
实际飞行之中,考虑到导弹的体密度变化较大,发动机初始点火阶段振动频率约为空弹振频的0.75 倍左右,利用该方法对导弹在不同空域内弹道飞行的加表量测信号进行处理,可以得出导弹振动模态的全弹道变化趋势,为导弹稳定性分析和凹陷滤波器的设计提供更加精确的参考。
