大交会角约束下非线性系统三维能量最优制导律*

2022-07-11祝月徐俊艳王晓东宋勋王蒙一

现代防御技术 2022年3期

祝月，徐俊艳，王晓东，宋勋，王蒙一

（北京电子工程总体研究所，北京 100854）

0 引言

随着各国军事力量和科学技术的不断发展，过去单一飞行器之间的攻防对抗已经不能满足当前的作战需求。在当前信息化作战的背景下，为了提高打击精度和打击效果，多弹协同打击多目标的作战方式开始兴起［1］，并逐渐成为各国的研究热点。

在多弹协同打击多个目标的作战场景中，各导弹的发射时间受拦截弧段的影响不能任意给定，因此需要采用多弹齐射的方案［2］。多弹齐射的制导律设计问题需要考虑诸多约束［3］。首先，为避免前方导弹击中目标时的光电效应对传感器瞬间失灵的影响以及避免碰撞产生的碎片干扰，各导弹间的交会角要形成较大的差异。第二，为保证拦截精度，需要使得脱靶量尽可能小。同时，为保证工程可实现性，还需要使全程的能量消耗尽可能小。

根据国内外学者的相关研究，考虑交会角和脱靶量共同约束的制导方法可以总结为滑模变结构控制法（SMC）、最优控制法，以及剩余时间多项式拟合法（TPG）等三大类［4］。文献［5-6］针对静止和低速目标设计了一种二维滑模制导律，在控制交会角的同时，能够使制导指令在交会前收敛到0。文献［7-8］针对导弹速度为常值及目标静止的情况提出了一种考虑末端脱靶量和交会角约束的二维最优制导律。其中，损失函数用能量代价除以剩余飞行时间的幂指数表示，而后通过求解线性二次型得到制导律的最终表达式。该论文通过计算导弹运动轨迹曲线对剩余飞行时间进行估计，提高了对脱靶量控制的精度。还有学者［9-10］提出将制导指令作为剩余飞行时间的多项式（TPG）的制导方法，通过构造制导指令多项式各项的系数来满足交会角和脱靶量的约束。这种方法简便易行，同时过载的形式简明直观，便于对其进行约束。

通过对国内外现状的比对和分析，可以总结出当前研究存在的几点问题。首先，现有的研究主要集中在导弹速度恒定和目标静止的情况［11-12］。这种情况下制导状态方程的设计和求解相对简单，同时也容易求解出较为精确的剩余飞行时间，其脱靶量和角度偏差都会比较小［13］。然而，在协同打击高速非机动目标这一场景下，不但目标是高速运动的，导弹速度的大小通常也是时变的［14］。解决这种情况下制导律的设计问题对于工程应用十分必要。另外，现有制导律大多是基于二维场景提出的。对于三维制导律，尤其是大交会角约束下制导律的设计和分析存在较大欠缺。

为解决上述问题，本文针对多个导弹协同打击多个高速非机动目标的背景，将多对多制导律设计问题展开成多组一对一基本单元的制导律设计问题，提出了一种适用于弹目高速运动场景下的三维制导律。该制导律可以同时满足脱靶量、交会角和交会时间等多个约束，并且能够降低制导过程的能量代价，具有较强的理论意义和工程价值。

1 问题描述及模型建立

1.1 问题描述及假设

在本文研究的基于协同场景下多对多打击高速非机动目标的场景中，导弹间的信息交换用于提高导弹的抗干扰能力和目标的捕捉概率，而各个导弹制导指令的生成是相对独立的。在打击过程中，母弹升空后在一定的位置释放出子导弹，形成多组多对一或一对一的防御网络。假设导弹的反应时间和状态调整时间忽略不计。认为导弹和目标所受空气阻力忽略不计。在拦截过程中，目标受重力作用做高速非机动运动，导弹受重力和垂直于弹体方向的法向过载共同作用。

1.2 弹目相对运动模型

三维空间内的拦截几何如图1 所示。

图1 三维空间内弹目拦截几何Fig.1 Three-dimensional dynamics of missile and target

OXIYIZI是以发射点为原点的惯性坐标系。r和q分别是弹目相对距离和视线角。vM，θM，ψvM以及vT，θT，ψvT分别是弹目速度、弹道倾角和弹道偏角。导弹和目标都受重力加速度g的作用，此外，导弹还受发动机施加的法向过载的作用。该过载在弹道坐标系中垂直于速度方向的的投影为amny和amnz。则导弹和目标在三维弹道坐标系实际的法向加速度amy，amz，aty，atz可表示为

导弹和目标的速度及弹目相对距离在三维发射点惯性坐标系内的投影vmx，vmy，vmz，vtx，vty，vtz，rx，ry，rz可以表示为

将三维空间分解成铅垂和水平2 个二维平面，通过分析2 个平面内的运动，建立2 个平面相互耦合的状态方程［9］。2 个平面内的弹目相对运动几何分别如图2~3 所示。图中，vmxy，vtxy，rxy，vmxz，vtxz，rxz分别是vM，vT，r在OEXIYI平面和OEXIZI平面上的投影。

图2 铅垂面弹目拦截几何Fig.2 Dynamics on vertical plane

则导弹与目标机动的动力学方程为

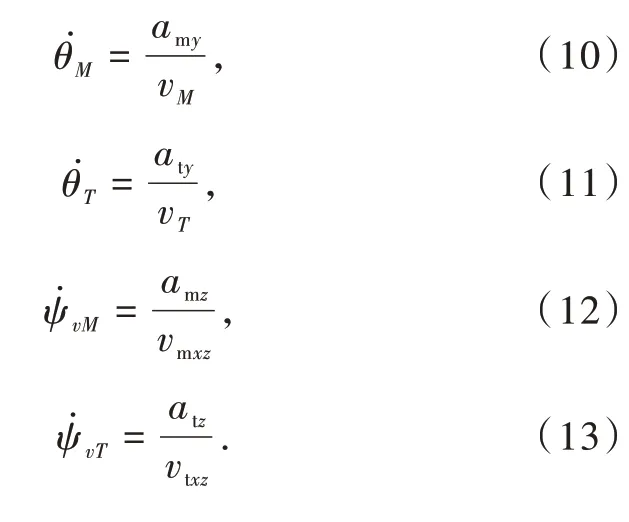
图3 水平面弹目拦截几何Fig.3 Dynamics on horizontal plane

1.3 制导模型

1.3.1 解耦模型的问题

传统的运动学模型通常将水平面和铅垂面解耦考虑［15］。即，在考虑一个平面内的运动时，认为另一个平面内的弹道角瞬时不变，并且导数为0。此时amy和amz可以分别由OEXIYI和OEXIZI内的制导律生成。OEXIZI平面内，的表达式为

可以发现，在式（14）~（15）的求导过程中没有考虑和项，即认为θM和θT是瞬时不变的。

OEXIYI平面同理。

在本文研究的多个导弹协同打击高速运动的目标场景下，为保证拦截精度，部分导弹的交会角可能会非常大。在这种情况下，临近交会前弹道角的变化速率很大，会导致较大的脱靶量和角度偏差。因此，解耦模型在大交会角情况下并不适用。

1.3.2 三维耦合制导模型

针对解耦模型的问题，本节提出了一种将铅垂面和水平面耦合考虑的三维制导模型。选取系统的状态变量为

可以得到系统的状态空间表达式为

2 制导律设计

本小节将以三维耦合制导模型为基础，设计一种考虑交会角和脱靶量共同约束的三维能量最优制导律。三维能量最优制导律的损失函数如下：

式中：amy，amz为三维弹道坐标系中导弹实际的法向加速度，可以得到哈密尔顿函数为

代入状态方程并对控制变量求偏导，得到系统的控制方程：

系统的终端状态x1(tf)，x3(tf)，x4(tf)和x6(tf)固定，x2(tf)，x4(tf)自由。这是一个终端状态部分固定系统的制导律设计问题。系统的协态方程为

求解协态变量，可得：

其中，k1，k3，k5，k6为待求参数。可以得到过载的最终形式：

其中，tgo=tf-t表示剩余飞行时间，需要根据当前时刻的弹目相对距离r和视线方向的相对速度ṙ估计：

只要求解出系统的终端状态k1，k3，k5，k6，便可以得到系统的控制输入。接下来将利用系统的终端状态x1(tf)，x3(tf)，x4(tf)和x6(tf)来求解这2 个未知参数。系统的终端状态可以表示成：

其中，

Φ(tf，t)为系统的状态转移矩阵。采用欧拉积分，可以将式（41）化简为

利用伪逆函数pinv，可以求出未知参数K：

代入式（39），即可得到导弹在弹道系下实际法向加速度amy，amz的数值解。根据式（1），（2）可以得到弹道系下垂直于速度方向的控制指令amny，amnz。通过坐标变换，将amny，amnz转换到弹体坐标系，得到实际的过载指令。amny，amnz到弹体坐标系下过载amyq，amzq的转换关系为

式中：av项是垂直于弹体方向的过载在导弹速度方向上的分量。据此解出：

考虑av影响后的速度变化率为

3 仿真校验

本节将通过仿真分析，验证制导律对脱靶量和交会角偏差控制的有效性。OEXIYI和OEXIZI平面上的零控脱靶量表达式为

能量消耗定义为

导弹在重力加速度下飞行，且受垂直于弹体方向的法向过载控制。目标仅在重力加速度作用下飞行。模型解算周期为0.001 s，制导周期0.02 s。末端期望交会倾角和交会偏角范围取-35°~35°。制导的初始条件见表1。图4~6 为三维弹目运动轨迹和弹体系下的法向过载。

图4 弹目三维运动轨迹Fig.4 Three-dimensional trajectories of missile and target

表1 选择的初始值Table 1 Initial values

图5 弹体系y 轴方向需用过载Fig.5 Normal load on y axis

表2 记录了终端脱靶量、交会角偏差及总能量消耗。终端脱靶量的绝对值的范围为0.000 013 m到0.234 181 m，交会角偏差的范围为0.000 01°~0.000 22°，满足攻击时对脱靶量和交会角精度的要求。

表2 命中时刻状态值Table 2 Values at impact time

图6 弹体系Z 轴方向需用过载Fig.6 Normal Load on Z axis

接下来将对本文提出的耦合模型与解耦模型［9］进行对比和分析，以证明在大交会角情况下，耦合模型在脱靶量、交会角控制偏差和能量代价上的优越性。

基于文献［9］建立的解耦模型，通过建立和求解最优控制的协态方程和横截条件便可以得到amy和amz的最终表达式。，OEXIYI和OEXIZI平面上的损失函数可以分别表示为

选用表1 的初始值，设定模型解算周期0.001 s，制导周期0.02 s。末端期望交会倾角和交会偏角范围取-35°~35°。得到解耦模型的终端脱靶量和交会角偏差，并将耦合模型的终端脱靶量和交会角偏差作为对比，记录在表3 中。

表3 中的数据表明，在相同的交会倾角和交会偏角下，耦合模型的能量代价要明显优于解耦模型，并且终端脱靶量和交会角偏差更小。当期望的交会倾角和交会偏角增大时，解耦模型的终端脱靶量和交会角偏差也会随之增大。这个结果表明，在末端存在交会角约束，尤其是期望的值较大时，按照耦合模型推导的制导律要明显优于解耦模型。