Al/PTFE 活性材料冲击载荷作用下响应特性研究*

任耶平，刘 睿，陈鹏万，郭岩松，胡启文，葛 超，王海福

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

活性材料是一种或多种金属以一定的工艺制备而成的先进复合材料。这类材料具有常态惰性钝感、冲击载荷作用下发生化学反应并释放能量的特点，被广泛应用于含能破片、聚能药型罩等新型毁伤元。活性材料在冲击载荷下的反应行为涉及复杂的力-热-化耦合响应过程，研究其冲击响应特性是该领域的热点方向。

近年来，铝（Al）/聚四氟乙烯（polytetrafluoroethylene, PTFE）作为典型的活性材料受到了广泛的关注。在材料制备方面，以压制和烧结等方式为主的粉末冶金技术被用于制备具有反应活性的Al/PTFE 块体材料。Joshi较早地提出了以模压烧结的工艺制备Al/PTFE 活性材料。在此基础上，阳世清等获得了不同制备工艺条件下Al/PTFE 活性材料的理化性能和力学性能，确定了最优的制备工艺条件。Nielson 等提出了用湿法工艺代替干法工艺，可以使材料混合更加均匀。于钟深等采用冷等静压和真空烧结工艺制备了含 TiH的Al/PTFE 活性材料，通过准静态压缩实验测试了材料的力学性能。目前，获得致密的Al/PTFE 块体材料制备工艺已较为成熟。

针对Al/PTFE 材料的动态力学行为、点火及释能行为，已开展了大量的研究工作。通常采用分离式霍普金森压杆（split Hopkinson pressure bar, SHPB）系统，研究Al/PTFE 材料的动态力学行为。研究结果表明，Al/PTFE 材料具有应变率效应，动态屈服强度小于50 MPa，明显低于传统金属材料。通过添加高密度材料如钨，能够提升材料的屈服强度，但其屈服强度的提升并不显著。Al/PTFE 材料在动态加载条件下能够发生点火反应。Ge 等通过SHPB 动态加载，结合高速摄影以及应变测量，得到了Al/PTFE 活性材料的点火反应应变率阈值和应力阈值，并证明了材料变形破坏是诱导点火的重要因素。Ren 等设计了不同初始缺陷的Al/PTFE 样品，研究了缺陷对活性材料点火行为的影响规律。研究结果表明，随着初始缺陷的增加，点火阈值明显降低。在Al/PTFE 材料释能方面，Wang 等、Zhang 等和Xiong 等采用经典的Ames 撞击实验装置，研究了Al/PTFE 材料的撞击释能行为，通过压力传感器和高速摄影分别记录释能产生的超压和剧烈程度，评估了反应释能效率。王海福等提出了一种测量活性破片释能水平的方法，建立了活性材料能量释放率和碰撞速度的关系。上述研究给出了Al/PTFE 材料在动态加载下的反应特征，但对Al/PTFE 材料在动态加载条件下的化学反应过程讨论较少。

爆炸加载被应用于研究活性材料在极端加载条件下的响应行为。Li 等采用爆炸冲击直接起爆PTFE/Ti/W 活性材料，观测冲击波传播过程中的化学反应，发现了该化学反应具有不可自持的特征。Lee 等对Mn/S 活性材料进行了爆炸加载实验，没有直接观测到反应自持现象。Gur'ev 等对Zn/S 材料采用相同的爆炸加载实验，观察到了冲击波速度随着传播距离的延长出现先迅速降低、后缓慢上升至稳定的现象，证明了该体系在爆炸加载条件下具有固相爆轰行为。Dolgoborodov 等通过采用机械活化方法处理Al/PTFE 混合粉末，制备了密度为0.4～0.5 g/cm的疏松试样，对其进行爆炸加载实验，同样观察到了固相爆轰现象，其爆速为700～1300 m/s。由此可见，活性材料在爆炸加载条件下是否具有自持反应行为仍存在争议，且自持反应条件并不清楚。但是，活性材料化学反应释能过程对爆炸载荷作用下材料的状态具有显著的影响。

综上所述，本文中拟针对Al/PTFE 活性材料在冲击载荷下的响应行为，制备密度为1.92 g/cm、具有反应活性的Al/PTFE 材料，采用拉氏实验分析方法，利用锰铜压阻计观测冲击波在传播过程中的演化，基于AUTODYN 有限元程序，开展拉氏实验数值模拟，运用Lee-Tarver 三项式点火反应模型，对冲击加载下Al/PTFE 活性材料的响应特征进行分析。

1 拉氏实验

1.1 样品制备

选取粒径为10 µm 的Al 粉和粒径为15 µm 的PTFE 粉，制备Al/PTFE 块体材料。Al 粉和PTFE 粉纯度分别为99.5%和99.9%。考虑Al 和PTFE 的化学反应配比，Al 和PTFE 的质量分数分别为26.5%和73.5%，保证Al/PTFE 块体材料具备最优的反应放热能力。

为了制备Al/PTFE 块体材料，将指定比例的Al 粉和PTFE 粉放入无水乙醇中，利用磁力搅拌机进行充分的机械混合，直至Al 粉和PTFE 粉均匀分散在无水乙醇中。通过干燥处理，形成Al 和PTFE 混合粉末。由于Al 和PTFE 混合粉末具有一定黏性，干燥过程容易产生结块现象，通过筛选剔除结块部分，最后获得均匀的Al/PTFE 混合粉末。图1(a)为筛选后的样品粉末扫描电镜（scanning electron microscope,SEM）图像，显示了粉末细观组织结构，图1(b)～(d)为元素能谱（elemental energy spectrum, EDS）分析图，分别给出了Al 元素、F 元素和C 元素的分布情况。结果表明，球形Al 颗粒较均匀地分散在絮状的PTFE 中。

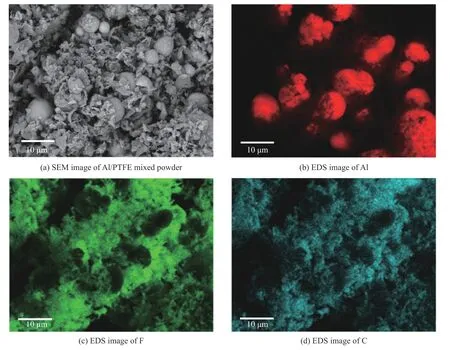
图1 Al/PTFE 混合粉末SEM 图像和组分EDS 图像Fig. 1 SEM image and composition EDS images of the Al/PTFE mixed powder

另外，对Al/PTFE 混合粉末进行了X 射线衍射（X-ray diffraction, XRD）分析，结果如图2 所示，未发现Al 和PTFE 的反应产物，证明材料在制备过程中混合粉末没有发生反应，确保所制备的块体材料具有良好的反应活性。

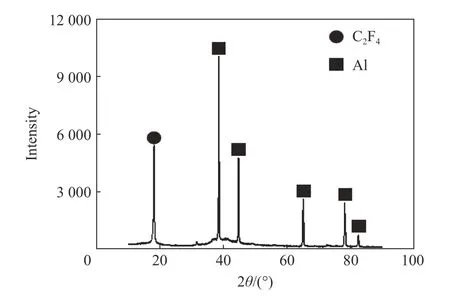
图2 Al/PTFE 混合粉末XRD 分析结果Fig. 2 XRD analysis result of the Al/PTFE mixed powder

进一步通过冷压成型技术获得尺寸为 ∅ 50 mm×3 mm 的Al/PTFE 圆片块体，即将Al/PTFE 粉末放入模具内，利用压机对其进行压制。首先，压力以10 MPa/min 的速率升高到10 MPa，并维持压力3 min；然后，以10 MPa/min 的速率进行压力卸载，如图3 所示。图4 为Al/PTFE 圆片块体实物图，其密度为1.92 g/cm，孔隙率为17%。

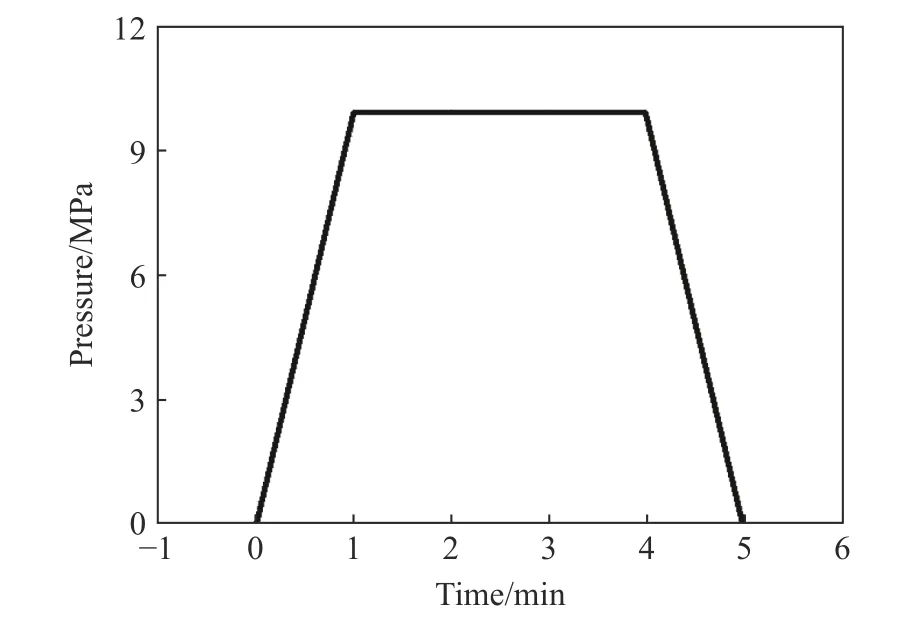
图3 Al/PTFE 冷压成型压力-时间曲线Fig. 3 Pressure-time curve of Al/PTFE cold-pressed formation

图4 尺寸为∅ 50 mm × 3 mm 的Al/PTFE 圆片块体Fig. 4 Al/PTFE round flakes with the size of∅ 50 mm × 3 mm

1.2 实验装置

拉氏实验已被广泛用于研究炸药冲击起爆特性研究，近年来，也被用于活性材料的冲击波传播特性的研究。图5 为给出了拉氏实验装置。整个实验装置主要由主发药、铝隔板、Al/PTFE 圆片块体材料、锰铜压阻计、恒流源以及示波器组成。通过主装药爆炸加载方式，冲击波经过铝隔板衰减进入Al/PTFE 材料。每块样品上表面中心位置安装锰铜压阻计测量冲击波传播路径上的变化过程。通过调节铝隔板厚度，达到控制入射冲击波强度的目的，获得不同输入压力条件下Al/PTFE 样品反应对冲击波传播的影响。其中，主装药选用PBX-8701，其尺寸为 ∅ 50 mm×15 mm。铝隔板厚度分别为5 和10 mm。试样是由4 片尺寸为 ∅ 50 mm×3 mm 的Al/PTFE圆片块体材料组成。

图5 拉氏实验装置Fig. 5 The Lagrangian experimental setup

使用的锰铜压阻计如图6 所示，尺寸为65 mm×15 mm×0.06 mm，传感器前端敏感区域位于试样中心位置，在冲击波载荷作用下电阻发生变化，导致在恒流条件下电压发生变化。冲击波压力为：

图6 锰铜压阻计Fig. 6 Manganese copper pressure sensors

式中：为冲击波压力，∆为锰铜压阻计受到冲击后的电阻变化，为锰铜压阻计的初始电阻。

2 实验结果

2.1 冲击波压力的演化

图7 为在铝隔板厚度为10 和5 mm 的条件下，冲击波在Al/PTFE 材料中传播过程中压力的变化，图中为传感器到铝隔板底面的距离。重点关注不同位置的冲击波峰值压力演化过程，峰值压力代表了冲击加载过程中的典型特征量，其演化过程取决于材料物理属性和化学反应特性。当铝隔板厚度为10 mm 时，冲击波在=0 mm 处的压力为8.16 GPa。随着冲击波传播，压力幅值不断衰减。当冲击波传播到=9 mm 处时，压力降低为3.46 GPa。当铝隔板厚度为5 mm 时，冲击波在=0 mm 处的压力提高至11.76 GPa。尽管入射压力提高，但是，随着冲击波传播，压力幅值仍然不断衰减。当冲击波传播到=9 mm 处时，压力降低为3.37 GPa。尽管2 种铝隔板厚度条件下冲击波初始压力相差近3.6 GPa，但随着冲击波传播距离增大，冲击波传播到=9 mm 处时，冲击波压力相近。冲击波在活性材料中传播过程，其压力呈现指数衰减，但由于冲击波初始压力相差不大，因此，在经过9 mm 的传播，冲击波压力将衰减到相当水平。

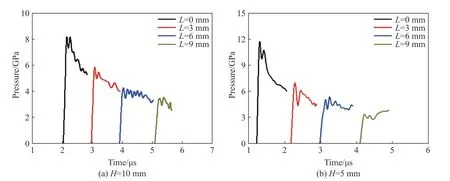
图7 在不同铝隔板厚度条件下，冲击波在Al/PTFE 材料中传播过程中的压力变化Fig. 7 Shock wave pressure changes during shock wave propagation in Al/PTFE materials in the cases of different aluminum partition thicknesses

2.2 冲击波速度的演化

冲击波在材料中的传播速度能够反映材料冲击响应的特征。图8 为不同铝隔板厚度条件下的冲击波传播时间-位移曲线和速度-位移曲线，图中冲击波速度是根据时间-位移曲线确定的，压力增长起跳点作为冲击波到达拉氏位置的时刻。当铝隔板厚度为10 mm 时，冲击波速度从3108 m/s 升高到3184 m/s，随后明显下降至2457 m/s。在冲击波传播至=6 mm 位置时，冲击波速度升高不明显，仅约2.4%。冲击波传播至=9 mm 位置时，冲击波速度衰减明显，约22.8%。当铝隔板厚度为5 mm 时，冲击波速度同样呈现先升高、后降低的趋势：在冲击波传播至=6 mm 位置时，冲击波速度从3144 m/s 升高到3774 m/s，升高明显，约20%；当冲击波传播至=9 mm 位置时，冲击波传播速度降低至2680 m/s，衰减明显，约29%。

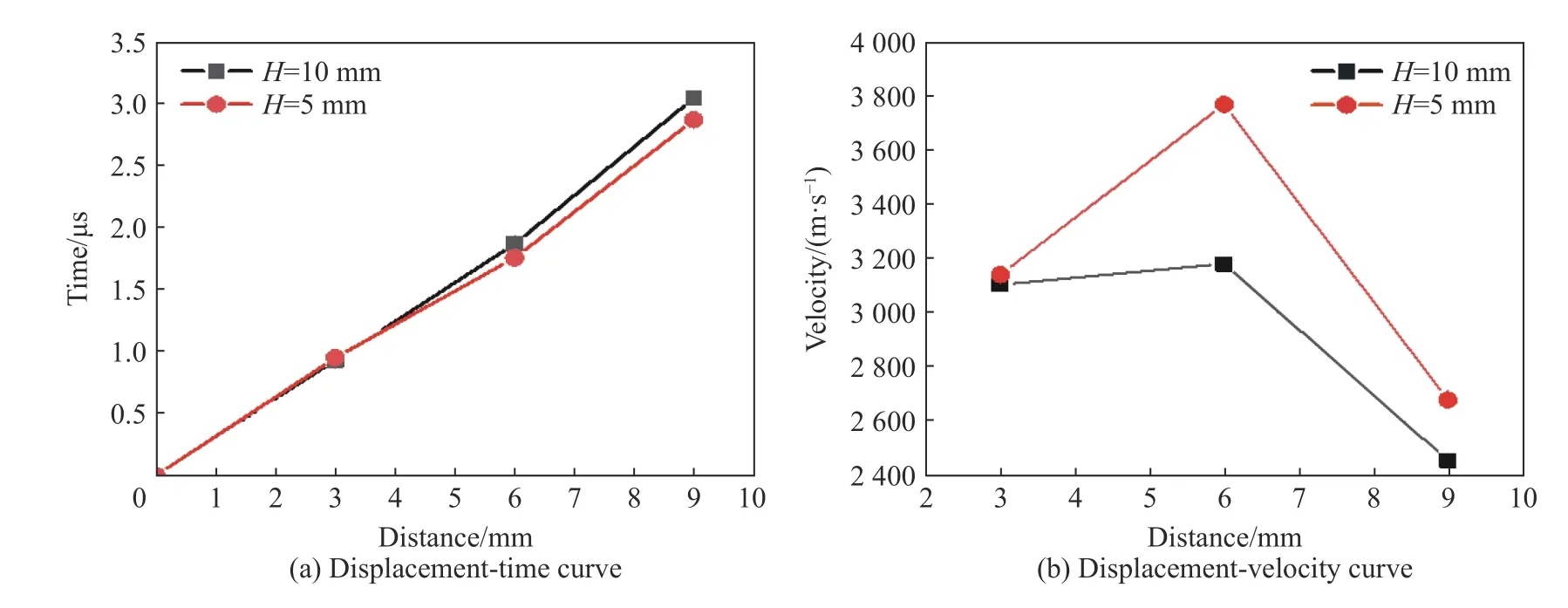
图8 铝隔板厚度分别为10 和5 mm 时的时间-位移曲线和速度-位移曲线Fig. 8 Time-displacement curves and velocity-displacement curves when the aluminum partition thicknesses are 10 and 5 mm, respectively

爆炸冲击波在惰性介质中传播时，由于受到波后和边侧的稀疏作用以及波阵面熵增、材料黏性阻尼损耗等因素的影响，压力和速度随着传播距离的增大呈现指数衰减。但是，图8 中冲击波速度随传播距离的变化曲线并未呈现明显的衰减，这是由于Al/PTFE 样品在冲击加载条件下发生化学反应，能量释放改变了冲击波波阵面后流体状态，有利于加速冲击波传播。但是，随着冲击波传播距离增大，压力幅值在不断衰减，这使受压力控制的Al/PTFE 样品的化学反应速率在不断减弱，导致无法对冲击波实现持续加速。值得一提的是，相比于铝隔板厚度为10 mm 的条件，铝隔板厚度为5 mm 时，加载冲击波的压力和速度更高。因此，Al/PTFE 样品内冲击波速度出现了明显提升。

3 数值模拟

为了进一步研究在冲击波加载条件下化学反应对冲击波传播的影响，通过AUTODYN 有限元数值软件，模拟拉氏实验条件下Al/PTFE 冲击作用下的响应特性。图9 为拉氏实验计算模型，图中1～4 为测点。根据拉氏实验装置真实构型，计算模型选用二维轴对称模型，起爆方式为中心点起爆，材料侧向边界条件设置为自由边界条件，其尾端设置为无反射边界条件，网格类型为拉格朗日网格，网格特征尺寸为0.5 mm。

图9 拉氏实验计算模型Fig. 9 The calculation model for the Lagrangian experiment

其中，主发药PBX-8701 选用Jones-Wilkins-Lee (JWL)状态方程。铝隔板选用Johnson-Cook 模型，引用AUTODYN 软件自带材料库。Al/PTFE 活性材料选用Lee-Tarver 三项式点火反应模型和JWL 产物状态方程，模拟其在冲击载荷作用下的响应特征。

JWL 状态方程为：

式中：为爆轰产物压力；η ，= ρ/为ρ 材ρ料 ρ密度， 0 为材料 初始密度； A、B、R1、R2 和ω 为材料反应常数。各参数数值见表1。

表1 JWL 状态方程参数[29-30]Table 1 JWL-equation-of-state parameters[29-30]

Johnson-Cook 材料模型为：

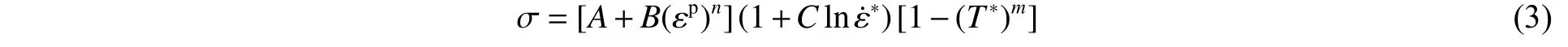
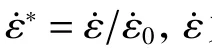
表2 Al 隔板材料 Johnson-Cook 模型参数Table 2 The Johnson-Cook-model parameters of the aluminum partition

Lee-Tarver 三项式点火反应模型为：

式中：等号右边的3 项分别描述材料热点形成过程、慢速反应过程以及快速反应过程；为材料反应度，即材料发生反应的比例；为时间，ρ为 材料密度，ρ为材料初始密度，、、、、、、、、、、和为材料反应常数。由于Al/PTFE 材料自持反应速率较低，快速反应过程对冲击波压力的影响较小，进而反应模型中=0。各参数数值见表3。

表3 Al/PTFE 材料Lee-Tarver 点火增长模型参数[30]Table 3 Lee-Tarver ignition-and-growth model parameters for Al/PTFE materials[30]

拉氏实验计算模型中，设置了4 个观测点用于记录该观测点物理量演变情况，其位置与拉氏实验中锰铜压阻计的放置位置一致。值得说明的是，对于Al/PTFE 而言，虽然冲击条件下其反应速率低于常见的炸药，且并没有像炸药一样爆炸产生大量气体，但是，Jiang 等提出了Al/PTFE 活性材料反应后的产物状态方程仍然可用JWL 状态方程，计算结果与实验结果吻合较好。郭俊通过Lee-Tarver 模型描述Al/PTFE 活性材料的冲击反应过程，并结合实验数据修正了Lee-Tarver 模型，其中用JWL 状态方程描述Al/PTFE 活性材料的反应产物，并通过实验验证了材料参数的有效性。

以隔板厚度为5 mm 的拉氏实验数据为基础，在Al/PTFE 的Lee-Tarver 三项式点火反应模型参数的基础上对式(4)第1 项中的参数和第2 项中的参数进行调整，使4 个观测点的压力历史曲线计算值与对应实验中锰铜压阻计压力历史曲线一致（见图10(a))。其中，参数控制了点火热点形成数量，参数控制了点火后热点迅速扩散慢速反应过程。采用标定的反应模型，对10 mm 隔板厚度下的拉氏实验进行模拟，与对应的压力历史曲线实验结果进行比对，发现10 mm 隔板厚度条件下实验和模拟获得的压力时间曲线吻合较好。因此，这组反应速率方程参数能够较好地描述Al/PTFE 样品材料的反应过程。图10(b)给出了压力演化过程的计算结果和实验结果，验证了Lee-Tarver 模型参数的有效性。实验和模拟的压力时间曲线存在一定差异，即压力起跳时间计算值比实验值略微偏小。这是由于，实验过程中，锰铜压阻计的存在使Al/PTFE 块体材料之间存在一定缝隙，进而导致冲击波传播过程受到一定的弱化。但是，对于计算模型而言，4 片堆叠而成的Al/PTFE 块体材料是连续整体，即块体之间并无缝隙。因此，认为表3 中Al/PTFE 材料三项式点火增长模型参数可用于该类材料冲击反应过程的模拟。

图10 在10 和5 mm 隔板厚度条件下冲击波压力的计算值与实验值Fig. 10 Simulated and experimental results of shock pressure with the partition of 10 and 5 mm in thickness

为了进一步理解冲击波在Al/PTFE 材料中传播行为，设计了 ∅ 50 mm×500 mm 的试样。图11 为 ∅ 50 mm×500 mm 试样的拉氏实验计算模型。该模型仍然为二维轴对称模型，起爆方式为中心点起爆，材料侧向边界条件设置为自由边界条件，其尾端设置为无反射边界条件，网格类型为拉格朗日网格，网格特征尺寸为0.5 mm。计算模型由主发药、铝隔板和Al/PTFE 试样组成。分别选取2 种规格的铝隔板厚度：2 和10 mm。样品中沿轴向设置10 个观测点，间距为50 mm。

图11 拉氏实验500 mm 长样品计算模型Fig. 11 The calculation model of the Lagrangian experiment for the specimen of 500 mm in length

图12 为铝隔板厚度为2 和10 mm 时的压力-时间曲线。计算结果表明，当铝隔板厚度为10 mm，冲击波传播至250 mm 距离时，冲击波峰值压力不断衰减，从8.40 GPa 降低至1.39 GPa；冲击波传播至300～450 mm 时，冲击波峰值压力稳定在1.30 GPa。当铝隔板厚度为2 mm，冲击波传播至250 mm 距离时，冲击波峰值压力不断衰减，从18.00 GPa 降低至1.42 GPa，冲击波传播至300～450 mm 时，冲击波峰值压力稳定在1.30 GPa。冲击波传播达到300 mm 位置时，冲击波峰值压力达到稳定，并未呈现继续衰减的趋势。相比于炸药冲击反应而言，Al/PTFE 材料化学反应释能能力较弱，在强冲击波加载条件下，冲击波并未呈现增长现象，而是在冲击波传播初期呈现随距离衰减的现象，这主要是由材料属性决定的。侧向稀疏波对冲击波压力的衰减作用主要发生在峰值压力之后的演化过程。相比于惰性材料而言，Al/PTFE 材料冲击波峰值压力在一定距离后趋于稳定，并不会随距离不断衰减。另外，炸药爆炸产物膨胀产生的追赶稀疏波有可能追赶上冲击波，并对其产生衰减作用。但化学反应能量释放对冲击波能量衰减进行补偿，维持冲击波的传播，阻碍了冲击波峰值压力的不断衰减。这是在Al/PTFE 这类活性材料中，含化学反应冲击波传播行为的典型特征。

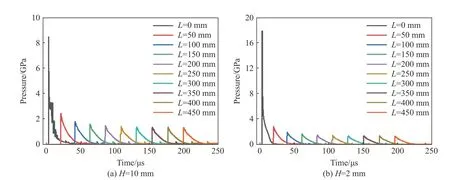
图12 不同铝隔板厚度时压力时间曲线Fig. 12 Pressure-time curves with different aluminum partition thicknesses

对冲击波在2 种铝隔板厚度条件下的传播速度进行了分析。图13 为铝隔板厚度为10 和2 mm 的条件下冲击波速度的变化曲线。计算结果表明，冲击波传播速度随距离增加不断降低，并最终稳定在2180 m/s。冲击波传播经过300 mm 后波速基本保持稳定，该结论与图12 中给出的冲击波压力随时间变化的传播规律一致。冲击波稳定波速远高于Al/PTFE 材料弹性波速1450 m/s。这也是由于活性材料反应释能对冲击波传播具有影响造成的。该现象与Dolgoborodov 等的实验研究结果一致，Dolgoborodov 等采用高氯酸铵为引发药、有机玻璃作为隔板，通过爆炸冲击加载低孔隙率的Al/PTFE活性材料试样，也观测了到稳定的传爆过程。

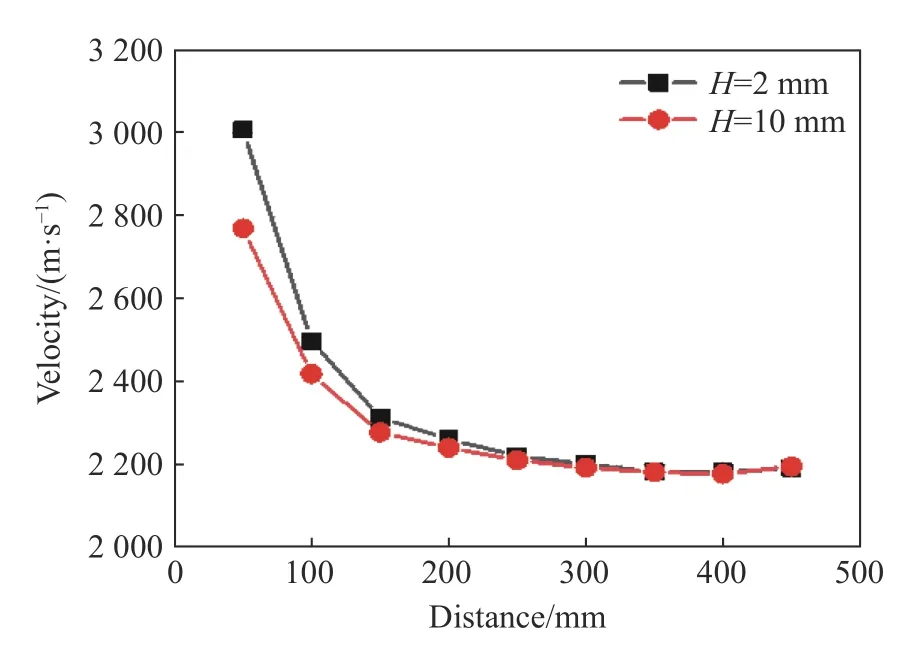
图13 隔板厚度分别为10 和2 mm 时冲击波速度随传播距离的变化曲线Fig. 13 Change of the shock wave velocity with propagation distance when the partition thicknesses are 10 and 2 mm,respectively

进一步对各观测点反应度的演化过程进行了分析。图14 为铝隔板厚度为10 和2 mm 时反应度-时间曲线。两种情况下，反应度均随着冲击波传播距离的增加而不断降低。当冲击波传播到450 mm 位置时，该位置Al/PTFE 材料的反应度降低至约0.17。根据Lee-Tarver 三项式点火反应模型（式(4)）可知，Al/PTFE 材料的反应度由冲击波压力控制。材料反应释能对冲击波的传播具有增强效果。但是，相比于传统高能炸药而言，Al 和PTFE 的反应速率较低，且反应产物没有大量气体生成，这导致对冲击波的增强效果不明显。进而，在冲击波传播经过前250 mm 距离过程中，冲击波幅值不断降低并持续传播。考虑Al/PTFE 材料自身强度远低于冲击波稳定传播压力幅值1.30 GPa，这证明了稳定传播冲击波并不是弹性波，且正是材料化学反应维持了该冲击波的稳定传播。值得说明的是，相比于铝隔板厚度为10 mm 的情况，当铝隔板厚度为2 mm 时，第1 个观测点的反应度略高，约为0.48。这是因为隔板厚度为2 mm 条件下的冲击波入射压力比隔板厚度为10 mm 条件下的约高10.00 GPa，根据Lee-Tarver 三项式点火反应模型（式(4)），Al/PTFE 材料的反应速率随着冲击波加载压力的提高而升高，因此，相应反应度也会随冲击波加载压力的提高而增大。

图14 不同铝隔板厚度时反应度时间曲线Fig. 14 Reaction degree-time curves with different aluminum partition thicknesses

4 结 论

针对Al/PTFE 活性材料在冲击波加载条件下的响应特性问题，考虑Al/PTFE 活性材料的化学反应，通过拉氏实验分析方法，结合AUTODYN 有限元数值模拟，研究了Al/PTFE 活性材料在冲击加载条件下的压力演化、反应度演化以及冲击波传播速度等特征，得到以下主要结论。

(1)通过拉氏实验，获得了冲击波在Al/PTFE 活性材料中传播规律，在短距离传播过程中，冲击波压力存在明显的衰减。对于冲击波波速，在5 和10 mm 隔板厚度条件下，由于活性材料快速反应会呈现先上升后下降趋势。并且入射冲击波压力越高，Al/PTFE 活性材料对冲击波传播时速度的影响越明显。

(2)基于AUTODYN 有限元数值模拟，利用拉氏实验压力曲线标定了适用于Al/PTFE 活性材料的Lee-Tarver 三项式点火反应模型参数，并验证了该模型及参数的有效性。

(3)通过对500 mm 长的Al/PTFE 活性材料拉氏实验进行模拟，获得了冲击波压力和冲击波速度的演化规律，冲击波压力和冲击波速度分别趋于1.30 GPa 和2180 m/s，材料反应度趋于0.17。Al/PTFE 活性材料化学反应释能，有效阻止了冲击波传播过程的能量耗散，导致冲击波压力和冲击波速度的稳定值远高于材料强度和材料声速。