基于消卷积的三维成像雷达散射截面测量技术
2022-07-10任雯欣廖可非任浩田
任雯欣, 廖可非,2*, 任浩田
(1.桂林电子科技大学信息与通信学院, 桂林 541004; 2.桂林电子科技大学卫星导航定位与位置服务国家地方联合工程研究中心, 桂林 541004)
雷达散射截面积(radar cross section,RCS)是衡量目标在电磁照射下沿接收方向散射回波能力的物理量,表征了雷达目标的散射能力。它会随雷达的信号频率,极化方式以及入射角度的变化而变化,并且与目标的形状,大小,以及结构和材料有关[1]。随着科学技术的不断发展,对RCS的精确测量与预估提出了更高的需求。
传统的RCS测量主要分为室外远场测量[2-3]、室内紧缩场测量[4]和近场成像测量[5-6],但在实际测量中,远场测量条件不易满足,紧缩场测量价格昂贵,为克服测量距离的限制,基于近场成像测量技术得到了广泛关注,该种方法基于成像技术获得目标图像再提取图像中的散射中心[7-8],最终反演得到RCS。这些方法主要分为基于逆合成孔径雷达成像的RCS测量[9-10]和基于合成孔径雷达成像的RCS测量[11-12]。Broquetas等[9]提出了一种基于目标表面散射场聚焦算子的近场球面波ISAR成像算法。Lahaie[10]通过反射率近似值对目标散射进行建模以及逆合成孔径雷达(inverse synthetic aperture radar,ISAR)成像。Tulgar等[11]提出了一种聚束是SAR成像算法,通过获得目标的SAR图像再提取相应的RCS。Sensani等[12]介绍了一种由雷达图像的近场到远场(NF2FF)处理程序,有利于加深对RCS散射机理的理解。Kobayashi等[13]提出了一种改进的圆柱扫描的近远场变换方法,该方法使用了小球从精确积分方程中获得的聚焦因子,使在微波暗室中也可进行RCS测量。Wang等[14]设计了一个二维扫描系统,该系统可以获取目标的近场三维散射系数图像。许鑫等[15]提出了一种基于线性调频信号的压缩感知雷达成像算法,可得到高分辨的图像。目前基于成像的RCS测量已有广泛研究[9-17],但对合成孔径三维成像的RCS测量现在还没有广泛的研究和应用。进一步研究合成孔径三维成像的RCS测量更好分析RCS特征、旁瓣抑制以及提高成像质量对于RCS的精确反演有着重要意义。
基于传统的近场成像方法,由于旁瓣多是由假目标引起的,传统的消除噪声,抑制旁瓣的方法有阈值法和加窗法,然而,这两种方法都有局限性,会导致目标图像失真从而导致通过反演得到RCS缺乏分辨率。因此需要考虑用其他算法来有效抑制图像旁瓣。
基于上述问题,针对旁瓣抑制的三维成像RCS测量技术展开研究,提出了两种主要的抑制旁瓣的算法:一是基于改进CLEAN算法[18]的旁瓣抑制;二是基于压缩感知成像的旁瓣抑制方法。然后分别从抑制原理和仿真结果两方面对上述方法进行对比。
1 RCS测量模型
1.1 测量模型
采用线阵合成孔径的三维成像RCS测量模型为例进行说明,成像模型如图1所示。在三维坐标xyz下建立成像场景,在二维平面上通过阵元的移动,等效合成二维的平面阵列,同时结合宽带信号来获得目标的三维分辨能力。
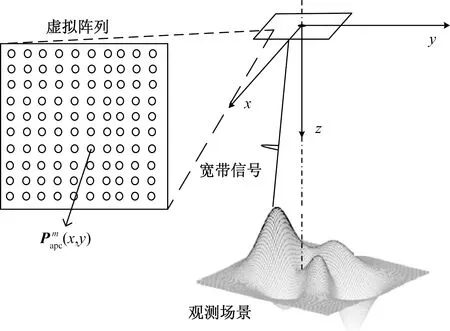
表示所形成的虚拟阵列的第m个阵元
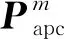
(1)
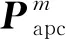
将式(1)回波信号写为矩阵形式,可表示为
Y=Φ
(2)
(3)
式(3)中:φmn为一个列向量,可表示为
(4)
后像投影成像BP可表示为
BP=ΦTΦ*
(5)
式(5)中:Φ*为式(3)矩阵Φ的共轭;ΦT为Φ的转置。
获得目标的三维成像后,从成像当中提取目标的散射中心,之后通过近远场变换得到远场的散射函数,最后通过定标法求解远场RCS,通过RCS反演,可以从三维合成孔径雷达(synthetic aperture radar,SAR)图像中恢复出目标远场不同角度、不同频率的RCS。
1.2 旁瓣分析
一般信号频谱中的旁瓣主要为有限长度信号的截断效应所带来的,雷达在一维距离像上,基于其有限的信号带宽,频谱函数近似为矩形函数,对其作逆傅里叶变换,即为Sinc函数,而Sinc函数含有旁瓣。同理,雷达在方位上也是等效合成了一定的方位带宽。因此雷达成像当中的旁瓣来源于有限带宽信号的截断效应,而截断效应会带来两个方面的影响,一个是泄露,具体表现在雷达成像中是理想分辨函数的展宽,从而降低了图像的分辨率。另一个是谱间干扰,由于旁瓣的影响,在雷达成像中会造成强点附近的弱目标被掩盖,或者误将强点的旁瓣当作目标。因此降低图像的旁瓣对成像质量的提高至关重要。传统的抑制旁瓣的方法有阈值法和窗函数法,加窗法通过加权系数,提高主瓣能量,降低副瓣能量,来降低有限信号带宽的截断效应。但是传统的加窗旁瓣抑制方法一定程度上会展宽主瓣,导致图像分辨率的降低,因此在分辨率和峰值旁瓣比上需要折中考虑。阈值法基于不同阈值提取散射信息,当阈值较小时,会将成像中的旁瓣信息提取出来,当阈值较大时,导致成像当中部分散射信息会丢失,造成RCS的反演误差。
2 基于旁瓣抑制的新方法
2.1 改进CLEAN算法旁瓣抑制的RCS测量
当场景目标变多变复杂时,利用传统CLEAN算法抑制旁瓣时误差较大,这极大的影响着RCS的测量精度,因此考虑采用改进的CLEAN算法抑制图像的旁瓣,来完成对目标散射中心的提取,提高RCS的测量精度。
改进CLEAN算法利用已有的估值信息,来逐个更新需要重估的点,从而提高估计精度,达到抑制旁瓣的目的。
PSFi表示第i个散射点在整个空间的BP像,可表示为
PSFi=Φ(·,i)TΦ*
(6)
式(6)为该点的点扩展函数,其中Φ(·,i)为矩阵Φ的第i列。
传统成像都是由真实的散射系数卷积上点扩展函数来获得也可以展开来写,即不同的散射系数乘上其对应的点扩展函数再求和,即
(7)
式(7)中:σi为第i个散射点的散射系数,σi=1;N为满足成像场景中的所有散射点个数。
改进CLEAN算法每次寻找的估计值,不仅影响着此次的精度,也影响着其余散射系数的估计精度,只有尽可能的将每次的估计误差变小,才能保证更好的估计其余的散射系数。假设获得了全场景的散射系数估计,则残差为
(8)
当迭代减法得到的“脏”图达到某一阈值或已经估计的散射点数达到设定的条件时,对这些点进行重新估计,并用重新估计的值,逐个更新其余的值,从而减弱相干CLEAN算法带来的累计误差。成像场景中各个点的BP像是由该点的像与其他目标在该点处的旁瓣干扰组成,改进CLEAN算法抑制旁瓣的过程就是消卷积的过程,散射系数与非理想点扩展函数的卷积运算会造成谱间干扰,强弱目标混淆,通过不断从“脏”图中寻找最大值,获得点散射系数估计,消去该估计的旁瓣影响。
2.2 压缩感知旁瓣抑制的RCS测量
传统的奈奎斯特时域等间隔采样,使得信号在频谱上进行周期延拓,如果采样率不满足信号带宽的两倍,则会发生频谱混叠,而压缩感知的非等间隔采样和随机稀疏采样使得频谱搬移不再是周期有序的搬移,使得频谱泄露的能量能随机和近似均匀的分布在整个频率轴上,不再产生周期有效的叠加和干扰。
压缩感知的成功应用,信号需要满足稀疏性,即“K稀疏”,对于一个Nd维离散信号,Nd个元素值中只有K个是非零的,其中K≪Nd,则称这个信号是K稀疏的。基于信号的稀疏先验假设,从稀疏域上经过非周期搬移后的信号即稀疏观测后的信号,在稀疏域上只有离散的少量峰值存在,压缩感知重构算法如匹配追踪算法就是从该信息中逐个求解出相应强点,再减去该点对应的干扰,从而可以从信号当中逐个恢复出有效的强散射信号,而恢复的过程中,将一些低于某个阈值或者在噪声电压水平附近的点舍去,即将其置之为零。
压缩感知抑制旁瓣的核心思想是通过反卷积消除点扩展函数的影响。以下通过表达式对压缩感知抑制旁瓣进行解释。
设某单散射点坐标为
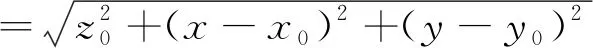
(9)
进行匹配滤波和距离徙动矫正并经去调频处理后得到的回波信号用卷积形式表示为
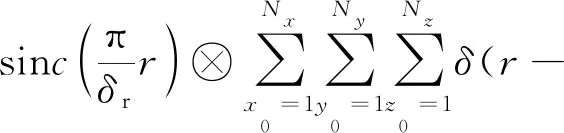
(10)
当信号具有稀疏特性时,可以利用压缩感知技术去除卷积核,对经过距离压缩之后的回波信号去除卷积核后进行方位向匹配滤波,利用1D-FFT获取水平方向压缩图像表达式为
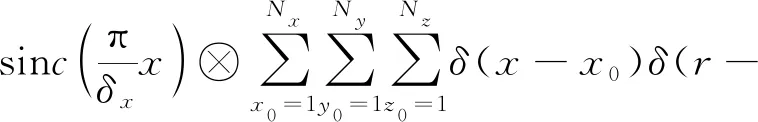
(11)
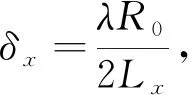
当信号具有稀疏性时,可除去卷积核。再对式(11)进行1D-FFT获取垂直方位向压缩图像得到
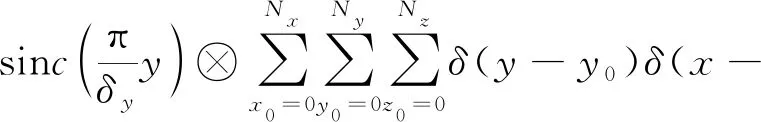
(12)
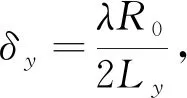
当信号具有稀疏性时,可除去卷积核后对式(12)进行重建,当场景目标散射系数足够稀疏时,可以完全消除3维点扩展函数的影响,可以在一定程度上抑制旁瓣。
通过对改进CLEAN算法与压缩感知算法旁瓣抑制原理上分析,得出了两种方式的相同与不同之处。两者抑制旁瓣的原理都是通过消卷积,消除点扩展函数的影响,而不同在于压缩感知恢复重建的过程是在对原始信号稀疏采样后进行的,该操作使得信号在稀疏域进行了非周期性的搬移,从而使能量泄露能近似均匀的分布在整个稀疏变换域中,在恢复重建的过程中,能以更高的精度求解出相应的散射系数。改进CLEAN算法抑制旁瓣过程是在循环中不断的减去信号所对应的干扰,并逐步的求解出散射系数,在含有旁瓣串扰的条件下进行对应点扩展函数的消除,而这造成了改进CLEAN算法的误差。因此压缩感知就会比改进CLEAN算法精度要高。
3 仿真与结果
为验证三维成像中改进CLEAN算法与压缩感知的处理效果,用MATLAB在三维场景中建立理想的6个散射点,其散射系数和相对于场景中心的坐标如表1所示,仿真中频率个数Nf为100,初始频率f0为1.5 GHz步进频率增量为10 MHz,横向阵元和纵向阵元个数都为21个。场景中心与接收阵列相距2 m。

表1 不同目标的坐标位置和散射系数
基于阈值法提取散射中心,后向投影成像算法(back projection imaging algorithm,BP)处理的图像、改进CELAN算法处理的图像分别如图2(a)、图2(b)通过压缩感知对散射系数的恢复如图2(c)所示。
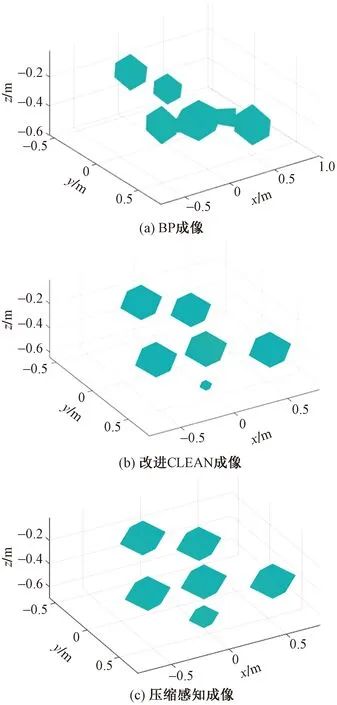
图2 基于不同算法对散射系数的恢复图像
可以看出,经过压缩感知算法和改进CLEAN算法对散射系数的回复效果较好,使得小散射点也能够分辨出来。
表2为改进CLEAN与压缩感知对散射系数的恢复误差。由下表可以看出压缩感知方法恢复的散射点精度相对于改进CLEAN算法来说有大大提升。
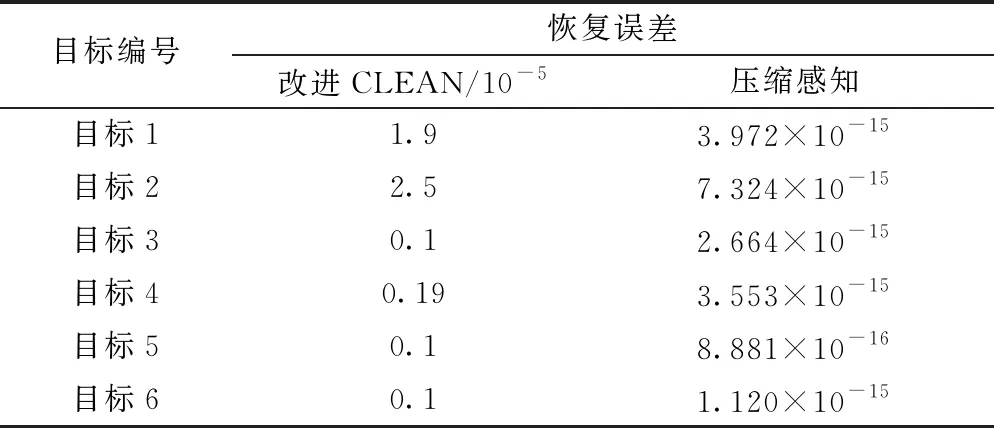
表2 不同算法对各个目标的恢复误差
通过FEKO仿真验证改进CLEAN算法和压缩感知算法对RCS反演的影响,并与传统的BP成像算法进行比较。用FEKO对如图3(a)所示的飞机模型进行求解。将3种算法所反演的RCS与参考值进行比较,具体仿真如下。
基于传统BP算法、改进CLEAN算法及压缩感知的飞机模型成像分别如图3(b)、图3(c)、图3(d)所示。
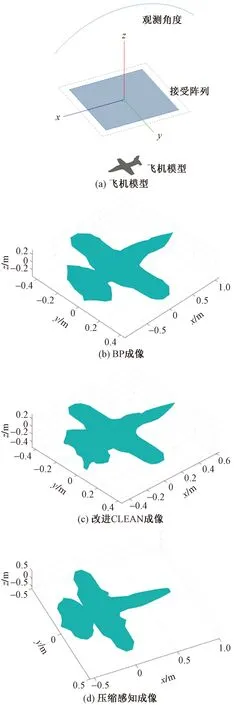
图3 飞机模型基于不同算法成像
中频处分别基于水平方位向x、垂直方位向y以及观测角度为零度时不同频率的RCS值,如图4所示。
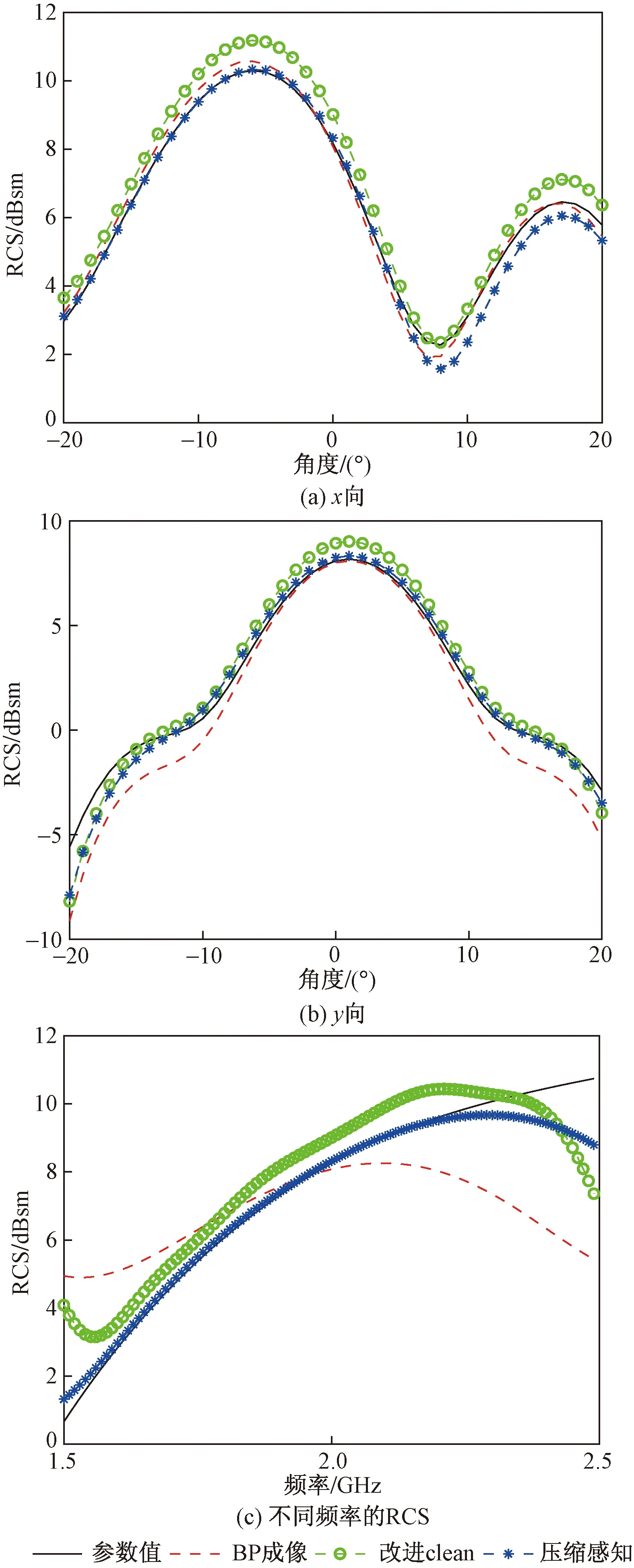
图4 x、y向观测角度及观测角度为零度时不同频率的RCS
由图4可以看出,基于压缩感知成像的RCS反演,其效果更加接近参考值。由于BP成像存在旁瓣效应,因此距离(z轴)方向的散射系数会相互串扰,其反演的RCS在不同的频率中有较大的误差。为便于观察3种方法与参考值的不同,如表3所示。
基于CS细分网格三维成像的RCS测量的采样间隔为(0.07 m,0.07 m, 0.07 m)。由表3可以看出,压缩感知细分网格成像所反演的RCS优于传统成像,针对飞机模型,在机尾处中间竖立的机翼,散射点较难提取,反演的角度RCS也会有误差。整体来看,基于压缩感知细分网格成像的RCS测量精度更高。尤其在距离向显著提升了不同频率的RCS反演精度。
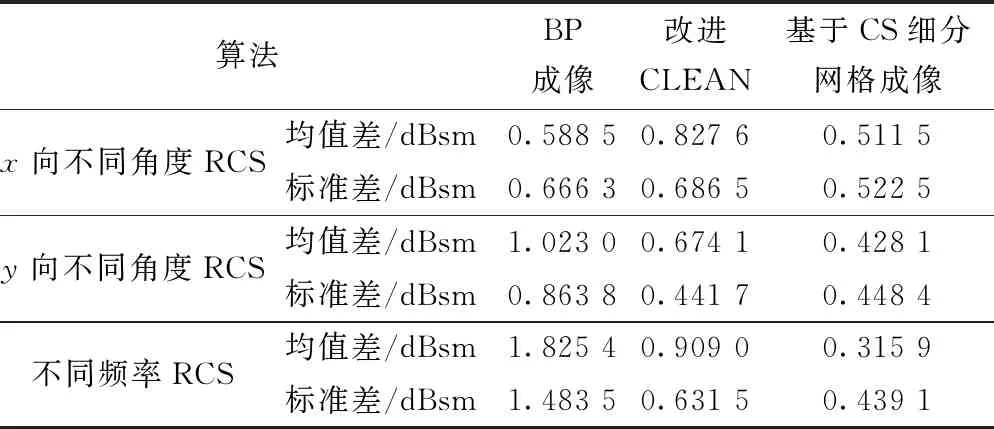
表3 不同算法对飞机RCS的均值差与标准差
4 结论
基于旁瓣抑制的三维成像RCS测量技术展开了具体研究,先详细介绍了合成孔径的三维成像模型,并给出了成像RCS反演的主要步骤。分析了基于成像算法产生旁瓣的原因;其次介绍了基于改进CLEAN算法以及压缩感知两种方法对成像旁瓣的抑制;最后基于不同算法对目标RCS反演进行仿真验证得出以下结论。
(1)改进CLEAN算法与压缩感知算法抑制旁瓣的原理都是消卷积的过程,目标RCS反演时,两者都会降低有限截断误差带来的效应。
(2)改进CLEAN算法与压缩感知算法都有效的抑制了图像的旁瓣,提高了RCS的测量精度。而基于细分网格的压缩感知有着相比于改进CLEAN算法更好的优势。该方式直接从信号入手,不需要额外成像或部分成像,该方式可以以远低于奈奎斯特的采样率对回波进行稀疏采样,当满足重构条件时,即可稳定而高精度地完成对目标像的稀疏重构,这对散射系数的精确提取和RCS的精确反演提供了有利的条件。
