运用偶函数性质优化解题

安徽省宿城第一中学 (234000) 陈玉龙

函数的奇偶性是函数的一个重要性质，本文通过典型实例的分析剖解，介绍偶函数几种性质特点的应用，旨在强化对偶函数性质的理解，提升所学知识的运用能力，供同行们参考.

一、关注偶函数的定义域

例1 已知二次函数f(x)=ax2+bx+c是定义在[a-1,,2a]上的偶函数，求此函数的单调增区间.

解析：由于f(x)是偶函数，则其定义域应关于原点对称，即有1-a=-2a，则，所以f(x)=-x2+bx+c，又由偶函数的定义得，在定义域内都有f(-x)=f(x)得-bx=bx成立，即有b=0，故f(x)=-x2+c，所以函数f(x)的单调增区间为(-∞,0].

评注：函数的定义域关于原点对称是函数为“奇函数和偶函数”的必要条件，此条件比较容被忽视，必须进行强化.

例2 已知函数f(x)是偶函数，且在(0，+∞)上单调递增，若f(-1)=0，试求关于x的不等式xf(x)<0的解集.

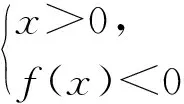
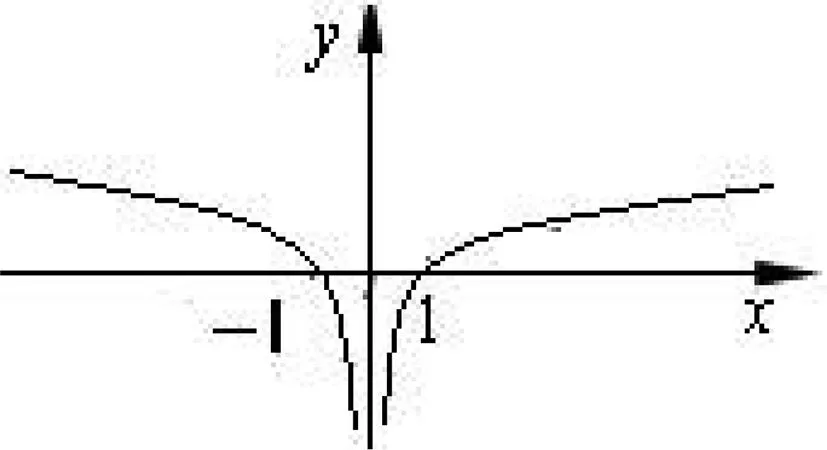
图1

评注：考虑到偶函数的定义域关于原点对称，则由给出的部分单调区间可推出整个函数的定义域和单调性，再抓住特殊点，就能够勾画出函数的大致图像，这样成功解题就是比较容易的事了.

二、关注f(-x)=f(x)的应用

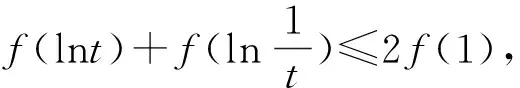
评注：由f(-x)=f(x)一般常用来判断一个函数是否是偶函数，而本例中反用此性质化简所给的不等式，从而显露出解决的机会.

例4 设a为非零实数，偶函数f(x)=x2+a|x-m|+1(x∈R)在区间(2,3)上存在唯一的零点，求实数a的取值范围.

评注：根据偶函数的性质解决了所给表达式中的参数，为下一步的解题扫清了障碍，这是成功解题的重要一环.

三、关注偶函数图象关于y轴对称

例5 若f(x)是R上的偶函数,且满足f(x+2)=f(x)，当x∈[0,1]时,f(x)=2x.若在区间[-2,3]上方程ax+2a-f(x)=0恰有四个不相等的实数根，求实数a的取值范围.

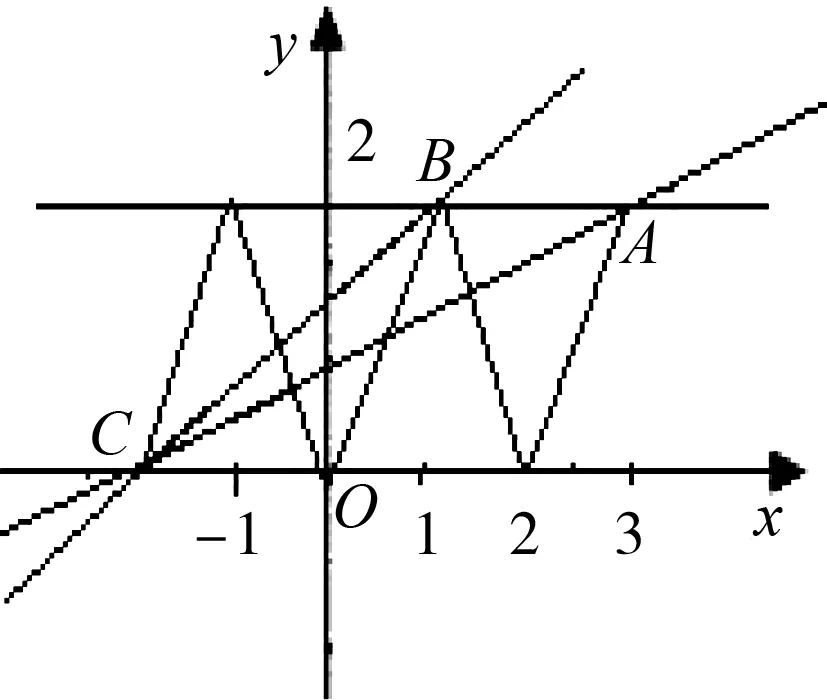
图2

评注：偶函数的图像关于y轴对称是函数的重要几何性质，在涉及画图像时必须关注几何性质的运用，本题中，根据此性质画出整个函数图像是解题的成功的关键.

例6 定义在R上的函数在(-∞,a]上是增函数，函数y=f(x+a)是偶函数，当x1a，且|x1-a|<|x2-a|时，试判断f(2a-x1)与f(x2)的大小关系.

解析：由于函数y=f(x+a)是由y=f(x)向左平移a个单位所得，而y=f(x+a)是偶函数，所以y=f(x)的函数图像关于x=a对称.又在(-∞,a]上是增函数，故在(a,+∞)是减函数，当x1a，且|x1-a|<|x2-a|时，去掉绝对值符号得a-x1a，x2>a，由在(a,+∞)是减函数得f(2a-x1)>f(x2).

评注：通过研究给出的偶函数条件，判断出函数y=f(x)的图像的对称性，这是判断两个函数值大小的关键举措，此处显示了图像性质的对于解题的重要性.

四、关于f(x)=f(|x|)的应用

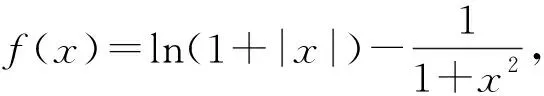
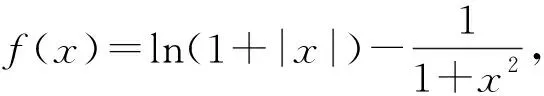
点评：通过判断出函数的单调性与奇偶性后，就将一个隐含关系转化为一个简单的绝对值不等式，充分发挥了隐含的偶函数条件的解题作用.

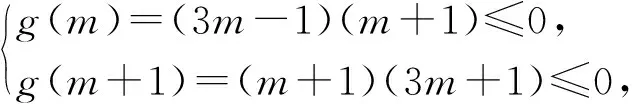
评注：这里通过运用f(x)=f(|x|)和函数的单调性，将待求的函数不等式转化为绝对值不等式，成功地避免了分类讨论所引起的不方便.

在我们的解题教学中，要帮助学生挖掘一些概念和性质的用途，尤其是如何运用它们去优化解题，通过在我们的课堂上示范和归纳，可以起到率先垂范、画龙点睛的作用.