分数阶优化的鸽群图像分割算法

李光昊 马瑜 郭姝琪 王仕儒

（宁夏大学物理与电子电气工程学院 宁夏回族自治区银川市 750021）

1 引言

在计算机视觉中，图像分割是图像处理的重要组成部分，其目的是将目标区域和背景区域分离。阈值分割是一类常用的图像分割方法，其中最大类间方差法（Otsu）因其原理简单、易于实现，被广泛应用于图像分割。二维Otsu 算法相对原始 Otsu 算法很好地提升了分割效果，但计算耗时长，收敛速度慢。张建波等人利用二维灰度梯度直方图对算法进行优化，有效降低了运算复杂度，提高了分割精度。李鹏等人利用麻雀算法优化Otsu 分割算法，大幅提升了算法效率。

仿生群体智能优化算法是通过模拟自然界中事物或生物的运动和行为规律所提出的一种算法，常用来解决寻优、参数优化等问题，但也存在收敛速度慢、易陷入局部最优等问题。鸽群算法是一种受鸽子归巢行为启发而产生优化算法（pigeon-inspired optimization, PIO），最早由段海滨教授提出，近年来在群体智能优化领域受到广泛应用。林娜等提出了自适应权重的鸽群算法，一定程度上改善了收敛速度慢的缺陷。

近年来，分数阶微积分作为一种数学工具，被广泛应用于图像处理。2010 年，Pires等最早将分数阶算法引入PSO 算法中，验证了算法的收敛速度与分数阶阶次密切相关。魏晶茹等提出了一种自适应的分数阶粒子群算法，利用分数阶粒子群算法进行图像分割，取得了很好的分割效果。Yashar Mousavi等将分数阶与萤火虫算法结合，同样获得了较好的实验结果。

本文针对鸽群算法在图像分割中具有的收敛速度慢和寻优精度低的缺点，将分数阶微积分引入到鸽群算法中，对鸽群算法的速度更新进行优化，克服其容易陷入局部最优的缺陷。并引入分数阶增强滤波对图像进行预处理，提高分割精度。在鸽群算法寻优中引入混沌搜索算法，提高全局搜索能力，结合二维Otsu 分割算法确定最佳分割阈值，加快算法收敛速度。

2 分数阶混合鸽群算法

2.1 传统鸽群算法

鸽群优化算法是模仿鸽群归巢而建立的一类仿生优化方法。鸽群归巢过程中，会根据情况使用不同的导航方式，当鸽群距离巢穴较远时主要采用磁场导航，而接近巢穴时则主要根据地标对路线进行修正。

2.1.1 磁场算子

在磁场算子阶段，鸽群的搜索具有全局最优特性。鸽群在多维搜索空间中，位置和速度根据下式进行更新：

上式中，X是位于中心的鸽子的位置，f(X(t))为当前鸽子的适应度函数值，即目标函数。

舍弃函数为：

在依靠地标算子寻优的过程中，适应度低的鸽子对地标不熟悉，具有较差的寻优能力，因而被舍去，其余鸽子跟随高适应度的鸽子进行移动，每次迭代都会舍弃一半的鸽子数量。

2.2 分数阶微积分

分数阶微积分即为阶次是分数的微分和积分，是对传统微积分的延伸，由于其具有记忆性，在数字信号处理、数字图像处理等领域具有广泛的应用。分数阶微积分有多种定义，其中最常用的是G-L（Grumwald-Letniko）定义。

假设在区间[a,b](a＜b,a∈R,b∈R)内存在连续可导的函数f(x)，则f(x)的一阶导数为：

2.3 分数阶优化的鸽群算法

原始鸽群算法存在收敛速度慢，容易陷入局部最优的缺点，为了提升寻优效率和精度，将分数阶微积分引入鸽群算法中，提出分数阶优化鸽群算法（fractional-order pigeoninspired optimization, FPIO）。该算法将分数阶微积分引入原始鸽群算法速度更新公式，利用分数阶微积分的记忆性和遗传性提升鸽群算法的收敛速度，并且能够有效的改善原始鸽群容易陷入局部最优的问题。将式（1）变形为：

上式中，d是鸽群的全局最优位置与其他鸽子距离的平均值，鸽子间平均距离最大值为d，最小值为d，则f∈[0,1]。根据文献可以得到，当分数阶次α∈[0.5,0.8]时，算法效果最好，因此可将α 根据下式进行动态调整：

2.4 混沌搜索算法

混沌是一种无规则的运动状态，因其具有随机性、遍历性和规律性，常用于寻优问题。钱伟懿等人利将混沌序列引入群体智能算法的研究，提高了算法的搜索速度。李娟等人利用混沌序列对种群进行初始化，提高了种群的搜索能力。

本文所采用的混沌映射为Logistic 映射，其表达式为：

在每次迭代中，用混沌搜索得到的最优位置随机取代一只鸽子，这样可以有效地提升种群多样性，提升算法搜索能力。

3 基于分数阶混合鸽群优化的Otsu分割算法

3.1 基于灰度-梯度的二维Otsu阈值分割算法

Otsu 算法最早由日本学者提出，主要原理是将图像分为目标类和背景类，两类间的类间方差越大，图像分割效果越明显。基于灰度-梯度直方图的二维Otsu 算法，一定程度上改善了原始Otsu 算法运算缓慢的缺陷，目前是比较常用的图像分割算法。

设图像总像素点数为N，n为灰度i、梯度j 的像数点数，其出现的概率为：

3.2 分数阶增强滤波

在数字图像增强处理中，分数阶微分增强滤波可以提升高频信号，同时更好地保留中低频信号，也即在增强图像纹理信息的同时，保留住图像中的平滑部分。本文引入分数阶增强滤波，对图像进行预处理，提升分割精度。滤波模板如图1。

图1： 分数阶滤波模板

式（29）所得到的fe(m)即为滤波模板中实际系数，对图像进行卷积滤波，可以实现对图像的增强。增强后的图像具有更清晰的纹理细节，使图像分割后保留住更多细节信息

3.3 基于分数阶混合鸽群优化的Otsu算法

针对原始的鸽群优化的二维Otsu 图像分割算法（PIOOtsu）收敛速度慢的问题，将分数阶引入鸽群算法速度更新公式，提出了分数阶混合鸽群的二维Otsu 图像分割算法（FPIO-Otsu），令二维Otsu 算法的离散度矩阵作为FPIO的适应度函数，算法的流程图及步骤如图2 所示。

图2： FPIO-Otsu 算法流程

步骤1 输入图像，对图像进行分数阶增强，基于二维Otsu 算法生成目标函数。

步骤2 确定初始的位置X，鸽子总数G，初始速度V，总的迭代次数N 以及磁场模型的迭代次数N。

步骤3 计算得到每个点的适应度f(x)。

步骤4 将该点的f(x)与该点的历史最佳位置对比，取较大者作为该点的历史最佳位置。

步骤5 将该点的f(x)与全局最优位置对比，取较大者作为当前全局最优位置。

步骤6 在前N_0 次迭代中，使用式（1）和式（2）来进行更新点的速度和位置；在N_0 次后使用式（4）来进行位置的更新。根据式（16）和式（17）进行混沌搜索，用搜索到的最优位置随机取代一只鸽子。

图3： Baboon 图像及分割结果

图4： Lena 图像及分割结果

步骤7 重复步骤3～步骤6，直到迭代N 代后，迭代停止，得到最佳阈值进行图像分割。

步骤8 输出分割后的图像。

4 实验结果及分析

为了验证本文算法的有效性，本文对不同类型的经典图像进行了仿真实验，并将本文算法（FPIO-Otsu）、分数阶粒子群优化的二维Otsu 算法（FPSO-Otsu）、原始鸽群优化的二维Otsu 算法（PIO-Otsu）在分割效果上进行对比。算法的硬件运行环境为Inter（R） Core（TM） i7-10875H CPU 2.30GHz，16GB 内存，软件编程语言为Matlab R2019a。

图5： lung 图像及分割结果

4.1 主观视觉分割结果

从图3 至图6 的分割结果对比可以看出，Baboon 图像中，本文算法对胡须部分的分割细节明显好于另外两种算法。Lena 图像中，本文算法对人物头发部分的纹理细节分割更加精细。lung 图像中，本文算法对肺组织病变区域的分割更清晰。Flower 图像中，本文算法在花瓣部分能分割出更多细节。

图6： Flower 图像及分割结果

4.2 客观评价指标

本文选取算法收敛时的迭代次数作为算法收敛速度的评价指标，迭代次数少则算法收敛快。同时采用峰值信噪比（PSNR）和结构相似性（SSIM）作为评价图像分割效果的客观评价指标。PSNR 值越大，算法抗噪性能越好。SSIM值越大，说明分割图像与原始图像更相似，分割精度更好。

由表1 的数据可以看出，本文算法对Baboon 图像的分割经过6 次迭代达到收敛，比另外两种算法收敛更快。而SSIM 以及PSNR 值均高于另外两种算法，可见本文算法提升了图像分割的准确度，抗噪性能也得到了保障。

表1： 三种算法对Baboon 图像分割结果对比

由表2 的数据可以看出，对Lena 图像本文算法仅经过6 次迭代找到了最佳阈值，而另外两种算法分别经过了10次以及14 次迭代，说明本文算法收敛速度更快。本文算法的SSIM 以及PSNR 值均高于另外两种算法，说明本文算法分割图像的准确度和抗噪性能都得到了提升。

表2： 三种算法对Lena 图像分割结果对比

由表3 的数据可以看出，对lung 图像，本文算法经过3次迭代达到收敛，另外两种算法分别经过59 次和16 次，说明本文算法收敛速度得到了较大提升。，本文算法的SSIM和PSNR 值同样高于另外两种算法，说明抗噪性能较强，分割细节较好。

表3： 三种算法对lung 图像分割结果对比

由表4 的数据可知，对Flower 图像的分割结果，本文算法的PSNR 值比另外两种算法高0.0758，SSIM 值比另外两种算法高0.006，说明本文算法分割效果好于另外两种算法。迭代次数上，本文算法经过4 次迭代达到收敛，另外两种算法分别经过23 次和14 次，说明本文算法收敛速度较快。

表4： 三种算法对Flower 图像分割结果对比

为了进一步验证本文算法对不同图像的分割效果，选取另外36 幅人物图像、32 幅景物图像以及20 幅医学图像，采用上述三种算法对其进行分割，将结果取平均值，受篇幅限制，部分分割结果如图7 所示。

图7： 对人物图像分割结果

图8： 对景物图像分割结果

从图7 至图9 的分割结果可以看出，本文算法对人物、景物、医学图像均从主观视觉上保证了分割的精度。从表5至表7 的数据可以看出，对人物图像，本文算法迭代次数较PIO-Otsu 和FPSO-Otsu 分别减少了68.99%和34.99%，SSIM 值分别提升了12.67%和3.67%，PSNR 值分别提升了9.83%和1.37%。对景物图像，本文算法迭代次数较PIOOtsu 和FPSO-Otsu 分别减少了70.17%和36.34%，SSIM 值分别提升了5.94%和5.33%，PSNR 值分别提升了1.79%和1.68%。对医学图像，本文算法迭代次数较PIO-Otsu 和FPSO-Otsu 分别减少了74.44%和47.93%，SSIM 值分别提升了1.49%和1.39%，PSNR 值分别提升了0.84%和0.81%。

图9： 对医学图像分割结果

表5： 36 幅人物图像平均分割结果对比

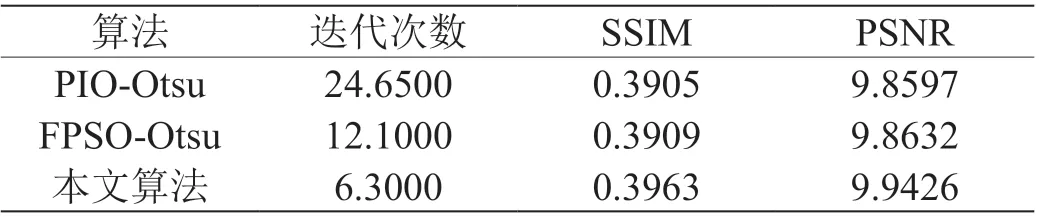
表7： 20 幅医学图像平均分割结果对比

表6： 32 幅景物图像平均分割结果对比

综上所述，本文算法无论是从主观视觉还是客观评价指标都提升了分割效果，收敛速度获得了较大提升。

5 结束语

本文提出的基于分数阶混合鸽群优化的二维Otsu 图像阈值分割算法，通过将分数阶与鸽群优化算法结合，并引入分数阶增强滤波和混沌搜索算法，使得鸽群个体更快地找到最优点，提高了收敛速度。本文算法从主观视觉和客观评价指标两方面的分割效果均优于传统算法，与传统鸽群优化的二维Otsu 算法相比，收敛速度提升约71.20%，与分数阶粒子群结合的二维Otsu 算法相比，收敛速度提升约39.75%，说明本文算法收敛速度更快。本文算法的PSNR 值相较于两外两种算法提升约4.15%和1.48%，SSIM 值提升约6.7%和3.46%，说明本文算法在提升收敛速度的同时，也取得了良好的分割效果。