基于Duane 模型的加速可靠性增长试验研究

孙强 王宏 臧伟旺

（中国电子科技集团公司第十四研究所 江苏省南京市 210039）

可靠性增长就是通过不断地消除产品设计或制造中的薄弱环节，使产品的可靠性随时间逐步提高的过程。可靠性增长是保证复杂系统投入使用后具有所要求的可靠性的一种有效途径，贯穿于系统寿命周期的各个阶段。可靠性增长试验的目的是通过“试验—分析—改进—再试验—再分析—再改进”（TAAF）解决设计缺陷，提高产品可靠性，具有如下特点：

（1）可靠性增长试验是工程研制阶段单独安排的可靠性工作项目（GJB 450A-2009 工作项目403），旨在通过试验及相应的分析改进，使产品的可靠性得到有计划的增长；

（2）可靠性增长试验是一种工程试验；

（3）可靠性增长试验本身不能提高产品的可靠性，只有进行设计、工艺改进，消除薄弱环节，才能提高产品固有可靠性；

（4）可靠性增长试验条件通常模拟产品的实际使用条件；

（5）可靠性增长试验时间通常取产品MTBF 目标值的5 ～25 倍（取决于可靠性增长模型、工程经验和产品规范）。

（6）成功的可靠性增长试验可以代替可靠性鉴定试验。

通常情况下，安排可靠性增长试验的时机是在工程研制阶段后期、可靠性鉴定试验之前。因为在这个时期，产品的功能性能已基本达到设计要求，产品已接近或达到设计定型技术状态；同时，由于产品尚未定型并投入大批量生产，故障纠正还有时间，还来得及对产品设计和制造工艺进行改进。

上世纪90 年代，我国在元器件和相关领域开展了相应的可靠性增长工作，通过大量的可靠性增长试验研究，暴露出很多潜在的故障问题，同时消除了多种故障隐患，有效地提高了整机产品的可靠性水平，取得了很多宝贵的理论和实践经验。

可靠性增长试验是反复试验、反复改进的TAAF 过程，产品的可靠性水平在不断地变动、提高，因此传统的恒定故障率的假设以及相应的数学分析方法已经不再适用，需要用更加科学的可靠性增长数学模型来描述和分析。对可靠性增长过程进行建模，是运用数学模型来定量地描述增长过程的一种方法，借助增长模型，可以预先分析可能的增长趋势并制定增长计划，跟踪增长过程，了解实际增长趋势及评估增长结果。

加速可靠性增长试验既能节省研制时间与经费，又能用合理而科学的方法评定经此试验后雷达设备的可靠性，规范的可靠性增长试验甚至能够代替可靠性鉴定试验。

1 Duane模型

产品的可靠性增长模型反映了产品可靠性在变动中的增长规律，利用可靠性增长模型可以及时评定产品在变动中任意时刻的可靠性状态。1962 年，通用电气工程师J.T.Duane在撰写的一份研究报告中指出，通过对两种液压装置及三种飞机发动机将近600 万台时的试验数据进行分析发现，只要不断地对产品进行改进，累积失效率与累积试验时间在双对数坐标纸上是一条直线，这一结论构成了Duane 模型的雏形。随后用了十多年的时间对大量可修电子产品的数据进行分析后认为产品可靠性基本符合这一规律，此后Duane 模型便得到了广泛应用。1978 年，Duane 模型被标准MII-SID-1635 采纳，并随后在1984 年和1987 年相继被手册MIL-HDBK-338 和MIL-HDBK-781 引用。

杜安模型是最常用的模型，这种模型可以图示的方法给出被度量的可靠性参数的变化及可靠性参数的估计。通过数据分析，产品的累计故障率与累积试验行时间在双对数坐标纸上能拟合成一条直线。Duane 模型的优点为模型参数的物理意义容易理解，便于制定可靠性增长计划，同时模型表示形式简洁，可靠性增长过程的跟踪和评估非常简便。

Duane 模型的数学描述如下：

式中：α—尺度参数，α＞0，与初始的MTBF 值和预处理有关；t—累积试验时间，单位为小时，当多台产品严格同步时，t 为多台的累积试验时间，尺度参数α 的意义：其倒数是Duane 模型累积MTBF 曲线在双对数坐标纵坐标的截距，从一点程度上反映了产品进入可靠性增长试验时初始MTBF 水平；m—增长系数，通常情况下，m＞0 时，产品可靠性水平随累积试验的增加而增长，又称正增长；当m＜0 时，产品的可靠性水平随累积试验时间的增加而下降，称负增长。增长率m 的意义：它是MTBF 曲线的斜率，反映了MTBF值随时间增长的速度。可靠性的增长率m 的一般可能范围在0.3 ～0.6 之间，m 在0.1 ～0.3 之间，表明改正措施不太有力；而m 在0.6 ～0.7 之间表明在实施增长试验过程中，采取了强有力的故障分析和纠正措施，是增长率的极限。

M(t)—累积MTBF，是考虑了母体变动下的含有产品MTBF 变动信息的一个统计量，从中可以提取产品的MTBF变动信息。M(t)的定义如下：

其中，r(t)-为到累积试验时间为t 时的累计故障数。如果试验过程中不对任何故障进行纠正而仅仅是排除故障，则由于母体未发生变化，M(t)就是下列的M(t)；M(t)—瞬时MTBF，是指在累积试验时间t 时，产品实际达到的MTBF，即如果试验在t 时刻停止，今后生产的产品以t 时刻的产品结构为准，则产品的MTBF 即为M(t)。

1.1 数据准备

对于不同的评估对象，列出相关故障的故障时间序列，假设n 个故障发生时间按序排列分别为t,t,…,t。对于单台试验，t即为故障发生时的累积试验时间；对于多台同步试验，t为发生故障的那台试验样机的累积试验时间与未发生故障的剩余试验样机为处理该故障而停止作业时的累积试验时间之和。

计算这些故障时间相对应的累积MTBF 值，得：

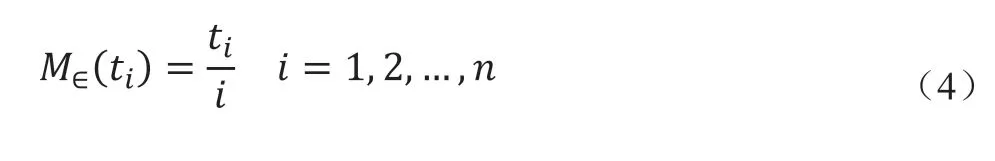
1.2 最小二乘法线性拟合

1.3 MTBF评估

采用外推法评定试验结束后、今后按试验结束时的结构状态生产的产品的MTBF，利用下式计算：

2 加速因子计算

加速因子是加速可靠性增长试验中一个重要参数，其定义为：若令某产品在正常应力水平S的寿命分布函数为F(t)，t为其p 分位寿命，即F(t)=p，且令该产品在加速应力水平S下的寿命分布函数为F(t)，t为其p 分位寿命，即F(t)=p，则两个p 分位寿命之比为：

式中：W—实际试验剖面的随机振动应力的功率谱密度，单位为g/Hz；W—加速试验剖面的随机振动应力的功率谱密度，单位为g/Hz；T—实际试验剖面的等效振动时间，单位为h；T—加速试验剖面的实际振动时间，单位为h；b—模型参数，随机振动时b=4。

在计算加速因子时，如果试验剖面存在多个振动应力水平，则需要先计算将所有应力折算至同一水平下的等效时间，再计算加速因子。根据下式计算振动加速因子。

表2： 加速下的失效时间与换算成实际应力下的失效时间

表3： 换算成实际应力下的失效时间与处理后的失效时间

3 应用案例

某电子设备实际的振动应力水平分别是振动1、振动2和振动3，每个循环第120min、232min、360min 先后施加振动1、振动2、振动3。具体如表1 所示。

表1： 不同振动类型持续时间

3.1 加速可靠性增长试验剖面

由于振动应力是主要影响因素。因此，试验中主要选取振动应力作为加速应力，通过提高振动应力量级以缩短增长试验的试验时间。如图1、图2 所示。

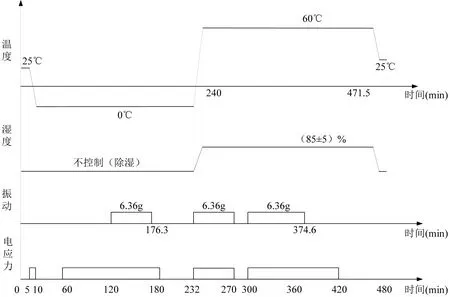
图1： 加速可靠性增长试验剖面（X 向/Z 向）

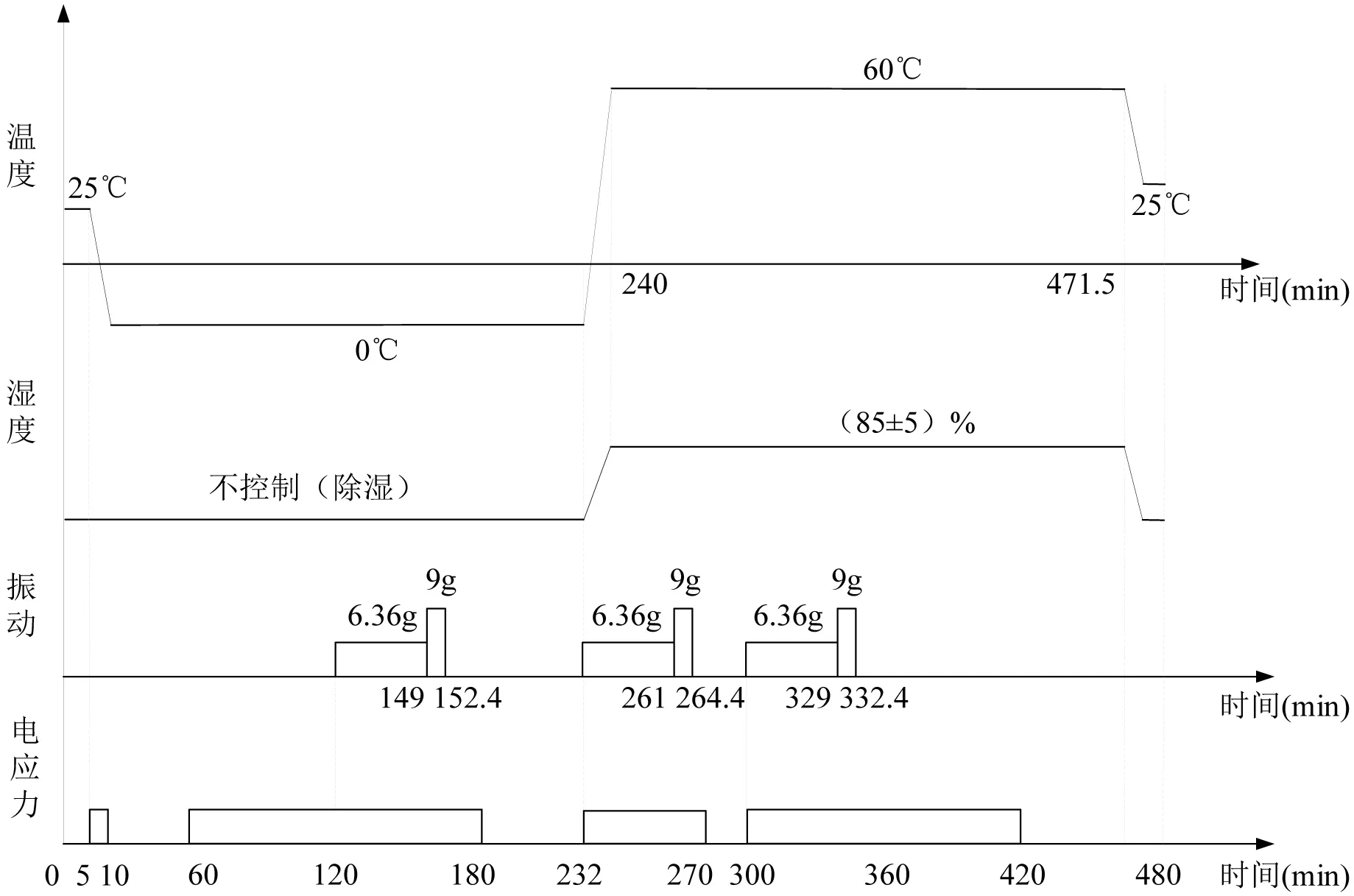
图2： 加速可靠性增长试验剖面（Y 向）

3.2 可靠性评估

3.2.1 加速因子计算

由于在实际应力下的可靠性增长试验剖面中，振动应力有三种，分别是3.18g、6g 和9g（转换为功率谱密度），且它们各自持续的时间不相同，难以直接进行计算。所以，先把实际应力水平下的三种振动应力的振动时间进行归一化处

4 结束语

加速可靠性增长试验采用较产品正常使用状态下所经受的更加严酷的试验条件，通过在有限时间内搜集更多产品寿命与可靠性信息。加速可靠性增长试验既能节省时间与经费，又能用合理而科学的方法评定经此试验后设备的可靠性，规范的可靠性增长试验可代替可靠性鉴定试验。本文采用加速因子和Duane 模型对产品的加速可靠性增长试验进行了定量评估，并通过典型应用案例对评估方法进行了验证。