基于TCN 的车辆跟驰轨迹优化模型

吕炎明 赵治宇 郐世扬

（北京交通大学软件学院 北京市 100091）

1 引言

自动驾驶技术是基于人工智能、道路勘测等技术于一体的综合技术，是当前道路交通科学研究领域绕不开的热门课题，基于该技术的各种特定场景下的优化模型层出不穷。汽车跟驰(Car-Following, CF)是该研究领域的核心场景之一，也是道路交通过程中最普遍存在的情况，汽车跟驰的主要任务是控制车速以保持安全舒适的跟车间隙。汽车跟驰的速度与间隙控制有利于减轻驾驶员的工作量、改善交通安全并增强道路通行能力。而通过模仿人类驾驶车辆的跟驰行为，应用自动驾驶技术的汽车可以习得一定车辆跟驰能力。

基于该命题的研究，科学界已经有比较清晰的研究方向和相对成熟的解决方案，其大多将场景定义为时序问题，利用RNN 等循环神经网络来训练智能体，因为RNN 天生的循环自回归的结构是对时间序列的很好的表示。Alahi 等首次提出RNN 的变体，基于长短时记忆(Long Short Term Memory, LSTM)的轨迹预测方法，将轨迹设立为一种时序问题，根据过去一段时间步长的轨迹序列预测未来的轨迹。Zhang 等通过使用LSTM，将车辆的跟驰行为(CF)与换道行为(Lane-Changing, LC)同时进行建模，提出了一种不同于多次训练LSTM 模型(Retrained LSTM)的混合再训练约束(HRC)方法来进一步优化LSTM 模型。刘创等人提出将LSTM 网络处理的车辆历史轨迹信息作为全局特征，通过卷积池化来提取信息用于轨迹预测。Cho等提出了改良RNN的门控循环单元(Gated Recurrent Unit, GRU)。Wang等提出利用GRU 对汽车跟驰行为进行建模，考虑驾驶员的记忆因素，并将其引入到模型中。费蓉等提出建立新的一种基于GRU 的车辆跟驰模型，获得了较好的仿真度与稳定性。

与之相比，传统的卷积神经网络(Recurrent Neural Network, RNN)一般被认为不太适合时序问题的建模，这主要由于其卷积核大小的限制，不能很好的抓取长时的依赖信息。由此，传统的卷积网络并没有被用来解决车辆跟驰问题。但近年来，由Bai 等提出的基于因果卷积、空洞卷积和残存链接的时序卷积神经网络(Temporal Convolutional Network, TCN)可以被用来解决时序问题，并且在许多应用场景上取得了与RNN、LSTM、GRU 等循环神经网络同等甚至更优秀的表现。于是我们提出了将TCN 引入自动驾驶领域并将其应用于车辆跟驰模型的研究，并通过实验比较说明其与许多得到广泛应用的传统循环神经网络建模方式在相同场景下的表现差异。

本文的剩余部分组成如下：第二节详细介绍了车辆跟驰模型，TCN 网络的组成结构及项目采用的数据集NGSIM；第三节研究了本文网络模型的输入输出，网络参数及数据处理，并使用数据集中的i-80 路段对模型进行训练和评估，通过us-101 路段的数据及HighD 数据集的数据研究了模型的泛化能力；第四节研究总结了项目的主要结论及未来的研究方向。

2 项目背景

2.1 车辆跟驰(Car Following)

跟驰模型描述了跟驰车辆(Following Vehicle, FV)响应引导车辆(Leading Vehicle, LV)的动作的运动，它们是微观道路交通场景的重要组成部分，并且为自动驾驶车辆跟驰系统的理论提供了参考。早期的车辆跟驰模型是纯数学演算的公式模型，该模型存在车辆跟驰的效率低、车辆行为预测效果差等特点。近年来，得益于人工智能技术的飞速发展，深度学习、强化学习等技术常应用于车辆跟驰模型的研究，取得了一定进展，目前主要应用的神经网络模型有RNN、LSTM、GRU 等。

2.2 时序卷积神经网络(TCN)

时序卷积神经网络(TCN)是卷积神经网络(CNN)的一种，是基于因果卷积(Causal Convolution)、空洞卷积(Dilated Convolution)和残差链接(Residual Connections)的一种新型神经网络。

2.2.1 因果卷积

TCN 有两个重要特征，一是其具有相同的输入和输出长度，二是其模型预测只会受到历史数据的影响而不会受到未来数据的渗透，后者是卷积网络用于解决时序问题的关键。因果卷积可以用（公式1）直观表示。即对卷积网络中每一层t 时刻的权重变化p 只来自其上一层的t 时刻及之前时刻节点的p 权重变化。作为一种单向的网络结构，其存在使得整个卷积网络的训练是以数据的时间属性为基准，不会出现未来影响过去的情况，是一种严格的时间约束模型，因此被称为因果卷积。

Causal Convolutions:

公式 1 因果卷积

2.2.2 空洞卷积

传统神经网络不能被应用于时序问题的重要原因，是建模基于的时间步长受限于卷积核的大小，如果要想抓取更长的依赖关系，就需要线性的堆叠很多的网络层，使得网络体积过大或很难收敛。为了解决这一问题，TCN 采用了空洞卷积的方式，即通过对输入数据指数级逐层间隔采样，从而实现用较少的网络层数获得较大的感受野，具体的实现方法如（公式 2）所示，其中F 是我们定义的对序列元素s 的卷积运算，f 是一个过滤器，k 是过滤器的大小，d 是我们给定的扩张因子，s-d·i 说明过去的方向。（图1）也能很好地说明该卷积方式。

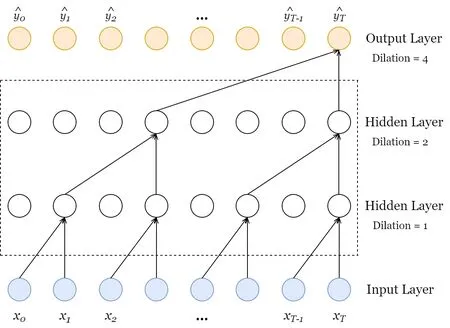
图1： TCN 网络的空洞卷积结构

Dilated Convolution:

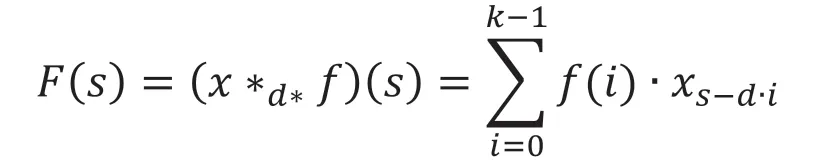
公式 2 空洞卷积

2.2.3 残差链接

对于深层的神经网络，随着网络深度的不断提高，获取的信息量会逐层减少。TCN 通过构建残差链接来实现网络结构中跨层的传递信息，防止信息丢失。在本网络结构中，我们添加了一个残差块(Residual Block)以替代一层卷积。残差块拥有两层的卷积和非线性映射，对于残差块中的每一层，我们添加了Dropout 层并进行了权重值归一化处理来将网络正则化，提高网络的泛化能力。

2.3 下一代仿真模拟数据集(NGSIM)

随着智能交通系统的发展，NGSIM(Next Generation Simulation)数据集是美国FHWA 搜集的美国高速公路行车数据。数据集采集于美国的四个不同地区，分别是加州南向的US-101 号公路，加州洛杉矶的Lankershim Boulevard 地图，加州埃默里维尔的东向的 I-80 号公路，以及佐治亚州亚特拉大的Peachtree Street。该数据集覆盖了结构化道路的路口，高速上下闸道等车路协同研究的热点区域。其数据是采用摄像头获取，得到了道路上的所有车辆在一个时间段的车辆行驶状况。再通过对原始的视频信息做后处理，加工成一条一条的轨迹点记录，生成了交通流中每辆车的行驶轨迹数据。我们的项目依托NGSIM 进行数据的分析和问题的研究。

3 实验研究

我们的实验聚焦简单跟驰场景下不同网络(TCN 和RNN、LSTM、GRU)之间的预测准确性、收敛速率与泛化能力。在实验场景一致的前提下，网络中的各个非核心参数尽量保持统一，并通过实验选取该场景下最优的核心参数，以保证该网络在给定场景下的预测准确性达到最高。

3.1 模型输入输出

为研究简单跟驰场景下后车根据跟驰前车时对自身情况的预测能力，本文研究就该场景建立TCN 预测模型，项目实验情景模拟如图2 所示。模型输出层输出为当前车下一帧在x 及y 轴上的坐标(x, y)，模型的输入为该时刻当前车的x，y 坐标、速度、加速度，被跟驰车的x，y 坐标、速度、加速度，共8 项参数。输入层的历史数据seq_len 定义为80，对应实际的8 秒时间。

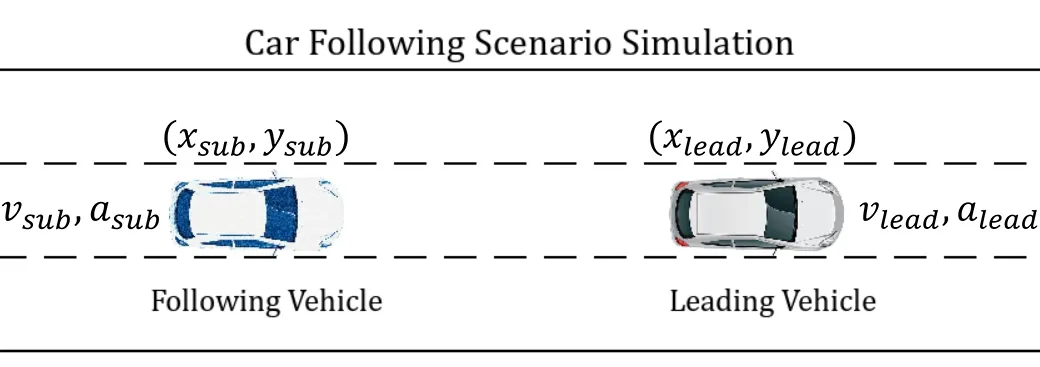
图2： 车辆跟驰场景模拟

3.2 数据准备

TCN 模型作为一种深度学习算法，需要训练包含一段较长时间的车辆跟驰行为的大量数据。因此，我们采用NGSIM 中的i-80 路段的数据集来训练集成模型。其轨迹数据是2005 年4 月13 日在加州埃默里维尔的旧金山湾区i-80公路东行处获得的。调查区域长约500 米（1640 英尺），行车方向由南向北，平均流量为7124 veh/h, 平均车速为8.32 m/s,由6 条高速公路车道组成，其中包括最右侧的一条集散车道，为典型的交通拥堵状态，因此我们选取该路段数据进行分析。考虑到最左侧车道存在频繁变道等现象，数据集中Lane_id 在2 到5 之间的中间车道被用于训练网络模型。对于每辆车来说，我们提取了与该车辆在同一车道，相距100m 内（因为常用传感器如LIDAR 或RADAR 的距离为60-175 米）最近的前车数据，其中两车应保持至少持续80 帧、间距不长于100m 的不变道跟驰行为。对于跟驰时间长于80 帧的数据，我们截取了其中前80 帧数据并每隔10帧再次截取80 帧数据作为新的一段跟驰行为数据。最终我们得到了192307 段汽车跟驰事件，其中3/4 的数据用于训练模型，1/4 的数据用于测试模型。

3.3 网络参数

与其他深度学习的网络模型类似，在TCN 模型中，许多参数都会影响模型的性能。对于单一网络在该跟车场景下最优参数的寻找，我们通过执行多组对照实验，改动不同组实验中的单一变量，寻找最优参数。对于每一个模型，我们在该场景下进行了多组实验模拟，通过比较最终预测结果准确性的方式给出各模型在该场景下的最优参数，并尽量保证不同网络非核心参数的一致性。以TCN 网络为例，我们通过调整卷积核大小k_nize，隐藏层数量level，隐藏层中神经元数量n_hid 和数据训练参数更新周期epoch，寻找神经网络收敛速度、最终模型预测效果等综合最优的一组参数，作为TCN 网络的最优参数，用于其与其他网络模型进行比较。如表1 所示。

根据不同参数下多轮数据训练及测试，当k_nize 为4，level 为4，n_hid 为32，epoch 为10 时，网络模型具有最小的均方误差(MSE)，在后续的训练中，我们使用该参数作为TCN 网络模型的参数，除此之外，根据车辆跟驰的实际情况及数据集特点，我们确立了TCN 网络模型的各项参数（表2）。

表2： TCN 网络各项参数

3.4 研究结果

3.4.1 预测准确率与收敛速度

我们取用了i-80 路段的跟车对标签集，将80 帧作为时间步长，实验比较了各网络在该时间步长的模型大小下经过一定轮数的训练达到的最优预测能力。以前80 个连续时间单位的前车与后车的x 与y 坐标、加速度与速度这个八个维度作为输入，以第81 时间点的后车位置坐标作为输出，对模型进行训练，并使用mse 损失函数对训练得到的网络的预测效果进行评价，得到各网络在相同测试数据集下的loss，如（表3），并在测试数据集中随机选取了200 个测试数据进行预测并绘制预测曲线图，结果如（图3）。可以看到，与其他网络模型相比，TCN 网络的预测结果更接近真实数据。我们记录了网络训练过程中的loss 值，并绘制曲线比较网络收敛速率（图3），可以看到，TCN 在1 ～2 轮训练后已经有较低的loss 了，而其他网络还需要重复训练几遍才能达到相对不错的效果。

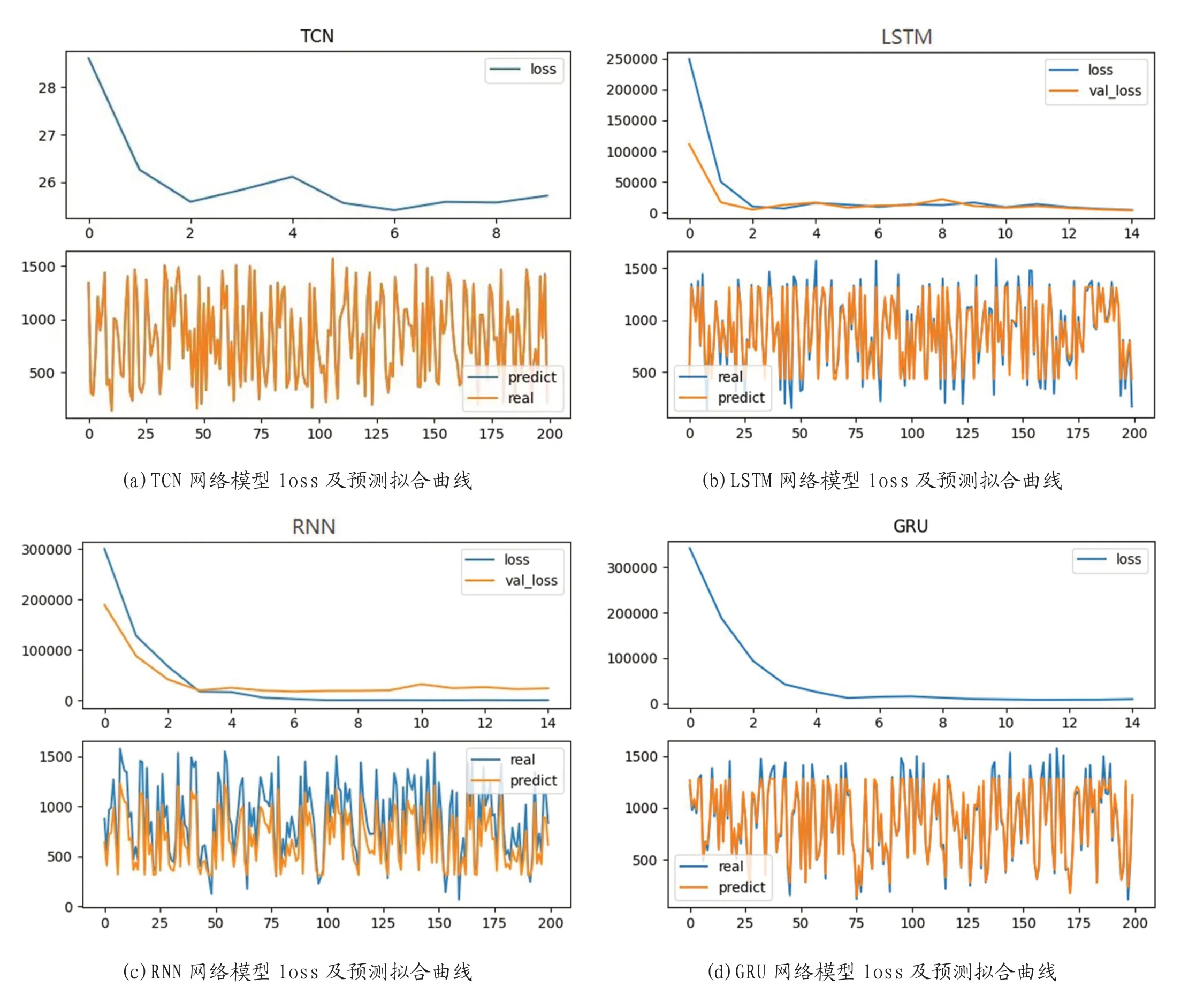
图3： 各网络模型loss 曲线与预测曲线

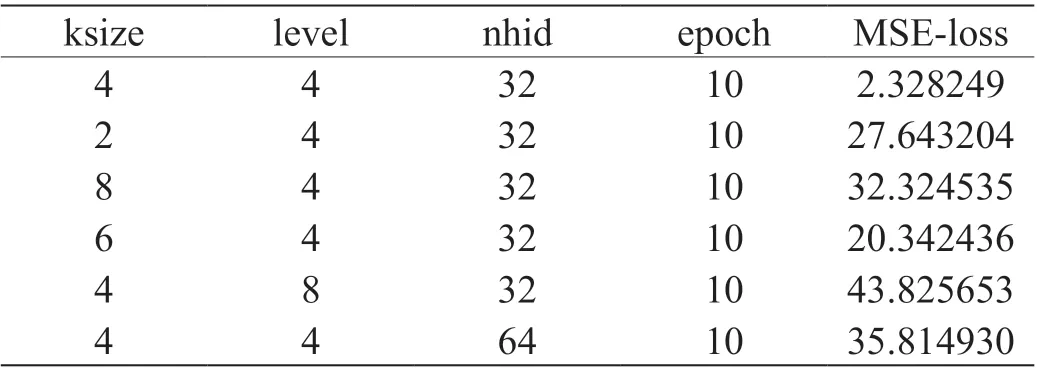
表 1：TCN 网络参数效率对比

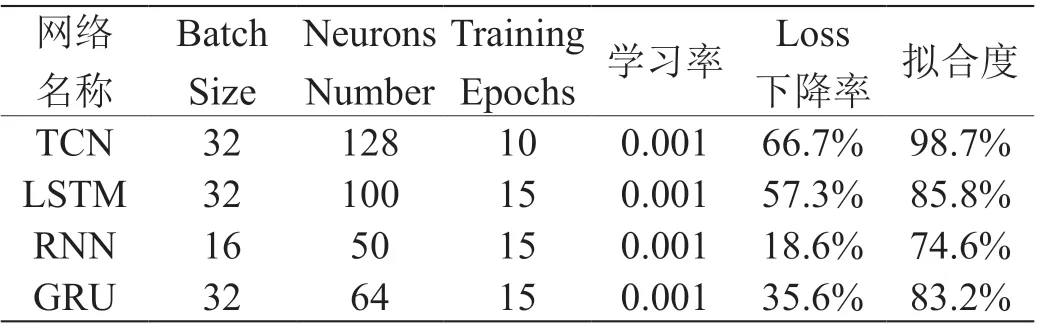
表 3：时序网络模型效率对比

3.4.2 泛化能力

HighD 数据集是德国高速公路的大型自然车辆轨迹数据集。我们将数据训练得到的网络预测NGSIM 数据集中us-101 路段、HighD 数据集中01_highway 路段的车辆跟驰行为，以考察各个网络的泛化能力。我们在测试数据集中随机选取了符合条件的50 个测试用例，用实验训练完成的各网络模型预测其跟驰行为，比较loss 大小，并绘制曲线比较预测结果（图4）。可以看到，各网络模型在us-101 路段、01_highway 路段下均具有较高的车辆行为还原度。其中， TCN网络模型对于数据的预测最接近真实值，具有最好的车辆行为还原度。该实验说明了与其他网络模型相比，TCN 具有较好的泛化能力且其泛化能力优于其他模型。

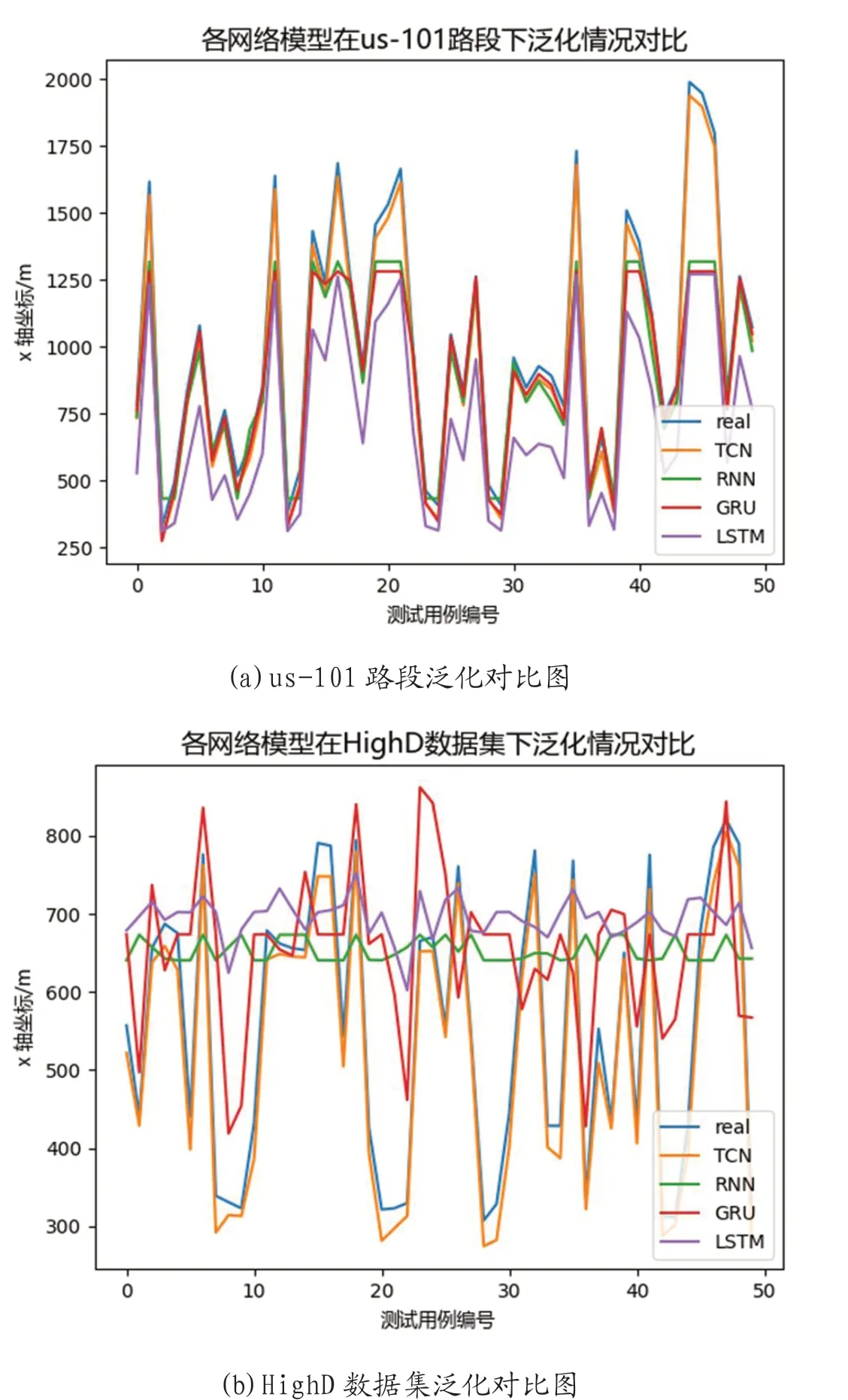
图4： 各网络模型泛化能力对比图

4 结论

作为主流的自动驾驶理论研究场景和典型的时间序列问题，跟驰模型的优化具有重要意义。本文将TCN 引入跟驰模型的研究，将卷积网络引入自动驾驶汽车车辆轨迹模型优化的研究，并通过实验证明了其可应用性及相对较高的准确性和稳定性，为上述问题的研究提供了新思路、新方法，相信时序卷积网络模型会在自动驾驶研究领域大放异彩。