初等数论知识在小学数学中的渗透
2022-07-08李凤清
赵 艳,李凤清
(1.蓬溪县实验小学,四川 蓬溪 629100;2.四川职业技术学院 教师教育学院,四川 遂宁 629000)
初等数论主要研究整数的性质与规律,与小学数学知识有着密切的联系。初等数论知识中的整数、整除、数的整除特征、素数、最大公因数、最小公倍数等知识既让学生增强对整数性质的了解,又为分数等知识的进一步学习奠基,还增强学生对数学史以及数论方面的数学家的了解,培育数学文化,激发学生的学习兴趣。如何以小学数学教材中“数的整除”一章中所展现知识内容为主导,找点发挥延伸,训练学生解决问题的能力,渗透初等数论的初步知识与思想方法,下面我们从几个方面以案例说明。
一、突出整数以及整除特性,结合一些运算性质解决问题
初等数论是研究整数的性质与规律,而小学数学中,有很多的整数问题,如人的个数、鸡的只数、分数的分子分母等皆为整数,突出整数特性,以及整除的概念。合理结合相关数学知识来解决问题,可以培养学生正确认识整数问题,提高解决整数问题的能力。
案例1在下面的括号里填上最简分数,使下面式子成立。


案例3 将数1,2,3,4,5,6,7,8,9 这九个数分别填在九宫格的九个格中,使每行、每列、两条对角线上三个数的和都相等。

分析:因为每行三个数之和相等,那么三行九个数之和就等于1,2,3,4,5,6,7,8,9 之和45,那么每行之和就为45÷3 = 15,故每列三个数之和与对角线三个数之和均为15。
由于第二行、第二列、主对角线、次对角线之12 个数之和就为15×4 = 60,这12 个数至少包含1,2,3,4,5,6,7,8,9,而1,2,3,4,5,6,7,8,9 之和为45,还多出60 - 45 = 15,显然是由于最中间格多算了3 次,故中间格填的数为15÷3 = 5。
1,2,3,4,5,6,7,8,9 这九个数中,其和等于15的三个数中若包含1,只有1,5,9 与1,6,8 两种情形,故1 只能填边不能填角,则可以填出:
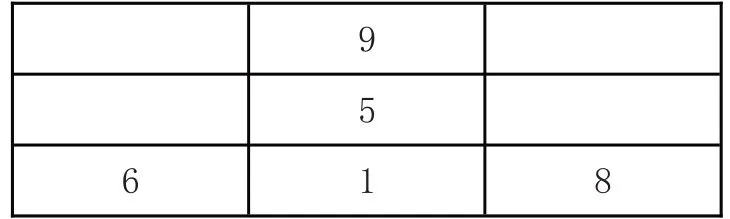
由此运用(行、列、对角线)三个数之和为15即可以填出其余四个格中的数。
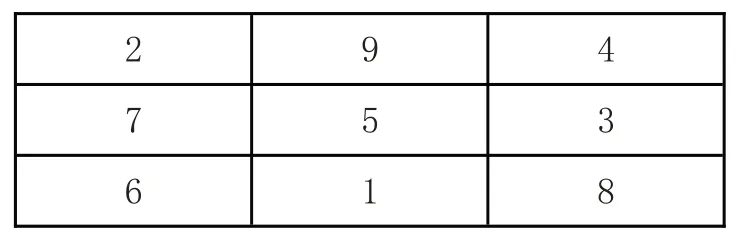
上面表格常被称为河洛图,又叫“河图洛书”,是关于中国古代文明的著名传说。六七千年前,龙马跃出黄河,身负河图;神龟浮出洛水,背呈洛书。伏羲根据河图洛书绘制了八卦。之后大禹治水,河伯献河图,宓妃献洛书,使得大禹终于战胜洪水[1-3]。
案例3 运用整数的运算特性,抓住中间格这个关键与1 的位置,顺利解决了问题,还对学生渗透中华传统文化。
案例4法国数学家费马发现F0= 220+ 1 = 3,F1= 221+ 1 = 5,F2= 222+ 1 = 17,F3= 223+ 1 =257,F4= 224+ 1 = 65537 都是素数,因为第5 个数F5= 225+ 1 = 232+ 1 实在太大了,费马认为这个数还是素数,于是在1640 年提出了以下猜想:形如Fn= 22n+ 1 的数都是素数。后来人们就把形如22n+ 1 的数叫费马数,很多人甚至将22n+ 1 称为素数公式。大约过了92 年,即1732 年,伟大的数学家欧拉算出F5= 641×6700417,也就是说F5不是素数,宣布了费马的这个猜想不成立,它不能作为一个求质数的公式,让人们在寻求素数公式的追求中受到一次沉重地打击。
其实,我们知道
216= 211×25= 2048×32 =(641×3 + 125)×32 = 641×96 + 4000 = 641×102 + 154,那 么216除 以641 余154,那么232除以641 就 与1542除以641 的余数相同,由于1542= 23716,而23716 除以641 余640,故232除以641 就余640,故232+ 1 就能被641 整除,故F5是一个合数,不是素数。
二、明确数的整除特征,渗透初等数论中同余的思想
运用整数的奇偶特征与性质,如奇数不等于偶数,奇数个奇数的和为奇数,偶数个奇数的和为偶数等等来解决一些问题,就可以转繁为简,突出本质。
案例536 口缸,九只船来装,装单不装双,试试怎么装?
该题中,九个奇数的和为奇数,而36 为偶数,由于奇数不等于偶数,因此不存在符合条件的方案。(民间把36 口缸偷换成三石六口缸而成为有解题目)
案例6某次展览为一个5×5 的方形展区,含一个门厅与24 个展室,如下图,每相邻两个展室均有门可通,参观者须从门厅开始到各展室观看展览,之后从门厅出去。请问是否存在一条路径,不重复不遗漏地观看完24 个展室。
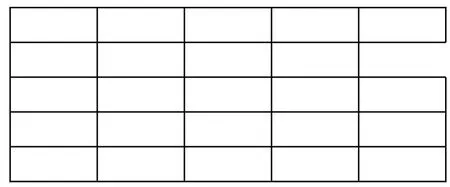
分析 我们将24 个展室标记为奇展室与偶展室两类,如下图:

那么参观者只能从奇展室到偶展室,或者从偶展室到奇展室,其路线必然是:
奇→偶→奇→偶→奇→偶…,则应该12 个奇与12 个偶,而图中有13 个奇,11 个偶,故这样的路径是不存在的。
我们运用奇偶分类,巧妙解决问题,对培养学生思维的深刻性很有帮助。
学生理解能被2、5 整除的数的特征,我们还要讲清道理,是任何一个整数N总可以分解成若干个10 加上个位数,即N= 10a+b,由于10a能被2、5 整除,那么当个位能被2、5 整除时,当然N就能被2、5 整除。
我们可以将上面这个知识点延伸[4],得到:
N除以2(或5)余几,关键看N的个位,个位上的数除以2(或5)余几,那么N除以2(或5)就余几。
继续延伸:
N除以4(或25)余几,关键看N的后两位,后两位上的数除以4(或25)余几,那么N除以4(或25)就余几。
N除以8(或125)余几,关键看N的后三位,后三位上的数除以8(或125)余几,那么N除以8(或125)就余几。
(我们可以把这类性质称为整除特征的响尾蛇特性)
大家知道9,99,999,9999,…,能被3(或9)整除,把这些数加上1,再除以3(或9)就该余1,因此10,100,1000,10000,…,等数除以3(或9)就该余1,那么我们就知道最高位是a,后面各位均为0 的整数除以3(或9)就该余a,如423 除以9 就转化为400 + 20 + 3 除以9,400 除以9 余数就为4,20 除以9 就余2,3 除以9 就余3,故423 除以9 的余数就为4 + 2 + 3,即能被9 整除。
案例7将1,2,3,…,9 这九个数字分别填进下面九个空中,使等式成立。

将符合条件的所填三个三位数相加,即□□□+□□□+□□□,易知这可拆分成(□+□+□)×100+(□+□+□)×10+(□+□+□),可知它除以9 后的余数与(□+□+□)×1+(□+□+□)×1+(□+□+□)除以9 的余数相同,而(□+□+□)×1+(□+□+□)×1+(□+□+□)等于1+2+3+4+5+6+7+8+9=45,能够被9 整除,可见□□□+□□□+□□□能被9 整除,而□□□+□□□+□□□为和□□□的两倍,它能被9 整除,那么和□□□能被9 整除(易知和这个三位数□□□的百十个三个位置上的数加起来为18。)。
例如,取和为918,则□□□+□□□=918,即可迅速填出243+675=918,645+273=918 等答案。依此方法我们可以得出所有的正确答案。
同余是初等数论中的重要概念,利用同余的思想方法来解决问题常常事倍功半。
设a为一位数,由于1、100、10000、1000000 这样 的 数 除 以11 均 余1,那 么a,a×100,a×10000,a×1000000,…这样的数除以11 的余数为a;设b为一位数,由于10、1000、100000、10000000这 样 的 数 除 以11 均 余10,那 么b×10,b×1000,b×100000,b×10000000,… 这样的数除以11 的余数为10b,总体特征为:一个整数去掉末尾偶数个零,除以11 后的余数不变。如求239674 除以11 余多少,就是(200000 + 30000 + 9000 +600 + 70 + 4)÷11 余多少,那么就等价于(20 +3+ 90 + 6 + 70 + 4)÷11 余多少,就是193÷11 余多少,即得余数为6。
还可以给小学生介绍1001 这个有趣的数,《一千零一夜》是1001 个美丽的童话,可以七个为一组,也可以十一个为一组,也可以十三个为一组,也就是1001 = 7×11×13,说明1001 可以被7或11 或13 整除,我们把六位数239674 分解为239×1000 + 674,再将它转化为与1001 有关系的式 子 239×1001 + 674 - 239 = 239×1001 + 435,故:
239674÷11 的余数与435÷11 的余数相同;
239674÷7 的余数与435÷7 的余数相同;
239674÷13 的余数与435÷13 的余数相同;
这样就把一个六位数求余数的问题转化为三位数求余数问题,化繁为简,解决问题。
按西方人的三位分节标注多位整数,如将123789668 这个数标注为123,789,668,这样就可以得到三个三位数123,789,668,由于123000000=123000×1001-123000,即可变形为123000×1001-123×1001+123,故123000000 除以7 或11 或13 的余数与123 除以7 或11 或13 的余数相同,由上可知789668 除 以7 或11 或13 与668-789 除 以7 或11或13 的 余数相同,故123789668 除 以7 或11 或13的余数就与123-789+668 除以7 或11 或13 的余数相同,即余数为2。
并且我们还可以进一步总结出下面结论:
一个多位数N按三位分节,把最末一节的三位数记为N1,倒数第二节的三位数为N2,倒数第三节的三位数为N3,…,那么N除以7 或11 或13与N1-N2+N3-N4+ …除以7 或11 或13 的余 数相同。
三、发掘教材内容,渗透两个数的最大公约数、最小公倍数的简单性质
教材中求两个数的最大公约数与最小公倍数使用的是短除法,把它模式化为下图:
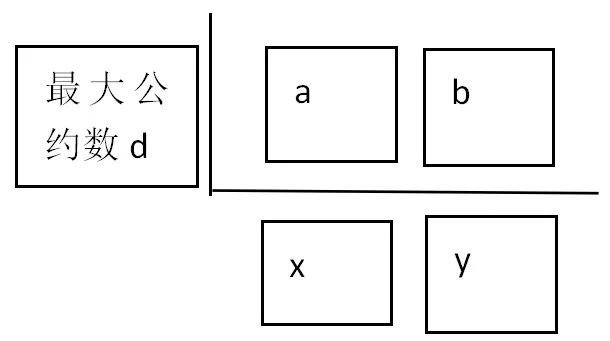
可知x,y互质,最小公倍数为dxy,a=dx,b=dy。即可得出结论[5]:两数的最大公约数与最小公倍数的乘积等于两数乘积。
案例8两个数的积是1260,它们的最大公约数是6,求这两个数。
从上面学生非常熟悉的短除法可以看出,这两个数的最大公约数为6 时,必满足x,y互质,那么这两个数分别为6x,6y,最小公倍数为6xy,那么乘积为36xy= 1260,即可知xy= 35,即可知x=1,y= 35 或者x= 5,y= 7。即得两数为6 与210 或者为30 与42。
案例9两个数的最大公约数为10,它们的最小公倍数为420,求这两个数。
由上面短除法可知两个数分别为10x,10y,最小公倍数为10xy,则10xy= 420,即可知xy= 42,由于x,y互质,即可知x= 1,y= 42 或者x= 2,y=21 或者x= 3,y= 14 或者x= 6,y= 7。即得两数为10 与420,或者为20 与210,或者为30 与140,或者为60 与70。
四、渗透整数标准分解思想,化整为零解决问题
向学生说明,由于素数不可再分解出比它小的质因数,故大于1 的整数都可以分解成素数的乘积,即可以写成2()3()5()7()…p()的形式[5]。我们先研究其局部2()、3()、…、p()的一些性质,再结合初等数论初步知识研究这些局部性质与整体性质的联系,渗透整数标准分解思想,化整为零解决问题[6]。
案例101000 的约数有多少个?所有约数的和是多少?
常规解法为先写出1000 的所有约数。我们可以让学生进一步了解一个事实,若b是a的约数,那么b的质因数必然是a的质因数。我们将1000 分解质因数为23×53,那么1000 的约数分解质因数就必然表示为2()5()的形式。23有1,2,4,8 四个约数,53有1,5,25,125 四个约数,23的任何一个约数与53的任何一个约数相乘都是1000 的约数,那么就有下面结论:23的约数个数4 与53的约数个数4 相乘就得到1000 的约数个数,即16,23所有约数的和15 与53的所有约数的和156 相乘就是1000 的所有约数的和2340。
对于这类问题,通过对1000 的标准分解23×53,转化为求23的约数个数、约数和与53的约数个数、约数和的问题,先化整为零,再从局部结果得出整体结果,且体现基本元素思想。
五、适度拓宽素数的相关知识,渗透初等数论方面的数学文化
向学生介绍素数的知识的同时,适度介绍素数研究的历史与现状,介绍我国在数论研究方面的数学家,如华罗庚、陈景润等,还要抓出一些案例,使学生了解素数的分布、筛法等初步知识。
案例11 介绍孪生素数的概念与研究现状(孪生素数是否有无数多对,现在发现的最大的孪生素数等)。如5 与7,11 与13,17 与19 等就是孪生素数,问题:大于3 的两个孪生素数的乘积加上1 后一定是()的倍数。
知识点:除2 与3 之外的素数都紧挨在6 的倍数前或后(为什么?6n- 2,6n+ 2 是偶数,6n+ 3是3 的倍数),则孪生素数总在某一个6 的倍数前与后,这两个数就可以表示为6n- 1,6n+ 1,由于(6n- 1)(6n+ 1)+ 1 = 36n2,即可知填36。
拓展:p为大于3 的素数,那么p2- 1 一定是()的倍数,为什么?
上面是我们对小学生渗透初等数论知识的一点做法。我们从多年的教学感受认识到,紧贴教材,适度发挥,不仅能开发学生的智力,增强数学核心素养,还能发现一些有数学天赋的孩子。
