基于气动参数辨识的变体飞行器自适应控制方法
2022-07-08曹承钰廖宇新曹玉腾
曹承钰,廖宇新,曹玉腾,李 珺
(1.中南大学 航空航天学院,湖南 长沙 410083;2.北京航天自动控制研究所,北京 100854)
0 引言
为进一步改善飞行器的气动性能并提高飞行器的环境适应能力,变构型的思想应运而生。对于可变构型的变体飞行器而言,其姿态控制往往具有多变量、快时变、强耦合、强非线性、不确定性等特点,且上述特征会因变形引起的气动力与气动力矩、质心、压心和转动惯量等参数的改变而更加显著。此外,在变体飞行器飞行过程中,其气动参数的变化通常无法被精确预知或测量[1]。因此对变体飞行器气动参数进行在线辨识,并基于辨识结果设计高精度、强适应性的姿态控制方法具有重要意义。
目前常用的气动参数辨识方法有最小二乘法[2]、极大似然法[3]、Kalman滤波算法[4]以及智能算法[5]等。最小二乘法因有偏估计的特点,精度往往难以满足要求。极大似然法虽然能获得较高的辨识精度,但迭代计算耗时较长,难以满足在线辨识的时效性要求。智能算法辨识精度高且具备全局寻优能力,但收敛速度较慢,对计算能力要求高,在线应用难度大。扩展卡尔曼滤波(extended Kalman filter,EKF)算法将非线性模型进行一阶近似,进而对系统状态进行递推估计,在求解非线性状态实时估计问题中体现出良好的性能[6]。文献[4]提出了一种基于EKF算法的气动参数辨识方法,实现了滤除噪声和对未知气动参数的精确估计。本文将基于EKF算法设计气动参数辨识方法,在有限的计算资源消耗下实现较高精度的气动参数在线辨识。
滑模控制(sliding mode control,SMC)因其在抗干扰能力上的优势,已被广泛应用于变体飞行器姿态控制中[7]。文献[8]针对伸缩翼变形飞机,采用SMC方法设计了姿态跟踪控制器,并通过仿真验证了控制器的鲁棒性。此外,结合基于观测器的干扰估计与补偿技术,可进一步提高控制器的抗干扰能力。文献[9]提出了一种基于SMC方法的切换抗扰姿态控制方法,其结合干扰观测器对耦合多源不确定性的精确估计,实现了临近空间变体飞行器的高精度鲁棒姿态控制。上述抗干扰策略在飞行器模型参数存在较大不确定性时具有一定局限性,为确保良好的控制效果,有必要对存在较大不确定性的气动参数进行在线辨识,并将辨识结果用于控制器中的模型参数更新。
本文针对考虑气动参数不确定性和外部干扰的变体飞行器姿态控制问题开展研究,提出了一种基于气动参数在线辨识的自适应控制方法。其首先基于变体飞行器运动模型,建立了气动参数辨识模型和面向控制的模型;然后,基于扩展卡尔曼滤波算法,设计了一种气动参数辨识方法以实现对未知气动参数的在线辨识,并进一步结合辨识所得气动参数与基于SMC和干扰观测器的控制方案,提出了一种自适应控制方法;最后,通过数值仿真验证了所提出方法的有效性。
1 数学模型及问题描述
1.1 变体飞行器运动模型



1.2 气动参数辨识模型
变体飞行器气动参数辨识模型主要包括状态方程和量测方程两部分。
(1)状态方程
本文主要关注变体飞行器姿态控制,在气动参数辨识过程中,主要辨识相关气动力矩参数,待辨识量为式(6)中的cmi(*)项。因此,状态方程可只考虑绕质心运动方程,如式(2)所示。
(2)量测方程
本文主要基于过载、角速率和由惯组数据解算得到的姿态角信息,建立辨识所需的量测模型。量测模型的形式如下:

式中:γ——滚转角;ψ——偏航角;φ——俯仰角;Nx,Ny,Nz——轴向过载、法向过载和横向过载;m——量测量对应的量测值;χ(*)——相应的量测噪声;TBG(i,j)——转换矩阵TBG的第i行第j列元素。
1.3 面向控制的模型及问题描述

2 基于气动参数在线辨识的自适应控制方法
2.1 基于EKF的气动参数在线辨识方法
2.1.1 气动参数在线辨识方法



2.1.2 气动参数可辨识性分析

2.2 自适应控制方法
2.2.1 多变量干扰观测器



在控制器[式(33)]中,可通过调整kp项,保证系统的指数级收敛速度;通过调整幂次项γp,确保在快速趋近的同时削弱抖振;根据扰动上界调整Ep项,以保证系统的鲁棒性。
基于气动参数在线辨识的变体飞行器姿态控制原理如图1所示。在系统[式(8)]存在不确定气动参数cmi(*)和总扰动d1的情况下,采用所提出的基于EKF的气动参数在线辨识方法实时辨识cmi(*),并将辨识结果用于控制器[式(33)]参数的更新;进一步,基于MDO对总扰动d1的精确估计及其在控制器中的补偿作用,实现对期望姿态指令X1d的高精度、强适应性跟踪。

图1 变体飞行器姿态控制框图Fig.1 Flowchart of attitude adaptive control of morphing vehicle
3 仿真结果与分析
本仿真主要分为两部分,分别为气动参数在线辨识仿真和基于气动参数在线辨识的自适应控制仿真,具体仿真时序如下:0~30 s为气动参数在线辨识仿真;30~50 s为基于气动参数在线辨识的自适应控制仿真。
3.1 气动参数在线辨识仿真



表1 待辨识参数敏感度指标值Tab.1 Sensitivity index values of parameters to be identified
采用3-2-1-1方波作为激励输入信号,直接叠加于姿态角和折叠角期望指令上。激励信号的数学模型为
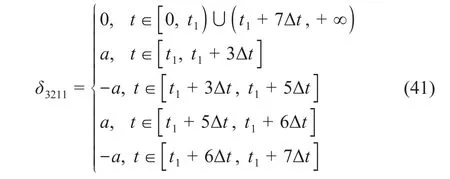
式中:a——单方波幅值;Δt——单方波作用时长;t1——激励信号作用的初始时刻。
图2和图3分别给出了仿真过程中姿态角跟踪曲线和折叠角指令信号曲线,图4和图5分别给出了姿态角和姿态角速度在闭环辨识过程中的估计曲线。由仿真结果可知,无论是姿态角还是姿态角速度,均具有较高的估计精度。其中,攻角和倾侧角估计误差均在[-0.02°,0.02°],侧滑角估计误差在[-0.05°,0.05°]。

图2 姿态角跟踪曲线及姿态角激励信号Fig.2 Tracking curves of attitude angle and attitude excitation signal
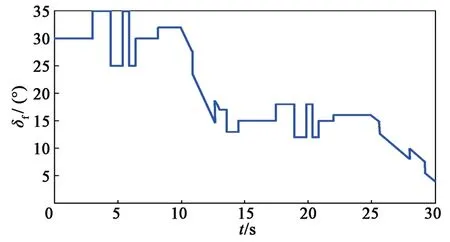
图3 折叠角指令信号及激励信号Fig.3 Command signal and excitation signal of folding angle

图4 姿态角估计曲线Fig.4 Estimation curves of attitude angle
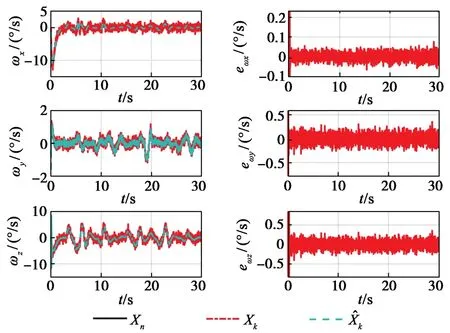
图5 姿态角速度估计曲线Fig.5 Estimation curves of attitude angular velocity
气动参数辨识结果如表2所示。以ηc为例,图6给出了参数辨识过程中气动参数相对误差的变化曲线。由此可见,气动参数辨识值精度较高。在已辨识的气动参数中,所有气动参数相对误差均小于10%,且90%以上的气动参数相对误差小于5%,50%以上的参数辨识误差小于1%。总之,俯仰通道的气动参数辨识精度高于滚转通道和偏航通道。

图6 ηc的辨识曲线Fig.6 Identification curves ofηc
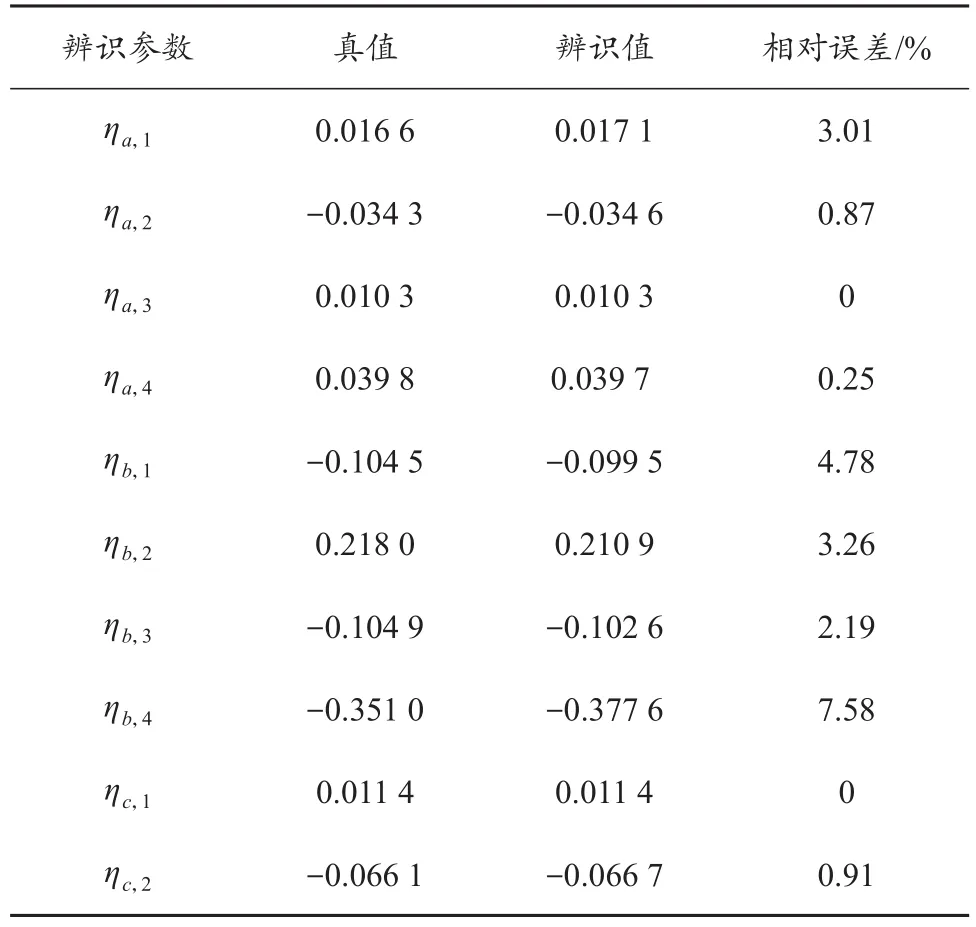
表2 气动参数辨识结果Tab.2 Identification results of aerodynamic parameters
3.2 自适应控制仿真
在本部分仿真中,通过参数拉偏模拟气动参数不确定性,即假设上述待辨识参数均存在20%~25%的随机偏差。为检验本文所提控制方法的有效性,进行4种不同方法下的跟踪效果对比仿真:
(1)方法1,即本文提出的自适应控制方法;
(2)方法2,即基于干扰观测器的滑模控制方法(SMC*),该方法不进行气动参数在线辨识,有干扰观测器;
(3)方法3,即滑模控制方法(SMC),该方法既不进行气动参数辨识,也无干扰观测器;
(4)方法4,即基于干扰观测器的动态面控制方法(DSC),控制器形式如文献[13]所示,该方法不进行气动参数在线辨识,有干扰观测器。
仿真中,干扰观测器形式如式(30)所示,滑模控制器形式如式(41)所示。
图7、图8分别给出了4种不同方法下的姿态角跟踪曲线和姿态角误差曲线,图9给出了姿态角速度曲线。由仿真结果可知,本文提出的控制方法(即方法1)能实现最高的跟踪精度;方法2和方法4的次之,且方法2的优于方法4的;方法3精度最低。综合来看,干扰观测器对干扰及参数不确定性的估计与补偿作用往往是有限的,因此有必要在现有可测数据的基础上,进行气动参数的在线辨识,从而进一步提高控制器对干扰及不确定性的适应能力。

图7 姿态角跟踪曲线Fig.7 Tracking curves of attitude angle
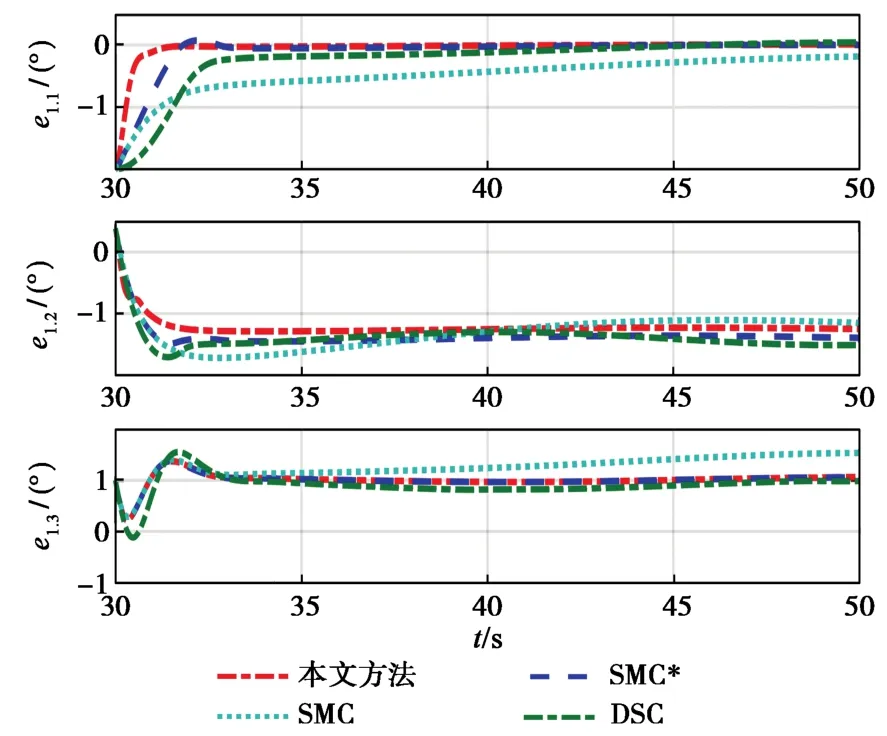
图8 姿态角跟踪误差曲线Fig.8 Curves of attitude angle tracking error

图9 姿态角速度曲线Fig.9 Curves of attitude angular velocity
4 结语
本文研究了气动参数不确定性和外部干扰影响下的变体飞行器姿态控制问题,提出了一种基于气动参数在线辨识的自适应控制方法。首先,建立了变体飞行器气动参数辨识模型和面向控制的模型;然后,基于EKF算法设计了气动参数在线辨识方法,并提出了基于滑模控制和干扰观测器的控制方案,其中,在线辨识结果将用于控制器中的模型参数更新,以实现变体飞行器自适应姿态控制;最后,进行了气动参数在线辨识仿真和自适应控制仿真。仿真结果表明,本文所提出的气动参数在线辨识方法具备较高的参数辨识精度,且在自适应控制对比仿真中实现了最高的跟踪精度。综合来看,相比于仅采用SMC或观测器的抗干扰控制方法,本文提出的自适应控制方法以高精度气动参数辨识结果作为控制器高可靠模型基础,同时充分利用SMC和干扰观测器在抗扰动能力上的优势,可有效提高变体飞行器在外部干扰和较大气动参数不确定性影响下的姿态控制精度和控制器的适应性及鲁棒性。实际中,飞行器可实时在线获得的量测信息是有限的,且量测精度均有不同限制。本文所采用的基于扩展卡尔曼滤波算法的气动参数辨识方法对量测精度要求较高,因此,如何降低滤波算法对量测量及量测精度的依赖性是后续需要着重考虑的问题。
