术语研究中的最小编辑距离

冯志伟 周建 于洋

摘 要：最小编辑距离是比较语言中不同符号串之间相似程度的一种方法，这种方法计算不同符号串之间转换时的删除、插入、替代等运算的操作数，通过动态规划算法进行算法描述。在术语研究中，可以使用最小编辑距离对术语特征进行定量化计算。在计算语言学中，可以使用最小编辑距离发现潜在的拼写错误，进行错拼更正。在语音识别中，可以使用最小编辑距离计算单词的错误率。在机器翻译中，可以使用最小编辑距离进行双语语料库的单词对齐。

关键词： 最小编辑距离;动态规划算法;术语对齐;字符串相似程度

中图分类号：H083; N04  文献标识码：A  DOI：10.12339/j.issn.1673-8578.2022.03.001

Minimum Editing Distance in Term Research //FENG Zhiwei， ZHOU Jian， YU Yang

Abstract： Minimum editing distance is a method for comparing the degree of similarity between different symbol strings in a language. This method calculates the number of operations such as deletion， insertion， substitution in transforming between different symbol strings， and can be described algorithmically by a dynamic programming algorithm. In terminology， the minimum editing distance can be used to quantify the term features. In computational linguistics， the minimum editing distance can be used to find potential spelling errors and perform misspelling corrections. In speech recognition， minimum editing distance can be used to calculate the error rate of words. In machine translation， the minimum editing distance can be used for alignment of words in bilingual corpus.

Keywords： minimum edit distance; dynamic programming algorithm; term alignment; similarity between different symbol strings

收稿日期：2022-01-29  修回日期：2022-04-11

引言

语言研究中，常常需要比较不同符号串之间的相似程度。在自然语言处理中，不同的单词也是不同的符号串，组成这些不同符号串的字母有相同的部分，也有不同的部分，可以采用最小编辑距离（minimum edit distance）来描述这符号串之间的相似程度[1-2]。在术语研究中，术语也就是符号串，因此可以使用最小编辑距离对术语之间的相似程度进行数学描述。

1 最小编辑距离的原理

最小编辑距离就是把一个符号串转换为另一个符号串时所需要的最小编辑操作的次数。

例如，在进行符号串转换时，英语的intention（意图）和execution（执行）这两个符号串之间最小需要进行5个操作，它们之间的最小编辑距离就是5。

具体说明如下：把intention和execution这两个符号串之间的最小编辑距离表示为对齐（alignment）操作。如图1，I与空符号对齐，N与E对齐，T与X对齐，E与E对齐，空符号与C对齐，N与U 对齐，T与T对齐，I与I对齐，O与O 对齐，N与N对齐。在对齐的符号串下方的标记，说明从上面的符号串转换为下面的符号串要做的操作，符号的一个序列就表示一个操作表（operation list）。最下面一行给出了从上面的符号串到下面的符号串转换时的操作表：d表示删除（delete），s表示替代（substitute），i表示插入（insert）。I与空符号对齐时要把I删除，所以用d表示;N与E对齐时要用E来替代N，所以用s表示;T与X对齐时要用X来替代T，所以也用s表示;E与E对齐时，不进行任何操作;空符号与C对齐时要插入C，所以用i表示;N与U 对齐时要用U来替代N，所以用s表示;T与T对齐，I与I对齐，O与O 对齐，N与N对齐，都不进行任何操作。这样便得到intention和execution对齐时的操作表dssis，也就是“删除-替代-替代-插入-替代”。

也可以把intention和execution的对齐过程看作是从intention到execution转换过程，即：

第1步：删除 intention中的第一个字母i，得到ntention;

第2步：用e替代ntention中的第一個字母n，得到etention;

第3步：用x替代etention中的第二个字母t，得到exention;

第4步： 在exention中的第四个字母n和第五个字母t之间插入字母u，得到exenution;

第5步：用c替代exenution中的第四个字母n，得到execution。

转换过程如图2所示。从而得到从intention转换为execution时的操作表也是dssis。

可以赋给每个操作一个代价值（cost）或权值（weight）。1966年，Levenshtein（列文斯坦）建议，在上面的删除、替代和插入3种方法中，每一个操作的代价值都为1，而用同一个字母来替代它自己时代价值为0（例如，用字母T来替代字母T的代价值为0）[3]。两个序列之间的列文斯坦距离（Levenshtein distance）是最简单的加权因子，这个加权因子也就是最小编辑距离。所以，根据intention和execution对齐时的操作表dssis，这两个单词之间的列文斯坦距离为1+1+1+1+1=5，这意味着，这两个单词之间的最小编辑距离为5。

此外，Levenshtein还提出了另一种不同的度量方法。这种方法规定，插入或脱落操作的代价值为1，不容许替代操作[3]。不过，Levenshtein认为，也可以把替代操作表示为一个脱落操作加上一个插入操作，这样，替代操作的代价值应该为2，这实际上也就等于容许了替代操作。使用这样的度量方法，根据intention和execution对齐时的操作表dssis，这两个单词之间的列文斯坦距离应该是1+2+2+1+2=8，根据这样的度量方法，这两个单词之间的最小编辑距离为8。可以认为，Levenshtein取替代操作的代价值为2是合理的，因为一个替换操作，实际上相当于“先删除”和“后插入”两个操作。因此这样的度量方法是合理的，所以在本文中采用这样的方法进行度量。

2 最小编辑距离的动态规划算法

在自然语言的计算机自动处理中，最小编辑距离可以通过动态规划算法（dynamic programming algorithm）来进行算法描述[3]。

用序列比较的动态规划算法工作时，要建立一个编辑距离矩阵（edit distance matrix），目标序列的每一个符号按照自左而右的顺序记录于矩阵的行中，源序列的每一个符号按照自下而上的顺序记录在矩阵的列中，也就是说，目标序列的字母沿着底线自左而右排列，源序列的字母沿着侧线自下而上排列。对于最小编辑距离来说，这个矩阵就是编辑距离矩阵。每一个编辑距离单元[i， j]表示目标序列第i个字符和源序列的第j个字符之间的距离。每个单元可以作为周围单元的简单函数来计算。

计算每个单元的值的时候，取到达该单元时插入（ins）、替代（sub）、删除（del）3个可能路径中的最小路径为其值，计算公式如下：

distance[i-1， j] + ins-cost（target i-1）

distance[i，j] = mindistance[i-1， j-1] + sub-cost（source j-1， target i-1） distance[i， j-1] + del-cost（source j-1））

图3中的伪代码（pseudo code）对此最小编辑距离算法做了归纳。

图3中，各种代价值可以是固定的（例如x， ins-cost（x）=1），也可以针对个别字母做特别说明（例如，说明某些字母比另外一些字母更容易被替代）。假定相同的字母进行替代时，其代价值为0。

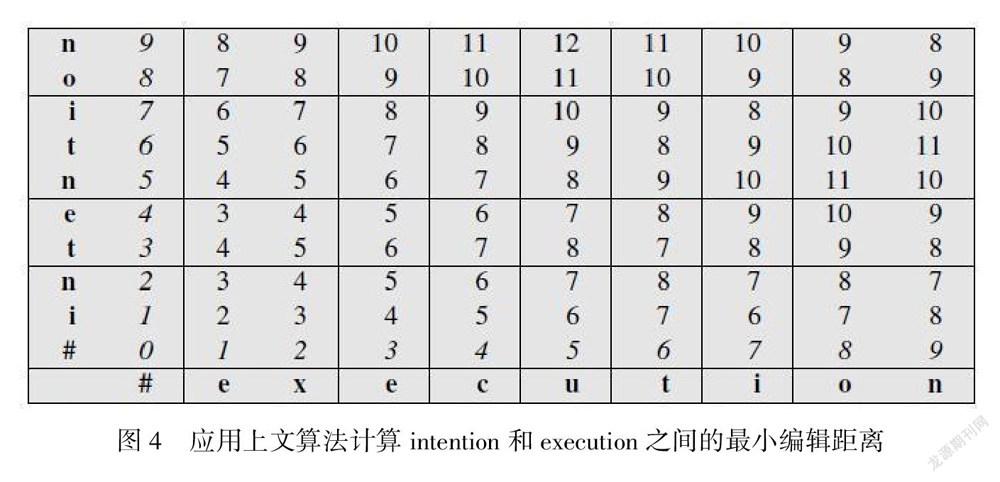
图4是应用最小编辑距离算法计算intention和execution之间距离的结果，计算时采用了Levenshtein提出的第二種度量方法：插入和删除的代价值分别取1，替代的代价值取2，当相同的字母进行替代时，其代价值为0。每一个单元都存在插入、脱落和替代3种可能性，最小编辑距离算法以这3种可能路径中的最小路径为其值。采用这样的计算方法，从矩阵的开始点出发，每一个单元都在插入、脱落和替代3种可能性之间进行选择，因此能够把矩阵中所有的单元都填满。如图4所示。

（计算时采用了Levenshtein距离;斜体字符表示从空符号串开始的距离的初始值，矩阵中的所有的单元都填满了。）

采用最小编辑距离算法，在图4中，首先要删除intention中的i，从第1列第0行开始计算。

图4中的一种可行的计算步骤如下：

——首先删除i，在第1列第0行，得1分，积累为1分;

——用e替换n，在第1列第2行，得2分，积累为1+2=3分;

——用x替换t，在第2列第3行，得2分，积累为3+2=5分;

——e不变，在第3列第4行，不得分，积累为5分;

——用c替换n，在第4列第5行，得2分，积累为5+2=7分;

——在c后插入u，在第5列第5行，得1分，积累为7+1=8分;

——t与t完全相同，在第6列第6行，不得分，积累为8+0=8分;

——i与i完全相同，在第7列第7行，不得分，积累为8+0=8分;

——o与o完全相同，在第8列第8行，不得分，积累为8+0=8分;

——n与n完全相同，在第9列第9行，不得分，积累为8+0=8分;

因此总积累为8分。

为了扩充最小编辑距离算法，使它能够进行对齐（alignment），可以把对齐看作是通过编辑距离矩阵的一条路径（path）。图5中使用带阴影的小方框来显示这条路径。路径中的每一个小方框表示两个符号串中的一对字母对齐的情况。如果两个这样带阴影的小方框连续地出现在同一个行中，那么，从源符号串到目标符号串就会有一个插入操作;如果两个这样带阴影的小方框连续地出现在同一个列中，那么，从源符号串到目标符号串就会有一个删除操作。

图5从直觉上说明了如何计算这种对齐路径。计算过程分为两步，分述如下：

（1） 第一步中，在每一个方框中存储一些指针来提升最小编辑距离算法的功能。方框中指针要说明当前的方框是从前面的哪一个（或哪些个）方框来的方向。图中分别标示出了这些指针的情况。在某些方框中出现若干个指针，这是因为在这些方框中最小的扩充可能来自前面的若干个不同的方框。指针“←”表示“插入”操作，指针“↓”表示“删除”操作，指针“”表示“替换”操作。

（2） 第二步中，进行追踪（back-trace）。追踪时从最后一个方框（处于最后一行与最后一列的方框）开始，沿着指针箭头所指的方向往后追踪，穿过这个动态规划矩阵。在最后的方框与初始的方框之间的每一个完整路径，就是一个最小编辑距离的对齐。

图5中，在每一个方框中输入一个值，并用箭头标出该方框中的值是来自与之相邻的3个方框中的哪一个方框，一个方框最多可以有3个箭头（“←”“↓”“”）。当这个表填满之后，使用追踪的方法来计算对齐结果（也就是最小编辑路径）。计算时，从右上角代价值为8的方框开始，顺着箭头所指的方向进行追踪。图5中灰黑色的方框序列表示在两个符号串之间可能的最小代价对齐的结果。根据灰黑色方框序列中的结果，计算最小编辑距离的值。首先要删除intention中的i，从第1列第0行开始计算，计算步骤如下：

——首先删除i，在第1列第0行，得1分，积累为1分;

——用e替换n，在第1列第2行，得2分，积累为1+2=3分;

——用x替换t，在第2列第3行，得2分，积累为3+2=5分;

——e不变，在第3列第4行，不得分，积累为5分;

——在e后插入c，在第4列第4行，得1分，积累为5+1=6分;

——用u替换n，在第5列第5行，得2分，积累为6+2=8分;

——t与t完全相同，在第6列第6行，不得分，积累为8+0=8分;

——i与i完全相同，在第7列第7行，不得分，积累为8+0=8分;

——o与o完全相同，在第8列第8行，不得分，积累为8+0=8分;

——n与n完全相同，在第9列第9行，不得分，积累为8+0=8分;

总积累仍然为8分。

因此，intention和execution之间的最小编辑距离为8。

3 最小编辑距离与术语研究

上文描述的最小编辑距离方法对于术语研究是有启发的。中文术语是用汉字来表示的，汉字也是一种符号，而术语就是由汉字构成的符号串，因此，可以使用最小编辑距离从数学上来衡量中文术语之间的接近程度，对中文术语进行定量化的描述。

例如，在计算机术语中，有“磁盘存储器（magnetic disc storage）、磁盘机（magnetic disc unit）、磁盘驱动器（magnetic disc drive）、磁头（magnetic head）、磁头加载区（magnetic head loading zone）”等中文术语，人们从感性层面觉得“磁盘机、磁盘驱动器、磁头、磁头加载区”与“磁盘存储器”的接近程度是不同的，“磁盘机、磁盘驱动器”与“磁盘存储器”比较接近，而“磁头、磁头加载区”与“磁盘存储器”相距较远。但是，这样的感觉终究是主观的，很可能因人而异。如果采用最小编辑距离，就可以对人们的主观感受进行定量化计算，使之得到精确的描述，从而避免认识的主观性。

上述术语的最小编辑距离分别计算如下：

磁盘存储器

磁盘机 * *

s d d

最小编辑距离 = 2+1+1 = 4

磁盘存储器

磁盘驱动器

s s

最小编辑距离 = 2+2 =4

磁盘存储器

磁头 * * *

s d d d

最小编辑距离 = 2+1+1+1 = 5

磁盘存储器

磁头加载区

s s s s

最小编辑距离 = 2+2+2+2 = 8

“磁盘机、磁盘驱动器”与“磁盘驱动器”的最小编辑距离为4，而“磁头、磁头加载区”与“磁盘存储器”的最小编辑距离分别为5和8。最小编辑距离的计算结果与人们的主观感觉是吻合的。这样，主观感受就获得了定量化的数学描述。

由此可见，如果使用最小编辑距离来计算不同术语之间的接近程度，能夠使人们对不同术语之间的接近程度的主观感受获得定量的认识。这是计算术语学（computational terminology）研究中一个值得关注的有趣问题[1]。

4 结语

最小编辑距离是比较不同符号串之间相似程度的数学方法，这种方法可以采用动态规划算法来进行算法描述。在术语学中，最小编辑距离可以用来对术语进行定量化的计算。在计算语言学中，最小编辑距离可以用来发现潜在的拼写错误，进行拼错更正。如果对于最小编辑距离做一些轻微改动，还可以用来做两个符号串之间的最小代价对齐。在语音识别中，可以使用最小编辑距离对齐来计算单词的错误率。在机器翻译中，因为双语并行语料库中的句子需要彼此匹配，使用最小编辑距离进行单词对齐也是非常有用的一种方法[4]。

参考文献

[1] 冯志伟.自然语言处理简明教程[M]. 上海：上海外语教育出版社，2020：75.

[2] WAGNNER R A， FISCHER M J. The string-to-string correction problem[J]. Journal of the Association for Computing Machinery， 1974， 21（1）： 168-173.

[3] LEVENSHTEIN V I. Binary codes capable of correcting detections， insertions， and reversals[J]. Soviet Physics Doklady， 1966， 10（8）：707-710.

[4] JURAFSKY D， MARTIN J H. Speech and Language Processing： An Introduction in Natural Language Processing， Computational Linguistics， and Speech Recognition[M]. 2nd ed. New York： Person Education Inc.， 2009：107-111.

作者简介：冯志伟（1939—），男，博士生导师，中国中文信息学会会士，中国人工智能学会理事，杭州师范大学外国语学院特聘教授，教育部语言文字应用研究所研究员。主要研究方向为计算语言学、计量语言学、理论语言学、语料库语言学、术语学等。出版中外文专著38部，发表中外文论文500多篇，主持编制国际标准1项和国家规范3项，参与编制国家标准14项，曾获中国计算机学会NLPCC杰出贡献奖、奥地利维斯特奖、香港圣弗兰西斯科技人文奖。通信方式：zwfengde2010@163.com。

周建（1979—），男，硕士，杭州师范大学外国语学院讲师。主要研究方向为专门用途英语教育（ESP）、语料库语言学和翻译技术等。通信方式：james@hznu.edu.cn。

于洋（1988—），男，博士，大连海事大学外国语学院讲师。主要研究方向为计量语言学、语料库语言学和词源学等。通信方式：yuyang89@dlmu.edu.cn。