平行泊车路径规划与跟踪控制仿真分析

覃立仁 张成涛 杨航 赵浙栋 谭泽旦

摘  要：随着汽车保有量的增多，泊车环境变得复杂，驾驶经验不足的驾驶员难以安全地完成平行泊车操作，泊车安全性问题成为研究热点。结合某款车型参数，针对平行泊车的路径规划和路径跟踪问题进行研究和分析。根据三阶贝塞尔曲线的性质，基于车辆运动学采用两段三阶贝塞尔曲线和倒推法规划出一条无碰撞的参考路径，利用模型预测控制进行路径跟踪，最后通过Simulink与Carsim进行联合仿真，得到的轨迹曲率连续且安全无碰撞，轨迹跟踪结果与参考轨迹基本吻合，验证了利用该方法进行平行泊车的路径规划与跟踪控制的可行性。

关键词：平行泊车;路径规划;路径跟踪;贝塞尔曲线;模型预测控制

中图分类号：U491.7           DOI：10.16375/j.cnki.cn45-1395/t.2022.03.003

0    引言

随着科学技术的发展和经济的增长，汽车逐渐成为重要的交通工具，给人们的出行带来了便利，但也造成了许多交通事故，其中由泊车引起的交通事故约占1/5。面对复杂的泊车环境，即使经验丰富的驾驶员也需要小心翼翼地反复调整才能将车辆安全地驶入车位。虽然现在很多汽车都安装倒车雷达、倒车影像等辅助泊车装置，但驾驶员的视野仍会受到一定的限制，对车辆周围的环境观察不到位，导致泊车过程中与其他车辆、行人等发生碰撞，造成经济损失或危及人们的生命安全。因此，研究者们对自动泊车系统开展研究，以期能有效解决泊车问题。

对于路径规划与跟踪问题，Kim等[1]采用两段圆弧添加一段直线的方式来规划泊车路径，这种方式虽然简单，但是得到的路径曲率不连续，增加了路径跟踪难度。Gómez-Bravo等[2]采用两段相切的圆弧的方式来规划泊车路径，基于模糊控制理论设计控制规则，但控制精度不高。Demirli等[3]采用多项式曲线和模糊控制网络来规划泊车路径，但该方法计算量较大。吴中伟等[4-6]采用B样条曲线进行路径规划设计，得到了曲率连续路径，但是参数较多，求解过程较为复杂。Moon等[7]运用逆向泊车的方式，用贝塞尔曲线和圆弧的方式得到了一条曲率连续的泊车路径，但利用两种线形规划来计算控制点的方式比较复杂。

本文基于贝塞尔曲线的性质采用倒推法进行轨迹规划，利用两段三阶贝塞尔曲线进行平行泊车参考轨迹规划，结合车辆和泊车位的约束条件，计算贝塞尔曲线各个控制点的坐标，规划出一条无碰撞的参考轨迹;结合车辆运动学模型，利用模型预测控制来实现轨迹跟踪。

1    车辆运动学建模

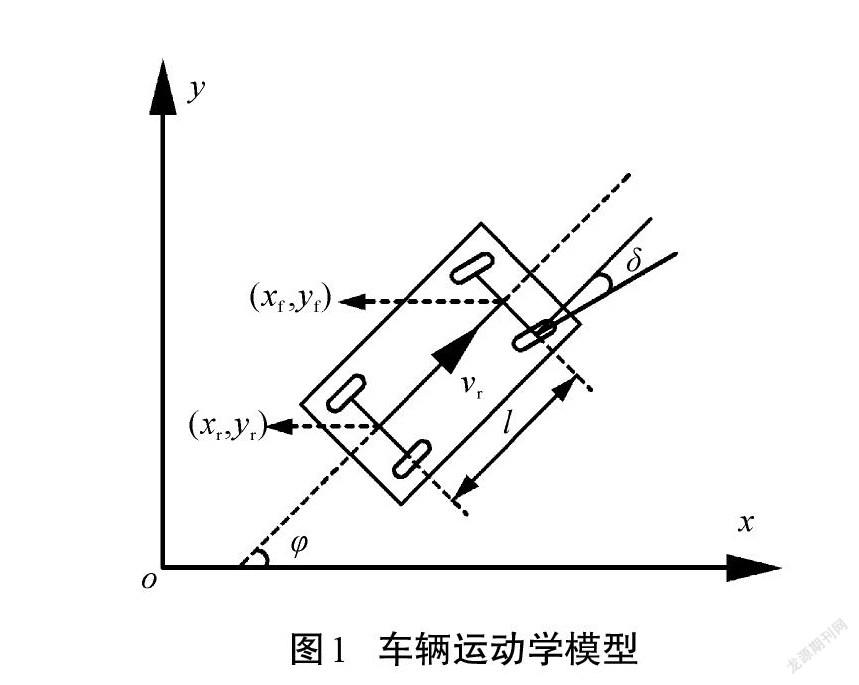
在泊车过程中，车辆速度一般不会大于10 km/h。假设车辆在行使过程中车轮不会发生侧向滑动，没有产生侧向力，车辆的侧向速度为0，车轮的侧偏角为0°[8]。因此，基于阿克曼转向原理对汽车运动模型进行简化，建立车辆运动学模型[9-12]。本文针对低速的泊车场合，基于阿克曼转向原理建立的车辆运动学模型如图1所示。

设[xf， yf]为车辆前轴中点坐标，[xr， yr]为后轴中点坐标，[φ]为车身横摆角，[φ]为横摆角速度，[χ]和[y]为惯性坐标系下车辆在x轴和y轴的速度，[l]为车辆的轴距，取后轴中心点速度[νr]为整车速度[ν]，[δ]为车辆的前轮转角。车辆的运动学方程可表示为：

[χ=νcosφ   y=νsinφ    φ=νtan（δ/l）⇒χyφ=νcosφνsinφνtan（δ/l）=f1f2f3] .    （1）

2    平行泊车参考路径

2.1   参考路径设计

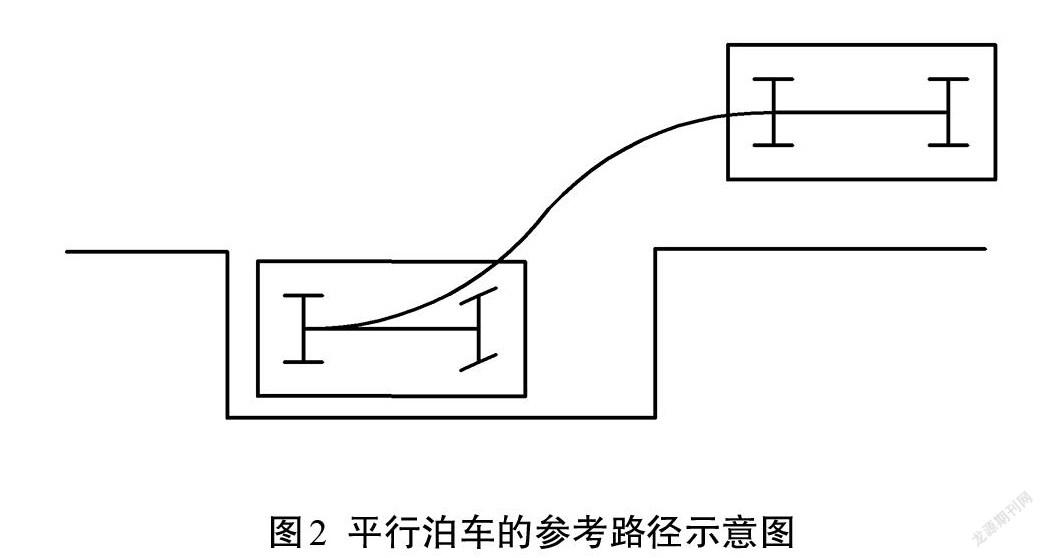
依据现实生活中的平行泊车情况，初步规划出平行泊车的参考路径示意图如图2所示。

通过图2可以看出，平行泊车轨迹中间的曲率变化率较大，而利用两段三阶贝塞尔曲线可以拟合曲率变化较大的曲线，因此，本文采用两段三阶贝塞尔曲线来规划出平行泊车的参考轨迹。

假设[A]、[B]、[C]和[D]是曲线[AD]的贝塞尔曲线控制点，那么以[u]为参数变量的三阶贝塞尔曲线方程可以表达如下：

[Q（u）=A（1-u）3+3B（1-u）2u+]

[3C（1-u）u2+Du3] .                    （2）

贝塞尔曲线[13]具有以下特性：

1）在贝塞尔曲线中，只有起点和终点在曲线上，其他点均为调整曲线形状和结束的控制点;

2）贝塞尔曲线通过起始点和终止点，并与起始点和终止点的折线相切，在对泊车路径进行规划时，可根据曲线的起始点和终止点的切线方向确定泊车起始点姿态和目标点姿态;

3）至少需要三阶贝塞尔曲线才能生成曲率连续的路径，三阶贝塞尔曲线均由2个端点和2个柄点共4个控制点进行控制，其中每个控制点的改变，均会影响这段曲线的所有部分[14]。

2.2   控制点的选择

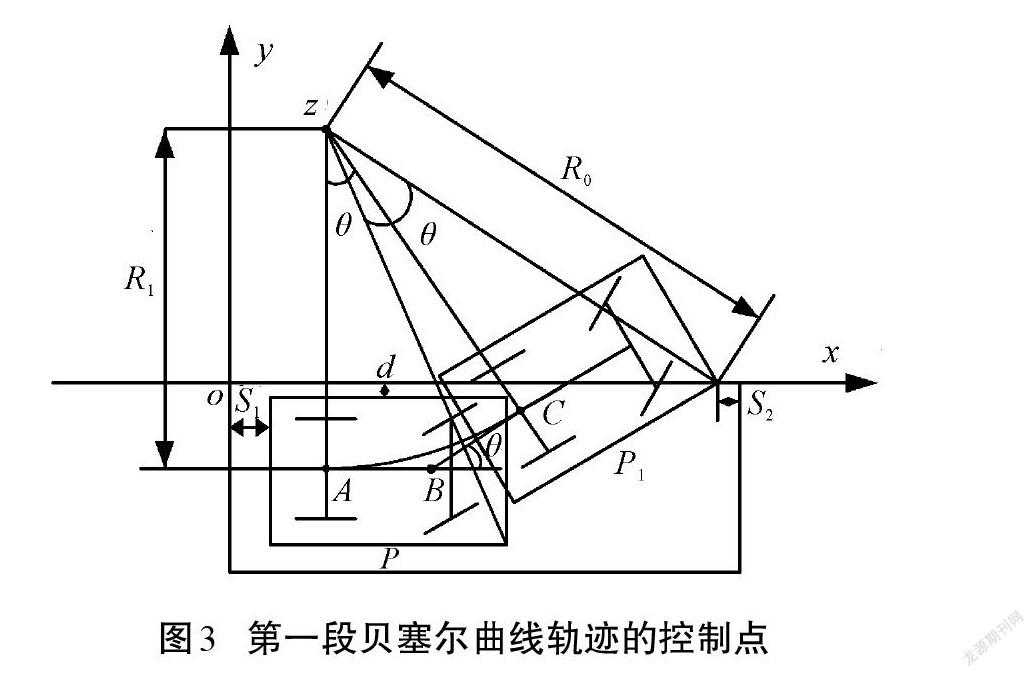
根据贝塞尔曲线的特性并联系实际平行泊车情况，利用倒推法（安全停放在车位里的车辆驶离车位进入道路）确定平行泊车参考轨迹贝塞尔曲线的控制点坐标。忽略后视镜的影响把车辆看作一个长方形，首先寻找第一段贝塞尔曲线轨迹的控制点，如圖3所示。车辆在停车位时，车尾与泊车位的后边线存在一段安全距离，记为[S1]，与旁边边界存在一段安全距离，记为[d]。根据车辆结构和环境条件的约束，车辆驶离停车位时车头右前端要与泊车位前角保持一段安全距离，记为[S2]，这样才能保证车辆的泊车安全。

假设车辆后悬的长度为[Lf] ，车身宽度为[W]，则第一段贝塞尔曲线轨迹的第一个控制点[A]的坐 标为：

[A（x， y）={S1+Lf，-W2-d}] .         （3）

根据阿克曼转向原理可知，车辆的转向中心点位于车辆后轴的延长线上，泊车过程中车辆处于位置[P]的后轴延长线与车辆处于位置[P1]的后轴延长线相交于一点[Z]，即Z点为车辆的转向瞬心。车辆从位置[P]行驶至位置[P1]时，转过的角度为[θ]，如图3所示。设车辆在此参考位置的转向半径为[R1]，根据几何关系算出[θ]的值和第三个控制点[C]的坐标。

设停车位长度为[Lp]，车辆轴距为l，前悬长度为[Lb]，则[θ]的值为：

[θ=arctanLp-S1-S2-LfR1-0.5W-d-]

[arctanl+LbR1+0.5W] .                       （4）

控制点[C]的坐标为：

[Cx， y={S1+Lf+R1 sinθ，R11-cosθ -0.5W-d}] .  （5）

由于泊车结束时要保证车辆平行于泊车位，则第一个控制点[A]处的斜率应该为0。根据三阶贝塞尔曲线的性质（三阶贝塞尔曲线起点处的斜率由前2个控制点决定，终点处的斜率由后2个控制点决定），第二个控制点[B]应该和第一个控制点[A]处于同一水平线上，如图3所示。根据几何关系可以算出第二个控制点[B]的坐标为：

[Bx， y=Cx-Cy-Aytanθ，Ay].    （6）

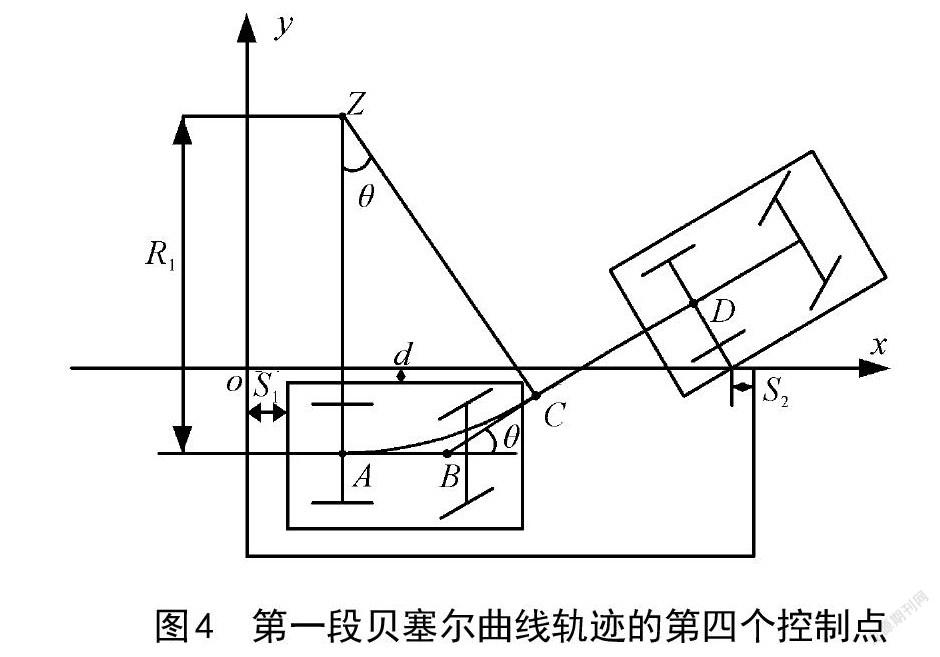
第一段贝塞尔曲线轨迹的第四个控制点如图4所示。为了保证车辆驶离泊车位进入道路时车尾不与泊车位前角发生碰撞，所以车辆继续向前行驶，直到车辆的后轴延长线与车身相交的点和泊车位的前角存在一段安全距离后，才能保证泊车的安全性，所以第四个控制点为车辆在此参考位置的后轴中心点[D]。

根据几何关系可计算出第四个控制点[D]的坐标为：

[Dx， y={C（x）+（l+Lb）cosθ，C（y）+（l+Lb）sinθ}].   （7）

至此，第一段贝塞尔曲线的4个点已经全部求出，需要调整方向驶入道路。根据贝塞尔曲线的性质（贝塞尔曲线通过起始点和终止点，并与起始点和终止点的折线相切），第二段贝塞尔曲线轨迹的起点[A1]必然经过第一段贝塞尔曲线的第四个点[D]，所以第二段贝塞尔曲线轨迹的起点[A1]为：

[A1x， y=Dx， y] .                   （8）

为了保证泊车轨迹的平顺，两段贝塞尔曲线的相交处斜率相同，所以第二段贝塞尔曲线轨迹的第二个控制点[B1]应在第一段贝塞尔曲线的控制点[BC]的延长线上。由于泊车的初始点车身摆正与车位平行，所以车辆要转过[θ]角度才能保证车身摆正，因此，车辆转过[θ]角度后的后轴中心为第二段贝塞尔曲线轨迹的第三个控制点[C1]。为了避免泊车起始就原地转向，在[C1]点前1 m处设置一个新的起点[D1]给车辆一个缓冲，则[D1]为第二段贝塞尔曲线轨迹的最后一个控制点。[C1D1]的延长线与[BC]的延长线交于一点，这个点为第二段贝塞尔曲线轨迹的第二个控制点[B1]。第二段贝塞尔曲线轨迹的控制点如图5所示。

[Z1]点为车辆的转向瞬心，[R2]为转向半径。根据几何关系可以求出第二段贝塞尔曲线轨迹的所有控制点的坐标。

[C1]的坐标为：

[C1x， y={A1（x）+R2 sinθ，A1（y）+R2（1-cosθ）}] ，    （9）

[D1]的坐标为：

[D1x， y={C1x+1，C1 y}] ，      （10）

[B1]的坐标为：

[B1x， y=A1x+C1y-A1ytanθ，D1y]. （11）

综上，两段三阶贝塞尔曲线规划出来的平行泊车参考轨迹的所有控制点的坐标表达式已经全部 求出。

2.3   生成參考轨迹

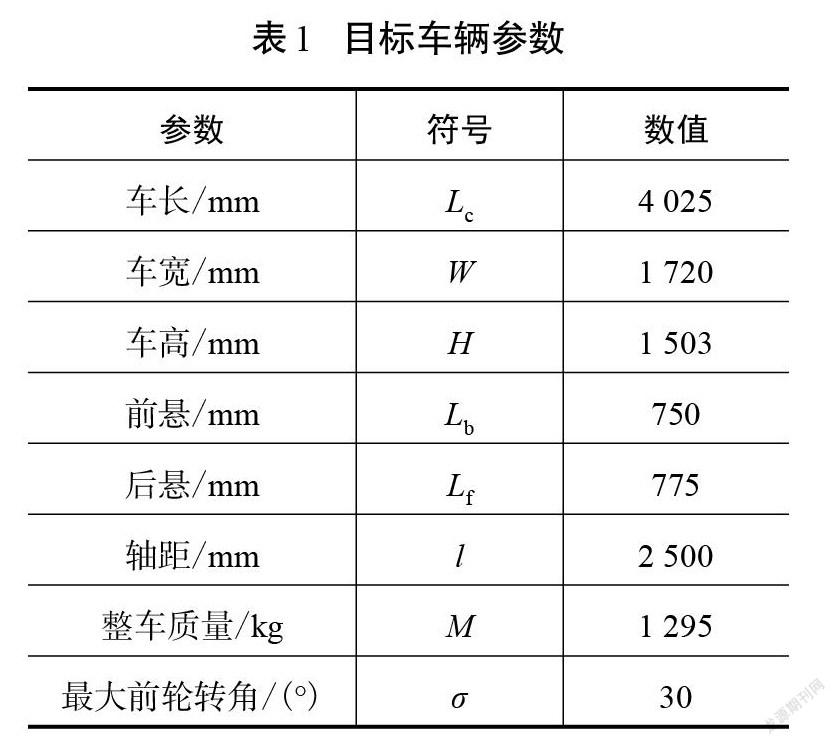
参考轨迹与车辆参数和泊车位参数有关。现选用某车型作为研究车辆，其参数如表1所示。

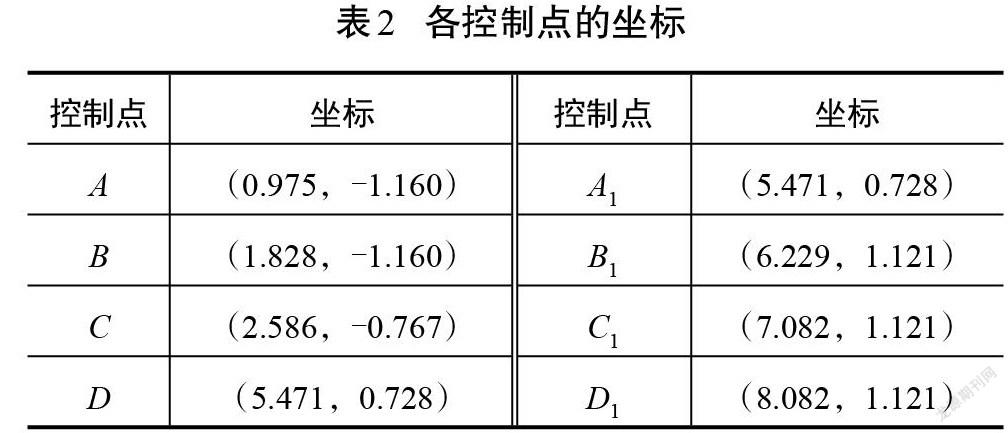
小型平行泊车位的标准尺寸为长6 m，宽2.5 m[15]。把目标车辆参数和泊车位参数代入平行泊车参考轨迹控制点的坐标表达式，求出所有控制点的坐标。各控制点的坐标如表2所示。

将表2中各控制点的坐标代入MATLAB的贝塞尔曲线程序，生成两段三阶贝塞尔曲线，即为平行泊车参考轨迹，如图6所示。

3    车辆泊车路径跟踪控制

运动控制作为平行泊车的重要组成部分，只有规划合适的泊车路径和合理的轨迹跟踪才能保证泊车成功。

模型预测控制是一种特殊的控制方法，是一种多变量控制策略，是通过描述系统动力学的系统模型来预测未来的状态和输出，然后根据目标函数计算系统的最优控制输入[16-18]。

3.1   模型

车辆运动学模型的运动方程为式（1）。

设选取的状态量为[χ=[x， y， φ]T]，选取的控制量为[u=[ν， δ]T]，对于参考轨迹的任意一个参考点用[r]表示，将式（1）改写成：

[χ=fχ， u⇒χr=f（χr， ur）] .         （12）

该车辆运动学模型非线性，需要将其线性化。基于运动高等数学中泰勒级数展开的思想将其线性化：

[χ=f（χr， ur）+∂f（χ， u）∂χ（χ-χr）+∂f（χ， u）∂uu-ur] . （13）

进行前向欧拉离散化得到：

[χ=χ-χry-yrφ-φr⇒χ=Mχ+Nu] ，         （14）

[M=∂f∂χ=00-νrsinφr00νrcosφr000]，            （15）

[N=∂f∂u=cosφrsinφrtanφr/l00νr/lcos2δr] .         （16）

此时获得了非线性运动模型。但基于MPC的原理，需要利用运动学模型进行递归运算，将连续的运动学模型转换成离散的运动学模型，利用数值分析中的前向欧拉离散化，得到：

[χk+1=TM+Eχk+TNuk=Mχk+Nuk].（17）

其中：[T]为采样时间，[E]为单位向量。

基于MPC控制理论，控制量需要用控制量差值来表示，因此，需进一步改进该模型，构建新的状态向量：

[ξk=χkuk-1] ，               （18）

[ξk+1=χk+1uk=Mξk+NΔuk] .  （19）

得到新的状态空间表达式，可以对该表达式进行改进，得到输出方程：

[ηk=ENx0χkuk-1=Gξk] .    （20）

3.2   预测

利用线性误差模型构建预测时域内的状态量误差输出量。

构建好线性误差模型后，利用该模型进行状态量误差预测。本文已经由[ξ（k）]预测出了[ξ（k+1）]，需预测未来[Np]个时刻的[ξ]，推导流程如下：

[ξ（k+1）=Mξ（k）+NΔuk，ξ（k+2）=M2ξ（k）+MNΔuk+NΔu（k+1），ξ（k+3）=M3ξ（k）+M2NΔu（k）+                    MNΔu（k+1）NΔu（k+2），              （21）                                      ⋮ξ（k+Np）=MNpξ（k）+MNp-1NΔu（k）+                MNp-2NΔu（k+1）+M0NΔu（k+Np-1）.]

[ηk+1=GMξk+GNuk，η（k+2）=GM2ξ（k）+GMNΔu（k）+                       GNΔu（k+1），η（k+3）=GM3ξ（k）+GM2NΔu（k）+                      GMNΔu（k+1）+GNΔu（k+2）， （22）                                      ⋮η（k+Np）=GMNpξ（k）+GMNp-1NΔu（k）+                         GMNp-2NΔu（k+1）+…+                         GM0NΔu（k+Np-1）.                  ]

[Np]为模型预测算法中的预测时域。综合上述推导，可以得到输出方程：

[Y=Ψξk+ΘΔU] .              （23）

其中：

[Y=ηk+1ηk+2⋮ηk+Np，Ψ=GMGM2⋮GMNp， ΔU=Δu（k）Δu（k+1）⋮Δu（k+Np-1），]

[Θ=GN0…0GMNGN…0?⋮⋮GMNp-1NGMNp-2N…GM0N] .

3.3   控制

构建目标函数和约束方程。

将目标表达式用二次型表示，得到目标函数：

[J=YTQQY+ΔUTRRΔU] .          （24）

其中：[Q]为输出权重矩阵，[R]为控制增量权重矩阵。在控制过程中希望只有控制量增量这一个自变量，因此，对表达式进行变换：

[I=Ψξk ，QQ=ENp⊗Q ，RR=ENp .]                        （25）

式中：[⊗]为克罗内克积。

得到目标函数：

[J=ΔUT（ΘTQQΘ+RR）ΔU+2ITQQΘΔU-]

[YrQQΘΔU+ITQQI+YrTQQY-2YrTQQI] .  （26）

MPC约束函数主要是针对控制量的增量以及控制量，由于本文控制的输入是控制量的增量，因此定义：

[ΔUmin≤ΔU≤ΔUmax] .             （27）

[Umin]和[Umax]分别为控制时域内控制量的最小值、最大值集合。

对于控制量的約束，需要进行公式递推，进而利用控制量增量来表达。已知某一时刻的控制量可以由上一时刻的控制量和这一时刻的控制量增量组成，即：

[uk=uk-1+Δuk+1，uk+1=uk-1+Δuk+Δuk+1，                                    ⋮                                                    （28）uk+Nc-1=uk-1+Δuk+      Δuk+1+…+Δuk+Nc-1.]

式中：[Nc]为控制时域。

将式（28）改写成：

[U=uk-1uk-1⋮uk-1+E000EE00⋮⋮⋮⋮EEEEΔukΔuk+1⋮Δuk+Nc-1] .  （29）

式（29）可简化为：

[U=Ut+M1ΔU] .               （30）

利用控制量的约束，将约束函数改写成控制量增量的形式：

[uminumin⋮umin≤ukuk+1⋮uk+Nc-1≤umaxumax⋮umax] .         （31）

式（31）可简化为：

[M1ΔU≤Umax-U ，-M1ΔU≤Umin-Ut .]               （32）

4    基于Carsim与Simulink的联合仿真试验

4.1    基于Carsim的仿真模型设置

试验车辆参数设置如图7所示。以Carsim数据库中的E-Class、 Sedan车作为原型进行建模，根据试验车的参数，在软件中设定好仿真车辆的整车质量、尺寸、轴距、转动惯量等主要参数，其他参数默认为数据库原型车的本来参数。

试验泊车位场景如图8所示。根据小型平行泊车位的标准尺寸（长6 m，宽2.5 m），搭建了3个平行泊车位。选择直线道路，路面摩擦系数为0.85。

4.2   联合仿真模型搭建

联合仿真模型如图9所示，主要由Carsim车辆模型、MPC追踪算法模型、停车制动模型、车辆前轮转角转换模型和车辆横、纵坐标转换模型     组成。

Carsim车辆模型：输入左、右前轮转角和制动主缸压力，输出车辆当前行驶状态的横、纵坐标和车辆横摆角。

MPC追踪算法模型：输入车辆当前行驶状态的横、纵坐标和车辆横摆角，输出前轮转角。

停车制动模型：当检测到车辆实际行驶状态的横坐标到达终止值时，给车辆发送制动信号使其 停车。

车辆前轮转角转换模型：由于Carsim模型使用角度制，而Simulink使用弧度制，需要进行数学转换。Simulink中MPC追踪模型输出的前轮转角是车辆模型的前轮转角，需要转换成Carsim模型中的前轮左、右转角。

车辆横纵坐标转换模型：由于Carsim模型的横、纵坐标是基于质心点，而Simulink中MPC追踪模型所使用的车辆横、纵坐标是基于后轴中心，因此，Carsim模型中输出车辆的横轴坐标和车辆横摆角时需要进行数学转换。

5    联合仿真试验结果分析

通过Simulink将联合仿真模型进行仿真，将得到的联合仿真泊车轨迹与参考轨迹进行对比分析，泊车轨迹与参考轨迹如图10所示，其中小图为轨迹的局部放大图。由图可以看出，泊车轨迹与参考轨迹基本吻合，说明设计的MPC模型的跟踪效果较为良好。

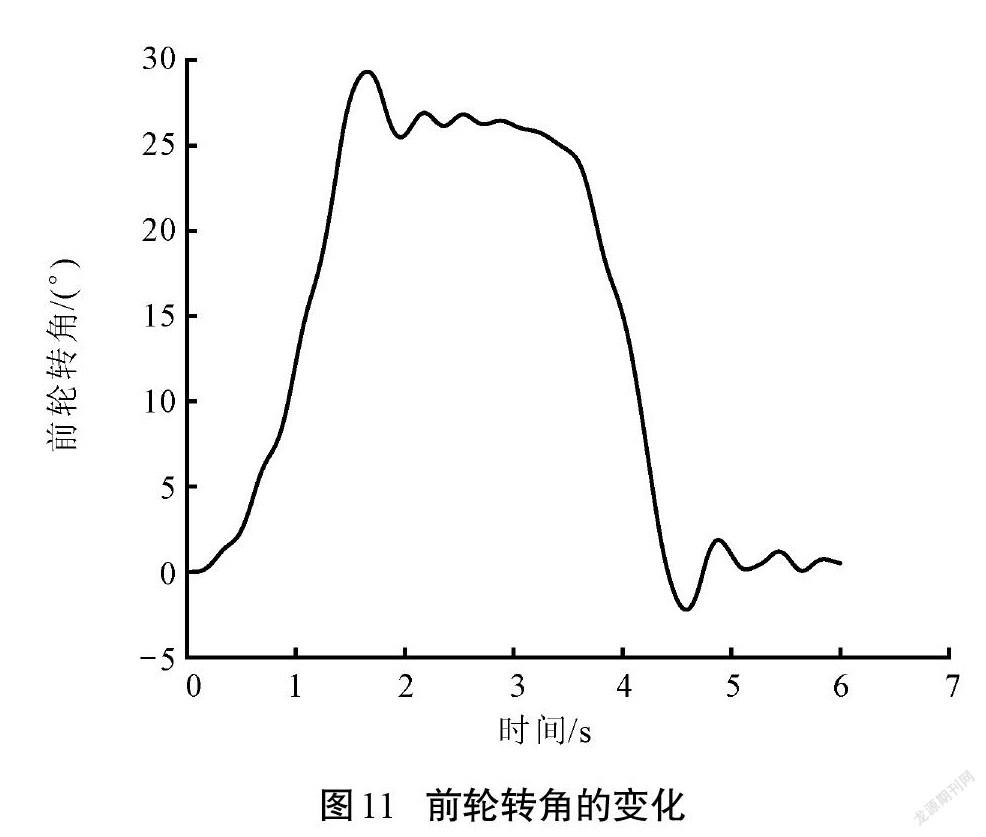
通过Simulink运行联合仿真模型，得到泊车过程中前轮转角的变化如图11所示。可以看出，车辆的车轮转角最大值约为29°，小于允许的最大值30°;泊车过程中前轮转角的变化是连续的，而且比较平缓。

通过Carsim软件运行联合仿真模型后，在Carsim中搭建的试验车泊车位场景中观察车辆的运行状态，车辆泊车轨迹跟踪如图12所示。图12（a）为车辆在泊车起始位置的状态，此时车辆与车位平行且与车位保持一定的安全距离;图12（b）为车辆泊车过程中车辆后轮即将进入泊车位的状态，此时车辆后轮与车位的右前角保持一定的安全距离，没有造成压角;图12（c）为车辆泊车过程中车辆前轮即将进入泊车位的状态，此时车辆前轮与车位的右前角保持一定的安全距离，没有造成压角;图12（d）与图12（e）为车辆泊车结束的状态，可以看出车辆与泊车位四周的画线都保持一定的安全距离;图12（f）为平行泊车全过程的状态，可以看出车辆安全进入了泊车位，成功地进行了泊车操作。

由此可知，本试验所规划的泊车参考轨迹能满足该试验车的安全泊车要求，所设计的轨迹跟踪方法能使该试验车具有良好的跟踪轨迹，在此条件下，该试验车能安全地完成泊车操作。

6    结论

利用两段三阶贝塞尔曲线规划泊车参考轨迹可解决轨迹曲率不连续的问题，可以得到比较平滑的泊车轨迹。根据车辆参数与车位参数计算出控制点，生成合适该参数的泊车轨迹，通过仿真验证了该轨迹规划方式在平行泊车中的可行性。针对轨迹跟踪的复杂性，选用模型预测控制跟踪算法，将运动学模型线性化、离散化，构建新状态向量，得到线性误差模型;利用线性误差模型构建预测时域内的状态量误差输出量，构建目标函数和约束方程;最后通过仿真验证了该算法在平行泊车轨迹跟踪方面的可行性。

参考文献

[1]     KIM D，CHUNG W，PARK S.Practical motion planning for car-parking control in narrow environment[J].IET Control Theory and Applications，2010，4（1）：129-139.

[2]     GÓMEZ-BRAVO F，CUESTA F，OLLERO A. Parallel and diagonal parking in nonholonomic autonomous vehicles[J].Engineering Applications of Artificial Intelligence，2001，14（4）：419-434.

[3]     DEMIRLI K，KHOSHNEJAD M.Autonomous parallel parking of a car-like mobile robot by a neuro-fuzzy sensor-based controller[J].Fuzzy Sets and Systems，2009，160（19）：2876-2891.

[4]     吳中伟.乘用车自动泊车系统路径规划与仿真分析[D].广州：华南理工大学，2018.

[5]     叶茂.基于B样条的多段式平行泊车轨迹规划研究[D].西安：长安大学，2020.

[6]     李红，王文军，李克强.基于B样条理论的平行泊车路径规划[J].中国公路学报，2016，29（9）：143-151.

[7]     MOON J，BAE I，CHA J G，et al. A trajectory planning method based on forward path generation and backward tracking algorithm for automatic parking systems[C]//17th IEEE International Conference on Intelligent Transportation Systems. IEEE，2014：719-724.

[8]     李臣旭，马世典，江绍康，等.基于CarSim与Matlab的泊车路径跟踪控制模型设计[J].汽车实用技术，2019（14）：47-49.

[9]     张驰.基于连续曲率的平行泊车路径规划研究[D].合肥：合肥工业大学，2015.

[10]   王国栋，张华强，苏庆华.基于运动学模型的轨迹跟踪方法研究[J].科技创新与应用，2021，11（25）：109-110，113.

[11]   谭光兴，符丹丹，丁颖，等.基于扩展卡尔曼滤波的汽车行驶状态估计[J].广西科技大学学报，2020，31（1）：18-24，44.

[12]   王鹏，陶小松，陈乐，等.低速四轮毂电动汽车电子差速控制仿真[J].广西科技大学学报，2019，30（2）：46-52，78.

[13]   ARASTEH S T，KALISZ A.Conversion between cubic bezier curves and catmull-rom splines[J].SN Computer Science，2021，2（5）：398.

[14]   刘学问，陶钧，徐海巍.基于三阶贝塞尔曲线的AGV轨迹规划研究[J].工业控制计算机，2018，31（1）：113-114.

[15]   李娅，祖永昶，司宇琪，等. 公安行业标准《城市道路路内停车位设置规范》（GA/T 850—2021）解析[J]. 中国标准化，2021（19）：186-191.

[16]   刘楠.基于MPC的无人驾驶车辆轨迹跟踪控制研究[D].西安：西安理工大学，2021.

[17]   辛鹏.自动驾驶车辆的路径跟踪模型预测控制方法研究[D].兰州：兰州理工大学，2021.

[18]   李威.模型预测控制在轨迹规划和车辆控制中的应用研究[D].杭州：浙江大学，2021.

Parallel parking path planning and tracking control

simulation analysis

QIN Liren， ZHANG Chengtao*， YANG Hang， ZHAO Zhedong， TAN Zedan

（School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology，

Liuzhou 545616， China）

Abstract： Parking safety has become a hot topic of current research as the inexperienced drivers cannot complete parallel parking operation in complicated parking environment with the increase of the number of cars. This paper studies and analyzes the path planning and path tracking of parallel parking based on the parameters of a certain vehicle model. Firstly， a collision-free reference path is drawn based on vehicle kinematics with two third-order Bezier curves and backward inference method. Then the path tracking is carried out by using model predictive control. Finally， Simulink and Carsim          co-simulation are conducted. The results show the obtained trajectory curvature is continuous and safe without collision. The trajectory tracking result is consistent with the reference trajectory， which verifies the feasibility of the proposed method for parallel parking path planning and tracking control.

Key words： parallel parking; path planning; path tracking; Bezier curve; model prediction control

（責任编辑：黎  娅）